一、定義

　數(shù)學(xué)中，如果一個函數(shù)足夠平滑的話，已知函數(shù)在某一點(diǎn)的各階導(dǎo)數(shù)值的情況之下，泰勒公式可以用這些導(dǎo)數(shù)值做系數(shù)構(gòu)建一個多項式來近似函數(shù)在這一點(diǎn)的鄰域中的值。泰勒公式還給出了這個多項式和實(shí)際的函數(shù)值之間的偏差。

　泰勒公式是將一個在x=x₀處具有n階導(dǎo)數(shù)的函數(shù)f(x)利用關(guān)于(x-x₀)的n次多項式來逼近函數(shù)的方法。

　若函數(shù)f(x)在包含x₀的某個閉區(qū)間[a,b]上具有n階導(dǎo)數(shù)，且在開區(qū)間(a,b)上具有(n+1)階導(dǎo)數(shù)，則對閉區(qū)間[a,b]上任意一點(diǎn)x，成立下式：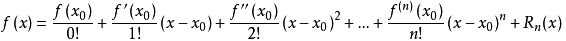

　等號后的多項式稱為函數(shù)f(x)在x₀處的泰勒展開式，剩余的R_n(x)是泰勒公式的余項

　麥克勞林展開

　　函數(shù)的麥克勞林展開指上面泰勒公式中x₀取0的情況，即是泰勒公式的特殊形式，若f(x)在x=0處n階連續(xù)可導(dǎo)，則下式成立：

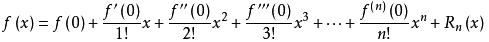
　其中f⁽ⁿ⁾(x)表示f(x)的n階導(dǎo)數(shù)，實(shí)際應(yīng)用中，泰勒公式需要截斷，只取有限項，一個函數(shù)的有限項的泰勒級數(shù)叫做泰勒展開式。泰勒公式的余項可以用于估算這種近似的誤差。

二、利用泰勒公式對e^x展開

　運(yùn)用麥克勞林展開式并舍棄余項：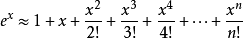

　當(dāng)x=1時：

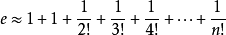
三、形象化解釋（參考其他博客）

　想象一個函數(shù)，你只能觀測其中很小一段的圖像，現(xiàn)在需要從這一小段預(yù)測其他點(diǎn)的函數(shù)值：

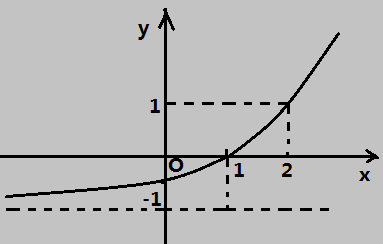
　假設(shè)泰勒原點(diǎn)在x=0，即你只能觀測x=0附近很小一段的函數(shù)圖像

　這時你可能會想，切線在這段符合得挺好，就用它估計吧，這條線的斜率就是f'(0)：

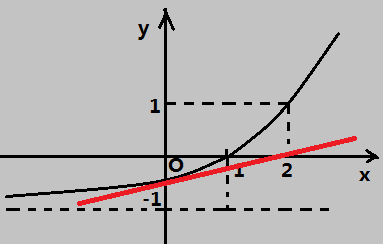
　結(jié)果和實(shí)際相去甚遠(yuǎn)

　你可能會很奇怪，為什么看起來這么接近，結(jié)果還差這么大，就使勁盯著這段函數(shù)看啊看：

　盯了半天，經(jīng)過了n次放大，你終于發(fā)現(xiàn)曲線的左右比切線都要高一些，像是一條拋物線。于是你在切線的基礎(chǔ)上加了一個拋物線因子，對應(yīng)的二次斜率就是f''(0)/2：

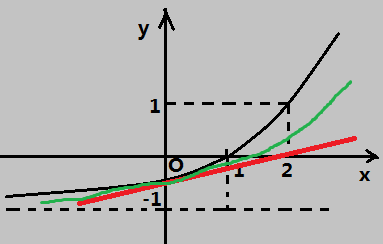
　雖然還是很不準(zhǔn)，還是比一開始的預(yù)測準(zhǔn)了不少，于是你信心大增，很快發(fā)現(xiàn)了新的不同，利用三次曲線去預(yù)測：

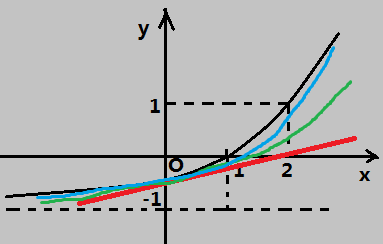
 　然后你會發(fā)現(xiàn)越來越準(zhǔn)，直到預(yù)測了n次，你看得累了，預(yù)測結(jié)果和真實(shí)函數(shù)也差不多了，就把可能的最大偏差用一個余項表示，當(dāng)然離原點(diǎn)越遠(yuǎn)就越不準(zhǔn)，這個余項也和x有關(guān)。泰勒公式可以說是用函數(shù)在某一點(diǎn)的導(dǎo)數(shù)逐次逼近函數(shù)的過程。