一、背景介紹

　假設我們的訓練集每個樣本都有兩個特征-$x_1, x_2$，也就是下面的$i_1, i_2$，每個樣本的標簽為$o_1, o_2$（假設標簽是二分類，我們用one-hot表示標簽）

　我們要用下面的神經網絡來進行訓練：

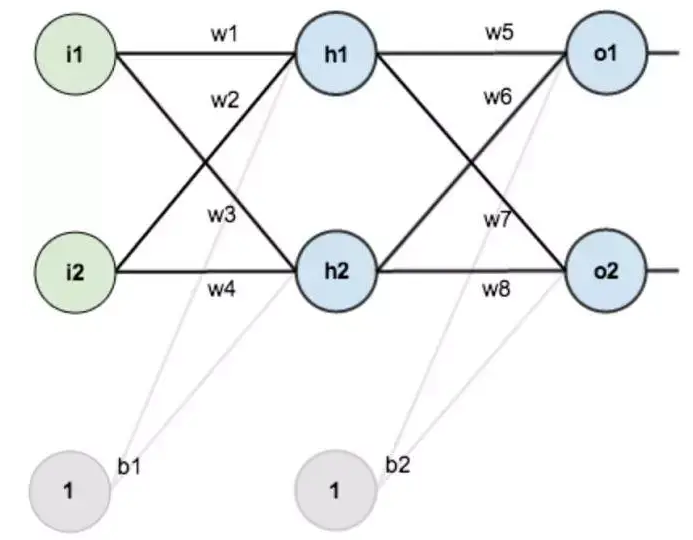
二、前向傳播與反向傳播

　現在對他們賦上初值，如下圖：（你暫時可以認為下面的$o_1=0.01, o_2=0.99$就是我們的標簽，真實標簽也許應該是$[0, 1]$）

 

 

 

　1）前向傳播

　　輸入層到隱藏層

 $net_{h2} = w_3 * i_1 + w_4*i_2 + b_1 * 1$

$net_{h2} = 0.25 * 0.05 + 0.3 * 0.1 + 0.35 * 1 = 0.3925$

$out_{h_2} = 0.5968$

　　隱藏層---->輸出層：

 

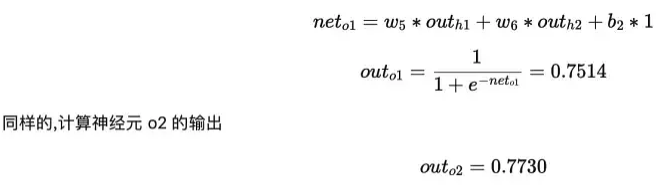
 $net_{o1} = 0.4 * 0.5932 + 0.45 * 0.5968 + 0.6 * 1 = 1.1058$

$out_{o1} = 0.7514$

 

$net_{o2} = w_7 * out_{h1} + w_8 * out_{h2} + b_2 * 1$

$net_{o2} = 0.5 * 0.5932 + 0.55 * 0.5968 + 0.6 * 1 = 1.2248$

$out_{o2} = 0.7730$

　　有了輸出，我們的輸出和真實值之間的差距是多少呢？

 

　2）反向傳播

　　計算總誤差

 這就是我們當前正向傳播后的loss

 

　　隱藏層到輸出層的權重更新

　　我們先以更新權重$w_5$為例，下面的圖可以更直觀的看清楚誤差是怎樣反向傳播的

 

 

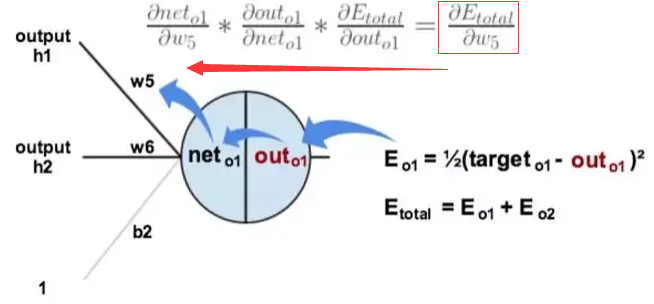
　　我們分別計算每個式子的值：

　　最后三者相乘：

 

 

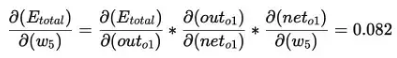
　　看看上面的公式,我們發現：

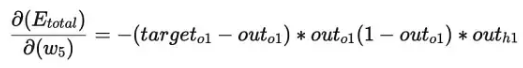
 $\frac{\partial\left(E_{\text {total}}\right)}{\partial\left(w_{5}\right)}=-\left(\operatorname{target}_{o 1}-\text {out}_{o 1}\right) * \text { out }_{o 1}\left(1-\text {out}_{o 1}\right) * out_{h1}=0.7414 * 0.1868 * 0.5932 = 0.0821$

 

$\frac{\partial\left(E_{\text {total}}\right)}{\partial\left(w_{6}\right)}=-\left(\operatorname{target}_{o 1}-\text {out}_{o 1}\right) * \text { out }_{o 1}\left(1-\text {out}_{o 1}\right) * out_{h2}=0.7414 * 0.1868 * 0.5968 = 0.0827$

 

$\frac{\partial\left(E_{\text {total}}\right)}{\partial\left(w_{7}\right)}=-\left(\operatorname{target}_{o 2}-\text {out}_{o 2}\right) * \text { out }_{o 2}\left(1-\text {out}_{o 2}\right) * out_{h1}=-0.217 * 0.1755 * 0.5932 = -0.0226$

 

$\frac{\partial\left(E_{\text {total}}\right)}{\partial\left(w_{8}\right)}=-\left(\operatorname{target}_{o 2}-\text {out}_{o 2}\right) * \text { out }_{o 2}\left(1-\text {out}_{o 2}\right) * out_{h2}=-0.217 * 0.1755 * 0.5968 = -0.0227$

 

　　有了梯度，可以用來更新$w_5$了：這里學習率設置為0.5

　　輸入層到隱藏層的權值更新

 

 

 

　　所以我們要對$w_1$更新的話，$w_1$參與了$net_{h1}$的計算，$net_{h1}$參與了$out_{h1}$的計算，$out_{h1}$參與了$net_{o1}$和$net_{o2}$的計算，$net_{o1}$和$net_{o2}$參與了$out_{o1}$和$out_{o2}$的計算，$out_{o1}$和$out_{o2}$參與$E_{total}$的計算，我們來逐個剖析

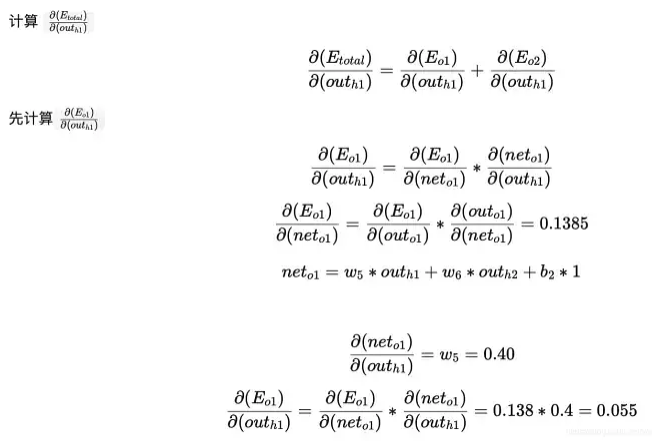
　　同理，計算出

 

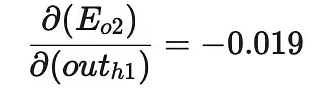
　　兩者相加,得到總值

 

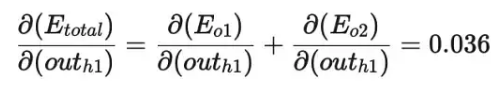
　　最后，三者相乘

 

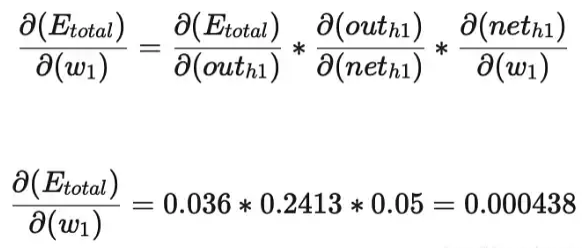
　　這樣誤差反向傳播法就完成了，最后我們再把更新的權值重新計算，不停地迭代。

 

三、參考

　本文參考這里，感謝作者的分享！