定義：

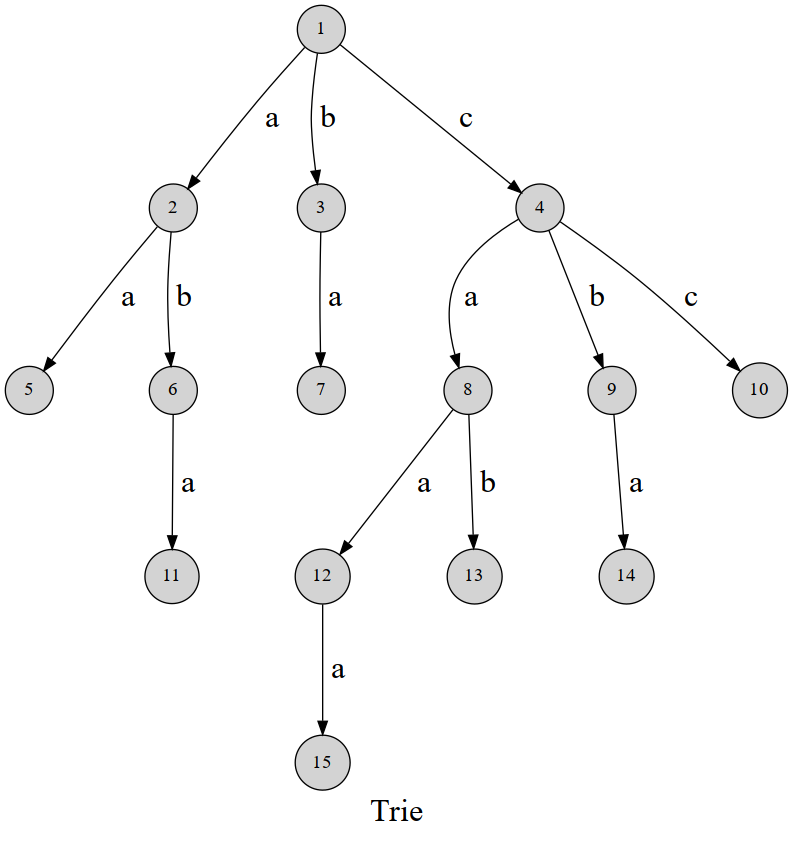
將多個字符串以樹的方式存儲即為字典樹，如圖，\(1,4,3,12\) 表示 \(cca\) ，我么用 \(ch[i][j]\) 來表示第 \(i\) 個節點的 \(j\) 字符所指向的下一個節點，\(tag[u]\) 表示節點 \(u\) 是否代表一個字符串的結尾，如果是的話，\(tag[u]=1\)。

模板CODE

添加字符串

//n表示即將要向字典樹插入n個字符串
const N 100005;
scanf("%d",&n);
    for (int i=1;i<=n;i++){
        char s[N];
        scanf("%s",s+1);
        int u=1;
        for (int j=1;s[j];j++){
            int c=s[j]-'a';
            if (!ch[u][c]) ch[u][c]=++tot;
            u=ch[u][c];
        }
        tag[u]=1;
    }

字符串查找

//查看字符串s是否在字典樹當中，如果在輸出OK，否則輸出WRONG
char s[N];
scanf("%s",s+1);
        int u=1;
        for (int i=1;s[i];i++){
            int c=s[i]-'a';
            u=ch[u][c];
            if (!u) break;
        }
        if (tag[u]==1){
            puts("OK");
            continue;
        }
        else {
            puts("WRONG");
            continue;
        }

例題

P2580 于是他錯誤的點名開始了
例題代碼：

#include<cstdio>
using namespace std;
const int N=500010;

int n,m;
int ch[N][30];
int tag[N];
int tot=0;
char s[N];

int main(){
    freopen("test_point/input.in","r",stdin);
    scanf("%d",&n);
    for (int i=1;i<=n;i++){
        scanf("%s",s+1);
        int u=1;
        for (int j=1;s[j];j++){
            int c=s[j]-'a';
            if (!ch[u][c]) ch[u][c]=++tot;
            u=ch[u][c];
        }
        tag[u]=1;
    }
    scanf("%d",&m);
    while (m--){
        scanf("%s",s+1);
        int u=1;
        for (int i=1;s[i];i++){
            int c=s[i]-'a';
            u=ch[u][c];
            if (!u) break;
        }
        if (tag[u]==2){
            puts("REPEAT");
            continue;
        }
        else if (tag[u]==1){
            puts("OK");
            tag[u]=2;
            continue;
        }
        else {
            puts("WRONG");
            continue;
        }
    }
    return 0;
}

維護異或極值

01-trie：01-trie 是指字符集為 {0,1} 的 trie。01-trie 可以用來維護一些數字的異或和，支持修改（刪除 + 重新插入），和全局加一
維護異或路徑：此類問題會給定一棵樹，讓你求出這棵樹最長的異或路徑，對于此類問題，我們需要先明白異或運算的性質
模板題目: https://www.luogu.com.cn/problem/P4551

• 交換律: \(a \oplus b=b \oplus a\)
• 結合律：\((a \oplus b) \oplus c=a \oplus (b \oplus c)\)
• 自反性：\(a \oplus a=0\)
• 與 \(0\) 異或：\(a \oplus 0=a\)

根據以上性質我們可以得到一個推論：\(a \oplus b \oplus b=a \oplus (b \oplus b)=a \oplus 0=a\) ，因此，在樹或圖中，如果定義一條路徑的異或值為路徑上所有邊權的異或和，那么：
從節點 \(u\) 到節點 \(v\) 的路徑異或值等于從根節點到 \(u\) 的異或值 \(xor[u]\) 與從根節點到 \(v\) 的異或值 \(xor[v]\) 的異或，因此我們可以預處理所有節點到根節點的異或路徑，存在 \(xor[]\) 數組中，然后對 \(xor[]\) 數組構造字典樹，如下圖
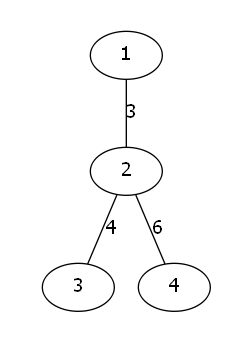$\longrightarrow $
接著，我們存好后，用兩個指針在字典樹上遍歷，對于每次，對要盡可能選擇不一樣的兩位，這樣可以保證異或值最大，因為高位的 \(1\) 比他下面所有位的 \(1\) 加起來都大，但是如果存在兩種選擇都可以讓該為異或為 \(1\) ，則需要dfs一下
模板CODE：

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;

const int N=100005;
int n;
int tr[2000000][2];
struct edge{
    int v;
    int w;
};
vector<edge> g[N];
int xr[N];
int cnt=1;
int h;
int res,ans;

void dfs(int u,int fa){
    for (edge ed:g[u]){
        int v=ed.v,w=ed.w;
        if (v==fa) continue;
        xr[v]=xr[u]^w;
        dfs(v,u);
    }
    return ;
}

void dfs1(int i,int j,int k){
    if (!k){
        ans=max(ans,res);
        return ;
    }
    if ((tr[i][0]&&tr[j][1])||(tr[i][1]&&tr[j][0])){
        if (tr[i][0]&&tr[j][1]){
            res+=(1<<(k-1));
            dfs1(tr[i][0],tr[j][1],k-1);
            res-=(1<<(k-1));
        }
        if (tr[i][1]&&tr[j][0]){
            res+=(1<<(k-1));
            dfs1(tr[i][1],tr[j][0],k-1);
            res-=(1<<(k-1));
        }
    }
    else{
        if (tr[i][0]&&tr[j][0]) dfs1(tr[i][0],tr[j][0],k-1);
        else if (tr[i][1]&&tr[j][1]) dfs1(tr[i][1],tr[j][1],k-1);
    }
}

int main(){
    scanf("%d",&n);
    for (int i=1;i<=n-1;i++){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        g[u].push_back((edge){v,w});
        g[v].push_back((edge){u,w});
    }
    dfs(1,-1);
    int maxn=0;
    for (int i=1;i<=n;i++) maxn=max(maxn,xr[i]);
    while (maxn) maxn>>=1,h++;
    if (h==0) h++;
    for (int i=1;i<=n;i++){
        int u=1;
        for (int j=h-1;j>=0;j--){
            int w=(xr[i]>>j)&1;
            if (!tr[u][w]) tr[u][w]=++cnt;
            u=tr[u][w];
        }
    }
    dfs1(1,1,h);
    printf("%d",ans);
    return 0;
}