到底什么是AI框架？AI框架有什么用？

最近一個月朋友老來挑戰我：“什么才是AI框架？”，于是趁著夜深人靜的時候，真正地去梳理什么是AI框架，下面是我對AI框架的一些思考。

到底什么是AI算法？什么是神經網絡？神經網絡有什么用？為什么神經網絡需要訓練？什么是模型？AI框架有什么用？AI框架能解決什么問題？

上面的幾個問題其實還挺有挑戰的。下面我們來對清楚一些基本概念：深度學習是機器學習研究領域中的一種，深度學習的概念源于對人工神經網絡的研究，很多深度學習算法都使用神經網絡進行表示，因為神經網絡的性能精度和通用效果都非常好，于是業界習慣性地把深度學習算法等同于AI。

深度學習范式主要是通過發現經驗數據中，錯綜復雜的結構進行學習。通過構建包含多個處理層的計算模型（網絡模型），深度學習可以創建多個級別的抽象層來表示數據。例如，卷積神經網絡CNN可以使用大量圖像進行訓練，例如對貓狗分類去學習貓和狗圖片的特征。這種類型的神經網絡通常從所采集圖像中，包含的像素進行學習。

本章將從深度學習的原理開始，進而深入地討論在實現深度學習的計算過程中使用到的AI框架，看看AI框架具體的作用和目的。

深度學習原理

深度學習的概念源于人工神經網絡的研究，但是并不完全等于傳統神經網絡。在叫法上，很多深度學習算法中都會包含”神經網絡”這個詞，比如：卷積神經網絡、循環神經網絡。所以，深度學習可以說是在傳統神經網絡基礎上的升級，約等于神經網絡。

雖然深度學習理論最初創立于上世紀八十年代，但有兩個主要原因導致其直到近年來才得以發揮巨大作用：

• 深度學習需要大量的標簽化數據。例如，無人駕駛汽車模型訓練需要數萬億張圖片和數千萬小時的視頻進行學習。
• 深度學習需要巨大的計算能力。例如，需要局別并行架構和集群組網能力的高性能 GPU/NPU 對于深度學習計算進行加速。

神經網絡

現在業界比較通用對神經網絡概念的解釋是：

1. 從通用概念的角度上來看的話，神經網絡是在模擬人腦的工作機制，神經元與神經突觸之間的連接產生不同的信號傳遞，每個神經元都記錄著信號的特征。
2. 從統計學的角度來說，就是在預測數據的分布，從數據中學得一個模型，然后再通過這個模型去預測新的數據（這一點就要求測試數據和訓練數據必須是同分布）。

實際上，一個神經網絡由多個神經元結構組成，每一層的神經元都擁有多個輸入和輸出，一層可以由多個神經元組成。例如，第2層神經網絡的神經元輸出是第3層神經元的輸入，輸入的數據通過神經元上的激活函數（非線性函數如tanh、sigmod等），來控制輸出的數值。

數學上簡單地理解，單個神經元其實就是一個 $X·W$ 的矩陣乘，然后加一個激活函數 $fun(X·W)$，通過復合函數組合神經元，就變成一個神經網絡的層。這種模擬生物神經元的數學計算，能夠很好地對大規模獨立同分布的數據進行非線性映射和處理，使得其能夠應對到人工智能的不同任務。

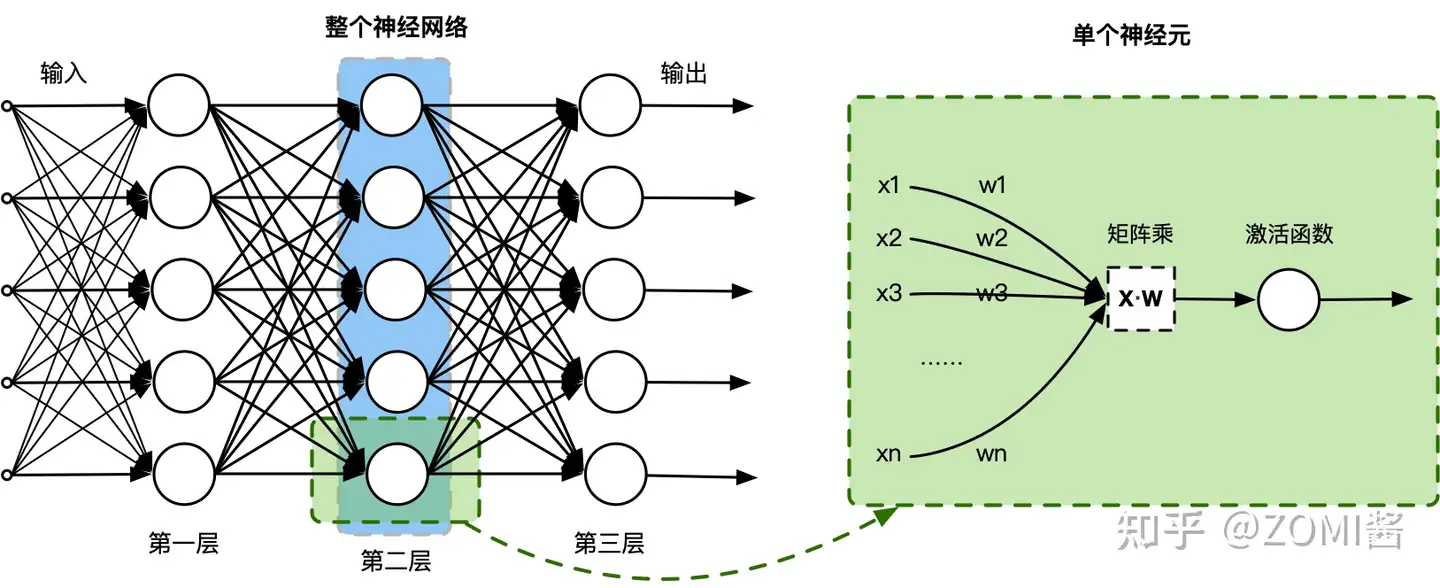
函數逼近

現在，如果把神經網絡看做一個復雜函數，那么這個函數可以逼近任何函數。上面只是定義了什么是神經網絡，其實神經網絡內部的參數（神經元鏈接間的權重）需要通過求解函數逼進來確定的。

直觀地看下一個簡單的例子：假設1個圓圈代表一個神經元，那么一個神經元可模擬“與或非”3種運算，3個神經元組成包含1個隱層的神經網絡即可以模擬異或運算。因此，理論上，如此組合的神經網絡可模擬任意組合的邏輯函數。

很多人會說神經網絡只要網絡模型足夠深和足夠寬，就可以擬合（fit）任意函數，這樣的說法數學理論上靠譜嗎？嚴格地說，神經網絡并不是擬合任意函數，其數學理論建立在通用逼近定理（Universal approximation theorem）的基礎之上：

神經網絡則是傳統的逼近論中的逼近函數的一種推廣。逼近理論證明，只要神經網絡規模經過巧妙的設計，使用非線性函數進行組合，它可以以任意精度逼近任意一個在閉集里的連續函數。

既然神經網絡模型理論上能夠逼近任何連續函數，那么有意思的事情就來了。我們可以利用神經網絡處理數學上分類、回歸、擬合、逼近等問題啦。例如在CV領域對人臉圖像進行分類、通過回歸檢測圖像中的車輛和行人，在NLP中對離散的語料數據進行擬合。

可是，神經網絡介紹現在還只能逼近任何函數，逼近函數需要求解，怎么去求解神經網絡呢？

函數逼近求解：在數學的理論研究和實際應用中經常遇到逼近求解問題，在選定的一類函數中尋找某個函數 $f$，使它與已知函數 $g$（或觀測數據）在一定意義下為最佳近似表示，并求出用 $f$ 近似表示 $g$ 而產生的最小誤差（即損失函數）：

loss(w)=f(w)?g :eqlabel:fund_02_eq1

所以，神經網絡可以通過求解損失函數的最小值，來確定這個神經網絡中的參數 $w$，從而固化這個逼近函數。

反向求導

深度學習一般流程是：1）構建神經網絡模型，2）定義損失函數和優化器（優化目標），3）開始訓練神經網絡模型（計算梯度并更新網絡模型中的權重參數），4）最后驗證精度，其流程如下圖所示，前三步最為重要。

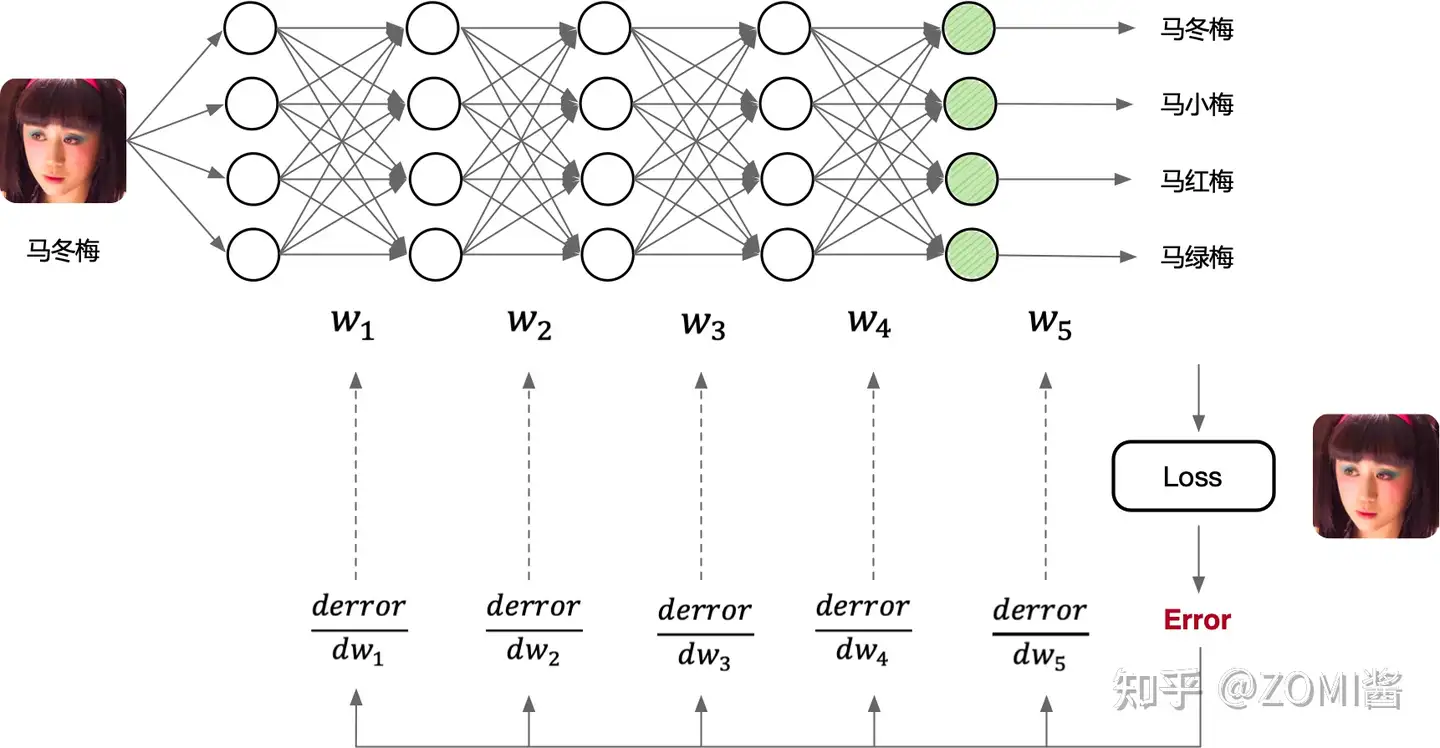
因為AI框架已經幫我們封裝好了許多功能，所以遇到神經網絡模型的精度不達標，算法工程師可以調整網絡模型結構、調節損失函數、優化器等參數重新訓練，不斷地測試驗證精度，因此很多人戲稱算法工程師又是“調參工程師”。

但是在這一過程中，這種機械的調參是無法觸碰到深度學習的本質的，為了了解實際的工作原理，進行總結：訓練的過程本質是進行反向求導（反向傳播算法實現）的過程，然后通過迭代計算求得神經網絡中的參數，調整參數是控制這一過程的前進速度和方向。

上面這段話我們仍然聽不懂，沒關系。我們需要了解的是，什么是訓練？訓練的作用是什么？為什么要求導？為什么在訓練的過程中用到求導？求導的數學依據和意義在哪里？

導數是函數的局部性質。一個函數在某一點的導數，描述該函數在這一點附近的變化率。如果函數的自變量和取值都是實數的話，函數在某一點的導數就是該函數所代表的曲線在這一點上的切線斜率。

那么，針對導數的幾何意義，其可以表示為函數在某點處的切線斜率；在代數上，其意味著可以求得函數的瞬時變化率。如果把神經網絡看做一個高維復雜的函數，那么訓練的過程就是對損失函數進行求導，利用導數的性質找到損失函數的變化趨勢，每次一點點地改變神經網絡仲的參數 $w$，最后逼近得到這個高維函數。

AI框架的作用

AI框架與微分關系

根據深度學習的原理，AI框架最核心和基礎的功能是自動求導（后續統一稱為自動微分，AutoGrad）。

接下來有個更加重要的問題，深度學習中的神經網絡為什么需要反向求導？

按照高中數學的基本概念，假設神經網絡是一個復合函數（高維函數），那么對這個復合函數求導，用的是鏈式法則。舉個簡單的例子，考慮函數 $z=f(x,y)$，其中 $x=g(t),t=h(t)$ ，其中 $g(t), h(t)$ 是可微函數，那么對函數 $z$ 關于 $t$ 求導，函數會順著鏈式向外逐層進行求導。

dxdt=?z?xdxdt+?z?ydydt :eqlabel:fund_02_eq2

既然有了鏈式求導法則，而神經網絡其實就是個龐大的復合函數，直接求導不就解決問題了嗎？反向到底起了什么作用？下面來看幾組公式。

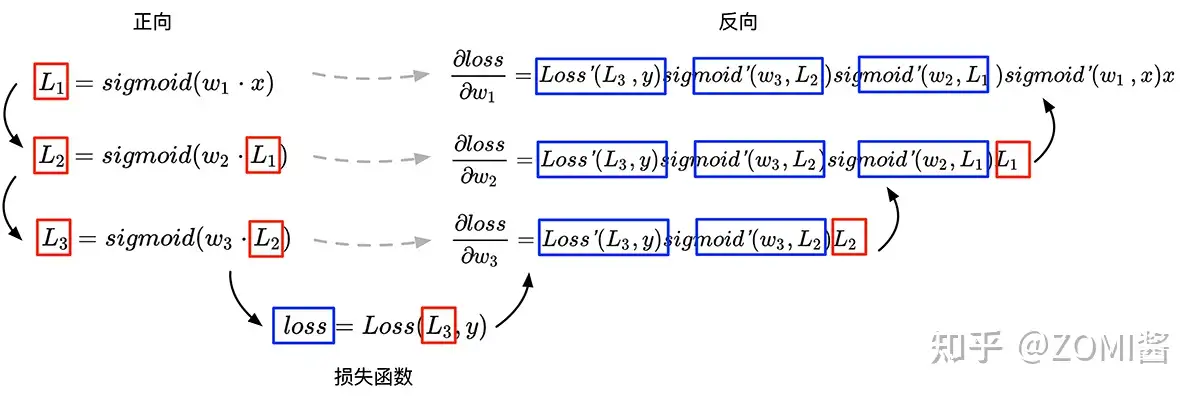
假設用3組復合函數來表示一個簡單的神經網絡：

L1=sigmoid(w1?x) :eqlabel:fund_02_eq3

L2=sigmoid(w2?L1) :eqlabel:fund_02_eq4

L3=sigmoid(w3?L2) :eqlabel:fund_02_eq5

現在定義深度學習中網絡模型的損失函數，即優化目標：

loss=Loss(L3,y) :eqlabel:fund_02_eq6

根據鏈式求導法則可以得到：

?loss?w3=Loss′(L3,y)sigmoid′(w3,L2)L2 :eqlabel:fund_02_eq7

?loss?w2=Loss′(L3,y)sigmoid′(w3,L2)sigmoid′(w2,L1)L1 :eqlabel:fund_02_eq8

?loss?w1=Loss′(L3,y)sigmoid′(w3,L2)sigmoid′(w2,L1)sigmoid′(w1,x)x :eqlabel:fund_02_eq9

假設神經網絡為上述公式 $L_1,L_2, L_3$，對損失函數求神經網絡中各參數求偏導，可以看到在接下來的求導公式中，每一次導數的計算都可以重用前一次的的計算結果，于是Paul Werbos在1975年發明了反向傳播算法（并在1990重新使用神經網絡對反向求導進行表示）。

這里的反向，指的是圖中的反向箭頭，每一次對損失函數中的參數進行求導，都會復用前一次的計算結果和與其對稱的原公式中的變量，更方便地對復合函數進行求導。

AI框架與程序結合

下面左圖的公式是神經網絡表示的復合函數表示，藍色框框表示的是AI框架，AI框架給開發者提供構建神經網絡模型的數學操作，AI框架把復雜的數學表達，轉換成計算機可識別的計算圖。

定義整個神經網絡最終的損失函數為 $Loss$ 之后，AI框架會自動對損失函數求導（即對神經網絡模型中各個參數求其偏導數）。

上面提到過，每一次求導都會復用前一次的計算結果和與其對稱的原公式中的變量。那么干脆直接基于表示神經網絡的計算圖計的基礎之上，構建一個與之對稱的計算圖（反向計算圖）。通過反向計算圖表示神經網絡模型中的偏導數，反向傳播則是對鏈式求導法則的展開。

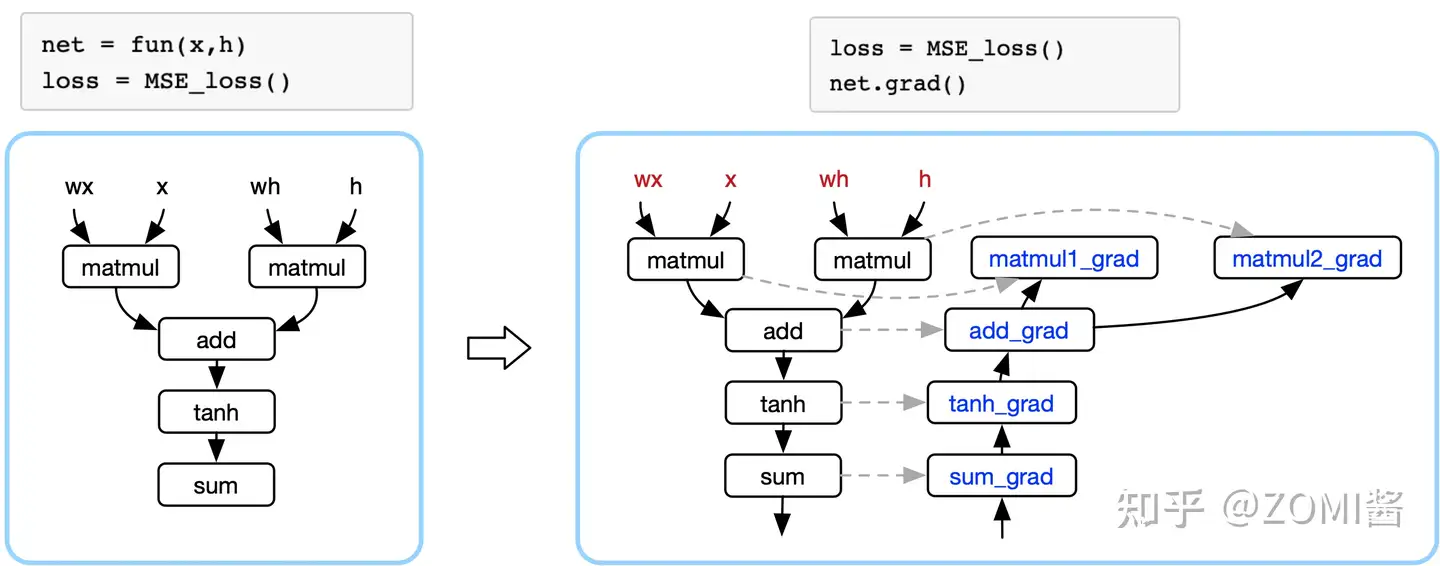
通過損失函數對神經網絡模型進行求導，訓練過程中更新網絡模型中的參數（函數逼近的過程），使得損失函數的值越來越小（表示網絡模型的表現越好）。這一過程，只要你定義好網絡AI框架都會主動地幫我們完成。

很有意思的是，AI框架對整體開發流程進行了封裝，好處是讓算法研究人員專注于神經網絡模型結構的設計（更好地設計出逼近復合函數），針對數據集提供更好的解決方案，研究讓訓練加速的優化器或者算法等。

綜上所述，AI框架最核心的作用是提供開發者構建神經網絡的接口（數學操作），自動對神經網絡訓練（進行反向求導，逼近地求解最優值），得到一個神經網絡模型（逼近函數）用于解決分類、回歸、擬合的問題，實現目標分類、語音識別等應用場景。