ICLR2025-MMFNET:用于多變量時間序列預測的多尺度頻率掩碼神經網絡
title:MMFNET: MULTI-SCALE FREQUENCY MASKING NEURAL NETWORK FOR MULTIVARIATE TIME SERIES FORECASTING
paper:https://arxiv.org/pdf/2410.02070
code:暫未公開
highlights:MMFNet 是一種新穎的模型,旨在通過多尺度頻率掩碼分解方法來增強長期多變量時間序列預測。該模型通過將時間序列轉換為不同尺度的頻率段,并使用可學習的掩碼自適應地過濾掉不相關的成分,從而捕捉細粒度、中間和粗粒度的時間模式。
-
MMFNet采用多尺度頻域分解方法,以捕捉頻域中的動態變化。
-
MMFNet利用可學習的頻率掩碼,根據時間序列片段的頻譜特性,自適應地過濾掉無關的頻率成分。
背景
雖然單尺度頻域分解提供了頻域中時間序列數據的全局視角,但它缺乏在序列中定位特定頻率分量的能力。此外,這種方法假設頻率分量在整個序列中保持不變,因此無法解釋在實際時間序列中經常觀察到的非平穩行為。此外,FITS 采用的低通濾波器可能會無意中消除準確預測所需的關鍵短期波動。低通濾波器的固定截止頻率可能不是各種時間序列數據集的普遍最佳頻率,這進一步限制了其適應性。
方法
在本文中,我們提出了 MMFNet,這是一種旨在通過多尺度掩蔽頻率分解方法增強 LTSF 的新模型。MMFNet 通過在多個尺度上分割時間序列,在頻域中捕獲精細、中等和粗顆粒模式。在每個尺度上,MMFNet 都采用可學習掩碼,根據路段的頻譜特性自適應地過濾掉不相關的頻率分量。MMFNet 提供了兩個關鍵優勢:
(i) 多尺度頻率分解使 MMFNet 能夠有效地捕獲數據的短期波動和更廣泛的趨勢;
(ii) 可學習的頻率掩碼自適應地過濾不相關的頻率分量,使模型能夠專注于信息量最大的信號。
這些功能使 MMFNet 非常適合在復雜的時間序列中捕獲短期和長期依賴關系,將其定位為各種 LTSF 任務的有效解決方案。
作者首先定義了什么是長時序列預測和單尺度頻率變換(SFT):
-
長時序列預測就是使用一段已知的歷史序列預測未來相當長度時間的值:
![image]()
-
而SFT 是指將時域數據在單個全局尺度上轉換為頻域而不對時間序列進行分割的過程。這種變換通常使用快速傅里葉變換 (FFT) 等方法執行,該方法可以有效地計算離散傅里葉變換 (DFT)。SFT 將整個信號分解為正弦分量,從而能夠分析其頻率成分。每個頻率分量可以表示為:
![image]()
盡管 SFT 能夠捕獲廣泛的時間模式,例如通過低通濾波捕獲長期趨勢或通過高通濾波捕獲短期波動,但其全局應用會統一處理整個信號。這種統一的處理可能會導致在不同尺度上發生的重要局部時間變化和非平穩行為的丟失。
基于此,作者定義了多尺度頻率變換:

相比但尺度頻率變換,MMFT 將信號劃分為多個尺度,每個尺度都經過頻率分解。在每個尺度上,都會應用可學習的頻率掩碼,以保留信息量最大的頻率分量,同時選擇性地丟棄噪聲。這種多尺度方法使模型能夠適應非平穩信號,捕獲跨越不同時間范圍的復雜依賴關系。通過利用多個尺度的頻率分解并應用自適應掩碼,MMFT 通過關注數據中的短期波動和長期趨勢來提高長期預測的準確性。這種方法提高了模型的靈活性和穩健性,特別適用于非平穩和多變量時間。

MMFNet 通過結合所提出的 MMFT 方法來捕獲不同尺度上復雜的頻率特征,從而增強時間序列預測。MMFNet 的整體架構如圖包括三個關鍵組件:多尺度頻率分解、掩蔽頻率插值和頻譜反轉。
多尺度 Frequency Decomposition
-
Fragmentation:
將時間序列數據分解為不同長度的段,以捕獲多個比例的特征:將歸一化后的輸入序列 X 分為三組片段:精細片段、中尺度片段和粗尺度片段。
精細分段 (Xf ine) 由較短的分段組成,這些分段捕獲時間序列的詳細高頻分量,從而能夠檢測在較長分段中可能遺漏的復雜模式和異常。
中級段 (Xintermediate) 長度適中,旨在捕捉中級形態和趨勢,在精細段和粗段之間取得平衡。
粗略尺度區段 (Xcoarse) 由較長的區段組成,這些區段捕獲數據中更廣泛的低頻趨勢和總體模式。
這種多尺度碎片化使模型能夠有效地捕獲和利用不同時間尺度的模式。 -
分解
將多尺度時域段轉換為相應的頻率分量,以捕獲各種時間尺度上的頻率模式。對于每個分段,應用 DCT 來提取頻域表示。
![image]()
這種轉換使 MMFNet 能夠在頻域中捕獲和分析多個時間尺度的模式,從而增強其識別和解釋時間序列數據中復雜模式的能力。
Masked Frequency Interpolation
掩碼頻率插值利用可學習的掩碼在頻域中自適應地過濾不同尺度的頻率分量,然后通過線性層神經網絡進行重建。這種方法使模型能夠學習和應用針對不同數據集量身定制的特定于比例的篩選策略。
-
掩碼
區別于傳統方法使用預定義截止頻率的固定低通濾波器來過濾頻率分量。因為這些方法假設某些頻率在整個時間序列中普遍重要或不相關,這一假設可能不適用于頻率分量相關性隨時間變化的非平穩數據。且這種過度過濾的方式會導致關鍵細節丟失,從而導致過度簡化的表示和模型在預測和信號分析等任務中的性能下降。為了避免以上問題,MMFNet 采用自適應屏蔽技術來捕獲頻域中的動態行為。給定頻率段 XDCT ,將生成一個可學習掩碼來自適應地過濾頻率分量。掩碼通過根據不同頻率分量與任務的相關性來減弱或強調它們,從而調整它們的重要性。此過濾過程通過元素乘法應用,表示為:
![image]()
這種自適應機制提高了模型捕獲有意義模式的能力,同時最大限度地減少了不相關或噪聲信息的影響。 -
插值
掩蔽的頻段 Xmask DCT 通過線性層轉換為預測的頻域段 Xpred DCT。此線性轉換將篩選后的頻率分量映射到與模型的預測目標一致的目標頻率表示。具體來說,將完全連接(密集)層應用于掩蔽頻率分量,此作可以表示為:
![image]()
這種轉換進一步細化了頻域信息,產生了 Xpred DCT ,這對于重建準確的時域預測至關重要。通過利用細化的頻率信息并減少不相關頻率分量的影響。
頻譜反轉Spectral Inversion
使用 iDCT 將插值的頻率分量轉換回時域,與之前的 DCT 過程相反。iDCT 單獨應用于預測的頻域段 X f ine pred DCT 、 Xintermediate pred DCT 和 Xcoarse pred DCT 。區段的 iDCT 由以下公式給出:

這個方程通過對每個頻率分量的貢獻求和來重建時域信號(Davis & Marsaglia, 1984)。
一旦對每個標度分別執行 iDCT,就會將得到的時域信號組合在一起。此積分步驟通過組合精細、中間和粗調的輸出來合并多尺度頻率信息。最終重建的信號保留了原始輸入的關鍵特性,同時結合了通過掩蔽頻率濾波實現的增強插值。
實驗

結論
MMFNet 通過采用 MMFT 方法顯著推進了長期多變量預測。通過對基準數據集的全面評估,我們證明 MMFNet 在預測準確性方面始終優于最先進的模型,凸顯了它在捕獲復雜數據模式方面的穩健性。通過將多尺度分解與可學習的掩碼濾波器有效地集成在一起,MMFNet 可以捕獲復雜的時間細節,同時自適應地減輕噪聲,使其成為適用于各種 LTSF 任務的多功能且可靠的解決方案。





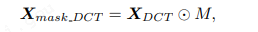


 浙公網安備 33010602011771號
浙公網安備 33010602011771號