大學物理期末急救指北

大學物理急救指北

更好的觀感？來我的網站趴！

剛體

平動和轉動的迅速溝通

	質點	剛體
運動方程	$F=ma$	$M=J\alpha$
動量/角動量	$p=mv$	$L=J\omega=mvr$
動量/角動量定理	$\int F\mathrm dt=\Delta p$	$\int M\mathrm dt=\Delta L$
動能	$E_k=\frac 12 mv^2$	$E_k=\frac 12 J\omega^2$
力/力矩做功	$W=\int F\mathrm dx$	$W=\int M\mathrm d\theta$

轉動慣量

\[\begin{gather} J=\sum m_ir_i^2=\int r^2\mathrm dm \end{gather} \]

質量分布離軸越遠，轉動慣量越大。空心物體比實心物體轉動慣量大。

常見物體的轉動慣量

形狀	轉動慣量
圓環(huán)、空心圓柱	$MR^2$
圓盤、實心圓柱	$\frac12 MR^2$
細桿（繞中點）	$\frac 1{12} ML^2$
細桿（繞端點）	$\frac 13 ML^2$

平行軸定理

剛體對于任意軸的轉動慣量=對于質心的轉動慣量+質量乘以兩個軸距離的平方

\[\begin{gather} J=J_c+md^2 \end{gather} \]

也就是換軸需要借助質心來換。

轉動定律

角加速度 $a$ 正比于合外力矩 $M=Fd$ ，反比于轉動慣量 $J=mL^2$。

\[\begin{align} M&=Fd\\ M&=Ja \end{align} \]

剛體的角動量守恒

角動量

\[\begin{gather} L=J\omega \end{gather} \]

角動量定理

外力矩對時間的積累等于角動量的變化

\[\begin{gather} \int_{t_1}^{t_2} M_外\mathrm dt=J\omega_2-J\omega_1 \end{gather} \]

角動量守恒定律

若外力矩為零，則角動量 $L=J\omega$ 不變。

若剛體繞著光滑軸旋轉，無其他外力，則角動量守恒。

例：人質量m在半徑R的水平平臺邊緣，平臺可繞其中心的豎直光滑固定軸旋轉，轉動慣量為J。平臺和人靜止。突然人以相對地面為v的速率在邊緣逆時針轉動行走，求此視平臺對于地面旋轉角速度

角動量守恒，且為零。

\[\begin{gather} 0=J\cdot w+m\cdot vR\\ \therefore \omega=-\frac{mvR}{J} \end{gather} \]

解釋：角速度大小為 $\frac{mvR}{J}$，方向與人行走方向相反。

剛體的動能

\[\begin{gather} E_k=\frac12 J\omega^2 \end{gather} \]

靜電場

電荷

電荷激發(fā)電場

\[Q=ne\quad e\approx1.602\times10^{-19}\rm C \]

孤立系統(tǒng)種總電荷量不變（正負電荷代數(shù)和不變）

庫倫定律

\[\begin{gather} \vec{F_{21}}=\frac{1}{4\pi \varepsilon_0}\frac{q_1q_2}{r^2}\vec{r_{21}} \end{gather} \]

通常會令 $k=\frac{1}{4\pi \varepsilon_0}$ 以簡寫，但是 $\pi \varepsilon_0$? 出現(xiàn)頻率挺高的。

$\varepsilon_0$ 是真空中的電介質常數(shù)，也稱為真空電容率，其值約為 $8.85 \times 10^{-12}$ 法拉/米（F/m）。

多個點電荷則矢量疊加，帶電導體則積分。

\[\begin{gather} \vec{E}=\frac{\vec{F}}{q_0} \end{gather} \]

場強：大小為單位電荷在該點受力的大小，方向為正電荷在該點受力方向。

點電荷的電場

\[\begin{gather} \vec{E}=\frac{\vec F}{q_0}=\frac{1}{4\pi \varepsilon_0}\frac{q}{r^2}\vec {r^0} \end{gather} \]

連續(xù)分布的帶電體

\[\begin{gather} \mathrm d\vec E=\frac{1}{4\pi \varepsilon_0}\frac{\mathrm dq}{r^2}\vec{r^0}\\ \vec E=\int\frac{\mathrm dq}{4\pi \varepsilon_0r^2}\vec{r^0}\\ \end{gather} \]

其中

\[\mathrm dq= \begin{cases} \lambda \mathrm dl&(體分布)&\lambda:線密度\\ \sigma \mathrm dS&(體分布)&\sigma:面密度\\ \rho \mathrm dV&(體分布)&\rho:體密度 \end{cases} \]

例：長為L的均勻帶電直桿，電荷線密度為$\lambda$，求其在空間一點P產生的電場強度，P到桿的垂直距離為a

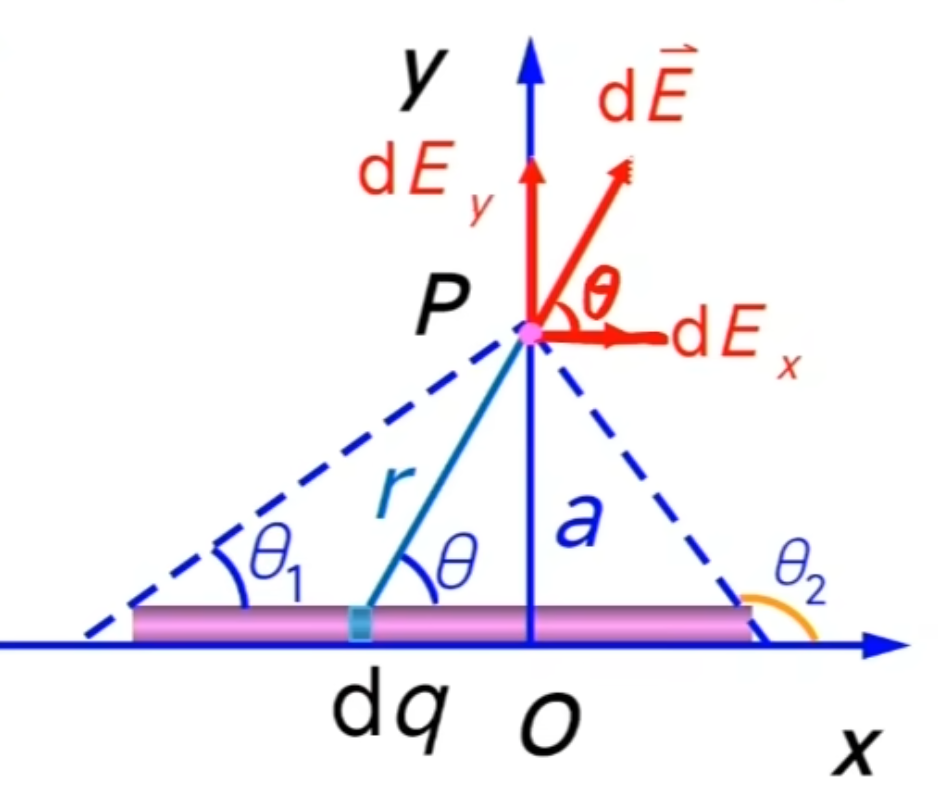$$ \begin{gather} \mathrm dq=\lambda \mathrm dx\\ \mathrm dE=\frac{1}{4\pi \varepsilon_0}\frac{\lambda\mathrm dx}{r^2}\\ \mathrm dE_x=\mathrm dE\cos\theta\\ \mathrm dE_y=\mathrm dE\sin\theta\\ x=a\tan(\theta-\frac{\pi}{2})=-a\cot\theta\\ \mathrm dx=a\csc^2\theta \mathrm d\theta\\ \nonumber\\ E_x=\int \mathrm dE_X=\int_{\theta_1}^{\theta_2}\frac{\lambda}{4\pi \varepsilon_0a}\cos\theta\mathrm d\theta\\ =\frac{\lambda}{4\pi\varepsilon_0a}(\sin\theta_2-\sin\theta_1)\\ \nonumber\\ E_y=\frac{\lambda}{4\pi\varepsilon_0a}(\cos\theta_2-\cos\theta_1) \end{gather} $$ *考試一般不考這種復雜的、位置不確定的。*

帶電桿的較遠處的場強

桿可以看成點電荷，$\theta_1=\theta_2$，所以有

\[\begin{gather} E_x=0,E_y=\frac{\lambda L}{4\pi \varepsilon_0a^2}=\frac{1}{4\pi \varepsilon_0}\frac{\lambda L}{a^2} \end{gather} \]

無限長直導線場強

$\theta_1=0,\theta_2=180^\circ$

\[\begin{gather} E_x=0,E_y=\frac{\lambda}{2\pi \varepsilon_0a} \end{gather} \]

例：半徑為R的均勻帶電圓環(huán)，帶電量q。求圓環(huán)周先上任意一點P的電場強度

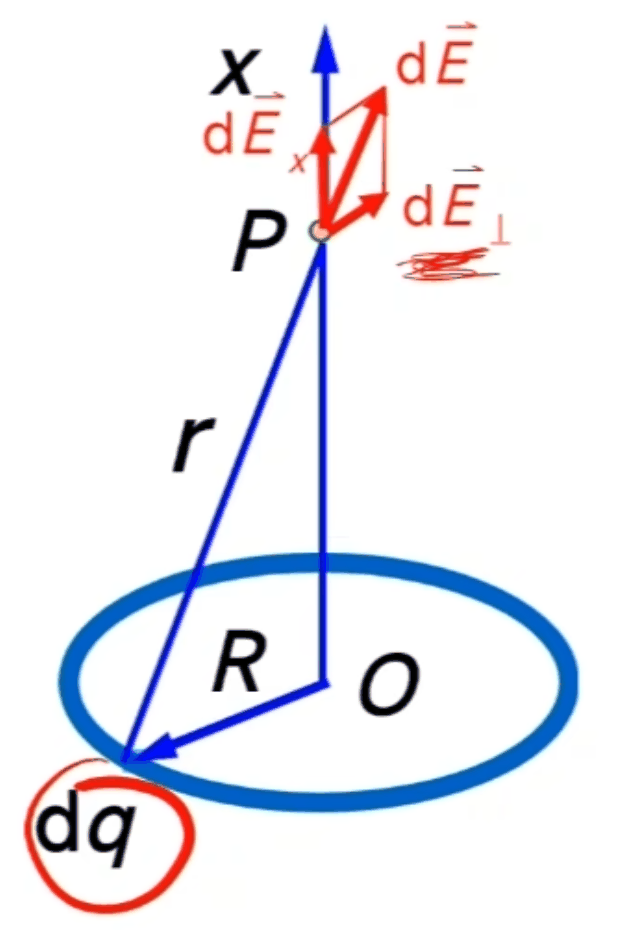$$ \begin{gather} \mathrm dq=\lambda \mathrm dl\\ \mathrm dE=\frac{1}{4\pi \varepsilon_0}\frac{\mathrm dq}{r^2}\\ \mathrm dE_\perp=0(對稱性)\\ \mathrm dE_x=\mathrm dE\cos \theta \end{gather} $$

\[\begin{align} E_x&=\frac{1}{4\pi\varepsilon_0}\int\frac{\mathrm dq}{r^2}\cos\theta\\ &=\frac{1}{4\pi \varepsilon_0}\frac{\cos\theta}{r^2}\int\mathrm dq\\ &=\frac{1}{4\pi \varepsilon_0}\frac{\cos\theta}{r^2}q\\ &=\frac{1}{4\pi \varepsilon_0}\frac{qx}{(R^2+x^2)^{\frac32}} \end{align} \]

帶電圓環(huán)在圓心處場強

$E=0$

帶電圓環(huán)在無窮遠處場強

$x\gg R$，可以將圓環(huán)視作點電荷，$E=\frac1{4\pi\varepsilon_0}\frac{q}{x^2}$?

例：面密度為$\sigma$的圓板在軸線上任一點的電場強度

之前是$\mathrm dq$在$L$上積分，所以$\mathrm dq=\lambda \mathrm dl$

在板子上，是以一個環(huán)作為一個小量進行積分。

每個小環(huán)=環(huán)的周長乘以環(huán)的寬度$\mathrm dr$

\[\begin{gather} \mathrm dq=2\pi r\mathrm dr \end{gather} \]

或者，$\mathrm dq=\sigma\mathrm dS=\sigma\mathrm d(\pi r^2)$，本質上是一樣的。

\[\begin{gather} \mathrm dE=\frac1{4\pi \varepsilon_0}\frac{x\mathrm dq}{(r^2+x^2)^\frac32}\\ E=\int \mathrm dE= \frac{x\sigma}{2\varepsilon_0}\int_0^R\frac{r\mathrm dr}{(r^2+x^2)^\frac32}\\ =\frac \sigma {2\varepsilon_0}[1-\frac{x}{(R^2+x^2)^\frac12}] \end{gather} \]

電場線與電通量

由正電荷指向負電荷或無窮遠處
切線反映方向，疏密反映場強大小
非閉合曲線
不相交

電通量：穿過曲面S的電場線條數(shù)

\[\begin{gather} \mathrm d\phi_e=E_n\mathrm dS=E\cos\theta\mathrm dS=E\mathrm dS_\perp \end{gather} \]

非均勻場：對S積分

\[\begin{gather} \phi_e=\int \mathrm d\phi_e=\int_S\vec E\cdot \mathrm d\vec S \end{gather} \]

高斯定理

\[\begin{gather} \phi_e=\oint_S\vec E\cdot \mathrm d\vec S=\frac 1 {\varepsilon_0}\sum_i q_i=\frac1{\varepsilon_0}\int_V \rho\mathrm dV \end{gather} \]

穿過閉合曲面的電通量在數(shù)值上等于曲面內包圍的電量的代數(shù)和乘以$\frac1{\varepsilon_0}$

例：均勻帶電球面，總電量Q，半徑R。求某點處E

對于球面外一點P：

取過P的同心求面為高斯面，表面積$4\pi r^2$。對于高斯面上每一個dS，都會有大小為E的場強穿過。

\[\begin{gather} \phi_e=\oint_S \vec E\cdot \mathrm d\vec S=\oint_S E\mathrm dS=E\oint_S\mathrm dS=E\cdot 4\pi r^2\\ \phi_e=\frac1{\varepsilon_0}\sum_i q_i=\frac1{\varepsilon_0}Q\\ \therefore E=\frac{Q}{4\pi\varepsilon_0 r^2} \end{gather} \]

由于電荷在球面上分布，內部無電荷，所以 $r<R$ 時 $E=0$。

帶電量為q的球體半徑為R，電荷體密度為$\rho$。求某點處E

$r>R$ 時，同上；

$r<R$ 時，$E\not=0$。只有$\le r$部分的電荷有作用：

\[\begin{gather} E\cdot 4\pi r^2=\frac1 {\varepsilon_0}\int_0^r\rho\mathrm dV=\frac1{\varepsilon_0}\rho\frac43\pi r^3\\ \therefore E=\frac{\rho}{3\varepsilon_0}r \end{gather} \]

無限大均勻帶電板上電荷面密度為$\rho$，求E分布

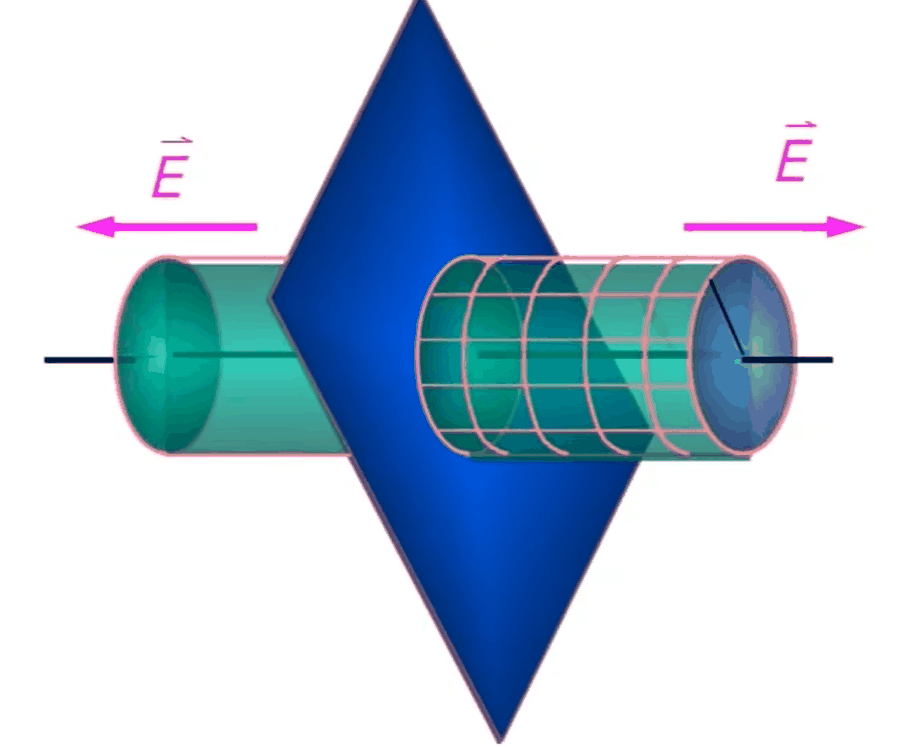
如上圖選取高斯面

\[\begin{gather} \phi_e=\int_{側面}\vec E\cdot \mathrm d\vec S+\int_{左底}\vec E\cdot \mathrm d\vec S+\int_{右底}\vec E\cdot \mathrm d\vec S\\ =0+ES+ES=2ES\\ 2ES=\frac1{\varepsilon_0}\sigma S\\ E=\frac{\sigma}{2\varepsilon_0} \end{gather} \]

電勢

單位正電荷從該點移動到勢能零點過程中，電場力做的功。

\[u_a=u_{a0}=\int_a^{0}\vec E\cdot \mathrm d\vec l \]

點電荷的電勢

\[\begin{gather} u_a=\int_a^\infty \vec E\cdot \mathrm d\vec l=\frac{q}{4\pi \varepsilon_0}\int_r^\infty\frac{\mathrm dr}{r^2}=\frac{q}{4\pi \varepsilon_0 r} \end{gather} \]

電容

\[\begin{gather} E=\frac Ud\\ C=\frac QU=\frac{\varepsilon_0\varepsilon_rS}w0obha2h00\\ W=\frac12CU^2\\ \end{gather} \]

例：將平行電容板充電后與電源斷開，將其$d$拉大，問電勢差$U_{12}$、電場強度$E$、電場能量$W$的變化

電源斷開，所以$Q$不變

\[\begin{gather} C\downarrow\propto\frac{S}{d\uparrow}\\ U\uparrow=\frac{Q}{C\downarrow}\\ E=\frac{U\uparrow}{d\uparrow}=\frac{Q}{C\downarrow d\uparrow}\propto \frac{Q}{S}\\ W\uparrow=\frac12 C\downarrow U^2\uparrow\propto U\uparrow \end{gather} \]

恒定磁場

電流強度

\[\begin{gather} I=\frac{\mathrm dq}{\mathrm dt}=\frac Qt \end{gather} \]

是一個標量，但是為了電路處理方便，規(guī)定正電荷移動方向是電流方向。

磁感應強度

小磁針在磁場中，北極N的指向為 $\vec B$ 的方向。

畢薩定律

大小

\[\begin{gather} \mathrm d\vec B=\frac{\mu_0}{4\pi}\frac{I\mathrm d\vec l\times \vec r_0}{r^2} \end{gather} \]

方向：右手螺旋定則，從 $I\mathrm d\vec l$ 握到 $\vec r_0$，也可以大拇指順電流手握導線。

載流直導線的磁場

求距離載流直導線為a處的一點P的磁感應強度$\vec B$

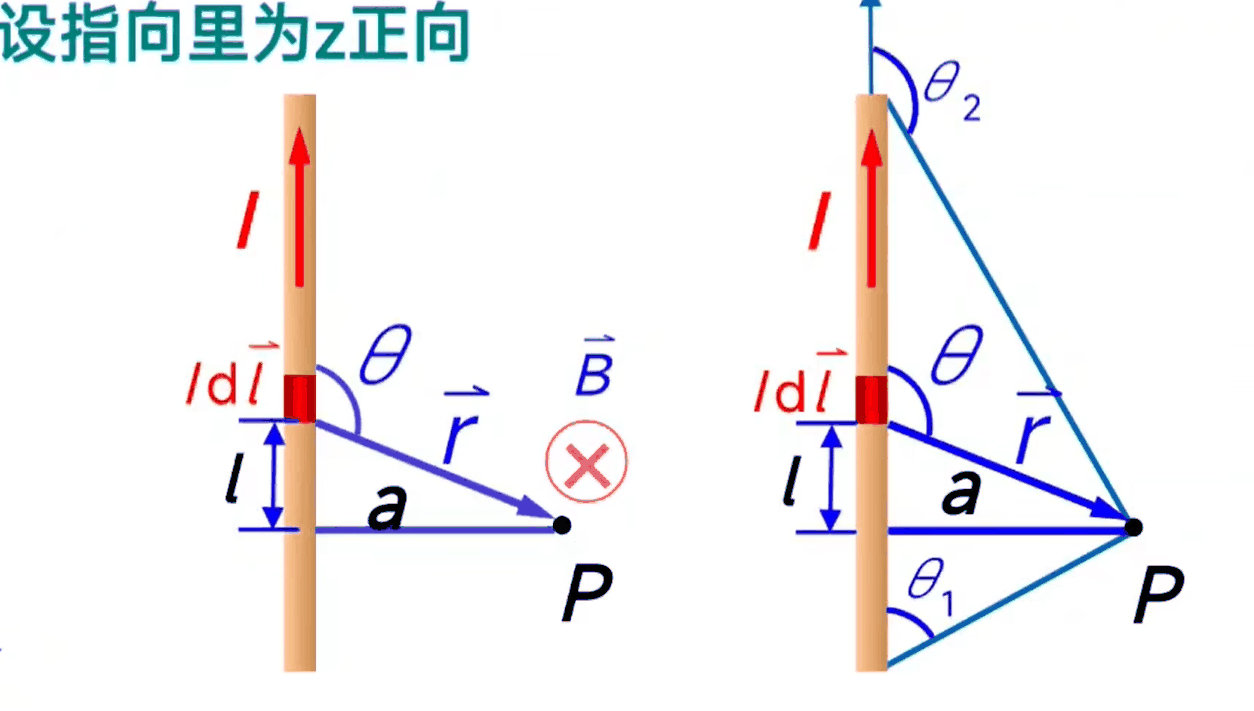$$ \begin{gather} \mathrm dB=\frac{\mu_0}{4\pi} \frac{I\mathrm dl\sin\theta}{r^2}\\ r=a\csc\theta\\ l=a\cot(\pi-\theta)=-a\cot\theta\\ \mathrm dl=a\csc^2\theta\mathrm d\theta\\ B_z=B=\int\frac{\mu_0}{4\pi} \frac{I\mathrm dl\sin\theta}{r^2}=\frac{\mu_0I}{4\pi a}(\cos\theta_1-\cos\theta_2)

\end{gather}

\[*如果把 $\theta_2$ 換成三角形的內角更好記一點，就是 $\frac{\mu_0I}{4\pi a}(\cos\theta_1+\cos\theta_2)$ 了* **無限長直導線的磁場** $\theta_1\to 0,\theta_2\to \pi$ \]

\begin{gather}
B=\frac{\mu_0I}{2\pi a}
\end{gather}

\[**任意形狀直導線** 分成多段直導線，矢量疊加 --- **載流圓線圈的磁場** > 半徑 $R$ 的載流 $I$ 圓線圈上一點 $P$ 的磁感應強度 <img src="https://vanilla-picture-with-picgo.oss-cn-shenzhen.aliyuncs.com/img-from-OSS-uploader/20240622-140935-80854.png" alt="alt" max-width="240" height="180" border="10" /> \]

\begin{gather}
\mathrm dB=\frac{\mu_0I\mathrm dl}{4\pi r^2}=\frac{\mu_0I\mathrm dl}{4\pi(R^2+x2)}\
B_\perp=0\
B=\int\mathrm dB\cos\theta=\int\frac{\mu_0}{4\pi}\frac{I\mathrm dl}{r^2}\cos\theta\
=\int\frac{\mu_0}{4\pi}\frac{I\mathrm dl}{r^2}\frac Rr=\frac{\mu_0IR}{4\pi(R^2+x2)^\frac 32}2\pi R\
=\frac{\mu_0IR^2}{2(R2+x²⁾\frac32}
\end{gather}

\[**載流圓線圈圓心處** $x=0$ \]

\begin{gather}
B=\frac{\mu_0I}{2R}
\end{gather}

\[**一段載流圓弧圓心處** 圓弧所對的圓心角為$\phi$ \]

\begin{gather}
B=\frac{\mu_0I}{2R}\cdot\frac{\phi}{2\pi}
\end{gather}

\[ --- **繞軸旋轉的帶電圓盤軸線上的磁場** > 帶電 $q$ 的圓盤以角速度 $\omega$ 旋轉，求軸線上 $x$ 處磁場 \]

\begin{gather}
\sigma=\frac{q}{\pi R^2}\
\mathrm dq=\sigma\cdot2\pi r\mathrm dr\
\mathrm dI=\frac{\mathrm dq}{\mathrm dt}=\frac{\sigma\cdot2\pi r\mathrm dr}{2\pi\omega}=\omega \sigma r\mathrm dr\
\mathrm dB=\frac{\mu_0r^2\mathrm dI}{2(r^2+x2)^\frac32}\
=\frac{\mu_0\sigma\omega r^3\mathrm dr}{2(r^2+x2)^\frac32}\
B=\frac{\mu_0\sigma\omega}2[\frac{R^2+2x2}{\sqrt{x^2+R2}}-2x]

\end{gather}

\[ ## 磁感線 1. 無頭無尾閉合曲線 2. 與電流套連，服從右手螺旋 3. 不相交磁通量：通過某個面元的磁感線條數(shù) 規(guī)定磁感線穿入$\phi_m<0$，穿出$\phi_m>0$ **磁感線的高斯定理** 由于磁感線閉合，所以 \]

\begin{gather}
\phi_m=\oint_S\vec B\cdot\mathrm d\vec S=0
\end{gather}

\[**磁場的安培環(huán)路定理** 電場中，繞一圈回來，電場力不做功；磁場中則與環(huán)路包圍著的電流有關： \]

\begin{gather}
\oint_L\vec B\cdot \mathrm d\vec l=\mu_0I
\end{gather}

\[要求： 1. 環(huán)路 $L$ 與 $B$ 同向。如果 $L$ 反向，則為$-\mu_0I$。 2. 對于一段導線不成立。只適用于閉合導線 ## 安培定理 \]

\begin{gather}
\mathrm dF=I\mathrm d\vec l\times \vec B
\end{gather}

\[ 注意方向，$\vec l\times \vec B$ **均勻磁場中形狀任意的導線受力** 電流強度為 $I$ 等價于起點與終點連線的導線的受力 $F=BIL'$ **平行無限長直導線之間的相互作用力** \]

\begin{gather}
B_1=\frac{\mu_0I_1}{2\pi a}\
(單位長度受到的作用力)f_{12}=I_{2}B_1=\frac{\mu_0I_1I_2}{2\pi a}
\end{gather}

\[電流同向相吸，異向排斥。 ## 洛倫茲力安培力是大量粒子洛倫茲力的疊加對一個電荷研究 \]

\begin{gather}
\vec f_m=q\vec v\times \vec B
\end{gather}

\[代入$I=envS\Rightarrow v=\frac{I}{enS}$ \]

\begin{gather}
f_m=qvB=\frac{BI}{nS}
\end{gather}

\[做圓周運動 \]

\begin{gather}
qvB\sin\frac\pi2=m\frac{v^2}{R}\
R=\frac{mv}{qB}\
T=\frac{2\pi R}{v}=\frac{2\pi m}{qB}\
f=\frac{qB}{2\pi m}
\end{gather}

\[ # 電磁感應 ## 電磁感應定律 \]

\begin{gather}
\phi=\int\vec B\cdot\mathrm d\vec S\
\varepsilon=-\frac{\mathrm d\phi}{\mathrm dt}
\end{gather}

\[ 負號表示方向，阻礙磁通量的變化（楞次定律）若回路中有電阻 $R$ \]

\begin{gather}
I_i=\frac \varepsilon R=-\frac{\mathrm d\phi}{R\mathrm dt}=\frac{\mathrm dq_i}{\mathrm dt}\
感應電荷q_i=\int_{t_1}^{t_2}-\frac1R\mathrm d\phi=\frac{\phi_1-\phi_2}R
\end{gather}

\[ > 例：大小同心圓環(huán)，$r_1\ll r_2$，大線圈有電流$I$，當小線圈環(huán)繞其直徑以 $\omega$ 轉動時，求小圓環(huán)中的感應電動勢大圓環(huán)在圓心處的磁場 \]

\begin{gather}
B=\frac{\mu_0I}{2r_2}
\end{gather}

\[通過小線圈的磁通量 \]

\begin{gather}
\phi=\vec B\cdot \vec S=\frac{\mu_0I}{2r_2}\pi r_1^2cos\omega t
\end{gather}

\[所以感應電動勢 \]

\begin{gather}
\varepsilon=-\frac{\mathrm d\phi}{\mathrm dt}=\frac{\mu_0I\pi r_1^2\omega}{2r_2}\sin\omega t
\end{gather}

\[ --- > 例：無限載流長直導線的磁場中，一運動導體線框以速度 $v$ 作遠離導線運動，且始終與長直導線共面。求線框的感應電動勢 <img src="https://vanilla-picture-with-picgo.oss-cn-shenzhen.aliyuncs.com/img-from-OSS-uploader/20240622-202023-12317.png" alt="alt" max-width="240" height="180" border="10" /> \]

\begin{gather}
\mathrm d\phi=B\mathrm dS=\frac{\mu_0I}{2\pi x}b\mathrm dx\
\phi=\int_L^{L+a}\mathrm d\phi\
=\frac{\mu_0Ib}{2\pi}\int_L^{L+a}\frac{\mathrm dx}x\
=\frac{\mu_0Ib}{2\pi}\ln\frac{L+a}{L}\
L=vt,\mathrm dL=v\mathrm dt\
\varepsilon=-\frac{\mathrm d\phi}{\mathrm dt}=-\frac{\mu_0Ib}{2\pi}[\frac{\frac{\mathrm dL}{\mathrm dt}}{L+a}-\frac
{\frac{\mathrm dL}{\mathrm dt}}{l}]\
=\frac{\mu_0Iabv}{2\pi L(L+a)}
\end{gather}

\[ ## 感應電動勢兩種感應機制 1. 動生電動勢：磁場不變，回路運動切割磁感線 2. 感生：回路靜止，磁場隨時間變化 ### 動生電動勢其原理是電子受洛倫茲力 \]

\begin{gather}
\vec f=-e(\vec v\times \vec B)
\end{gather}

\[即非靜電力$\vec F_k$ \]

\begin{gather}
\vec E_k=\frac{\vec F_k}{-e}=\vec v\times \vec B\
\varepsilon_i=\int_-^+\vec E_k\cdot \mathrm d\vec l=\int_-^+(\vec v\times \vec B)\cdot \mathrm d\vec l
\end{gather}

\[ > 例：勻強磁場 $B$ 中，長為 $R$ 的銅棒繞其一端 $O$ 以角速度 $\omega$ 在垂直于 $B$ 的平面內轉動，求棒上的電動勢方法一（動生電動勢） <img src="https://vanilla-picture-with-picgo.oss-cn-shenzhen.aliyuncs.com/img-from-OSS-uploader/20240622-212543-34750.png" alt="alt" max-width="240" height="180" border="10" /> \]

\begin{gather}
\varepsilon_i=\int_O^A(v\times B)\cdot \mathrm dl\
=\int_0^R l\omega B\mathrm dl\
=\frac{BR^2}{2}\omega
\end{gather}

\[用右手螺旋法則判斷方向為$A\to O$。方法二（法拉第電磁感應定律） <img src="http://vanilla-picture-with-picgo.oss-cn-shenzhen.aliyuncs.com/img-from-OSS-uploader/20240622-212922-53486.png" alt="alt" max-width="240" height="180" border="10" /> 在$\mathrm dt$的時間內導體切割磁感線，切割了一個扇形 \]

\begin{gather}
\mathrm d\phi=B\cdot\frac12 R^2\mathrm d\theta\
\varepsilon_i=\frac{\mathrm d\phi}{\mathrm dt}=\frac12 BR^2\frac{\mathrm d\theta}{\mathrm dt}=\frac12BR^2\omega
\end{gather}

\[由楞次定律，電流應當產生一個向外的點磁場來阻止其增大。為了在圖中扇形區(qū)域產生“點”場，電流$O\to A$ ### 感生電動勢 $\varepsilon_i=\int_a^b\vec E_v\cdot \mathrm d\vec l$，其中$\vec E_v$是感生電場感生電場與變化磁場之間的關系 \]

\begin{gather}
\oint_L\vec E_v\cdot \mathrm d\vec l=-\int_S\frac{\partial \vec B}{\partial t}\cdot \mathrm d\vec S
\end{gather}

\[即，感生電動勢=感生電場對于長度的積分=負的(磁場關于時間的變化量)對于平面的積分。 \]

posted @ 2025-04-25 15:05 Vanilla_chan 閱讀(143) 評論(0) 收藏舉報

刷新頁面返回頂部

	質點	剛體
運動方程	\(F=ma\)	\(M=J\alpha\)
動量/角動量	\(p=mv\)	\(L=J\omega=mvr\)
動量/角動量定理	\(\int F\mathrm dt=\Delta p\)	\(\int M\mathrm dt=\Delta L\)
動能	\(E_k=\frac 12 mv^2\)	\(E_k=\frac 12 J\omega^2\)
力/力矩做功	\(W=\int F\mathrm dx\)	\(W=\int M\mathrm d\theta\)

折柳