2.3 3D游戲所需要的數學知識

2.3.1 向量

向量的加減法遵循平行四邊形法則；

可以想象在Unity 中有兩個單位向量，分別位于X軸和Y軸上，二者的和、差：

Unity中物體的前后左右上下方向：

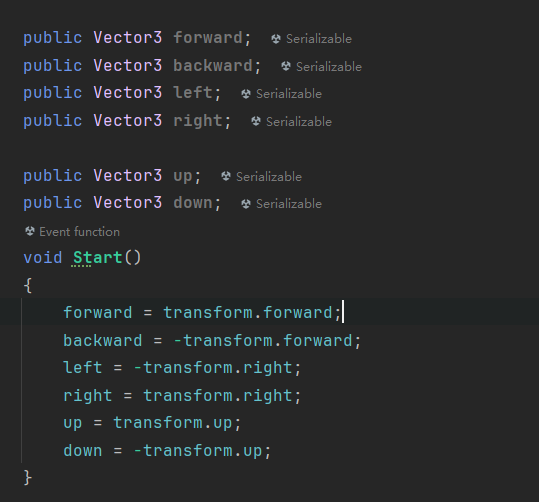
2.3.2 點乘

點乘是向量的數量積、也叫內積（外積是叉乘）。這里我們記住兩點就好，（死去的高中知識又來了）

點乘運算：

兩向量的點乘結果的正負表示兩向量的方向相近程度：（這里兩向量均為標量：長度為一的向量）

所以使用點乘可以判斷敵人在主角的左前方還是右前方。

例如在推箱子游戲中，判斷箱子在主角的方位：

 void PushBox(Transform playerTransform, Transform boxTransform)
 {
            const float ERROR = 0.5f;
            //箱子正面
            if (Vector3.Dot(playerTransform.forward, -boxTransform.forward) > ERROR)
            {
                //省略具體執行代碼
            }
            else if (Vector3.Dot(playerTransform.forward, boxTransform.forward) >
                     ERROR)                                                       //箱子背面
            {
                //省略具體執行代碼
            }
            else if (Vector3.Dot(playerTransform.forward, boxTransform.right) >
                     ERROR)                                                       //箱子左邊
            {
                //省略具體執行代碼
            }
            else if (Vector3.Dot(playerTransform.forward, -boxTransform.right) >
                     ERROR)                                                       //箱子右邊
            {
                //省略具體執行代碼
            }
  }

2.3.3 叉乘

叉乘，向量積、外積。兩向量的叉乘結果仍舊是向量。結果向量是垂直于兩乘數向量所在平面的。

（Unity中的世界坐標系是左手坐標系，所以圖示的叉乘結果方向是對應上的）

叉車在shader中有一個經典的運用：法向方向和切線方向的叉乘結果方向為副法線方向；

var bionormal = cross(normal,tangent)

同樣我們在Unity可以根據向量的叉乘來判斷敵人在主角的左邊還是右邊；

bool IsEnemyInRight(Transform playerTransform, Transform enemyTransform)
{
    //Unity中，向量的叉積結果的z軸的正負號可以判斷兩個向量的相對位置
    //如果叉積的z軸為正，說明敵人在玩家的右 方
    var cross = Vector3.Cross(playerTransform.forward, enemyTransform.position - playerTransform.position); 
    return Vector3.Dot(cross, playerTransform.up) > 0;
}

但需要注意，這個做法只存在于默認引力方向的情況下，對于存在改變引力的游戲，還需加入一些額外的邏輯處理。

其實這種方向判斷多用在2D游戲中，因為2D僅僅在XOY組成的平面上，可以直接通過簡單的叉乘或者點乘來判斷一個物體對于另一個物體的方位。在3D空間中的位置關系有多個維度，僅僅通過單一的判斷顯然不大可能。（左上前方、右下后方等等）

2.3.4 投影

投影跟向量的點乘有點關聯，即向量的點乘結果比上一個向量的模便得到另一個向量在本向量上的投影了。

應用：

在固定視角的第三人稱游戲中我們需要讓主角的移動方向和當前相機方向保持一致，而不是自身的正向方或者正右方。

也就是說視角看向哪里，但是只能在地面上行走（不考慮直升直降 Z軸空間上的移動），所以要把攝像機正前方、右方像投影在XOY平面上，得到真實的可以移動的方向。

 void UpdateMove(float speed)
        {
            var horizontal = Input.GetAxis("Horizontal");
            var vertical = Input.GetAxis("Vertical");

            var upAix = Physics.gravity.normalized;

            //攝像機正前方 在 與重力方向垂直的 XOY平面上的投影
            var forwardAxis = Vector3.ProjectOnPlane(Camera.main.transform.forward, upAix);
            //攝像機正右邊 在 與重力方向垂直的 XOY平面上的投影
            var rightAxis = Vector3.ProjectOnPlane(Camera.main.transform.right, upAix);
            
            //真正的前行方向
            var realMoveForwardAxis = (forwardAxis * vertical + rightAxis * horizontal).normalized;
            
            //再進行真實的移動
            transform.position += realMoveForwardAxis * speed * Time.deltaTime;
        }

2.3.5 四元數

歐拉角旋轉會造成萬向節死鎖問題，所以有關旋轉使用最多的是四元數。

通常我們用角-軸 去表示一個物體的旋轉。

//將物體繞著自身右軸旋轉-90度
transform.rotation = Quaternion.AngleAxis(-90,transform.right);

和歐拉角不同的是四元數可以不斷累乘，開發者可以把每一個旋轉步驟分開表示并在最終將它們相乘。四元數和矩陣相乘類似，但必須注意相乘的左右順序：

var rotationA = Quaternion.AngleAxis(35, Vector3.forward);
var rotationB = Quaternion.AngleAxis(45, Vector3.right);
transform.rotation = rotationA * rotationB;

 var rotationA = Quaternion.AngleAxis(35, Vector3.forward);
 var rotationB = Quaternion.AngleAxis(45, Vector3.right);
 transform.rotation = rotationB * rotationA;

上面兩幅圖展現出不同的先后旋轉順序對應兩種不同的旋轉結果；

利用累計乘積可以表示一個轉向效果：

  private void OnEnable()
  {
  	//旋轉開始方向 終止方向
  	mFromTo = Quaternion.FromToRotation(transform.forward, Vector3.forward);
  }

void Update()
{
	transform.rotation = Quaternion.Lerp(transform.rotation, mFromTo, 0.1f * Time.deltaTime);
}

FromTo表示對象是從當前Forward方向插值到世界Forward方向，我們將它放到Update里的每一幀去更新。

假如想要知道什么時候插值即將完成，則可以用四元數點乘去判斷，它和向量點乘類似，不一樣的是其結果會不斷接近-1, 1兩個零界點，這里用絕對值來進行判斷，代碼如下：