淺談二維凸包

二維凸包的定義

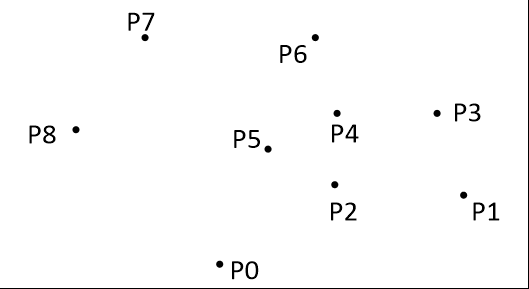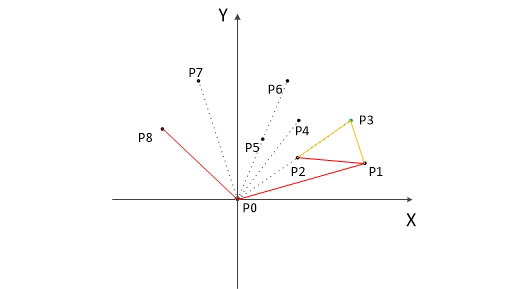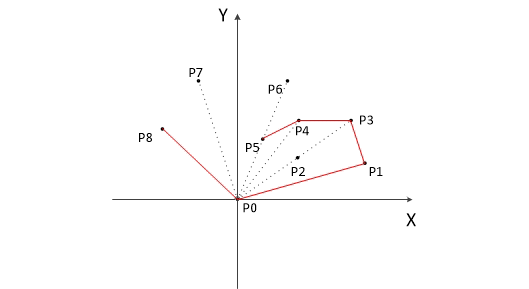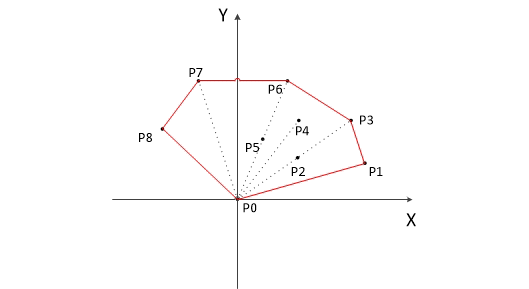
我們先看一張圖：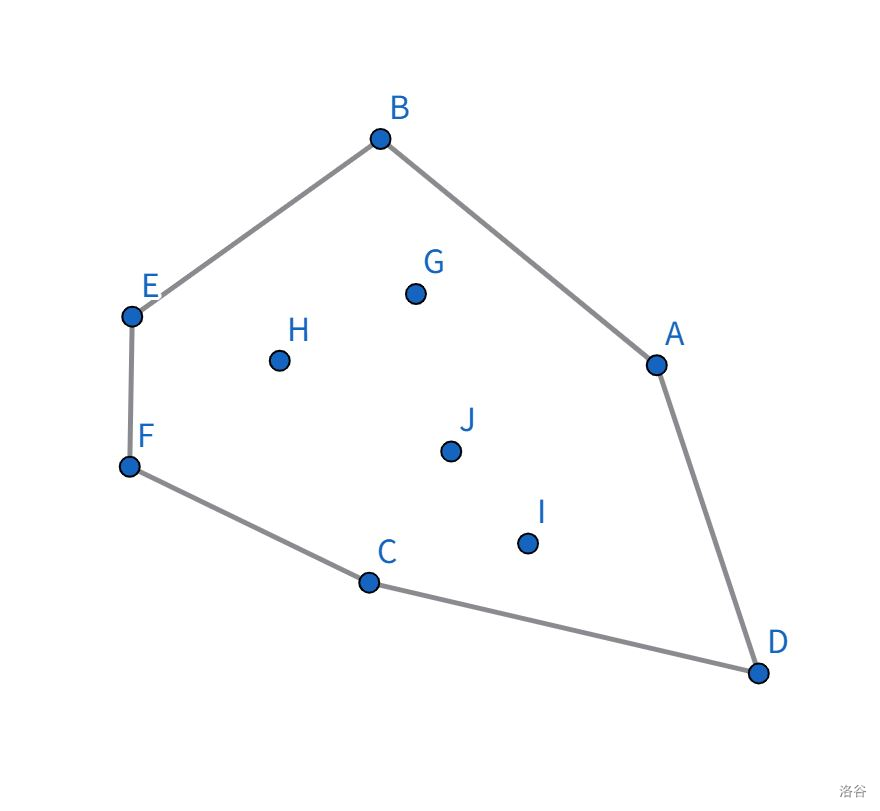

在這張圖片里，一個平面上有數個點，同時還有一個凸多邊形將這數個點完全覆蓋，那么使這個圖形面積最小的凸多邊形就稱為凸包。更具象化地講，就是用手撐開一個橡皮筋并用其把一堆釘子圍住，然后再松開手使橡皮筋收縮，那么最終橡皮筋形成的圖形便是這些釘子的凸包。

二維凸包的求法

本文章主要介紹使用 Graham 算法求解二維凸包。

Graham 算法

我們先介紹幾個前置知識；

• 極角
• 向量叉積

極角

極角指的是在極坐標中，平面上任意一點到極點的連線與極軸的夾角，如圖：

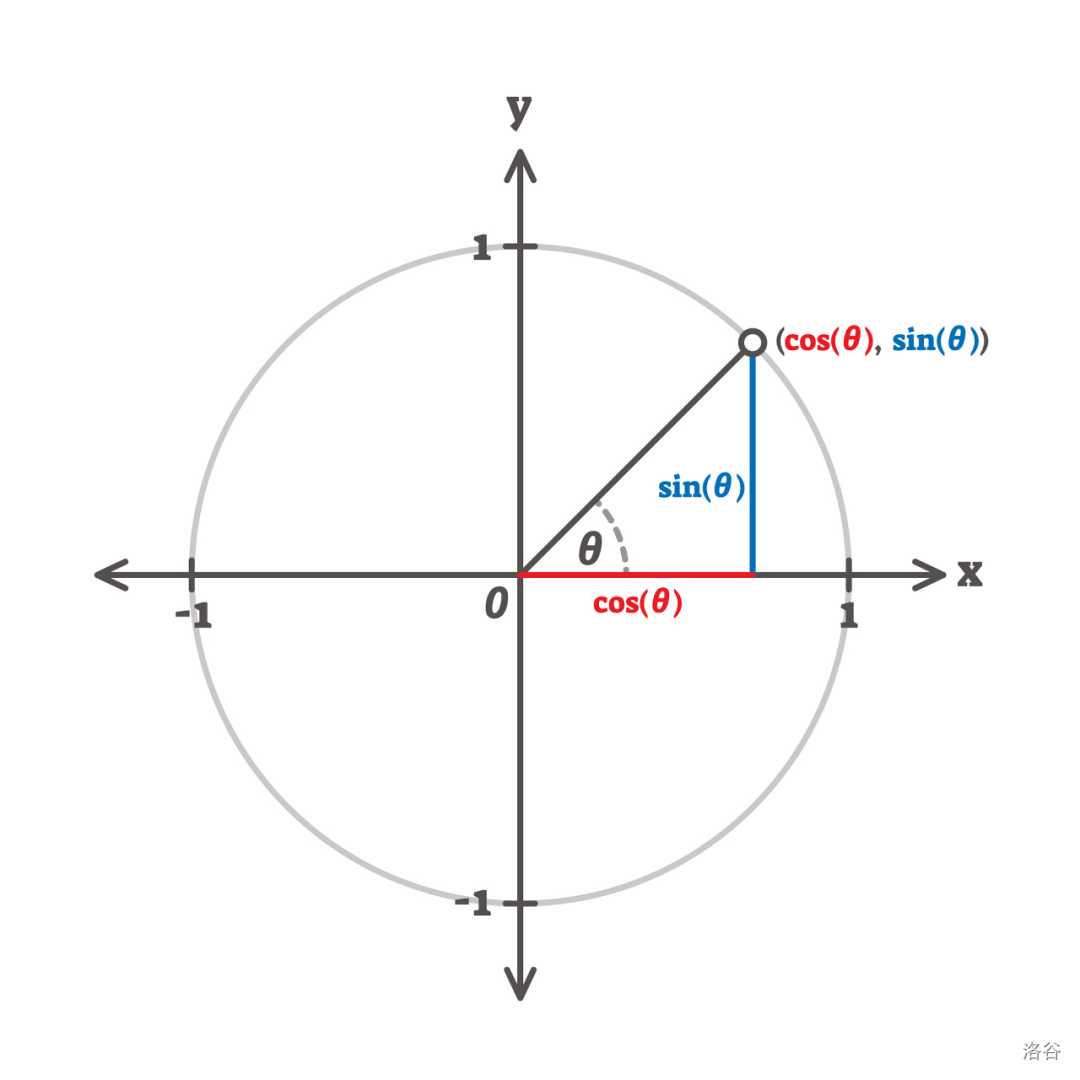
我們設 \(x\) 為 \(\cos(\theta)\)，\(y\) 為 \(\sin(\theta)\)。則：

這個公式在進行按極角大小排序時將會很有用。

向量叉積

向量叉乘是有大小有方向，并且不滿足交換律的運算。在求解凸包的過程中，我們并不關心向量的大小，而是關心后者，即其方向。由于向量的運算滿足右手法則，所以當兩向量的叉積為正時，后一個向量便在前者的左邊，在下文稱之為左拐；否則，若兩向量的叉積為負，那么后一個向量便在前者的右邊，在下文稱之為右拐。如下圖：

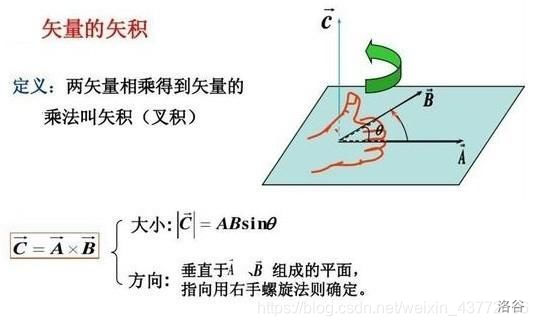
通過該運算，我們可以很清楚的判斷兩向量的位置關系，這在使用 Graham 算法求解凸包中發揮著很大的作用。

Graham 算法求解凸包

下面我將先介紹一下該算法求解凸包的流程：

1. 首先選取一個 \(y\) 坐標最小的點作為起始節點，如果有多個點的 \(y\) 坐標相同，那就選擇 \(x\) 坐標做小的點，此點必為凸包上的點。
2. 令起始節點為極坐標原點，按平面內其它點的極角從小到大進行排序，如果極角相同，按其到原點的距離從大到小排序。
3. 按排序后的順序將原點和第一個點加入到一個棧中。
4. 依次遍歷排序后的點，每遍歷到一個點時將棧頂的點和棧頂下面的點連線得到直線 \(l\)，然后判斷遍歷到的新點與棧頂元素所連成的直線與 \(l\) 為左拐、右拐或者處在同一直線上。如果是右拐或在同一直線上，則執行步驟五；否則執行步驟六。
5. 棧頂元素不在凸包上，出棧，執行步驟四。
6. 新點已處于凸包上，入棧。
7. 如果此時排序后的最后一個點已入棧，那么算法結束，否則執行步驟四。

最后，棧中的所有元素便是凸包上的點了。

模擬算法流程的動圖如下（在這幅圖中先選取的時橫坐標最小的點，但本質上都是一樣的）：

正確性證明

我們將通過兩個方面證明該算法正確性。

棧中所有點均為凸包頂點

• 原點為凸包頂點：因為原點 \(y\) 坐標以及 \(x\) 坐標均為最小的，所以它必然為凸包頂點。
• 棧中其它點均為凸包頂點：假設棧中有一點 \(p\) 不為凸包頂點，那么 \(p\) 必為凸包邊上或內部一點。但因為每次遇到在同一直線上或者在棧頂元素連線的右邊的點時都會彈出棧頂元素（即步驟四），這樣，便使得凸包內部和邊上的點均被彈出。所以凸包邊上和內部的點必然不會在算法結束后出現在棧內。

凸包頂點均在棧內

假設凸包頂點 \(q\) 不在棧內，那么 \(q\) 必然在算法進行時存在后繼點 \(q_1\) 使得 \(q\) 和 \(q_1\) 所連成的直線與 \(q\) 和原棧中的元素所連成的直線右拐。但因為在進行極角排序以后，凸包的頂點必然逆時針排列，即凸包的任意連續的三個頂點 \(p_{i-1}, p_i, p_{i+1}\) 均滿足左拐。所以在處理凸包頂點 \(q\) 與后繼節點 \(q_1\) 時必滿足左拐，所以 \(q\) 必然在棧內。

時間復雜度分析

在算法過程中極角排序的時間復雜度為 \(O(n\log n)\)，而每個點只會入棧和出棧一次，所以時間復雜度為 \(O(n)\)。總時間復雜度為 \(O(n\log n)\)，效率較高。

代碼實現（實現語言為 C++）

對于極角排序，我們可以使用內置的 atan2 函數，即計算 \(\arctan\) 值。而每次判斷棧頂元素是否需要出棧便相當于判斷此時棧頂的兩個點 \(A\)，\(B\) 和 新點 \(C\) 是否滿足 \(\overrightarrow{AB}\) 與 \(\overrightarrow{BC}\) 為左拐，這便是判斷 \(\overrightarrow{AB} \times \overrightarrow{BC} \ge 0\)，我們可以使用向量叉積來判斷。

以下為 C++ 求解凸包的代碼：

#include<bits/stdc++.h>
#define ll long long
#define inf (1ll << 62)
#define pb push_back
#define mp make_pair
#define PII pair<int , int>
#define fi first
#define se second
using namespace std;
struct Point {
	long double x , y , a;
};
vector<Point>pos;

inline long double dis(Point a , Point b) {//計算兩點距離
	return sqrtl((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

inline long double cross(Point a , Point b) {//計算向量叉積
	return a.x * b.y - b.x * a.y;
}

inline void solve() {
	int n;
	cin >> n;
	for(int i = 0;i < n;i ++) {
		long double x , y;
		cin >> x >> y;
		pos.pb({x , y , 0});
	}
	for(int i = 1;i < n;i ++) {//找出 y 坐標且 x 坐標最小的點
		if(pos[i].y < pos[0].y || (pos[i].y == pos[0].y && pos[i].x < pos[0].x)) {
			swap(pos[i] , pos[0]);
		} 
	}
	for(int i = 1;i < n;i ++) {//計算極角
		pos[i].a = atan2(pos[i].y - pos[0].y , pos[i].x - pos[0].x);
	}
	sort(pos.begin() + 1 , pos.end() , [](Point &x , Point &y) {//極角排序
		if(x.a == y.a) return dis(pos[0] , x) > dis(pos[0] , y);
		return x.a < y.a;
	});
	vector<int>st(n + 1);
	int top = 0;
	st[++ top] = 0;
	st[++ top] = 1;
	for(int i = 2;i < n;i ++) {//維護棧
		while(top >= 2 && cross({pos[st[top]].x - pos[st[top - 1]].x , pos[st[top]].y - pos[st[top - 1]].y} , {pos[i].x - pos[st[top]].x , pos[i].y - pos[st[top]].y}) < 0) top --;
		st[++ top] = i;
	}
	long double ans = 0;
    int last = 0;
	for(int i = top;i >= 1;i --) {//計算凸包周長
        ans += dis(pos[st[i]] , pos[last]);
        last = st[i];
    }
	cout << fixed << setprecision(2) << ans << "\n";
	return;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	int t = 1;
	// cin >> t;
	while(t --) {
		solve();
	}
	return 0;
}

二維凸包的應用

Graham 作為求解二維凸包的既經典、又高效的算法，在實際工程領域有著廣泛的應用。接下來我們將舉一個例子進行討論：

自動駕駛汽車

現在自動駕駛汽車的開發十分迅速，這與現代社會的科技的進步密不可分，但是我們不難從中看到一些二維凸包的影子。

比如，當自動駕駛汽車經過施工路段時顯然是需要識別路上的障礙標識的，并能在識別到行人時及時停下的。這怎么做到呢？我們可以在自動駕駛汽車車頭的方位放置攝像頭，然后當汽車遇到障礙物時攝像頭便可以對每個聚類出來的障礙物云簇（簇：指用來描述一組具有相似特征的數據點集合），然后將其投射到二維平面上使用 Graham 算法計算俯視圖的凸包。最終得到的凸多邊形便精確的描繪了障礙物在地面上的投射范圍。

所以，Graham 算法的存在，為現代科技發展提供了一定技術基礎。

三維凸包

三維凸包在現階段的主流做法主要為增量法，但能否有一種方法可以將 Graham 算法求解二維凸包的方法推廣到求解三維凸包呢？

我們考慮 Graham 算法能處理的問題的特點：在同一平面內。所以我們是否能夠在其中運用分治的思想，將求解三維凸包的過程拆解成求解數個二維凸包然和將這些二維凸包合并在一起呢？具體來說，就是優先枚舉在外圍的點，這可以通過排序實現，然后每次枚舉三個不共線點，求出其所在平面，然后枚舉其它點，判斷有多少個在該平面內，最后對所有在該平面內的點求解一遍二維凸包即可。

粗略的估算，時間復雜度是 \(O(n^4 \times n\log n)\) 的，\(n^4\) 為枚舉平面并判斷點是否在平面內的時間。這樣的時間復雜度是十分高的，算法效率很低，那有沒有什么優化的方法呢？注意到一個平面內可能有很多的點，所以這個平面就會被枚舉很多次，那是否可以令每個不同的平面只會被枚舉一次呢？我們可以對每個點維護一個集合 set，初始時每個點的集合包含整個點集，然后每次通過\(u_1\)、\(u_2\)、\(u_3\) 三點確定一個平面后再通過枚舉得出其它所在該平面的點集：\(A=\{u_1,u_2,u_3, u_4,\cdots, u_i\}\)。那么此時就對 \(A\) 中的每一個點的集合 \(U_i=\{u_1,u_2,u_3,u_4,\cdots, u_i\}\) 都將 \(u_1\)、\(u_2\)、\(u_3\) 刪去。最后對于每個點 \(u_i\) 我們只需要枚舉所在其集合中的點就可以避免重復枚舉平面。維護集合的時間復雜度是 \(O(\log n)\) 的，所以此時的總時間復雜度是：\(O(Vn\log n)\)，其中 \(V\) 為不同的平面的數量。

經過這樣子的一個優化，現在的這個算法在求解較為稀疏的三維凸包時已經能夠有了較好的表現，但實現的具體細節還需要具體的分析，就比如如何找到外圍的平面。如果想要更好的優化該算法的時間復雜度，那或許要等到未來進行進一步研究了。