開篇

??雖然所有的渲染在某種程度上都是“基于物理”的。但是在實踐中，“基于物理”意味著嚴格遵循物理模型，而不是“基于現象”，前者可以啟發式地捕捉主觀的感知特征，比如用經驗公式把高光放在“正確”的地方。這章覆蓋了基于物理的高級渲染，定義了領域中使用的單位和術語，此外還提供了一個可以非常緩慢地生成非常精確的圖像的蠻力“路徑追蹤”算法。在這里，我們不會深入許多渲染算法的細節，但是它們中的絕大多數都可以被看作是對蠻力算法的改進。

光子（Photons）

??為了幫助我們的直覺，我們將使用大量光子（Photon）的集合來描述輻射度量學。基于這個上下文，這個部分將建立對光子的認知。這里要注意，在圖形學中的“光子”和物理學中的不一樣，許多物理學家看到研究計算機圖形學的人寫的“光子追蹤”時會感到困惑。對于我們來說，光子只是一個能量包，它的行為遵循幾何光學（光以直線傳播而且沒有波屬性）。
??更加精確地說，光子對于我們來說是一束有位置、傳播方向、波長\(\lambda\)的光。波長的\(\mathrm{SI}\)的單位是納米（nanometer，nm）。一個光子也有著速度\(c\)只取決于傳播所在的介質的折射率\(n\)。有時頻率\(f=c/\lambda\)也會被使用。這很便捷因為不像\(\lambda\)和\(c\)，\(f\)在光子折射到一個新的介質時會保持不變。另一個不變的度量是光子攜帶的能量\(q\)，可以使用下方的公式求出。

式中的\(h=6.63 \times 10^{-34} \mathrm{J \, s}\)，它是普朗克常量。盡管這些量可以在任意單位系統下被測量，但是我們盡可能使用\(\mathrm{SI}\)單位。

光滑金屬（Smooth Metals）

??對于光滑金屬來說，光線要不被反射要不在折射后被金屬快速吸收。被反射的光的比例取決于菲涅爾方程（Fresnel Equations）。這些方程很簡單，但是很麻煩。此外，它們的值會隨著光的偏振變化，這在圖形學中通常被忽略。菲涅爾方程的主要視覺效果是反射率隨著入射角的增加而增加，特別是在掠射角附近時會接近\(100\%\)。
??幾乎所有的圖形程序都使用菲涅爾方程的一個簡單的近似，它由Schlick開發而來。對于金屬，我們通常指定法向反射率\(R_0(\lambda)\)。根據菲涅爾方程，反射率應該變化，Schlick開發的一個好的近似公式如下

其中\(\theta\)為光線入射方向和表面法線的夾角。在這里，近似值讓我們可以通過數據或人眼來設置金屬的法向反射率。

光滑電介質（Smooth Dielectrics）

??電介質是那些透明的并折射光的材料，皮膚、牛奶、頭發、衣物以及幾乎所有日常看到的物質都是電介質，盡管這可能不那么明顯，這是因為它們是有著不同折射率的吸光雜質的混合物。但是那些光滑均勻的電介質是透明的，比如玻璃、水、眼鏡鏡片。對于光滑電介質，有三個重要的屬性：

1. 對于每個入射角和波長，有多少光被折射。

2. 當光在物質中傳播時，對于給定的傳播距離和光的波長，光會衰減多少。

3. 被反射和折射的光的方向是什么。

電介質的反射率（Reflectivity of a Dielectric）

??光是如何彎曲以及有多少比例被反射/透射（折射）取決于物質的折射率\(n(\lambda)\)。對于電介質來說，可以使用相同的菲涅爾方程。但是如果另一個物質為空氣，我們可以根據\(n(\lambda)\)計算法向反射率\(R_0(\lambda)\)。

如果另一個物質的折射率不為\(1.0\)那么可以使用下方的公式

通常\(n\)不隨波長變化，但是在涉及色散的應用中，它會隨著波長變化。常用的折射率包括水（\(n=1.33\)）、玻璃（\(n=1.4\)到\(n=1.7\)）、鉆石（\(n=2.4\)）。那些被透射的為沒有被反射的那一部分，所以我們不需要顯式計算被透射的那一部分。

折射和比爾定律（Refraction and Beer's Law）

??電介質會過濾和折射光線，一些玻璃會過濾更多的紅光和藍光，因此呈現出綠色。當光從一個有著折射率\(n\)的介質傳播到一個新的有著\(n_t\)折射率的介質時，有些光會被透射也就是彎曲。下圖展示了\(n_t > n\)的一個情況

斯涅爾定律告訴我們

計算正弦值通常不如余弦值的計算方便，利用恒等式\(\sin^2\theta + \cos^2\theta =1\)，可以得到

這里要注意，如果\(n\)和\(n_t\)是顛倒的，那么\(\theta\)和\(\phi\)也得是，就如上方那張示例圖右邊展示的那樣。
??為了把\(\sin\phi\)和\(\cos\phi\)轉化為三維向量，我們可以在由表面法線\(\mathbf{n}\)和光線方向\(\mathbfw0obha2h00\)定義的平面上建立一個二維標準正交基。

從上圖我們可以知道透射方向\(\mathbf{t}\)用\(\mathbf{n}\)和\(\mathbf{b}\)這兩個基向量來表示為

我們可以使用相同的基向量來表示\(\mathbfw0obha2h00\)

既然已知\(\mathbfw0obha2h00\)，那么可以求出\(\mathbf{b}\)為

利用已知量，我們可以求得\(\mathbf{t}\)為

觀察這個公式你會想開方里的數如果小于\(0\)該怎么辦，在這種情況下，沒有被折射的光線，所有的光線都被反射了。這被稱為全內反射（Total Internal Reflection），它造就了玻璃物品的豐富外觀。
??對于均勻雜質，就像在典型的有色玻璃中發現的那樣，光線的強度會根據比爾定律（Beer's Law）衰減。當光線在介質中傳播時，它會根據\(dI=-CI dx\)來衰減強度，式中的\(dx\)為距離。因此，\(dI/dx=-CI\)。我們可以解這個式子得到\(I=k \mathrm{exp}(-Cx)\)。衰減的程度用RGB衰減常數\(a\)描述，它是單位距離的衰減量。加入邊界條件，我們知道\(I(0)=I_0\)和\(I(1)=aI(0)\)，前者意味著\(I(x)=I_0 \mathrm{exp}(-Cx)\)，后者意味著\(I_0a=I_0\mathrm{exp}(-C)\)，因此\(-C=\ln(a)\)。所以最終的公式為

式中的\(I(s)\)是光束在距離界面\(s\)處的強度。因為\(e^{\ln x} = x\)，這個公式也可以被寫作

在實踐中，我們通過眼睛逆向得出\(a\)，因為這種數據很難被找到。比爾定律的效果如下圖所示，在玻璃呈現綠色的地方。

??這種衰減的效果也適用于透射光，下圖展示了這些思想

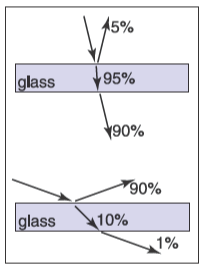
要注意的是，光會反復反射和折射，下方為一張示例圖

通常，只有一個或兩個反射成像是可見的。

有著次表面散射的電介質（Dielectrics with Subsurface Scattering）

??僅僅使用光滑電介質，我們可以渲染非常多的材料。那些看起來“啞光”和不透明的表面可以用多個電介質來模擬。比如一個完美的冰塊，它看上去和一塊玻璃一樣，只是有更低的折射率。現在在冰塊里放置很多小的球形空氣袋，隨著越來越多的空氣泡被添加，冰塊會變得越來越不透明。
??這種由空氣或其它物質形成的散射元素，造成了我們所見的大部分不透明性。另一種讓冰塊看起來不透明的方式是讓表面變粗糙。可以通過對表面進行鑲嵌細分，然后隨機地小幅度擾動頂點的位置做到。這會和磨砂玻璃的效果相似，擾動越粗糙，不透明度就越高。
??進一步的復雜性可以通過插入有顏色的粒子，從而激活比爾定律做到。這是一個相當簡單并且非常準確的用來模擬油漆的方法。
??有一些材料的復雜性可以用微觀結構的顯式建模來模擬。例如，人的皮膚可以被建模為一層粗糙的表面和幾層折射率略有不同的層，還有色素顆粒和血液。

一個蠻力的光子追蹤器（A Brute Force Photon Tracer）

??假設我們建模一個具有微觀結構電介質和一個發光物體的場景，我們怎么樣最簡單地渲染它并生成一張圖像呢？在這個部分，我們將會討論使用蠻力來模擬光子，以及如何從傳感器反向發出光子。在圖形學中，這確實可以生成一些最好的圖片，只需要寫一點代碼，但是速度會極慢。

傳感器（Sensor）

??為了生成一張圖像，我們必須對圖像捕獲設備有概念。一個簡單的可以是傳感器陣列和一個有著孔的盒子，就像針孔相機那樣。在陣列中的每個傳感器會本質上會充當一個光子計數器。被光子轟擊后，傳感器陣列會有值可以被寫入到圖像。那些接收到少量光子的傳感器將會寫入黑色，那些接收到大量光子的將會寫入白色，還有不同的灰度等級在這兩個之間。
??為了生成一張有顏色的圖像，我們可以按照特定的布局在傳感器前放置紅、綠、藍濾光片。最簡單的濾光片可以是帶通濾光片：

• \(\mathbf{藍光}\) 只在波長\(\lambda \in [400,500\,nm]\)內有全響應，其余無響應。

• \(\mathbf{綠光}\) 只在波長\(\lambda \in [500,600\,nm]\)內有全響應，其余無響應。

• \(\mathbf{紅光}\) 只在波長\(\lambda \in [600,700\,nm]\)內有全響應，其余無響應。

如果初始化傳感器為\(0\)，當光子通過濾光片擊中傳感器時，全響應只意味著存儲在傳感器上的數字會增加。

光子追蹤器（Photon Tracer）

??為了追蹤光子，可以取光源上的一個隨機點，然后取一隨機方向和一個在400到700納米之間的隨機波長。接著像第四章描述的那樣追蹤光線。當光線擊中一個表面時，計算它的反射率，然后決定是要反射還是折射。通過波長和入射角計算Schlick近似，我們稱之為\(R\)，接著再生成一個隨機數\(\xi \in [0,1)\)，于是我們能用如下的代碼進行決定。

如果表面為金屬，光在在折射之后會被直接吸收，我們可以從光源發出一條新的光線。
??如果光子進入電介質并且比爾定律系數不是\(1\)（意味著著電介質就像綠色玻璃那樣吸收光）時，那么光子有可能被吸收。我們可以使用相同的技巧在反射和折射之間進行決定。

上述的過程已經可以生成非常棒的圖像，但是速度會非常慢。

運動模糊和散焦模糊（Motion and Defocus Blur）

??上方描述的針孔相機將會生成銳利的圖像就像真實的針孔相機那樣。但是它需要長時間的曝光，因為只有少數光子有機會能通過針孔。
??我們可以為相機增加一個鏡片來讓針孔變大，即建模一系列真實的復合鏡片，或是直接插入一個理想的薄鏡片。最簡單的鏡片可以是兩個球的交點（“雙凸球面透鏡”）。它有非常好的成像性能而且很容易實現其與光相交的代碼。
??一個薄鏡片是理想化的無限薄的鏡片，而且只需要使用半徑和焦距\(f\)進行聲明。薄鏡片可以通過實現以下幾個屬性來實現，這些屬性為：

1. 一條從\(\mathbf{p}\)點離開并經過鏡片中心的光線不會被彎曲。

2. 所有離開\(\mathbf{p}\)點擊中鏡片的光線會匯聚到\(\mathbf{q}\)點。

3. 物體點\(\mathbf{p}\)沿著鏡片的光軸（Optical Axis）的距離\(a\)和成像點\(\mathbf{q}\)沿著光軸的距離\(b\)滿足：\(1/a+1/b=1/f\)。

下方為這三個屬性的一個示例圖

??這里要注意，擁有一個真實或理想的鏡片會自動得到真實照片中的那種模糊，它通常被稱為散焦模糊（Defocus Blur）或景深（Depth of Field）。
??為了得到運動模糊（Motion Blur），也就是運動的物體在照片中的模糊，或者相機在移動時讓那些速度和相機不一樣的物體變模糊。如果我們支持以下兩個特性，那么就能自動得到它，這兩個特性分別為：

• 光子在相機記錄的時間間隔中會在隨機時間從光源發出。

• 光線追蹤器有移動物體的概念，也就是光線相交代碼會以時間為參數。

一個簡單的移動的物體可以是一個球，它的中心在直線上隨時間變化，即

逆轉時間（Reversing Time）

??上方的光子追蹤器會良好地工作，但是還是會非常慢，因為即便是加了鏡片，大多數光子也不會擊中鏡片。有時在計算機圖形學中會逆轉時間，即從相機發射光線，記錄那些擊中光源的光線。我們為每個像素發出光子，看它們在哪擊中了光源。這些光子的波長是通過把顏色濾光片當作發光曲線決定的，當擊中了光源時，我們記錄光子，并給它一個權重。

輻射度量學（Radiometry）

??上個部分提到的蠻力渲染器在實踐中是不可行的。因此，與其建模微觀幾何，不如建模大量的行為。這是通過使用測量光的實際問題的工具完成的，通常被稱作輻射度量學（Radiometry）。在輻射度量學中出現的術語以及符號可能看起來有點怪。在這個部分最重要的量是輻亮度（Radiance），大多數學習計算機圖形學的人會把它映射到亮度、顏色、強度這種直觀的概念，而在實踐中,在\(99\%\)的情況下這么理解都是對的。但是有時，需要它的明確定義。
??雖然我們可以在許多系統中定義輻射單位，但是我們將會使用\(\mathrm{SI}\)單位。熟悉的\(SI\)單位包括米和千克。光是能量的一種基本的傳播形式，因此使用的是焦耳。

光譜能量（Spectral Energy）

??如果我們有大量的光子，它們的總能量\(Q\)是每個光子的能量\(q_i\)的和。一個合理的問題是“能量是如何在波長上分布的？”。這個問題可以轉化為求\(dQ/d\lambda\)，但是我們一直以來把光子當作單獨的個體，因此求出來的結果要不是\(0\)要不非常大。有兩種方法來解決這個問題，第一個是假設\(\Delta\lambda\)很小，但是沒有小到光的量子性質發揮作用。第二個方法是假設光是連續體而不是一個個光子，在這種情況下可以用\(dQ/d\lambda\)求解。這兩種方法都是合理的，而且會導致相同的計算機制。
??\(Q_\lambda\)被稱為光譜能量，它是一種強度量（Intensive Quantity）而不是像能量、長度或質量那種廣延量（Extensive Quantity）。強度量可以被思考成密度函數，它會告訴我們廣延量在一個無限小的點上的密度。例如，能量\(Q\)在某個波長可能是\(0\)，但是光譜能量\(Q_\lambda\)是有意義的量。
??我們將遵循圖形學的慣例，在很多時候使用光譜能量，而不是能量。也就是拋棄下標\(\lambda\)，直接使用\(Q\)來表示光譜能量，使用小寫\(q\)來表示能量，因此\(Q = \Delta q / \Delta \lambda\)。

功率（Power）

??在很多情況下計算光源的能量發生率是有用的，這被稱為功率，它是以瓦特測量的，也就是焦耳每秒。在穩定的狀態下很容易理解它，但是由于功率是強度量，當能量的發生率隨時間變化時也有明確的定義。
??和能量一樣，我們也對光譜功率（\(\mathrm{W(nm)}^{-1}\)）感興趣。標準的光譜功率符號是\(\Phi_\lambda\)，我們將直接使用\(\Phi\)。和光譜能量一樣的求法，光譜功率實際上就是小份光譜能量\(\Delta Q\)除以短時間\(\Delta t\)，即\(\Phi = \Delta q /(\Delta t \Delta \lambda)\)。

輻照度（Irradiance）

??當你想問“短時間\(\Delta t\)內有多少光擊中了這個點？”時，輻照度（Irradiance）會自然而然出現。當然了，答案是“沒有”，反而應該問短時間\(\Delta t\)內有多少光擊中了表面。而表面短時間內接收到的光應該是光源輻射到表面上的功率\(\Phi\)乘以時間\(\Delta t\)，因此“短時間\(\Delta t\)內有多少光擊中了這個點？”實際上求的是能量密度。把能量密度除以時間就有了我們的輻照度，假設表面上的小份面積為\(\Delta A\)，那么輻照度\(H\)為

可以把它理解為單位時間單位面積內的光擊中量。當光離開表面某點時，例如被反射時，我們可以把那部分光“收集”起來，“收集”起來的量被稱為輻射出射度（Radiant Exitance），我們用\(E\)來表示它。

輻亮度（Radiance）

??聰明的你可能想到了，表面上每個點接收到的輻照度實際上是由擊中這個點的所有光線貢獻的，因此是個積分過程！所以輻亮度（Radiance）就在這里出現了，假設一份小的立體角為\(\Delta \sigma\)，那么我們能求出\(\Delta H/\Delta \sigma\)。你可能會認為\(\Delta H/\Delta \sigma\)就是輻亮度，但是這是不對的，因為\(\Delta H/\Delta \sigma\)還和入射角有關。如果輻亮度的入射角\(\theta\)越大，那么它對輻照度的貢獻就越小，事實證明各個方向入射的輻亮度對輻照度的貢獻和\(\cos\theta\)線性相關。令輻亮度為\(L\)，那么有\(L \cos\theta = \Delta H/\Delta \sigma\)，因此輻亮度\(L = \Delta H/(\Delta \sigma \cos\theta)\)，即

和輻照度和輻射出射度一樣，我們應該區分入射于表面某點的輻亮度和離開表面某點的輻亮度。在圖形領域我們稱離開表面某點的輻亮度為表面輻亮度（Surface Radiance），一般用\(L_s\)來表示。而對于入射表面某點的輻亮度，我們稱為場輻亮度（Field Radiance），一般用\(L_f\)來表示。
??之前提到過表面上每點接收到的輻照度實際上是由擊中這個點的所有光線貢獻的，那么輻照度\(H\)就有如下的積分公式

式中的\(\mathbf{k}\)為入射方向。

散射的輻射度量學（Radiometry of Scattering）

??之前的光子追蹤假設表面上與光線交互的地方都是光滑的，在這里我們假設有潛在的復雜幾何體，這種幾何體有著精細的幾何細節。在實踐中，一個區域的大量屬性會被平均化來讓這個區域表現得像精細的幾何體那樣，從而無需存儲非常多的屬性。這個部分最重要的概念就是，對于粗糙表面，與其使用實際的幾何來表示所有小的劃痕，不如統計地描述劃痕，讓光滑的表面隨機向多個方向反射光線，就好像在表面上有許多不可見的小細節一樣。這個函數被稱為雙向反射分布函數（Bidirectional Reflectance Distribution Function，BRDF）。

BRDF

??因為我們對表面的外表感興趣，因此要描述表面是如何反射光的。在直覺層面上，任何從\(\mathbf{k}_i\)方向入射的光都有一部分會被散射到\(\mathbf{k}_o\)出射方向的一個小立體角區域。于是我們可以向下方那樣進行測量，把小的光源放到\(\mathbf{k}_i\)方向，把測量儀放到\(\mathbf{k}_o\)方向，對于每一對\((\mathbf{k}_i,\mathbf{k}_o)\)，我們取測量儀的讀數進行計算。

此外我們還要在被測量的點放置另一個輻照度測量儀來獲取光源的強度，因此反射率為

比例\(\rho\)會隨著入射方向\(\mathbf{k}_i\)和出射方向\(\mathbf{k}_o\)變化，如果我們對所有可能的方向進行測量，那么最終會得到一個四維函數\(\rho(\mathbf{k}_i,\mathbf{k}_o)\)。這個函數被稱為雙向反射分布函數（BRDF），我們只需要知道這個函數就能描述表面反射光線的方向屬性。

方向-半球反射率（Directional Hemispherical Reflectance）

??給定一個BRDF，我們就能直接問“入射光有多少比例被反射了？”。然而答案并不簡單，被反射的比例還取決于入射光的方向分布。正因為這樣，我們可以固定光線入射方向，計算輻射出射度占輻照度的比例。這個比例被稱為方向-半球反射率（Directional Hemisphere Reflectance），我們稱之為\(R(\mathbf{k}_i)\)，它是通過如下的公式定義的

對于給定的輻照度\(H\)，從BRDF的定義我們能知道方向\(\mathbf{k}_o\)上的表面輻亮度的計算公式為

此外，通過輻亮度的定義，我們也有

整理一下就能得到

為了得到\(R(\mathbf{k}_i)\)，我們對所有的出射方向\(\mathbf{k}_o\)進行積分

理想漫反射BRDF（Ideal Diffuse BRDF）

??一個理想的漫反射表面被稱作朗伯表面（Lambertian Surface），這種表面會向四周均勻散射入射的光線，也就是說朗伯表面的BRDF為常量。當常量為\(C\)時，如果我們要為這個表面計算\(R(\mathbf{k}_i)\)，那么有

傳輸方程（Transport Equation）

??利用BRDF，我們能根據不同方向上的入射輻亮度計算表面的輻亮度。取一小份立體角\(\Delta \sigma_i\)，可以知道入射方向\(\mathbf{k}_i\)小范圍內的輻亮度對表面上某點的輻照度的貢獻\(H=L_i\cos\theta_i\Delta\sigma_i\)。在這種情況下，BRDF為

因此我們能求得入射方向\(\mathbf{k}_i\)小范圍內的輻亮度對出射方向\(\mathbf{k}_o\)的輻亮度的貢獻

有了這個，我們能計算所有方向上的輻亮度對出射方向\(\mathbf{k}_o\)的輻亮度的貢獻

它在計算機圖形學中通常被稱為渲染方程（Rendering Equation）。有時，場輻亮度\(L_f(\mathbf{k}_i)\)可能來自環境中別的表面，就像下圖展示的那樣（\(L_f(\mathbf{k}_i)=L_s(-\mathbf{k}_i)\)）。

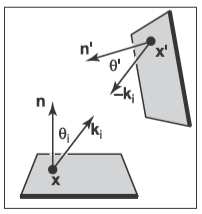
圖中點\(\mathbf{x}^\prime\)對應的立體角公式為

式中的\(\Delta A^\prime\)是與\(\mathbf{x}^\prime\)相關聯的面積，把\(\Delta\sigma_i\)替換成\(\Delta A^\prime\)可以得到下方的傳輸方程。

要注意的是，我們使用了非歸一化的向量\(\mathbf{x-x}^\prime\)來表示從\(\mathbf{x}^\prime\)到\(\mathbf{x}\)的方向。此外還要注意我們把\(L_s\)寫成了位置和方向的函數。
??上方積分公式的唯一問題就是積分域看起來怪怪的。如果我們能引入一個可見度函數，那么就能在積分域的復雜度和被積函數的復雜度之間權衡。

蒙特卡洛光線追蹤（Monte Carlo Ray Tracing）

??一旦我們使用積分來表達光照計算，那么我們就能使用蒙特卡洛積分來解決它。回想之前對它的描述，蒙特卡洛積分只是許多隨機樣本的平均值。在光線追蹤的情況下，就是為每個像素發出隨機光線，模擬其與環境的交互，最終計算出一些輻亮度，把平均輻亮度（顏色）寫入圖像我們就得到了使用蒙特卡洛光線追蹤計算出的圖像。具體怎么做可以看看下方提供的偽代碼

上述代碼描述了為每個像素發出光線，如果沒擊中物體那么返回環境顏色，如果擊中了物體那么就計算直接光照也就是光源的貢獻，此外還要加上周圍的物體對被擊中物體的貢獻，這正是因為

為了計算周圍物體對被擊中物體的貢獻，我們應該先從擊中點發射次級光線找到周圍的物體，可以像之前提供的代碼那樣調用函數本身。次級光線擊中周圍物體后，我們就能計算周圍物體對被擊中物體的貢獻。稍微想一想就會發現，這實際上是另外一些傳輸方程的積分過程，涉及到發射更低一級的光線。這個過程可以一直進行下去，直到所有光線未擊中場景中的物體，返回一個背景顏色。因此蒙特卡洛光線追蹤實際上是個遞歸的積分過程，它模擬的就是現實世界中，從光源出發的光線進入眼睛的逆過程。我們要做的就是不斷發出隨機光線，讓光線在物體之間彈射，只要發出的光線數量夠多，求出的平均顏色就能逼近真實值。

小節

??我滴個媽呀，居然真的寫完了。好像花了我45天還多，終于在暑假結束前一天寫完了。這下終于可以長嘆一口氣了，這真得休息一下吧。但是接下來，我想在這個部分總結下。
??第一當然是關于收獲。翻譯完這些重要的章節后，我感覺收獲是真的多呀！通過翻譯，我發現有一些地方我理解錯了，然后還看懂了一些原先不懂的內容，此外對書本知識的掌握也更扎實了。看來讀書真的是不止要讀，還要理解并記錄知識。真的是不積跬步無以至千里，不積小流無以成江河。
??第二是關于這本書。一直到基于物理的渲染的十幾章感覺還是不錯的，我感覺教了很多有用的知識，比如光線追蹤、光柵化、圖形管線什么的。不過后面的某些章節是真的拉跨，就比如接下來的曲線章節，感覺真的好垃圾，說了半天p話就講了那么一點知識，真是服了，我在圖書館都看急眼了。而且這章還有好多晦澀的知識，比如\(\mathrm{NURBS}\)，作者好像也沒怎么解釋。除了這個之外，后面的有些章節的一些地方我也看不太懂，特別是隱式建模（Implicit Modeling）這一章，讀的我懷疑人生了。應該是自己能力不太行，只能把能掌握的抓牢了。
??第三就是關于寫作能力。我發現我的表達能力是真的不行，感覺腦袋相關些地方真的是生銹了，有些地方感覺實在是太難翻譯了就借助了ChatGPT和有道。不過這也和沒時間有關，主要是這次給自己下了死命令必須暑假結束前寫完。暑假放松了好久，一時沒緩過來，結果只有20多來天時才開始寫，于是在某些地方用了ChatGPT和有道。我感覺這樣不行，以后應該多靠自己，所以真得猛猛寫文章，還要多推敲怎么寫，讓自己的死腦轉起來。不過這次翻譯完，感覺寫作能力還是提升了不少，明顯感覺后面翻譯的比前面好。后面得抽點時間，修改一些我不滿意的地方。
??現在沒什么想說的了，此時此刻我只想附上一首詩：

《七律·長征》
紅軍不怕遠征難，萬水千山只等閑。
五嶺逶迤騰細浪，烏蒙磅礴走泥丸。
金沙水拍云崖暖，大渡橋橫鐵索寒。
更喜岷山千里雪，三軍過后盡開顏。