《Fundamentals of Computer Graphics》第十二章圖形數據結構

開篇

??某些數據結構經常在圖形應用中出現，也許是因為它們能處理一些底層的基本想法，例如表面、空間和場景結構。這章將探討圖形數據結構中一些不相關的而且很基礎的并且最實用的一些類別，這些類別主要有網格結構、空間數據結構、場景圖、分塊多維數組。
??對于網格來說，我們將討論一些基礎的存儲方案，用于存儲靜態網格或是將網格傳輸到圖形API。我們也會討論翼邊數據結構和與之相關的半邊數據結構，這兩個數據結構能很好地管理鑲嵌細分變化的模型，例如細分或模型簡化的時候。盡管這些方法泛化到了任意的多邊形網格，但我們還是聚焦于三角形網格這種情況下。
??接下來，將會介紹場景圖數據結構，這種數據結構的多種形式在圖形應用中無處不在，就是因為它們在管理物體和變換上很有用。所有新的圖形API都被設計來支持場景圖。
??對于空間數據結構來說，我們會討論用來組織三維空間中的模型的三種方法，這三種方法有包圍體層次結構、層次化空間劃分、均勻空間劃分，此外還會討論利用層次化空間劃分（BSP樹）來移除隱藏表面，相同的方法也被用于不同的目的，包括幾何剔除和碰撞檢測。
??最后，將會介紹分塊多維數組，它一開始被開發是用來提高需要從磁盤換入圖形數據的應用的分頁性能，而現在，不管數組是否能放入主存儲器，這種結構對于機器上的內存局部性至關重要。

三角形網格（Triangle Meshes）

??絕大多數現實世界的模型都是由有著共享頂點的三角形構成的，這些通常被稱為三角網格（Triangular Meshes）或不規則三角形網（Triangular Irregular Networks，TINs），有效地處理它們對于圖形程序的性能至關重要。網格都是存儲在磁盤和內存中的，我們應該最小化存儲空間的消耗。當網格在網絡中或是從CPU到圖形系統傳輸時，它們會消耗帶寬，這通常比存儲更寶貴。在那些對網格操作的應用中，除了存儲還有繪制它們之外，還有細分、網格編輯、網格壓縮等等操作，對于這些操作來說，高效地獲取鄰接信息至關重要。
??三角形網格通常被用來表示表面，因此網格不是一些相互之間無關的三角形的集合，而是通過共享頂點和共享邊相互之間連接的三角形網絡，這些三角形一起形成了一個單獨的連續表面。這是對網格的一個關鍵的洞悉，相比于相同數量的無關的三角形的集合，一個網格可以被更加有效率地處理。
??一個三角網格需要的最小信息是一系列三角形以及它們的頂點的位置。在一些情況下，程序需要在頂點、邊或面存儲額外的信息來支持紋理映射、著色、動畫以及其它操作。其中頂點數據是最常見的，每個頂點可以擁有材質參數、紋理坐標、輻照度以及任何在表面上改變的值。這些參數會在每個三角形上被線性插值從而定義了一個在網格的整個表面上的連續函數。然而，存儲每條邊和每個面的數據有時也很重要。

網格拓撲（Mesh Topology）

??網格是類表面這一想法可以形式化為對網格拓撲的一些約束，也就是不管頂點的位置，對于三角形之間的連接方式的約束。許多算法只會或更容易在網格有可預測的連接性的情況下實現。最簡單的也是最有限制的對于網格拓撲的要求是表面應該是流形（Manifold）。一個流形網格應該是“防水的”，也就是沒有間隙并把空間分成了表面內部和表面外部。它看起來也像網格上的一個表面。
??流形這個術語來自拓撲的數學領域，大致上講，一個流形（特別是二維流形）是一個表面，在這個表面上的點和它周圍的點只能組成一個比較平坦的表面。接下來讓我們看個例子，下方是一張示例圖

觀察一下，很容易發現左邊是非流形，因為上下金字塔相接的點與它周圍的點可以形成多個表面。許多算法會假設網格是流形，因此應該驗證這一屬性來避免崩潰或無限循環。這個驗證可以歸結為通過下面的條件來檢查所有邊和所有頂點是否都是流形。

每條邊都正好被兩個三角形共享
每個頂點周圍只有一個三角形循環

之前那張示例圖就展示了，有太多的三角形循環從而驗證失敗。下面這張示例圖展示了一條邊被太多的三角形共享而驗證失敗。

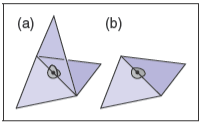
??流形網格很便捷，但是有時應該允許網格有邊界。對于一個有著邊界的流形我們可以放寬流形網格的要求，放寬后的條件為

每條邊被一個或兩個三角形使用
每個頂點連接著一個邊與邊相接的三角形的集合

下方的一張示例圖展示了這些條件

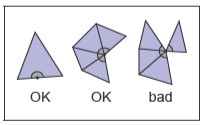
??最后，在許多應用中能夠把表面的“前面”或“外面”和表面的“背面”或“里面”區分開來很重要，這被稱為表面的朝向（Orientation）。對于一個單獨的三角形，我們基于頂點被列出的順序來定義朝向，正面是按逆時針順序排列的時候。在一個連通的網格中，如果它的三角形都同意哪一邊是正面，那么它的朝向是固定的。
??在一對有一致朝向的三角形中，兩個共享的頂點在兩個三角形的頂點列表中會以相反的順序出現，就如下圖展示的那樣。對于一致朝向重要的是，有些系統會使用順時針來定義正面而不是逆時針。

??任何有著非流形邊的網格不可能有一致的朝向。對于一個有著邊界的流形來說也可能會這樣，這種是不可定向的表面，就如下圖展示的莫比烏斯帶的例子。

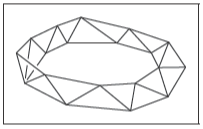
索引化網格存儲（Indexed Mesh Storage）

??一個簡單的三角網格如下圖所示

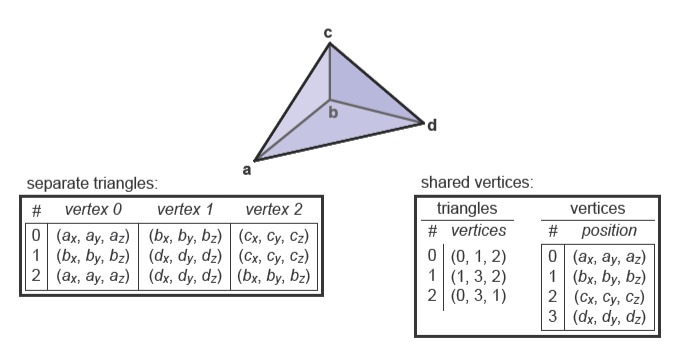
我們可以像下面這樣存儲每個三角形

Triangle
{
    vector3 vertexPosition[3]
}

不過這樣會導致圖中的\(\mathbf{b}\)頂點存儲三次和其它頂點存儲兩次。實際上可以采用共享的方式存儲四個頂點，這樣就有了一個共享頂點的網格（Shared-vertex Mesh）。

Triangle
{
    Vertex v[3]
}

Vertex
{
    vector3 position
    //其它頂點數據
}

要注意的是這里的Vertex v[3]只是頂點對象的引用或指針。在實踐中，頂點和三角形通常是存儲在數組中的，我們可以使用索引來間接聲明三角形的頂點，因此可以使用索引數組來定義網格。

IndexedMesh
{
    int tInd[nt][3]
    vector3 verts[nv]
}

第\(i\)個三角形的第\(k\)個頂點會在頂點數組的第tInd[i][k]個位置，使用這種方法來存儲的共享頂點的網格叫索引化三角形網格（Indexed Triangle Mesh）。下方為一張索引化三角形網格的示例圖

??那么使用共享頂點有沒有空間優勢呢？如果我們有\(n_v\)個頂點和\(n_t\)個三角形，假設浮點、指針、整數都需要相同的存儲空間，那么空間需求有如下：

普通三角網格：每個三角形三個向量也就是\(9n_t\)單位大小。
索引化網格：每個頂點一個向量，每個三角形三個整數，也就是\(3n_v+3n_t\)單位大小。

??根據經驗來說，一個大的網格的每個頂點會連接約六個三角形。因為每個三角形連接三個頂點，這意味著三角形數量約為頂點數量的兩倍（\(n_t \approx 2 n_v\)）。那么不使用索引化網格需要\(18n_v\)單位，使用只需要\(9n_v\)單位，這樣就節省了一半的空間。

三角形條帶和三角形扇面（Triangle Strips and Fans）

??索引化網格是最常見的在內存中表示三角形網格的方式，因為它在簡單性、便捷性、緊湊性之間達到了良好的平衡。它也通常被用來在網絡中和從CPU到圖形系統的傳輸。在一些需要更緊湊性的應用中，三角形頂點的索引可以被更加效率地用三角形條帶（Triangle Strip）和三角形扇面（Triangle Fan）來表示。
??一個三角形扇面如下圖所示

在一個索引化網格中，三角形數組包含\([(0,1,2),(0,2,3),(0,3,4),(0,4,5)]\)，我們存儲了12個頂點索引，盡管只有6個不同的頂點。在一個三角形扇面中，所有的三角形共享一個頂點，上圖的扇面可以用\([0,1,2,3,4,5]\)來表示，第一個頂點為共享的頂點，它會與后續的每一對相鄰的頂點（1-2、2-3等等）創造一個三角形。
??三角形條帶是個相似的概念，不過更適用于更大范圍的網格。像下圖一樣，頂點被交替的在上下添加，構成了一個線性條帶。

上圖的條帶可以用\([0,1,2,3,4,5,6,7]\)來表達，序列中每三個相鄰的頂點（0-1-2、2-1-3等等）創造了一個三角形。對于一個新進入的頂點，最老的頂點會被拋棄，兩個剩下的頂點會交換順序。
??在條帶和扇面中，\(n+2\)個頂點就足夠描述\(n\)個三角形，相比于標準的索引化網格需要的的\(3n\)個頂點節省了很多。對于長三角形條帶來說，可以節省三倍。似乎三角形條帶只在條帶很長的時候有用，實際上對于相對短的條帶來說，已經能獲得非常大的提升，存儲空間的節省（只對于頂點索引）如下圖所示。

??因此，即使是一個非結構化的網格，使用一些貪心算法把它們聚集成短條也是值得的。

網格連接性的數據結構（Data Structures for Mesh Connectivity）

??索引化網格、條帶、扇面都是靜態網格的緊湊且良好的表示，然而它們不容易讓網格被修改。為了有效率地編輯網格，更加復雜的數據結構需要快速地回答下方的問題。

給定一個三角形，哪三個三角形與它相鄰？
給定一個邊，哪兩個三角形共享它？
給定一個頂點，哪些面共享它？
給定一個頂點，哪些邊共享它？

對于三角形網格、多邊形網格和有著孔洞的多邊形網格來說，有很多可用的數據結構。在許多應用中，網格會非常大，因此高效地表示至關重要。
??最直接也最臃腫的實現是使用三種類型Vertex、Edge、Triangle存儲所有的關系

Triangle
{
    Vertex v[3]
    Edge e[3]
}

Edge
{
    Vertex v[2]
    Triangle t[2]
}

Vertex
{
    Triangle t[]
    Edge e[]
}

這樣就能直接回答上面的問題，不過由于這些信息都是相互關聯的，因此存儲了一些多余的信息。此外，為每個頂點存儲連接信息會導致有可變長度的數據結構，這種實現起來效率較低。事實證明，我們可以只存儲部分連接信息，在需要的時候可以高效地恢復其它信息。
??固定大小的Edge和Triangle類明顯可以更有效率地存儲連接信息。事實上，在一個由有著任意數量的邊和頂點的多邊形組成的多邊形網格中，只有邊有著固定大小的連接信息，這就導致了有非常多的基于邊的傳統網格數據結構。但是對于只有三角形的網格來說，在面上存儲連接信息也是可以的。
??一個好的網格數據結構應該要足夠的緊湊，而且還要能高效地回答所有的鄰接查詢。這里的高效意味著常時間，也就是找到鄰居的時間不應該取決于網格的大小。接下來讓我們看看三種數據結構，一個基于三角形，另外兩個基于邊。

三角形鄰接結構（The Triangle-Neighbor Structure）

??我們以之前說的共享頂點的網格為基礎，為三角形類增加與它相鄰的三個三角形的指針，為頂點類增加任意一個包含它的三角形的指針，這樣就實現了一種緊湊的網格數據結構。

Triangle
{
    Triangle nbr[3]
    Vertex v[3]
}

Vertex
{
    Triangle t
}

下方為一張相關的示例圖

可以發現某個三角形和它的第\(k\)個鄰居共享它的第\(k\)和第\((k+1) \; \mathrm{mod} \; 3\)個頂點。我們稱這種結構為三角形鄰接結構（The Triangle-Neighbor Structure）。從標準的索引化網格開始，我們只需要增加兩個數組，一個用來存儲每個三角形的三個鄰居的索引，另一個用來存儲每個頂點的任意一個鄰居三角形的索引，就能實現三角形鄰接結構。

Mesh
{
    int tInd[nt][3]
    int tNbr[nt][3] //每個三角形的三個鄰居的索引
    int vTri[nv] //每個頂點的任意一個鄰居三角形的索引
}

這種結構能直接回答前兩個問題，對于后兩個問題我們得利用現有的信息來回答。回顧之前說的逆時針被列出為正面，以及某個三角形和它的第\(k\)個鄰居共享它的第\(k\)和第\((k+1) \; \mathrm{mod} \; 3\)個頂點這兩個條件，這個時候就發現了可以以順時針方向遍歷包含相同頂點的三角形，下面給出偽代碼

TrianglesOfVertex(v)
{
    t = v.t
    do
    {
        i = find (t.v[i] == v) //搜索得出v是t三角形的第幾個頂點
        t = t.nbr[i] //以順時針方向要遍歷的下一個三角形應該是t的第i個鄰居三角形
    } while (t != v.t)
}

下方為一張順時針遍歷的示例圖

這個操作會以常時間找到后續的三角形，然而進行搜索需要額外的分支。我們遇到的問題其實是移動到下一個三角形的時候，就不記得是從哪來了。為了解決這個問題，我們應該存儲和邊有關的信息。首先，對于任意一個三角形，我們首先應該知道與它的每個邊對應的鄰居三角形的指針，此外我們還需要知道它的每個邊在對應的鄰居三角形中的位置，這樣就能知道從哪里來。可以通過上方的示例圖來說明這一想法，假設現在在\(T_2\)三角形，要前往的下一個三角形是\(T_1\)，通過\(T_2\)邊上存儲的信息我們可以知道\(\mathbf{p}_2\mathbf{p}_3\)這條邊在三角形\(T_1\)中的位置，于是在到達\(T_1\)三角形后，直接訪問下一條邊也就是\(T_1\)三角形的\(\mathbf{p}_2\mathbf{p}_0\)邊上的數據，這樣就能直接知道下一個要去的是\(T_0\)三角形。因此有如下的數據結構

Triangle
{
    Edge nbr[3]
    Vertex v[3]
}

Edge
{
    Triangle t//與邊對應的鄰居三角形
    int i//這條邊在對應的鄰居三角形中的位置
}

Vertex
{
    Edge e//任意離開頂點的邊，如上圖的p2p0這種
}

在實踐中，Edge中的\(i\)會借用\(t\)兩比特位來確保存儲空間不變。循環遍歷算法為

TrianglesOfVertex(v)
{
    {t, i} = v.e
    do
    {
        {t, i} = t.nbr[i]
        i = (i + 1) mod 3
    } while (t != v.e.t)
}

??三角形鄰接結構是非常緊湊的，對于一個只有頂點位置的網格來說，每個頂點要4個數字，每個面要6個數字，每頂點約消耗\(4n_v+6n_t \approx 16n_v\)單位的空間，對于標準的索引化網格來說每頂點要\(9n_v\)。
??在這個部分呈現的三角形鄰接結構只對流形網格有用，因為使用的TrianglesOfVertex算法的返回取決于是否回到起點，對于有著邊界的流形來說，我們可以引入\(-1\)這樣的值，并讓邊界頂點指向最逆時針的鄰居三角形，而不是指向任何任意三角形。

翼邊結構（The Winged-Edge Structure）

??一個在邊上存儲連接信息并被廣泛使用的網格數據結構是翼邊（winged-edge）數據結構。在一個翼邊網格中，每個邊會存儲它連接的兩個頂點的指針，分別為頭指針和尾指針。此外還會存儲左右兩個面的指針和與它相連的四個邊的指針，這四個邊的指針分為\(\mathrm{ln}\)（Left Next）、\(\mathrm{rn}\)（Right Next）、\(\mathrm{lp}\)（Left Previous）、\(\mathrm{rp}\)（Right Previous）。這里要注意一點，在翼邊結構中，從上一個邊（Previous）到當前的邊再到下一個邊（Next）的環繞左右面的回路為逆時針。下方為兩張形象的示例圖

因此類的定義有如下

Edge
{
    Edge lprev, lnext, rprev, rnext
    Vertex head, tail
    Face left, right
}

Face
{
    Edge e//這個面包含的任意一條邊
}

Vertex
{
    Edge e//包含這個頂點的任意一條邊
}

翼邊數據結構支持常時間訪問一個面的邊和一個頂點的邊，有了之前提供的信息，很容易推導出遍歷頂點的所有邊以及遍歷面的所有邊的算法為

EdgesOfVertex(v)
{
    e = v.e
    do
    {
        if (e.tail == v)
            e = e.lprev
        else
            e = e.rprev
    } while (e != v.e)
}

EdgesOfFace(f)
{
    e = f.e
    do
    {
        if (e.left == f)
            e = e.lnext
        else
            e = e.rnext
    } while (e != f.e)
}

??這些相同的算法和數據結構可以在不止有三角形的多邊形網格中工作，這也是基于邊的結構的一個非常重要的優勢。和其它的數據結構一樣，翼邊數據結構可以做一些時間和空間上的衡量。比如，我們可以去除對\(\mathrm{prev}\)的引用，從而節省一定的空間，不過會導致環繞面順時針遍歷或環繞頂點逆時針遍歷變難，如果想知道上一個邊，那么得順著下一個邊的方向繞一大圈來得到。

半邊結構（The Half-Edge Structure）

??翼邊數據結構非常優雅，但是在環繞面或頂點遍歷時需要時刻檢查方向，這就像未被優化的TrianglesOfVertex算法那樣。因此，與其在每個邊上存儲數據，不如在每個半邊（half-edge）上存儲數據。背后的想法很簡單，即把每個邊分成朝向相反的一對半邊，并分配給共享這個邊的兩個三角形，要求是每個三角形的半邊要有一致的朝向。這樣看來每個半邊得存儲它所屬的面和它指向的頂點，除此之外為了方便遍歷還得存儲它對應的另一個反向半邊和它在所屬環路中的下一個半邊，當然了存儲它在環路中的上一個半邊也是可以的。下方為一張形象的示例圖

于是有如下的結構

HEdge
{
    Hedge pair, next
    Vertex v
    Face f
}

Face
{
    HEdge h//這個面包含的任意半邊
}

Vertex
{
    HEdge h//指向這個頂點的任意一個半邊
}

下面給出使用半邊數據結構環繞頂點和面遍歷的代碼

EdgesOfVertex(v)
{
    h = v.h
    do
    {
        h = h.pair.next
    } while (h != v.h)
}

EdgesOfFace(f)
{
    h = f.h
    do
    {
        h = h.next
    } while (h != f.h)
}

??半邊一般都是成對出現的，不過很多的實現不會顯式存儲\(\mathrm{pair}\)指針。例如在一個基于數組索引的實現中，偶數索引\(i\)的半邊與會與索引為\(i+1\)的半邊組成一對，奇數索引\(j\)的半邊會與索引為\(j-1\)的半邊組成一對。就像下圖展示的這樣

??除了這章展示的簡單遍歷算法外，這三種網格拓撲結構都支持不同類型的“網格手術”操作，比如拆分或合并頂點和邊交換，以及添加或刪除三角形。

場景圖（Scene Graphs）

??一個三角形網格管理著組合成一個物體的所有三角形的集合，但是在圖形應用中的另一個普遍的問題是把物體放到期望的位置。就如同我們在第七章看到的那樣，擺放物體是通過變換做到的，但是復雜的場景會包含非常多的變換，如果能把這些變換管理好，那么場景就更容易被操作。絕大多數場景都可以使用層次結構來組織，變換可以通過場景圖（Scene Graph）按照這種層次來管理。
??為了引出場景圖數據結構，我們首先看個鉸鏈擺的例子，下面是與之相關的示例圖

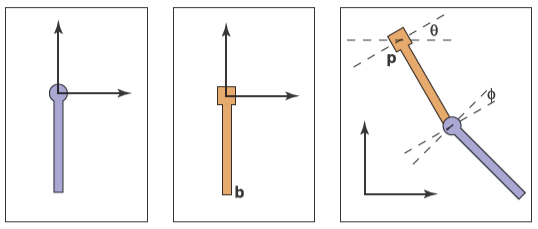
由圖可知對于上鐘擺的變換\(\mathbf{M}_3\)有

\[\begin{align*} \mathbf{M}_1 &= \mathrm{rotate}(\theta) \\ \mathbf{M}_2 &= \mathrm{translate}(\mathbf{p}) \\ \mathbf{M}_3 &= \mathbf{M}_2\mathbf{M}_1 \end{align*} \]

下鐘擺的變換會更復雜，但是我們能利用下鐘擺附著在上鐘擺的底部也就是局部坐標系中的\(\mathbf{b}\)點這一事實和上下鐘擺的旋轉角度差也就是上圖所示的相對角度\(\phi\)來進行疊加變換。在上鐘擺變換前我們先把下鐘擺旋轉一個相對角度\(\phi\)，然后把下鐘擺移動到上鐘擺的\(\mathbf{b}\)點位置，接著跟隨上鐘擺變換即可。使用數學語言來描述下鐘擺的變換矩陣\(\mathbf{M}_d\)則為

\[\begin{align*} \mathbf{M}_a &= \mathrm{rotate}(\phi) \\ \mathbf{M}_b &= \mathrm{translate}(\mathbf{b}) \\ \mathbf{M}_c &= \mathbf{M}_b\mathbf{M}_a \\ \mathbf{M}_d &= \mathbf{M}_3\mathbf{M}_c \end{align*} \]

這說明下鐘擺的坐標系實際上在跟隨上鐘擺移動，因此我們能使用一種數據結構來更好地管理這些坐標系的問題，就如同下圖展示的這樣

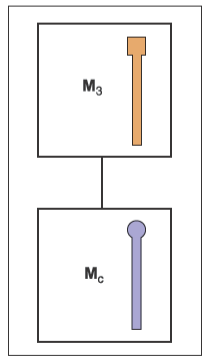
通過利用這種數據結構，我們能得到對于一個物體施加的變換只是從數據結構的根到物體的鏈條涉及到的所有矩陣的乘積。假設有一個搭載著車輛的渡輪，車可以自由地在甲板上移動，車輪會相對于車移動，于是有如下的數據結構

和鐘擺一樣，每個物體的變換應該是從根到物體的路徑涉及到的所有矩陣的乘積，于是有

渡輪的變換使用為\(\mathbf{M}_0\)
車身的變換使用為\(\mathbf{M}_0\mathbf{M}_1\)
左邊的輪子使用的變換為\(\mathbf{M}_0\mathbf{M}_1\mathbf{M}_2\)
右邊的輪子使用的變換為\(\mathbf{M}_0\mathbf{M}_1\mathbf{M}_3\)

在光柵化中（In rasterization）

??在光柵化中一個高效的實現是矩陣棧（Matrix Stack），這種數據結構被許多的API支持。一個矩陣棧可以通過入棧（Push）和出棧（Pop）來操作，它們實現的是從右側增加和刪除矩陣，比如可以調用

\[\begin{align*} &\mathrm{push}(\mathbf{M}_0) \\ &\mathrm{push}(\mathbf{M}_1) \\ &\mathrm{push}(\mathbf{M}_2) \end{align*} \]

得到活動矩陣\(\mathbf{M}=\mathbf{M}_0\mathbf{M}_1\mathbf{M}_2\)，接著調用\(\mathrm{pop}()\)刪除最后一個矩陣，于是活動矩陣變成了\(\mathbf{M}=\mathbf{M}_0\mathbf{M}_1\)。把矩陣棧與場景圖結合起來，可以得到使用先序遍歷來繪制所有物體的算法

場景圖有非常多的變種，不過它們都支持上面這種基本的想法。

在光線追蹤中（In ray tracing）

??光線追蹤的一個優雅性質是，它允許非常自然的變換應用，而不需要改變幾何表示。實例化的基本想法是在顯示物體前通過變換矩陣來扭曲物體上的所有點，就如下圖所示的那樣

使實體稱為“實例”的關鍵是存儲基物體和對應的復合變換矩陣，不過在渲染的時候一般需要顯式地構造變換后的幾何體。但是在光線追蹤中使用實例化有個優勢，假如有個基物體，它的一個實例會使用\(\mathbf{M}\)來變換，如果求得的交點為\(\mathbf{P}\)，那么有

\[\mathbf{a} + t \mathbf{b} = \mathbf{P} \]

由于實例是通過矩陣\(\mathbf{M}\)變換的，于是可以在兩邊乘以矩陣的逆，因此有

\[\mathbf{M}^{-1}\mathbf{a} + t \mathbf{M}^{-1}\mathbf{b} = \mathbf{M}^{-1} \mathbf{P} \]

因為\(\mathbf{M}^{-1} \mathbf{P}\)是基物體上的點，因此我們也可以求被逆變換的光線與基物體的交點。這么做的兩個潛在的好處如下：

基物體可能有更簡單的求交流程。
許多變換后的物體可以共享相同的基物體，因此能節省存儲空間。

??這里有個問題要注意，在基物體空間中求交所得到的法線必須被變換到世界空間中，由于實例是用\(\mathbf{M}\)矩陣進行變換的，因此在基物體空間中求交得到的法線\(\mathbf{n}\)得用\((\mathbf{M}^{-1})^\mathrm{T}\)來變換。下面給出實例與光線求交的代碼。

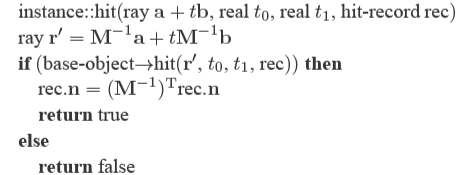
這個代碼的一個優雅的地方是參數\(\mathrm{rec}.t\)不需要被修改，因為它和求交所在的空間無關。此外也不需要計算或存儲矩陣\(\mathbf{M}\)，只需要它的逆\(\mathbf{M}^{-1}\)。關于上面的代碼其實還能有新的認知，那就是不應該限制光線方向\(\mathbf{b}\)為單位向量，如果這樣做會導致很多問題，比如無法求出正確的參數\(\mathrm{rec}.t\)。下方為一張在基物體空間中求交和在世界空間中求交的示例圖。

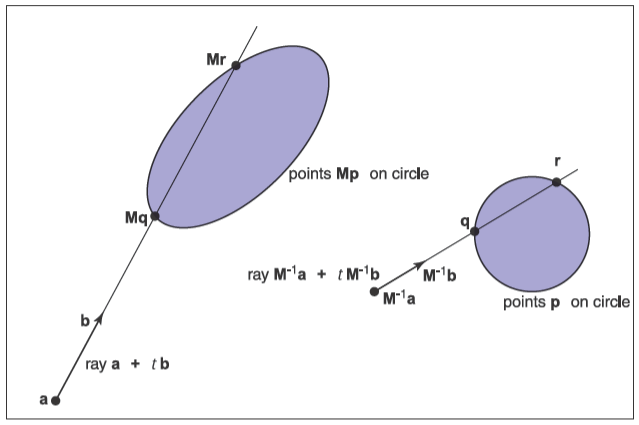
空間數據結構（Spatial Data Structure）

??在很多圖形應用中，在特定的區域快速定位幾何物體的能力非常重要。光線追蹤器需要找到與光線相交的物體，在環境中進行導航的交互式應用需要找到任意視點下可見的物體，游戲以及物理模擬需要檢測物體什么時候以及在哪碰撞。這些所有的需求可以通過使用各種各樣的空間數據結構來滿足，它們可以組織空間中的物體，來讓查找更加高效。
??這個部分將討論三種一般類型的空間數據結構的例子。能將物體組合到一個層次的結構為物體劃分結構（Object Partitioning Schemes），雖然物體在這個結構中被分到了不相交的組，但是這些組可能在空間中有重疊。能將空間劃分到不相交的區域的結構為空間劃分結構（Space Partitionning Schemes），劃分可以是規則或不規則的。在規則劃分的情況下，空間會被劃分為一些形狀和大小一致的區域。在不規則劃分的情況下，空間會被適應性地劃分為一些不規則的區域，在更小區域內會有更多更小的物體。
??討論這些結構時將使用光線追蹤來說明，盡管它們也能被用于視錐體剔除和碰撞檢測。在第四章中，當需要檢測相交時，我們會遍歷空間中的所有物體，這就導致了一個時間復雜度為\(O(N)\)的線性搜索，對于大型場景來說會很慢。和大多數的搜索問題一樣，只要我們能預先創建一個有序的數據結構，那么光線與物體的交匯可以使用分而治之的技術，在次線性時間內完成計算。
??下面的部分將詳細地討論這些技術，這些技術主要有包圍體層次結構（Bounding Volume Herarchies）、均勻空間劃分（Uniform Spatial Subdivision）、二叉空間劃分（Binary Space Partition）。下面的一張示例圖展示了前兩個技術的例子。

包圍盒（Bounding Boxes）

??對于加速交匯檢測的一個關鍵操作是計算光線是否與包圍盒相交，就如下圖那樣。

如果光線不與包圍盒相交，那么就不需要檢測光線與包圍盒中的幾何體是否相交。為了建立一個光線與盒相交的算法，我們可以先考慮二維的情況，后續可以推廣到三維。我們使用兩個水平直線和兩個垂直直線來定義二維包圍盒，于是有

\[\begin{align*} x &= x_\mathrm{min} \\ x &= x_\mathrm{max} \\ y &= y_\mathrm{min} \\ y &= y_\mathrm{max} \\ \end{align*} \]

那么被這個包圍盒包圍的點為

\[(x,y) \in [x_\mathrm{min},x_\mathrm{max}] \times [y_\mathrm{min},y_\mathrm{max}] \]

由于只要確定是否相交而不是求交點，我們能采用一個更快的方法。首先先計算光線與水平直線的兩個交點的參數\(t\)，于是有

\[t_\mathrm{xmin} = (x_\mathrm{min}-x_e)/x_d \]

\[t_\mathrm{xmax} = (x_\mathrm{max}-x_e)/x_d \]

計算出來參數后，我們能得到一個區間\([t_\mathrm{xmin},t_\mathrm{xmax}]\)。對于垂直直線的情況，我們如法炮制，得到另一個區間\([t_\mathrm{ymin},t_\mathrm{ymax}]\)。接下來需要判斷這兩個區間是否重疊，如果重疊，那么意味著光線上有點在包圍盒內，也就意味著光線和包圍盒相交，反之則不相交。因此算法的偽代碼為

t_xmin = (x_min - x_e) / x_d
t_xmax = (x_max - x_e) / x_d
t_ymin = (y_min - y_e) / y_d
t_ymax = (y_max - y_e) / y_d

if (t_xmin > t_ymax) or (t_ymin > t_xmax)
    return false
else
    return true

這里有些地方要注意，首先\(x_d\)或\(y_d\)可能是負的。如果\(x_d\)是負的，那么得交換下順序，于是有

if (x_d >= 0)
    t_xmin = (x_min - x_e) / x_d
    t_xmax = (x_max - x_e) / x_d
else
    t_xmin = (x_max - x_e) / x_d
    t_xmax = (x_min - x_e) / x_d

其次還要注意\(x_d\)或\(y_d\)為\(0\)的情況，回顧第一章提到的的IEEE浮點數模型，里面提到對于任意正實數\(a\)有

\[+a/0 = +\infty \\ -a/0 = -\infty \]

當\(x_d=0\)時，有

\[t_\mathrm{xmin} = \frac{x_\mathrm{min}-x_e}{0} \]

\[t_\mathrm{xmax} = \frac{x_\mathrm{max}-x_e}{0} \]

于是有以下三種情況需要考慮

\(x_e \leq x_\mathrm{min}\)
\(x_\mathrm{min} < x_e < x_\mathrm{max}\)
\(x_\mathrm{max} \leq x_e\)

對于第一種情況，我們能得到區間\((t_\mathrm{xmin},t_\mathrm{xmax})=(\infty,\infty)\)，這個區間不會與任意的區間重疊，因此不會相交，這是我們期望的一個結果。對于第二種情況我們能得到區間\((t_\mathrm{xmin},t_\mathrm{xmax})=(-\infty,\infty)\)，這個區間會與任意區間重疊，因此會有相交，這也是我們期望的一個結果。第三種情況和第一種一樣不會有相交。因此對于以上這些情況我們能信任IEEE浮點數模型，不過還有最后一個問題要注意，假如我們使用

if (x_d >= 0)
    t_xmin = (x_min - x_e) / x_d
    t_xmax = (x_max - x_e) / x_d
else
    t_xmin = (x_max - x_e) / x_d
    t_xmax = (x_min - x_e) / x_d

當\(x_d=-0\)時又會出問題，解決方法也很簡單，就是使用\(x_d\)的倒數進行計算，因此有

a = 1 / x_d
if (a >= 0)
    t_xmin = a*(x_min - x_e)
    t_xmax = a*(x_max - x_e)
else
    t_xmin = a*(x_max - x_e)
    t_xmax = a*(x_min - x_e)

層次包圍盒（Hierarchical Bounding Boxes）

??層次包圍盒的基本想法是使用軸對齊的包圍盒來包圍所有物體。雖然光線與包圍盒的相交計算有開銷，但是一旦光線未命中包圍盒，那么就能減少大量的相交檢測。使用更大的包圍盒來包圍小的包圍盒就形成了層次結構，一張相關的示例圖如下

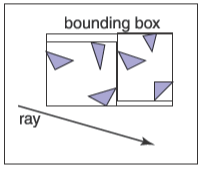
而與之相關的一張可能的數據結構的示例圖如下

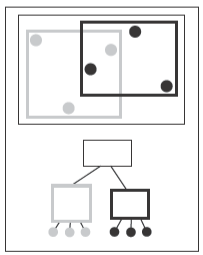
為了計算光線與物體的交點，我們必須遍歷樹中的節點，于是有如下的算法

觀察這個算法你會發現子樹之間沒有幾何順序，也就是說光線可能會同時擊中兩個子樹。這是因為包圍盒只會保證包圍在它層次之下的所有物體，而不會保證包圍盒之間在空間中不重疊，就如之前所展示的數據結構的示例圖那樣。這就導致了這種幾何搜索會比傳統的二叉搜索要復雜，對于這種情況你可能想到了一些可能的優化方法，等我們有一個完整的層次算法時再來想它。
??如果我們限制樹為二叉的并且要求樹中的每個節點都有一個包圍盒，那么遍歷代碼可以自然地展開。除此之外，假設每個葉子節點包含一個圖元，每個非葉子節點包含一個或兩個子樹。
??bvh-node類應該是表面類的子類，因此它應該實現surface::hit。它包含的數據應該很簡單，于是有

遍歷的代碼可以使用遞歸來實現，因此有

??有許多方式來建立包圍體層次結構的樹。如果能創建一個大致平衡的二叉樹，并讓兄弟子樹的包圍盒不重疊太多，那么將會很便捷。實現這個的一個啟發式方法是在劃分表面到兩個子列表前，先沿著一條軸排序。如果我們使用整數來定義這些軸\(x=0\)、\(y=1\)、\(z=2\)那么有

在排序的時候小心地選擇軸就能提高樹的質量。有個方法是通過讓兩個子樹的包圍盒的總體積最小化來選擇軸。與依次循環使用坐標軸相比，這種方法對于有著分布均勻的小物體的場景來說，不會帶來太大差別，但是對于那些雜亂的場景來說，它帶來的提升可能很大。通過只進行劃分而不是完整的排序，上述的代碼也可以變得更加地有效率。
??另一個可能更好的建立樹的方法是讓子樹包含差不多大小的空間，而不是包含相同數量的物體。為了做到這件事，我們基于空間來劃分表，因此有如下的代碼

雖然這會導致一個不平衡的樹，但是它允許更加輕松地遍歷空白空間，此外還更容易被建立，因為劃分比排序的開銷要低。

均勻空間劃分（Uniform Spatial Subdivision）

??另一個能減少交匯檢測策略是劃分空間，這和層次包圍體有很大的不同。在層次包圍體中，每個物體屬于兄弟節點的其中一個。而在空間劃分中，每個在空間中的點只屬于一個節點。在均勻空間劃分中，場景被劃分到了軸對齊的盒中。這些盒都有相同的大小，盡管它們不一定要是立方體。下圖展示了光線遍歷這些盒的例子

當一個物體被擊中時，遍歷會終止。網格本身應該是表面類的子類，而且應該被實現為指向表面的指針的三維數組。對于空的格子來說，這些指針就是NULL。對于有一個物體的格子，指針會指向那個物體。對于有著更多物體的格子，指針可以指向一個列表或其它網格，又或者是其它的數據結構，比如層次包圍體。
??遍歷是以增量方式完成的，為了了解是怎么具體完成的，我們可以先考慮二維的情況，假設光線方向的分量都為正且光線從網格外出發，網格有\(n_x \times n_y\)個格子且被點\((x_\mathrm{min},y_\mathrm{min})\)和點\((x_\mathrm{max},y_\mathrm{max})\)包圍。
??我們的第一個任務就是找到第一個被光線\(\mathbf{e}+t\mathbfw0obha2h00\)擊中的格子的索引\((i,j)\)，接著需要以正確的順序遍歷格子。因此算法的關鍵是找到開始的格子\((i,j)\)然后決定是要增加\(i\)還是\(j\)。這里要注意，當檢查光線與格子包含的物體的是否相交時，參數\(t\)會被限制在格子內，就如下圖展示的那樣。

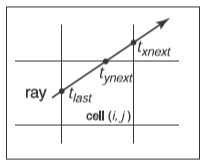
絕大多數的實現都會讓“指向表面的指針”作為三維數組的類型，為了改善遍歷的局部性，三維數組可以被展平成一維數組，這個將在后續討論。

軸對齊的二叉空間劃分（Axis-Aligned Binary Space Partitioning）

??我們也可以使用層次數據結構來劃分空間，例如二叉空間劃分樹（Binary Space Partitioning Tree，BSP tree）。這和后續的用于可見度排序的BSP樹相似，對于光線相交的情況，一般會使用與軸對齊的平面來劃分，而不是與多邊形對齊的平面。
??在這個結構中的節點包含一個切割平面以及一個左子樹和右子樹，每個子樹包含在切割平面一邊的所有物體，穿過平面的物體會被存儲在兩個子樹中。如果我們假設切割平面平行于\(yz\)平面于\(x=D\)，那么節點類應該是

后續可以推廣到\(y\)和\(z\)切割平面的情況。相交的代碼可以使用遞歸的方式來實現，而且應該考慮如下圖所示的四種情況

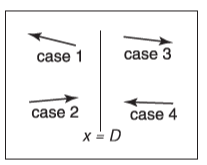
我們讓光線從參數\(t_0\)開始傳播，于是有

\[\mathbf{p} = \mathbf{a} + t_0 \mathbf{b} \]

下面為四種要考慮的情況

光線只與左子樹交互，我們不需要檢測其與切割平面的相交。這只在\(x_p<D\)且\(x_b<0\)時發生。
測試與左子樹的物體相交后發現沒有擊中，接著測試與右子樹物體的相交。我們需要找到在\(x=D\)時的光線參數，把求交范圍限制在子樹內部。這種情況只在\(x_p<D\)且\(x_b>0\)時發生。
這種情況和第一種情況類似，只會在\(x_p>D\)且\(x_b>0\)時發生。
這種情況和第二種情況類似，只會在\(x_p>D\)且\(x_b<0\)時發生。

因此，處理這些情況的代碼為

上述的代碼非常簡潔，然而為了開始，我們需要擊中根節點對象的包圍盒，來初始化遍歷。此外我們需要解決的一個問題是切割平面可能會沿著任意軸，對此我們可以在bsp-node類中增加一個整數成員來指定軸，如果點允許索引操作，那么上方的代碼只需要一些小的修改，例如把

\[x_p = x_a + t_0 x_b \]

修改成

\[u_p=a[\mathrm{axis}]+t_0b[\mathrm{axis}] \]

這會導致一些額外的數組索引，但是不會產生更多的分支。
??雖然一個bsp-node的處理比一個bvh-node的處理要快，但是一個表面可能會出現在多個子樹中，這意味著會有更多的節點，帶來了潛在的更高的內存使用。和構建BVH樹相似，我們可以選擇一個軸在一次循環中進行分割，每次可以分成一半或者采用其它更精細的方式。

用于可見度的BSP樹（BSP Tree for Visibility）

??空間數據結構可以解決的另一個問題是，當視點變化時確定場景中的物體的可見度順序。如果我們要為一個由平面多邊形組成的場景生成圖像，那么可以使用一種二叉空間劃分結構，這和上個部分的軸對齊的二叉空間劃分結構有點類似，區別是對于可見度排序來說，不會使用軸對齊的切割平面，而是與幾何體共面的平面。這樣就有了一個優雅的BSP樹算法，用于從前往后排序表面。對于BSP樹的一個關鍵是使用預處理創建一個對任意視點都有用的數據結構。因此，在視點變化時，可以使用相同的數據結構而不需要進行修改。

BSP樹算法的概述（Overview of BSP Tree Algorithm）

??BSP樹算法是畫家算法（Painter's Algorithm）的一個例子，畫家算法會從后往前繪制每個物體，就如下圖所展示的那樣

它可以像下面這樣被簡單地實現

在第一步也就是排序，我們遇到的第一個問題是物體之間并不總是有明確的順序關系，比如下圖所展示的循環遮蔽的情況。

??BSP樹算法只有在構成場景的任意多邊形不穿過場景中的其它多邊形定義的平面時才有用，不過這個限制可以被另一個預處理步驟放寬。對于接下來的討論，我們只考慮三角形這一情況。
??BSP樹的基本想法可以使用兩個三角形\(T_1\)和\(T_2\)來說明，首先得回顧隱式平面方程\(f(\mathbf{p})\)，對于位于平面不同側的點來說，函數值有不同的符號，于是我們可以利用\(T_1\)三角形定義的平面的隱式方程\(f_1(\mathbf{p})\)。假設\(T_2\)三角形的所有頂點在\(f_1(\mathbf{p})<0\)這一側，那么對于任意視點\(\mathbf{e}\)有如下的繪制算法。

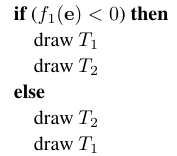
這么做的原因很簡單，當視點\(\mathbf{e}\)和\(T_2\)三角形同側時，不管視點\(\mathbf{e}\)在哪，在渲染出來的圖像中，\(T_1\)三角形永遠都不會部分覆蓋\(T_2\)三角形。反之，則\(T_2\)三角形永遠都不會部分覆蓋\(T_1\)三角形，下方是一張形象的示例圖

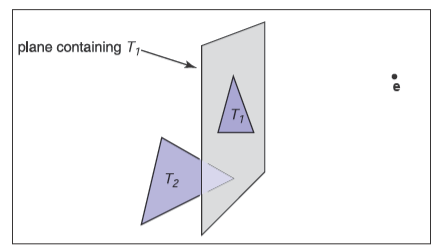
由此，我們能構建一個以\(T_1\)為根的二叉樹數據結構，樹的負分支包含那些頂點\(f_i(\mathbf{p})<0\)的三角形，樹的正分支包含那些頂點\(f_i(p)>0\)的三角形，接著我們就能以如下順序進行繪制

對于任意的視點\(\mathbf{e}\)來說，上述代碼都能正確執行。唯一的問題是當三角形穿過了又其它三角形定義的平面時，代碼就不能正確工作。在這種情況下有兩個頂點會在一側，剩下一個頂點會在另一側，因此我們要把這種三角形“切割”成更小的三角形。

樹的構建（Building the Tree）

??如果數據集中沒有三角形穿過其它三角形定義的平面，那么我們能用如下的方法來構造樹。

我們唯一要解決的是下圖所示的三角形穿過劃分平面的情況。

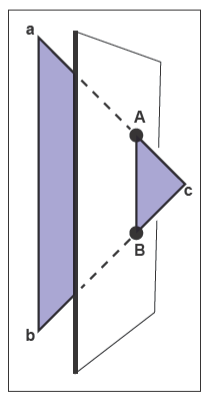
在上圖這種情況中，我們首先得求出交點\(\mathbf{A}\)和\(\mathbf{B}\)，接著就能得到三個小三角形，分別為

\[\begin{align*} T_1 = (\mathbf{a},\mathbf{b},\mathbf{A})\\ T_2 = (\mathbf{b},\mathbf{B},\mathbf{A})\\ T_3 = (\mathbf{A},\mathbf{B},\mathbf{c}) \end{align*} \]

這里要注意一點，小三角形頂點的順序很重要，因為要保持和大三角形相同的朝向。假設\(f(\mathbf{c})<0\)，那么把這三個三角形添加到兩個子樹的代碼為

此外我們還要注意精度問題，比如之前所展示的例子的\(\mathbf{c}\)點有可能離分割平面很近，這就導致了切割出來的其中一個三角形非常小，因此我們要檢測這種情況而且最好不做處理，于是有如下的代碼

切割三角形（Cutting Triangles）

??對于切割三角形來說，有不同的情況要考慮，我們應該利用BSP樹的構建是個預處理過程，最高效率不是關鍵，寫出清晰且緊湊的代碼。一個好的技巧是通過交換頂點，確保\(\mathbf{c}\)頂點總是單獨在另一邊的那個頂點。這么處理后就只需要處理一種情況，于是有如下的代碼

當頂點被交換的時候，我們應該執行兩次交換來確保頂點有逆時針順序。這里要注意，當被切割的三角形的其中一個頂點正好在平面上時，會生成一個有\(0\)面積的三角形，不過我們可以忽略這種情況，因為風險不是很大，光柵化代碼會幫我們處理這種情況。如果實在覺得不行，也可以檢測面積，防止\(0\)面積的三角形被加入樹。
??為了計算\(\mathbf{A}\)和\(\mathbf{B}\)，我們有參數直線

\[\mathbf{p}(t) = \mathbf{a} + t(\mathbf{c-a}) \]

與平面\(\mathbf{n} \cdot \mathbf{p} + D = 0\)求交則有

\[\mathbf{n} \cdot (\mathbf{a} + t(\mathbf{c-a})) + D = 0 \]

解得

\[t = - \frac{\mathbf{n} \cdot \mathbf{a} + D}{\mathbf{n} \cdot (\mathbf{c-a})} \]

令求得的參數為\(t_A\)，那么求得\(\mathbf{A}\)為

\[\mathbf{A} = \mathbf{a} + t_A (\mathbf{c-a}) \]

我們可以使用相同的方法來計算\(\mathbf{B}\)。

樹的優化（Optimizing the Tree）

??樹的構建只是個預處理過程，因此效率不是太重要，而遍歷BSP樹所花費的時間會和樹中的節點數量成比。每個節點對應著一個三角形，節點的數量會取決于三角形被添加到樹中的順序，就比如下圖這個例子

如果讓圖中的大三角形為根節點，那么樹中會有兩個節點。但是如果讓小三角形為根節點，那么會有更多的節點，這是因為大三角形被切割成了更多的小三角形。
??要找到最好的順序非常難，對于\(N\)個三角形來說就有\(N!\)個可能，嘗試每種可能是不實際的。有一個替代方法是，進行隨機排列選出最好的那一個。

分塊多維數組（Tiling Multidimensional Arrays）

??高效地利用內存層次結構對于為現代架構設計算法來說，是至關重要的任務。確保多維數組的數據有好的存儲布局是通過分塊（Tiling）或分磚（Bricking）做到的。一個傳統的二維數組的存儲是通過使用一維數組和索引機制做到的。例如一個\(N_x \times N_y\)的數組會存儲在一個長度為\(N_xN_y\)的一維數組中，二維索引\((x,y)\)會使用下方的公式映射到一維索引。

\[\mathrm{index} = x + N_xy \]

下圖展示了在這種情況下，內存布局的一個示例。

從圖中我們能看出一個問題，二維位置相鄰的元素在實際的一維空間中可能不會相鄰。如果\(N_x\)較大，那么會有較差的內存局部性。標準的解決方案是用分塊（Tile）讓行和列的內存局部性更加均勻。一個使用\(2 \times 2\)分塊的例子如下所示

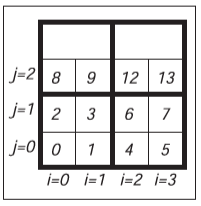
在后續的部分，我們將會討論使用這種數組的索引的細節。在那之后還有更復雜的例子，即在三維數組上使用兩級分塊。
??一個關鍵的問題是分塊要有多大。在實踐中，分塊的大小應該與機器的內存單元大小接近。例如，如果我們在一臺有著128字節大小的緩存行的機器上使用16位數據，那么8x8的分塊正好能裝進一個緩存行。如果使用的是32位的浮點數，一個緩存行能容納32個元素，5x5的分塊顯得稍微小了點，而6x6的分塊又稍微顯得大了點。由于還有更大粒度的內存單位，比如內存頁，因此可以采用有著類似邏輯的分層分塊方法。

對于二維數組的一級分塊（One-Level Tiling for 2D Arrays）

??假設我們使用\(n \times n\)的分塊來分解\(N_x \times N_y\)的數組，下圖為一張示例圖

需要的分塊的數量為

\[\begin{align*} B_x &= N_x / n \\ B_y &= N_y /n \end{align*} \]

在這里我們假設\(N_x\)和\(N_y\)能被\(n\)整除，否則數組需要被填充（Padding）。比如，如果\(N_x=15\)且\(n=4\)，那么\(N_x\)應該被修改為16。為了得出這種數組的索引方法，我們首先得計算分塊的索引\((b_x,b_y)\)

\[b_x = x \div n \]

\[b_y = y \div n \]

這里的\(\div\)表示的是整數除法，比如\(12 \div 5 = 2\)。求得分塊的索引后，那么某個分塊中的第一個元素的索引為

\[\mathrm{index} = n^2 (B_x b_y + b_x) \]

接著我們需要求元素在分塊內部的索引\((x^\prime,y^\prime)\)，實際上就是取模運算，即

\[x^\prime = x \; \mathrm{mod} \; n \]

\[y^\prime = y \; \mathrm{mod} \; n \]

求出分塊內部的索引后，那么元素相對于分塊內第一個元素的索引的偏移\(\mathrm{offset}\)為

\[\mathrm{offset} = y^\prime n + x^\prime \]

因此把元素的二維索引映射到一維索引的公式為

\[\begin{align*} \mathrm{index} &= n^2 (B_x b_y + b_x) + y^\prime n + x^\prime \\ &=n^2((N_x \div n)(y \div n)+x \div n) +(y \; \mathrm{mod} \; n)n+(x \; \mathrm{mod} \; n) \end{align*} \]

這個表達式包含很多乘法、除法、取模，在某些處理器上的開銷很昂貴。當\(n\)是\(2\)的冪時，這些操作可以被轉化為移位和位邏輯操作。然而正如之前提到的那樣，\(n\)的大小不總會是\(2\)的冪。有些乘法運算可以被轉化為移位或加法操作，但是除法和取模則更棘手。索引雖然可以通過增量的方法來計算，但是這需要維護計數器，從而帶來大量的比較操作，而且會導致分支預測性能不佳。
??實際上有一種簡單的解決方法，索引表達式可以被寫為

\[\mathrm{index} = F_x(x) + F_y(y) \]

而

\[\begin{align*} F_x(x)&=n^2(x \div n)+(x \; \mathrm{mod} \; n) \\ F_y(y)&=n^2(N_x \div n)(y \div n) + (y \; \mathrm{mod} \; n)n \end{align*} \]

我們可以預計算\(F_x(x)\)和\(F_y(y)\)的值并制成表，接著在使用的時候讓\(x\)和\(y\)作為索引來找到對應的值。即使是數據規模非常大的情況下，表的總大小也可以被放進處理器的一級數據緩存。

三維數組的二級分塊的例子（Example: Two-Level Tiling for 3D Arrays）

??有效利用\(\mathbf{TLB}\)（Translation Lookaside Buffer，快表）也是算法性能中的一個至關重要的因素。可以使用類似的方法來提高三維數組的\(\mathbf{TLB}\)命中率：先將數組劃分為\(n \times n \times n\)的小單元，再將這些小單元組合成\(m \times m \times m\)的大塊。比如一個\(40 \times 20 \times 19\)的三維數據體可以被劃分為\(4 \times 2 \times 2\)的宏塊，每個宏塊由\(2 \times 2 \times 2\)的小塊組成，每個小塊又包含\(5 \times 5 \times 5\)的單元。在這里對應的參數為\(m=2\)，\(n=5\)。由于\(19\)不能被\(mn=10\)整除，因此需要對數組進行一級填充。從經驗來看，對于16位數據集，較為合適的宏塊大小為\(m=5\)。而對于浮點數據集，較合適的宏塊大小為\(m=6\)。
??對于任意\((x,y,z)\)，索引計算的表達式為

\[\begin{align*} \mathrm{index} = &((x \div n)\div m)n^3m^3((N_z \div n)\div m)((N_y \div n) \div m) \\ &+((y \div n) \div m)n^3m^3((N_z \div n) \div m) \\ &+((z \div n) \div m)n^3m^3 \\ &+((x \div n) \; \mathrm{mod} \; m) n^3 m^2 \\ &+((y \div n) \; \mathrm{mod} \; m)n^3 m \\ &+((z \div n) \; \mathrm{mod} \; m)n^3 \\ &+(x \; \mathrm{mod} \; n)n^2 \\ &+(y \; \mathrm{mod} \; n)n \\ &+(z \; \mathrm{mod} \; n) \end{align*} \]

其中\(N_x\)、\(N_y\)、\(N_z\)分別為數據集的大小。
??與之前的二維數組的一級分塊類似，表達式可以被寫為

\[\mathrm{index} = F_x(x)+F_y(y)+F_z(z) \]

而

\[\begin{align*} F_x(x) = &((x \div n)\div m)n^3m^3((N_z \div n)\div m)((N_y \div n) \div m)\\ &+((x \div n) \; \mathrm{mod} \; m) n^3 m^2 \\ &+(x \; \mathrm{mod} \; n)n^2 \\ F_y(y) = &((y \div n) \div m)n^3m^3((N_z \div n) \div m) \\ &+((y \div n) \; \mathrm{mod} \; m)n^3 m \\ &+(y \; \mathrm{mod} \; n)n \\ F_z(z) = &((z \div n) \div m)n^3m^3 \\ &+((z \div n) \; \mathrm{mod} \; m)n^3 \\ &+(z \; \mathrm{mod} \; n) \end{align*} \]

posted @ 2025-09-07 23:39 TiredInkRaven 閱讀(31) 評論(0) 收藏舉報

刷新頁面返回頂部

TiredInkRaven

《Fundamentals of Computer Graphics》第十二章 圖形數據結構

開篇