開篇

??在圖形學中，我們通常會處理連續變量的函數，比如圖像就是這樣的例子。但是隨著越來越深入地學習，會遇到更多這樣的函數。連續函數的本質導致它們不能直接在計算機中被表示，我們只能用有限數量的比特位來表示它們。最好用之一的方法是用函數的采樣（Sample）來表示連續函數，即存儲函數在不同點的值，然后在需要的時候重建（Reconstruct）點之間的值。
??你現在應該已經熟悉了使用二維像素網格來表示圖像這一想法，這實際上就是個采樣表示的例子。想象一張圖像被數字相機拍攝，在相機的鏡面上形成的圖像是在圖像平面上的位置的連續函數，相機會把連續函數轉化為二維樣本的網格。從數學上來說，相機把\(\mathbb{R}^2\)類型的函數轉化到了\(\mathbf{C}\)即顏色樣本的二維數組，或是把\(\mathbb{Z}^2\)類型的函數轉化到了\(\mathbf{C}\)。
??另外一個采樣表示的例子是平板電腦，當使用觸控筆在屏幕上移動時，筆頭的位置是隨時間連續變化的，但是平板只能在某個時間點測量位置，從而記錄到一序列的二維位置。一個動作捕獲（Motion Capture）系統做的也是相同的事，通過演員身上的特殊標記連續進行位置測量。上升一個維度到醫用CT掃描儀，它會非侵入性地掃描人的身體內部，測量密度關于位置變化的函數，掃描儀輸出的結果是三維密度網格。
??這些例子雖然看起來不同，但是可以用相同的數學來解決。不論如何在一個或多個維度上的晶格（Lattice）點采樣函數，在任何情況下都要能通過采樣獲得的樣本重建原始的連續函數。
??對于二維圖像來說可能有像素就足夠了，在相機離散化圖像后就不需要考慮原來的連續函數。但是有時我們可能想讓屏幕上的圖像變大或者變小，特別是用到非整數縮放因子。結果發現最簡單的用于實現的算法表現很差，會引入明顯的視覺偽影也就是走樣（Aliasing）。解釋為什么走樣發生以及理解該怎么避免這種現象需要采樣理論背后的數學。最終得到的算法很簡單，不過在它們背后的原理很重要，以及讓它們表現良好的細節可能很微妙。
??當然了在計算機中表示連續函數并不是圖形學獨有的，從數字音頻到計算物理學的一些應用場景都有用到采樣表示。圖形學只是其中之一，用到了里面一些相關的算法和數學。這章將從使用一維數字音頻的例子總結采樣和重建開始，接著展示一或二維中為采樣和重建奠基的基礎數學和算法。最后將深入到頻域中的細節，它們為這些算法的行為提供了很多見解。

數字音頻：在一維中采樣（Digital Audio: Sampling in 1D）

??在音頻記錄中，麥克風會把在空氣中以壓力波存在的聲音轉換到隨時間變化的電壓，轉換成的電信號必須被存儲來讓它能在后續的某個時間被回放。回放涉及到把存儲的電信號發送給揚聲器，接著揚聲器把電信號轉化為壓力波。
??記錄音頻信號的數字方法使用采樣：一個模數轉換器每秒測量幾千次電壓，生成的整數流能在任意媒介上存儲。在回放的時候數據以恰當的速率被讀取，被送到一個數模轉換器。數模轉換器根據輸入的數字產生對應的電壓，最終產生的電信號和聲音輸入時記錄的電信號一致。下圖大致展示了聲音采樣和重建的過程

??事實證明，好的回放效果所需要的每秒采樣數取決于我們要記錄的聲音的聲調。可以良好地還原低音提琴和踢鼓的聲音的采樣率在回放短笛和鐃鈸時會產生怪異的聲音，當使用更高的采樣率時這種問題會消失。為了避免這些欠采樣（Undersampling）偽影，數字音頻記錄器會對輸入模數轉換器的信號進行濾波，移除那些會導致問題的高頻率信號。
??另一種問題發生在輸出這邊，數模轉換器產生的電壓會在新樣本輸入時改變，直到下一個樣本前都會保持不變，這樣就產生了一種階梯形的坐標圖，這些階梯的效果就好像噪音，會增加一種高頻且依賴于信號的嗡嗡聲。為了移除這種重建偽影，數字音頻播放器會對數模轉換器的輸出進行濾波從而讓波形變平滑。

采樣偽影和走樣（Sampling Artifacts and Aliasing）

??相同類型的欠采樣和重建偽影也會發生在圖形學中的圖像或其它被采樣的信號中，而且解決方案是一樣的即在采樣前濾波和在重建后再次濾波。使用過低采樣頻率會產生問題的一個例子如下

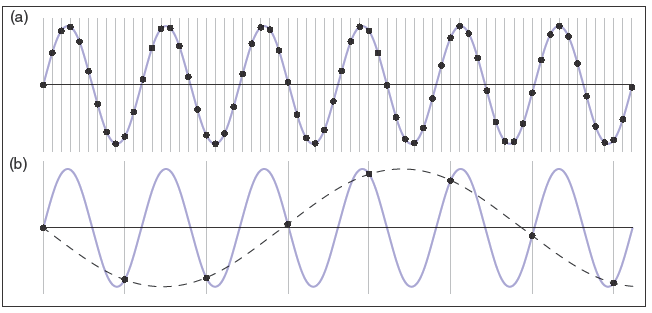
上圖展示了使用兩個不同的采樣頻率采樣正弦波，上面的為10.8樣本每周期，下面的為1.2樣本每周期。使用更高采樣率得到的樣本明顯能更好地捕捉信號，使用更低采樣率導致了無法很好地重建原信號，反而看起來更像一個低頻率的正弦波。
??一旦采樣完成了就不知道快和慢的正弦波中哪個是原始信號，因此沒有哪一種方法能恰當地在兩種情況下重建信號，因為高頻信號在“假裝”是低頻信號，這一現象被稱為走樣（Aliasing）。
??當采樣和重建有缺陷導致在令人驚訝的頻率上出現偽影時，走樣就會出現。在音頻中，走樣以額外的怪異音調出現。當一個鈴以10KHz響動時，如果以8KHz的頻率采樣則會產生6KHz的奇怪音調。在圖像中，走樣以摩爾紋（Moiré patterns）的形式出現，這是采樣網格和圖像中的常規特征交互的結果。下圖是個相關的例子

??另一個在合成圖像中走樣的例子是熟悉的階梯式直線，由上圖的b圖可見。這是一種小尺度特征，會在不同的尺度上產生偽影，對于淺斜率直線來說會產生非常長的階梯。
??采樣和重建的基本的問題可以被簡單地理解為特征太小了或太大了，但是這樣的話有些更加量化的問題就更難回答，比如

1. 多高的采樣率能保證好的效果？
2. 對于采樣和重建來說要使用哪種合適的濾波方法呢？
3. 避免走樣需要多少平滑度？

卷積（Convolution）

??在我們討論采樣和重建的算法前，我們將首先了解它們基于的叫做卷積（Convolution）的數學概念。卷積是個簡單的數學概念，它是用于采樣、濾波、重建的算法的基礎，此外它還是我們在這章中分析這些算法的基礎。
??卷積是作用于函數上的運算，它會取兩個函數進行結合，然后得出一個新函數。在這里卷積算子為星號，對函數\(f\)和\(g\)施加卷積的結果為\(f \star g\)，我們稱\(f\)與\(g\)卷積，\(f \star g\)為卷積的結果。
??卷積可以作用于連續函數或離散序列，而且不止能用于一維。我們首先從離散的一維情況開始，接著再到連續函數和二維還有三維的函數。為了定義方便，通常假設函數的定義域是無窮的。當然了在實際情況下通常會在一個地方停下，因此我們得用特殊的方法來處理端點情況。

移動的平均（Moving Average）

??為了了解卷積的基本情況，考慮使用移動的平均來平滑一個一維函數，如下圖所示

為了在任一點得到一個平滑的值，那么就得計算任意方向\(r\)距離內的函數平均值，距離\(r\)就是平滑操作的半徑，它決定到底有多平滑。我們可以使用數學的方法來實現這個想法，如果要平滑一個連續函數\(g(x)\)，平均意味著先求一個區間上的積分，接著再除以區間的長度

在另一方面如果我們平滑一個離散函數\(a[i]\)，平均意味著先求一定范圍索引內的和，接著再除以數值的數量

這種移動的平均想法是卷積的精髓，不過再卷積中移動的平均是加權的。

離散卷積（Discrete Convolution）

??我們將從卷積的最具體的例子開始，卷積一個離散序列\(a[i]\)與另一個離散序列\(b[i]\)，卷積的結果為另一個離散序列\((a \star b)[i]\)。過程就像使用移動的平均那樣來平滑\(a\)，但是這一次會使用\(b\)序列來給每個樣本一個權重，而不是使用相同的權重。一個示例圖如下所示

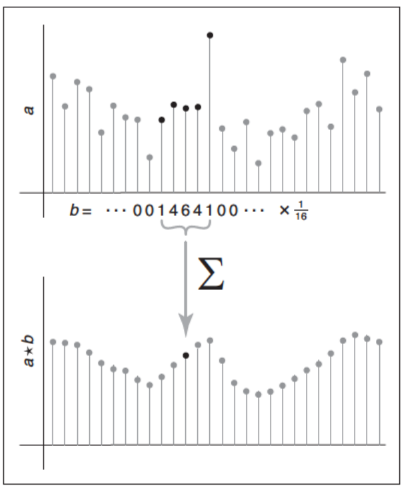
省略掉邊界情況可以得到\((a \star b)\)為

??看到這里你可能會想這個公式為什么用的是\(b[i-j]\)而不是\(b[-i+j]\)。在信號處理中，卷積可以表示成一個系統對輸入信號的響應，這個時候\(b[k]\)表示的是一個輸入在發生\(k\)個單位時間后，這個輸入對當前輸出的影響因子，因此應該使用前者。只不過對于計算機圖形學來說，用到的大部分權重序列都是對稱的，使用后者在很多時候也能得到正確的結果。
??在計算機圖形學中，兩個中的一個函數通常有有限的支持，這意味著只有在一個有限的區間內才是非\(0\)的。如果\(b\)有有限的支持且半徑為\(r\)，那么當\(|k|>r\)時\(b[k]\)都會等于0。在這種情況下求和表達式可以寫為

用偽代碼表達則為

卷積濾波器（Convolution Filters）

??卷積非常重要，因為我們能使用它來實現濾波。回顧剛開始的那個移動的平均的例子，實際上可以把平滑操作理解為使用特定的序列進行卷積。當我們計算有限范圍內的平均值時，實際上使用的是一個在范圍內有相同值其它地方都為\(0\)的權重序列。這種在區間內有常量其它地方為\(0\)的濾波器叫方框濾波器（Box Filter）。對于一個有著半徑\(r\)的方框濾波器來說，權重為\(1/(2r+1)\)，因此

就像這個例子一樣，卷積濾波器通常都被設計來讓它們的總和為\(1\)，這樣就不會影響信號的總體水平。對于濾波的簡單例子來說，信號可以是階躍函數（Step Function）

濾波器可以是中心在\(0\)的五點方框濾波器

對于\((a \star b)[i]\)的計算來說，可以理解為先將\(b\)繞中心進行反轉，接著再往右平移\(i\)個單位，然后求\(a\)序列與反轉并平移后的\(b\)序列的每個元素之間的乘積的總和，直到超出濾波半徑\(r\)。下面是一個形象的示例圖

卷積的屬性（Properties of Convolution）

??看到這里，你會感覺卷積似乎是個不對稱操作，\(a\)序列是要被平滑的，而\(b\)序列會提供權重。實際上反過來也是有效的，也就是說濾波器和信號之間是可互換的。證明這一點很簡單，之前說過在相乘求總和前要進行的操作是：對濾波器\(b\)進行反轉然后再平移，這個時候你就會發現這兩個操作實際上是相對的，我們完全可以把\(a\)繞中心進行反轉，接著再往右平移\(i\)個單位，然后求反轉并平移后的\(a\)序列與\(b\)序列的每個元素之間的乘積的總和。因此可以得到卷積表達式還可以為

這和\((1)\)式簡直長得一模一樣。因此對任意\(a\)序列和\(b\)序列可以得到\((a \star b)=(b \star a)\)，我們稱卷積為交互運算。更一般地說，卷積類似乘法操作，有著交換律和結合律，此外對加法來說還有分配律。因此有下面的關系

??此外在離散卷積中有一種簡單且特殊的濾波器\(d\)，它會使\((a \star d)[i] = a[i]\)。這里你可能很快就想到了，離散序列\(d\)應該長這樣

事實上它通常被稱為克羅內克\(\delta\)或單位沖激序列。

用移位的濾波器進行卷積（Convolution as a Sum of Shifted Filters）

??\((1)\)式描述的卷積操作可以被理解為把濾波器反轉并移動到\(i\)索引處，計算\(i\)索引處周圍的信號對\((a \star b)[i]\)的影響。除了這樣還可以被理解為對于每個\(j\)索引處的信號，把濾波器反轉并移動到\(j\)索引處，計算這個信號對周邊\(i\)索引處\((a \star b)[i]\)的影響。下方有個形象的示例圖

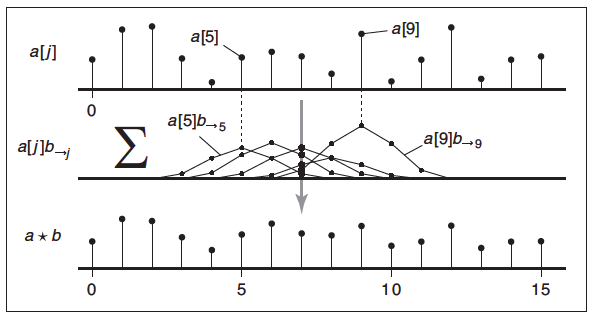
??把濾波器反轉并移動到\(j\)索引處，求得\(j\)索引處的信號\(a[j]\)對\(i\)索引處\((a \star b)[i]\)的影響因子為\(b[i-j]\)，上述操作可以被寫為\(b_{\rightarrow j}[i]\)，這樣可以得到\((1)\)式的另外一種表達形式為

卷積連續函數（Convolution with Continuous Functions）

??在計算機程序中要處理的大多都是離散序列，采樣后的序列都是被用來表達連續函數的，不過我們應該也要了解下連續函數的卷積。對于連續函數的卷積我們很容易能得出公式，只需要把\((1)\)式的求和形式替換成積分形式，即

看到這個公式可以想象一個被反轉的濾波器\(g\)正在跟隨\(x\)滑動，在某一刻計算的\(\int_{-\infty}^{+\infty} f(t) g(x-t) dt\)就是\((f \star g)(x)\)。和離散卷積一樣，連續函數的卷積服從交換律和結合律，對加法來說也有分配律。之前提到的對離散卷積的理解也能完全應用于連續函數的卷積，就比如

假如\(f\)為方框函數

由\((4)\)式可得

由于\(f\)這個函數很特殊，用之前講的使用滑動來理解連續函數的卷積的方法，會發現\(f\)與它自己的卷積實際上就是看有多少面積是重疊的。當\(x\)從\(0\)開始線性增加或減少時，重疊的面積會線性減少。因此很容易得到卷積后的新函數

這個函數被稱為帳篷函數（Tent Function），是另外一個常見的濾波器，下方為這個函數的示例圖

狄拉克\(\delta\)函數（The Dirac Delta Function）

??正如之前提到的克羅內克\(\delta\)一樣，連續函數的卷積中也存在類似的東西。它叫狄拉克\(\delta\)函數，這個函數描述了一個位于\(x=0\)處的極窄尖峰，對于所有\(x \neq 0\)來說都有\(\delta(x) = 0\)，它在\(x=0\)時的函數值也沒有明確的定義。但是有

正因為這樣所以有

離散與連續的卷積（Discrete-Continuous Convolution）

??有兩種方法能連接離散和連續的世界，第一種是采樣，即在整數參數時記錄連續函數\(f(x)\)的數值，然后省略掉其他部分，這樣我們就通過\(a[i]=f(i)\)把連續函數\(f(x)\)轉換到了離散序列\(a[i]\)。
??從另一個方向來，把離散的函數或序列轉化為連續函數，叫重建。這是使用另外形式的卷積做到的，在這種情況下我們使用一個連續的濾波器\(f(x)\)對一個離散的序列\(a[i]\)進行濾波

重建后的函數\(a \star f\)在\(x\)的值是在\(x\)附近的每個樣本加權后的總和，權重來自濾波器\(f\)。下方是一張相關的示例圖

??要注意的是，對于離散與連續的卷積，我們一般把序列寫在前面，以便讓求和在整數范圍內進行。和離散卷積一樣，如果求和有范圍也就是知道濾波器的半徑\(r\)，這樣我們就只需要計算范圍內的樣本的影響

這里要注意的是，當一個點離\(x\)的距離正好為\(r\)時，它將不會被算在求和內。這和離散的情況相反，因為離散的情況會包含這樣的點。下面給出實現上方公式的偽代碼。

??和之前說的用移位的濾波器進行卷積一樣，離散與連續的卷積的公式也有另一種形式，即

離散與連續的卷積和樣條有著密切的關系，對于均勻樣條來說，它的參數化曲線正是樣條的基函數和控制點序列的卷積。

在一維以上進行卷積（Convolution in More Than One Dimension）

??至此，關于采樣和重建所說的一切都是在一維上的進行的。在圖形學中，采樣和重建的很多重要的應用都是在二維上進行的，就比如二維圖像。幸運的是采樣算法和理論可以從一維推廣到二維和三維，而且到更遠的維度從概念上來說很簡單。
??從離散卷積的定義開始，我們可以使用嵌套求和推廣到二維

如果\(b\)是個有著半徑\(r\)的有限支持的濾波器，那么有

使用偽代碼表達有

繼續進行推廣可以得到在二維中的連續與連續的卷積和離散與連續的卷積

卷積濾波器（Convolution Filters）

??我們現在已經掌握了卷積的機制，那么可以看看那些在計算機圖形學中被常用的濾波器。下面的濾波器都有一個自然半徑，它是默認大小用于間隔為一個單位的那些樣本的采樣和重建。在這個部分，將使用自然大小定義濾波器。比如對于方框濾波器來說，它的自然半徑為\(1/2\)。此外還讓每個濾波器的積分為\(1\)，因為采樣和重建不能改變信號的平均值。
??后面的一些部分提到的應用會要求濾波器有不同的大小，我們可以通過縮放基礎的濾波器得到，對于濾波器\(f(x)\)，如果有縮放因子\(s\)我們可以得到縮放后的濾波器\(f_s(x)\)

一些卷積濾波器（A Gallery of Convolution Filters）

方框濾波器（The Box Filter）

??方框濾波器是個分段常量函數，它的積分為\(1\)。如果作為一個離散的濾波器，它可以被寫作

這里要注意為了對稱性應該包括端點。如果作為一個連續的濾波器，它可以被寫作

在這種情況下應該排除一個端點，這樣能確保方框的半徑為\(0.5\)，可以被用作一個重建濾波器。這是因為方框濾波器是不連續的，因此邊界情況很重要，對于這種特殊的濾波器，我們應該關注它們。方框濾波器的自然半徑\(r=\frac{1}{2}\)。下圖為這個濾波器在離散和連續的情況下的示例圖

帳篷濾波器（The Tent Filter）

??帳篷或線性濾波器是個連續且分段的線性函數

它的自然半徑為\(1\)。對于這個濾波器來說，它是\(C^0\)連續的，即函數值不會跳躍，我們不需要分開定義它的離散濾波器和連續濾波器，因為離散濾波器只是連續濾波器在整數的采樣。下方是這個濾波器的函數示意圖

高斯濾波器（The Gaussian Filter）

??高斯函數，通常也被稱作正態分布，它在理論和實踐上都是重要的濾波器。在這章的后面將會看到它的一些特殊屬性

參數\(\sigma\)叫標準差，對于這個濾波器來說取一系列的\(\sigma\)都很有用。此外這個濾波器沒有自然半徑，而且通常沒有有限支持的半徑，但是由于它是指數衰減的，它的值會飛快地減小到可以被忽視。當有需要的時候，我們可以取半徑\(r\)并讓外面的函數值都為0，這樣可以省去很多影響不大的計算。這意味著濾波器的寬度和自然半徑可以由實際應用場景來決定，在實踐的時候可以讓\(\sigma\)和\(r\)作為濾波器的屬性，當濾波器被聲明的時候就固定下來，剩下的就是調整縮放因子\(s\)。下方是這個濾波器的示例圖

三次B樣條濾波器

??很多濾波器都是用分段多項式定義的，而三次濾波器有四段，通常被用于重建濾波器。一個這樣的濾波器被稱為B樣條濾波器，因為它的起源就是作為樣條曲線的混合函數

在三次分段曲線中B樣條曲線是特殊的，因為它是\(C^2\)連續的，也就是說它的一階導數和二階導數都是連續的。一個更加簡潔的定義它的方法為\(f_B = f_\mathrm{box} \star f_\mathrm{box} \star f_\mathrm{box} \star f_\mathrm{box}\)。下方為這個濾波器的示意圖

三次Catmull-Rom樣條濾波器

??另一個以樣條命名的三次分段濾波器為Calmull-Rom濾波器，它在\(x=-2,-1,1,2\)時為\(0\)。當被用于重建濾波器時，這種特殊性質會讓卷積后的函數依然過樣本點。

下面是這個濾波器的一個示例圖

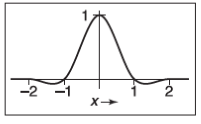
Mitchell–Netravali三次濾波器

??對于所有重要的重采樣圖像應用，Mitchell和Netravali對三次濾波器做了一個研究，并推薦了一個介于前兩個濾波器之間的濾波器作為最佳的綜合性選擇。實際上就是前兩個濾波器的加權的和

下方為這個濾波器的示意圖

濾波器的性質

??濾波器有一些傳統的術語伴隨著它們，我們可以用這些術語來描述濾波器并且在濾波器之間進行比較。濾波器的脈沖響應（Impulse Response）只是函數的另一個名稱，它是濾波器對只包含脈沖的信號的響應。
??當一個連續的濾波器有插值性（Interpolating）時，如果被用于與離散序列卷積的重建，卷積后的函數依然會過原始樣本點，而不是會接近原始樣本點。具有這種性質的濾波器要求\(f(0)=1\)，此外對于任何\(i \neq 0\)的整數都有\(f(i)=0\)。一個示例圖如下方所示

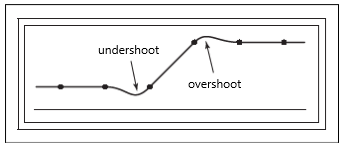
??一個有負值的濾波器會有振鈴效應（Ringing）和過沖（Overshoot），也就是說會在被濾波的函數急劇變化的地方產生額外的振蕩。比如Catmull-Rom濾波器兩邊都有取負值的地方，如果使用它來濾波一個階躍函數，則會略微凸顯階躍，造成低于\(0\)的欠沖和高于\(1\)的過沖，下方有個示例圖

??當一個濾波器被用于重建濾波器并濾波常量序列時，如果濾波后的函數沒有數值上的波動，則稱這個濾波器是無波動（Ripple Free）的。下方是一個相關的示例圖

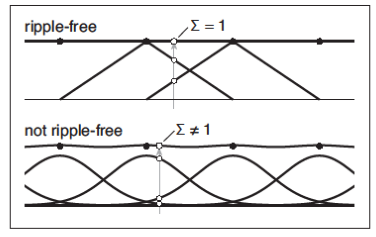
這實際上是要求

除高斯濾波器外，上個部分提供的所有濾波器在他們的自然半徑處都是無波紋的。當它們被用于非整數范圍時，無波紋實際上是非必要的。如果有必要消除離散與連續的卷積的波紋時，處理方法也很簡單，直接把加權求和的值除以權重總和即可

??一個連續的濾波器有一個連續度（Degree of continuity）,實際上就是反復求導看導數是否存在以及是否連續。對于方框濾波器來說，它的函數值是不連續的，因此沒有連續度。對于帳篷濾波器來說，函數值是連續的但是導數不連續，因此它只有\(C^0\)的連續度。一個濾波器如果有連續的導數，就像之前的部分提到的三次分段濾波器一樣，那么就有\(C^1\)的連續度。當然了B樣條實際上有\(C^2\)的連續度。當一個濾波器被用作重建濾波器時它的連續度很重要，因為重建后的函數會繼承濾波器的連續度。

可分離的濾波器（Separable Filters）

??目前我們只討論了些用于一維卷積的濾波器，但是對于圖像以及其它多維的信號來說，我們也需要濾波器。一般來說，任意二維函數都能成為一個二維濾波器，這樣定義他們是有用的。不過在很多情況下，我們能從一維濾波器構造出合適的二維濾波器。最有用的方法就是使用一個可分離的濾波器（Separable Filter），對于一個可分離的濾波器\(f_2\)我們能得到

對于離散的濾波器可以得到

如果\(f_1\)為帳篷函數那么可以得到一個雙線性分段函數\(f_2\)

下方為這個函數的示意圖

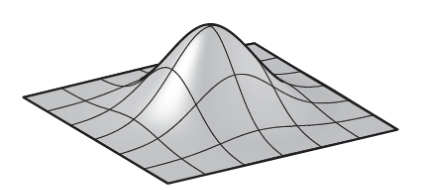
如果我們讓\(f_1\)為高斯函數那么能得到

下方為這個函數的示意圖

??可分離的濾波器有個美妙的地方，這也是它在效率上優于別的二維濾波器的原因。讓我們從離散卷積開始

仔細觀察可以發現最里面的一層求和為

相對于這一層求和來說\(b_1[i-i^\prime]\)是個常量，因此完全可以把它提取到外面一層的求和，于是卷積公式就變成了

如果讓\(i\)為橫坐標，\(j\)為縱坐標，這個時候就發現了\((a \star b_2)[i,j]\)實際上是一縱列的求和乘以一個因子加上另一縱列的求和乘以另一個因子，一直到求和完畢。此外我們還能發現不管是\((a \star b_2)[i+1,j]\)還是\((a \star b_2)[i+2,j]\)，只要\(|k|\)小于等于濾波器的半徑，\((a \star b_2)[i+k,j]\)的計算和\((a \star b_2)[i,j]\)的計算都會用到一些相同的縱列求和的結果，下方是一張形象的用來理解的圖

假如我們要做下面這種類型的大規模計算

for(uint i=0;i<width;i++)
    for(uint j=0;j<height;j++)
        image[i,j] = Convolution(a,b,i,j)

這個時候你可能立馬就想到了，我們可以復用縱列求和的結果，即先進行一次豎直方向上的卷積，計算出中間值也就是所有的位置縱列求和的結果，有了中間值后只要再進行一次水平方向上的卷積，即可完成整個卷積過程。這樣計算就使時間復雜度從\(O(r^2)\)降到了\(O(r)\)，堪稱完美！下面給出實現這個想法的偽代碼

圖像信號處理（Signal Processing for Image）

??目前我們已經以抽象的方式討論過采樣、濾波、重建，而且使用的大多數都是一維信號的例子。在計算機圖形學中許多信號處理的重要應用都是應用于采樣后的圖像的，接下來讓我們看看究竟是如何應用的。

使用離散濾波器濾波圖像（Image Filtering Using Discrete Filters）

??也許卷積的最簡單的應用就是使用離散卷積處理圖像，那些在程序中被廣泛使用的圖像處理功能使用的都是簡單的卷積濾波器，模糊圖像可以通過使用許多常見的低通濾波器做到，從方框濾波器到高斯濾波器。一個高斯濾波器可以產生非常平滑的模糊，因此它被常用于模糊。下方是使用不同濾波器進行模糊的示例圖

??與模糊相反的就是銳化，有一種能做到這樣的方法是使用“反銳化蒙版”過程，就是減去模糊后圖像的一部分，減去一部分后還要防止整體的亮度變化，用公式描述為

其中\(f_{g,\sigma}\)指代的是一個有著寬度\(\sigma\)的高斯濾波器，通過修改\(\sigma\)和\(\alpha\)我們就能獲得不同程度的銳化效果，下方是一個示例圖

??另一個結合兩種離散濾波器的例子是投射陰影，可以通過模糊偏移后的物體輪廓做到，首先可以通過與離心的脈沖卷積完成偏移操作

偏移后接著再模糊，可以得到公式為

下方是一張投射陰影的示例圖

圖像采樣中的抗走樣（Antialiasing in Image Sampling）

??在圖像合成中，我們通常可以用公式計算出圖像在任意一點的顏色，不過我們一般需要圖像的采樣表示，比如光線追蹤就是個例子。以信號處理的語言來說，就是我們有一個連續的二維信號（圖像），需要在一個規則的二維晶格上進行采樣。如果不做任何特殊處理就采樣圖像，結果會出現各種各樣的走樣偽影。下面是一張示例圖

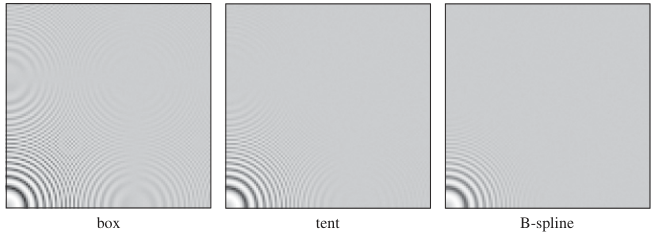
??上圖展示了位于銳利邊緣處的臺階偽影也就是“鋸齒”，此外在一些有重復圖案的地方我們還能發現一些被稱為摩爾紋的寬條紋。這里的問題其實是圖像包含了很多小尺度細節，我們需要在采樣前進行濾波，來讓結果更平滑。一個簡單的濾波器例如方框濾波器可以改善在銳利邊緣處的表現，但是還是會產生一些摩爾紋。對于非常平滑的高斯濾波器來說，它在抗摩爾紋方面則有效得多，但是會造成一些模糊。這兩個例子展示了，在銳度和走樣之間進行衡量是選擇抗走樣濾波器的基礎。下方的圖像展示了使用不同濾波器進行采樣的效果

重建和重采樣（Reconstruction and Resampling）

??最常見之一的圖像操作是重采樣（Resampling），即改變采樣率或改變圖像大小。假設用一個有著3000x2000分辨率的數字相機拍了張圖像，但是我們要在一個1280x1024的監視器上顯示圖像。為了讓圖像在保持\(3:2\)的比例下被顯示，我們需要重采樣到1278x852的分辨率。但是該怎么做呢？一個能做到這個的方法為拋棄像素，在圖像中我們可以距離一定間隔地拋棄像素。這么做雖然速度很快，但是會導致處理后的圖像的質量很差。
??調整圖像大小的方法可以被看作是重采樣操作，我們想要在一個新的維度獲取表示相同圖像的一系列樣本，可以通過采樣從原始樣本重建后的連續函數做到。這樣來看，實際上就是一系列的標準圖像處理操作，首先我們從表示圖像的原始樣本重建一個連續函數，接著對這個連續函數進行采樣。為了避免走樣偽影，每個階段應該用合適的濾波器。
??為了知道算法的細節，最好降到一維來討論。下方為極簡的重采樣一維序列的代碼

參數\(x_0\)為第一個樣本的位置，通過\(x_0+i\Delta x\)我們就能知道后續樣本的位置。像這樣重建后直接進行點采樣還不太對，因為重建后的連續函數可能有非常多的小尺度細節，因此還需要使用一個合適的采樣濾波器\(g\)，讓它與重建后的連續函數卷積，從而得到一個平滑化的連續函數\(g \star (f \star a)\)，最后再進行點采樣就行。此外由卷積的性質可以得到\((g \star f) \star a=g \star (f \star a)\) ,因此重采樣操作變成了點采樣\((g \star f) \star a\)。下方是一張形象的重采樣示例圖

最后一個要解決的問題是如何處理在邊界的情況，你可能也發現了一開始提供的代碼會造成越界讀取。下面有幾個方法

1. 直接停下，等價于使用\(0\)填充超出邊界的那部分。

2. 把讀取位置重定向到邊界位置，如果要讀取\(a[-1]\)那么就返回\(a[0]\)，這等價于使用邊界的值填充超出邊界的那部分。

3. 當接近邊界時修改濾波器，這樣就不會越界讀取。

第一個方法會導致重采樣后的圖像有暗淡的邊緣，第二個方法很容易實現，第三個方法可能是表現最好的。
??選擇用于重采樣的濾波器很重要。有兩個分開的問題，一個是濾波器的形狀，另一個是濾波器的大小（半徑）。因為要選擇的濾波器會同時作為重建濾波器和采樣濾波器，對兩種濾波器的需求影響著如何選擇濾波器。對于重建來說，我們想讓濾波器足夠平滑，避免放大圖像時產生的走樣偽影，此外濾波器還應該是無波紋的。對于采樣來說，濾波器應該足夠大來避免欠采樣以及足夠平滑來避免摩爾紋。下方的圖像展示了這兩種不同的需求

??一般來說，我們會選擇一個濾波器的形狀，然后根據輸入和輸出的相對分辨率來縮放。兩個中更低的分辨率決定了濾波器的大小，當輸出的分辨率比輸入的分辨率小時，對于采樣需要的平滑就高于對于重建需要的平滑，這個時候濾波器的大小就取決于輸出樣本的間距。當重建所需要的光滑占主導地位時，濾波器的大小取決于輸入樣本的間距。
?選擇濾波器得在速度和質量之間進行衡量，常見的選擇是方框濾波器（速度優先）、帳篷濾波器（中等質量）、三次分段濾波器（高質量）。當選擇三次分段濾波器時，平滑度可以通過在\(f_{B}\)和\(f_{C}\)之間進行插值來調整，比如Mitchell-Netravali濾波器就是個好主意。
??在圖像濾波中，可分離的濾波器能提供非常顯著的速度提升，基本想法是先重采樣所有行，產生一個寬度改變但高度不變的圖像，接著再重采樣所有列，這樣就得到了最終結果。下方是一張形象的示例圖

采樣理論（Sampling Theory）

??學復變函數的時候老師根本沒教這里的東西，這部分后面的內容都沒太看懂。可能是我太菜了，應該得很久之后補上了??。