《Fundamentals of Computer Graphics》第八章 視圖
開篇
??上一章主要講了使用變換矩陣和改變坐標系統。有一個次重要的一點就是使用矩陣在物體的三維位置和物體在二維視圖的位置之間進行變換。其中三維到二維的映射叫做視圖變換(Viewing Transformation),這種映射在物體順序渲染中很重要,因為這種渲染方式需要我們快速地為場景中的每個物體找到它在圖像空間的位置。第四章講的光線追蹤,覆蓋了透視視圖和正交視圖,以及如何為給定的視圖生成光線,這章講的就是這個過程的反向過程,即如何使用矩陣變換來表達任意平行或透視視圖。
??要注意的是把點從世界映射到圖像上只能很好地進行線框(Wireframe)渲染,也就是只能看到被繪制的物體的邊緣部分,如下圖所示。而且更近的物體可能不會遮蔽更遠的物體,就像光線追蹤器需要為每個視線找到最近的交點一樣,一個能顯示物體實體表面的基于物體順序的渲染器,需要在影響相同像素著色的所有表面中挑選出最近的表面。在這章,我們假設模型只由三維線段組成,后面的章節將會討論渲染實體表面所需要的機制。
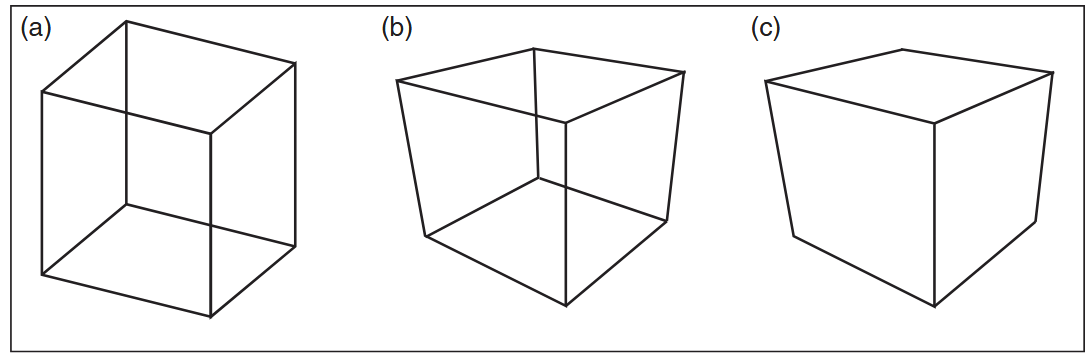
視圖變換(Viewing Transformation)
??視圖變換的作用就是把規范坐標系統的\((x,y,z)\)三維位置映射到以像素為單位的圖像中,不過這稍微有點復雜,因為依賴于相機的位置和朝向還有投影類型、視場、圖像的分辨率。和其它的很多的復雜變換一樣,我們最好把視圖變換拆解為幾個更簡單的變換,許多圖形系統通過一序列的三個變換來達到視圖變換。
-
一個相機變換或者眼變換:它是一個剛體變換,通過把一個有著便捷朝向的相機放到原點來做到,只取決于位置、朝向或者相機的姿態。
-
一個投影變換:它會變換在相機空間中的點并且讓可見的點都落在\(x,y \in [-1,1]\)的歸一化坐標空間內,它只取決于投影的類型。
-
一個視口變換(Viewport Transformation)或窗口變換(Windowing Transformation):它把單位的圖像矩形映射到期望的像素坐標矩形內,它只取決于輸出圖像的大小和位置。
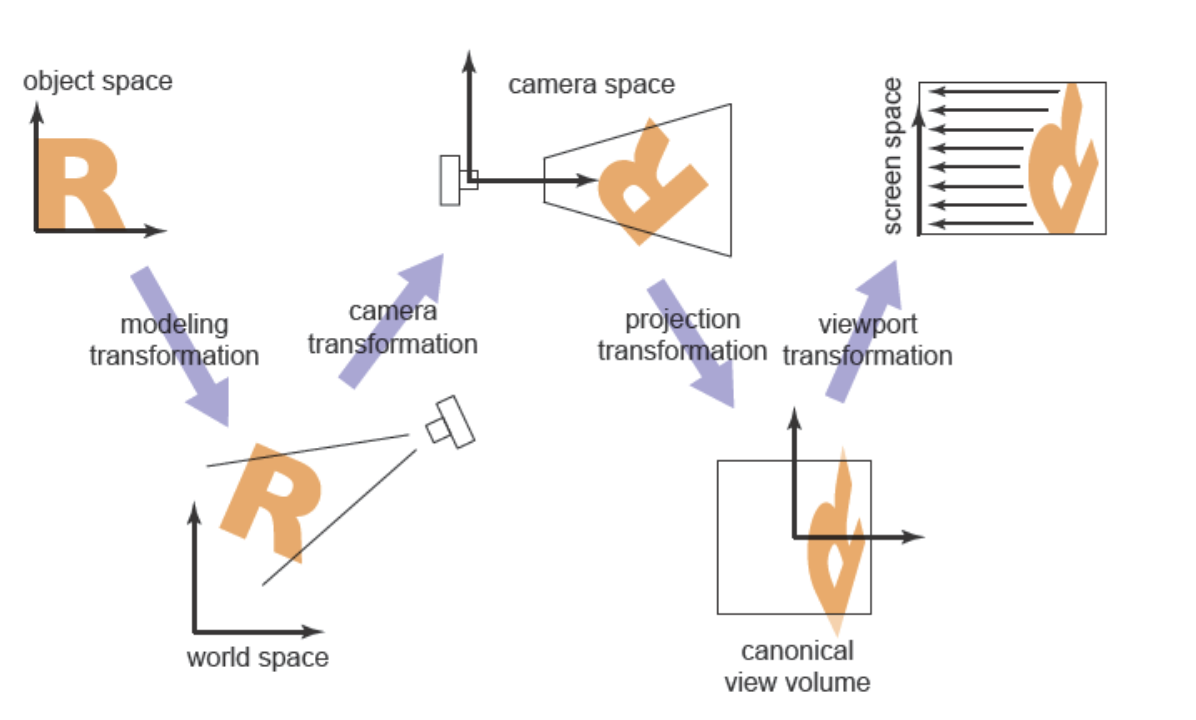
??為了更好的描述如下圖所示的過程的幾個階段,我們給予一些坐標系統名字。
![img]()
相機變換把規范坐標系內的坐標轉換到相機空間(Camera Space)中,投影變換把相機空間中可見的點變換到規范視圖體內,視口變換在最后把規范視圖體映射到屏幕空間(Screen Space)。這幾個單獨的變換都很簡單,下面先從正交投影開始,后續會覆蓋支持透視投影所需要的改變。
視口變換(Viewport Transformation)
??我們假設被看到的物體最后都在規范視圖體(Canonical View Volume)內,而且期望有個正交相機朝著\(+z\)方向觀察。規范視圖體是個立方體,它包含著笛卡爾坐標在\([-1,1]\)之內的所有三維點,也就是\((x,y,z) \in [-1,1]^3\),如下圖所示。我們把\(x=-1\)投影到屏幕左邊,把\(x=1\)投影到屏幕右邊,把\(y=-1\)投影到屏幕底邊,把\(y=1\)投影到屏幕頂邊。如果屏幕左下角的像素的中心坐標為\((0,0)\)且像素中心之間的間距為一單位,那么對于一個每排\(n_x\)像素和每列\(n_y\)像素的屏幕,我們得把正方形\([-1,1]^2\)映射到矩形\([-0.5,n_x-0.5] \times [-0.5,n_y-0.5]\)。
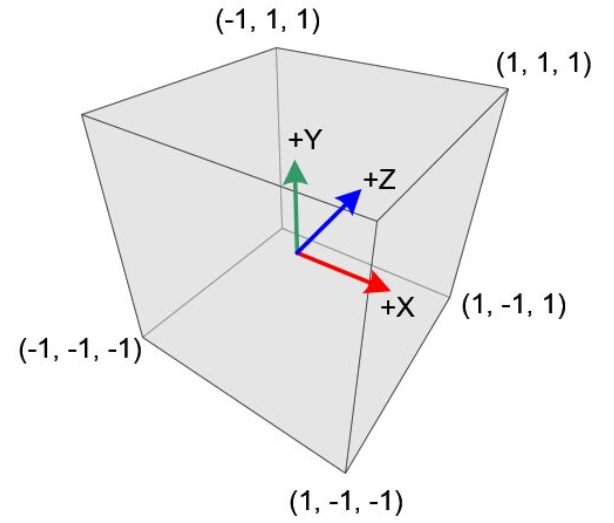
??出于初學的目的,我們先假設所有被繪制的線段在被變換后都完全處于規范視圖體內。不過,當我們之后討論裁剪(Clipping)時會取消這個限制。因為視口變換只是映射矩形,所以視口變換可以如下所示
要注意的是式子中的矩陣忽視了\(z\)坐標,因為點沿著投影方向的距離和它所影響的像素位置無關。在正式稱之為視口矩陣(Viewport Matrix)前,我們增加一行和一列來支持\(z\)坐標,
當前這個章節不需要這些,不過當我們想讓更近的表面遮蔽更遠的表面時會用到\(z\)值。
正交投影變換(The Orthographic Projection Transformation)
??當然了,被看到物體一般都不會直接處于規范視圖體內,我們需要把位于相機空間的視圖體內的物體變換到規范視圖體中。我們首先確定相機空間中的相機的觀察方向為\(-z\)方向并且以\(+y\)為向上方向,對于正交投影來說,相機空間內的視圖體為\([l,r] \times [b,t] \times [f,n]\),我們稱這個視圖體為正交視圖體(Orthographic View Volume),它的包圍平面為:
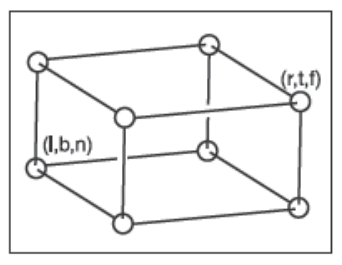
由于我們確定了觀察方向為\(-z\)方向并且以\(+y\)為向上方向,這會導致\(n>f\),可能看起來怪怪的。不過考慮到整個正交視圖體都有負\(z\)值,\(z=n\)的近平面有著更大的\(z\)值因此離觀察者最近,下圖是一個正交視圖體的直觀展示。
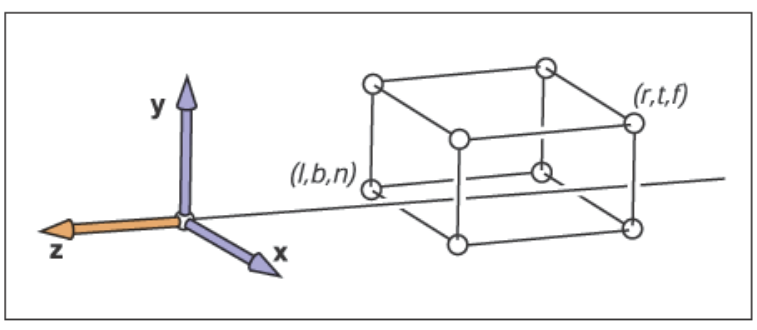
??從正交視圖體到規范視圖體的變換其實是另外一種窗口變換,因此正交投影變換矩陣為
相機變換(The Camera Transformation)
??我們通常可能想在世界空間中的任意位置擺放有著任意朝向的相機,通過相機變換我們就能把位于世界空間中的物體變換到相機空間中,為此我們需要
- \(\mathbf{e}\):眼睛位置
- \(\mathbf{g}\):視線方向
- \(\mathbf{t}\):向上向量(輔助向量)
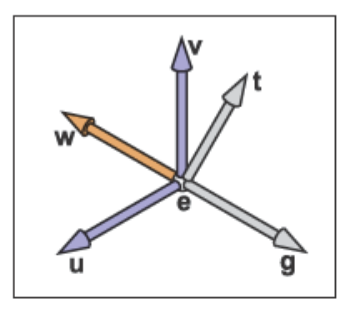
![img]()
要注意的是這里的向上向量\(\mathbf{t}\)只是一個輔助向量,它會把觀察者的頭分成兩半,而且對于站在地面上的人來說會指向天空。有了這些信息,我們就能構建一個坐標系統,以\(\mathbf{e}\)為原點,以\(\mathbf{uvw}\)為基,如上圖所示。利用第二章提到的知識,我們可以這樣得到基向量
得到標準正交基后,接下來我們利用上一章提到的坐標系統之間轉換的知識,把規范坐標系內的物體變換到相機空間中,變換矩陣為
使用這個矩陣變換后,相機會位于相機空間中的原點,并且以\(+y\)為向上方向,向\(-z\)方向觀察,這就對應了上一部分開頭對相機做的假設。這里你可能會問為什么會朝著\(-z\)觀察,這是因為\(\mathbf{w} = - \mathbf{g}/||\mathbf{g}||\),所以觀察方向\(\vec{g}\)在相機空間中為\(-z\)。綜上,用于把規范坐標系內的物體投影到屏幕空間的矩陣\(\mathbf{M}\)為
透視投影變換
??透視投影變換和正交投影變換一樣,都是要把相機空間內的視圖體變換到規范視圖體,不過透視投影變換的視圖體和正交投影變換的六面體不一樣。下圖是這兩者的區別
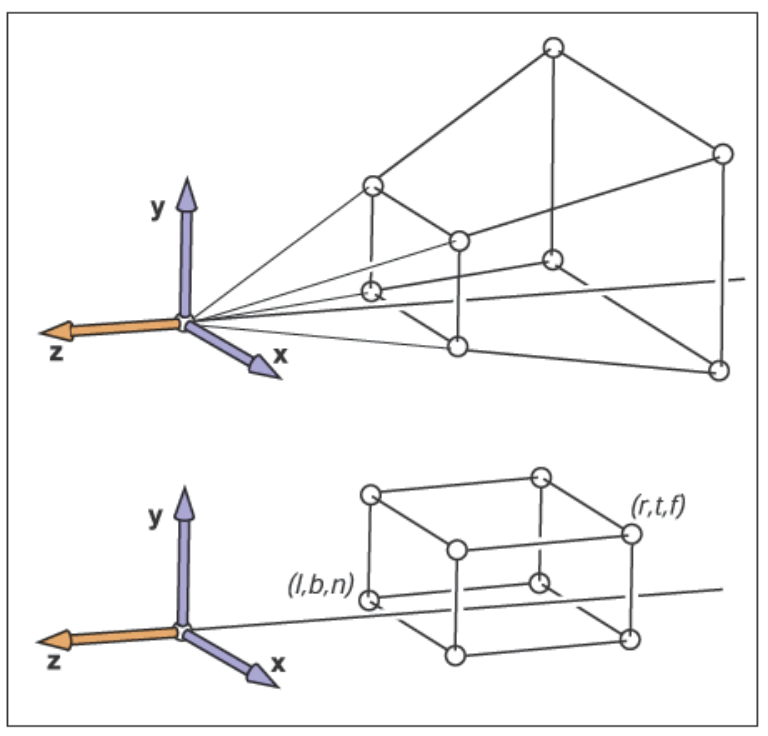
我們稱透視投影變換的視圖體為視錐臺(View Frustum),它是一個視錐體被近平面截去后所獲得的一個棱臺。在這里,我們假設視錐臺是對稱的,接下來要做的就是把這種視錐臺映射映射到規范視圖體\([-1,1]^3\)。
??對于視錐臺內某點的變換,可能很難想出來。但是我們可以這么想,對于視錐臺內任意光線,這上面的點在屏幕空間中都會有相同的\(x\)坐標和\(y\)坐標。于是第一步就是找到光線和相機空間中的圖像平面的交點。
??對于相機空間的視錐臺內的光線,我們可以把它看作是位置關于\(z\)坐標的函數,即
假設相機空間中的圖像平面離相機的距離為\(d\),那么視錐臺內的光線與圖像平面的交點為
我們令交點為\((x_1,y_1,-d)\)。獲得與圖像平面的交點后,接著就能通過一次線性變化把交點的\(x\)、\(y\)坐標變換到屏幕空間中的\(x\)、\(y\)坐標。又因為從屏幕空間變換到規范視圖體只是一次逆線性變換,于是這個時候能得出一個結論:我們只需要一次線性變換就能把交點的\(x\)、\(y\)坐標變換到在規范視圖體內的\(x\)、\(y\)坐標。假設圖像的寬和高分別為\(w\)和\(h\),那么交點的\(x\)、\(y\)坐標的變換公式分別為
那么對于直線上任意一點\((x_2,y_2,z_2)\),我們先把它線性縮放到圖像平面上,縮放因子為\(-d/z_2\),接著再進行線性變換。于是有如下公式
在實踐中,我們通常不會用到圖像平面相關的信息,取而代之的是和近平面或FOV相關的信息。假設近平面的坐標為\(z=n\),且它的左邊和右邊分別有\(x=l\)和\(x=r\),它的底邊和頂邊分別有\(y=b\)和\(y=t\)。利用相似關系我們可以得到
因此,對于視錐臺內任意一點\(\mathbf{p}(x_p,y_p,z_p)\)來說,它的\(x\)坐標和\(y\)坐標的變換公式分別為
到這里就完成了\(x_p\)和\(y_p\)的變換,這個時候你可能會想當然地認為\(z_p\)的變換會利用近平面和遠平面進行線性變換,且公式如下
然而實際情況卻不是這樣,通過翻閱用于不同圖形API的數學庫,你會發現這些數學庫用到的透視投影矩陣都會非線性地映射\(z\)坐標到\([0,1]\)。GLM中的右手透視投影perspectiveRH_NO用到的變換如下
當\(z=n\)時,\(z^\prime=-1\)。當\(z=f\)時,\(z^\prime=1\)。而DirectXMath中的右手透視投影XMMatrixPerspectiveFovRH用到的變換如下
當\(z=n\)時,\(z^\prime=0\)。當\(z=f\)時,\(z^\prime=1\)。這里要說明一下,因為Direct3D用到的規范視圖體的\(z\in [0,1]\),所以配套的DirectXMath數學庫使用的是這種變換。這種非線性映射實際上是為了更好地分配精度,來讓近處的深度精度更高,從而不易觀察出瑕疵。而對于我們的情況來說,可以直接使用GLM中的perspectiveRH_NO函數所用到的變換。因此\(x_p\)、\(y_p\)、\(z_p\)的變換分別為
這個時候會發現這三個分量的變換都得除以\(z_p\),但是我們的\(4\times4\)矩陣不能直接完成這件事。這個時候得利用齊次坐標,我們先賦予\(\mathbf{p}\)齊次坐標到\(\mathbf{p}(x_p,y_p,z_p,1)\)。對于以上三個分量的變換,我們先不考慮\(1/z_p\)對變換的影響,即為每個分量的變換計算除了\(1/z_p\)之外的部分,此外我們還讓變換后的齊次坐標\(w^{new}_p\)等于\(z_p\),這樣就把\(\mathbf{p}(x_p,y_p,z_p,1)\)變換到了四維空間內,這個變換如下所示
我們稱等式右側的矩陣為透視投影變換矩陣,變換后的\(\mathbf{p}^{new}\)的四個分量分別為
最后我們利用\(w^{new}_p\)進行一次透視除法也稱為齊次化(Homogenize),從而得到\(\mathbf{p}^{\prime}=\mathbf{p}^{new}/w^{new}_p\)。
透視變換的一些屬性(Some Properties of the Perspective Transform)
??透視變換的一個重要的屬性就是直線被變換后依舊是直線,平面被變換后依舊是平面。下面我們證明這一點,現有相機空間內的兩點\(\mathbf{q}\)、\(\mathbf{Q}\),我們用參數\(t\in[0,1]\)描述線段\(\mathbf{qQ}\)
令這兩個點在四維空間內的坐標分別為\(\mathbf{r}\)和\(\mathbf{R}\),使用透視矩陣\(\mathbf{M}\)變換可得
齊次化后的三維線段為
經過暴力運算后可重寫成
而\(f(t)\)為
視場(Field-of-View)
??視場即FOV(Field-of-View),它是透視投影變換部分提到的邊緣視線與觀察方向\(\vec{g}\)之間的夾角的兩倍,我們令它為\(\theta\)。之前的部分提到的透視變換矩陣為
\(y\)的縮放因子為
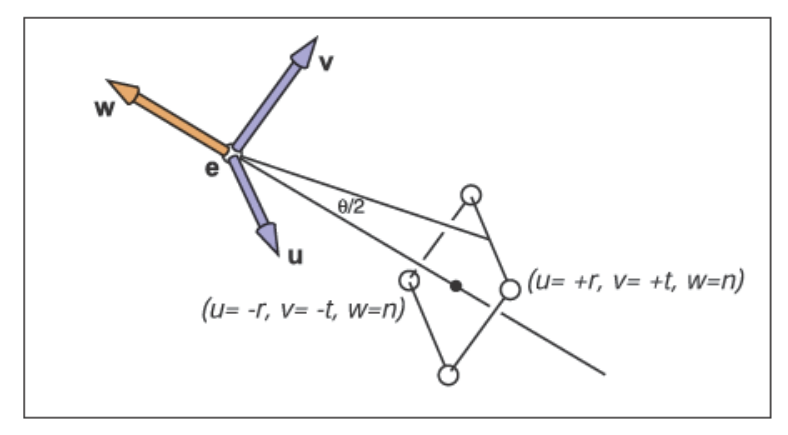
由上圖易得\(\theta\)和它的關系為
因此我們可以通過視場\(\theta\)、近平面和遠平面的\(z\)值的絕對值\(|n|\)和\(|f|\)、輸出圖像的寬高比\(\mathrm{AspectRatio}\)得到透視變換矩陣。下面分別列舉GLM(perspectiveRH_NO)和DirectXMath(XMMatrixPerspectiveFovRH)用到的右手透視變換矩陣\(\mathbf{M}\)。
視圖變換中的邏輯
??這本書有很多地方我覺得都寫得不錯的,不過這一章視圖真的非常非常重要,但是書中只講了“要這么做”,在剛開始寫圖形程序的時候,由于還是一知半解的狀態,因此犯了很多和它相關的錯誤。因此只知道“要這么做”是不夠的!還應該查閱相關資料并且理解“為什么要這么做”,這個部分就來解釋下背后的一些邏輯。
??視口變換還好,沒有什么太要關注的地方。對于相機變換來說你可能會想,為什么相機在相機空間中會向\(z\)軸看以及\(\mathbf{uvw}\)中的\(\mathbf{w}\)基向量為什么和觀察方向\(\vec{g}\)相關聯。這正是因為我們的規范視圖體內的\(z\)坐標是指代遠近的,所以必須這么做。
??此外你還可能想為什么相機變換要使用\(\mathbf{u}\)、\(\mathbf{v}\)、\(\mathbf{w}\)這三個基向量,除了這三個基向量能建立一個右手系外,我們其實還能基于\(\mathbf{u}\)、\(\mathbf{v}\)、\(\mathbf{w}\)使用別的右手系來進行相機變換,例如以\(\mathbf{-u}\)、\(\mathbf{v}\)、\(\mathbf{-w}\)這三個基向量建立右手系。不過使用這三個基向量有個缺點,稍微觀察一下就會發現這么做的話,所有可見的物體在相機空間中都會有\(+z\)值,而且在左手邊的物體在相機空間內都有\(+x\)值,如果直接進行透視除法會發現理論上在左手邊的物體會出現在圖像的右邊!因此我們還得修改透視投影變換矩陣來修正使用\(\mathbf{-u}\)、\(\mathbf{v}\)、\(\mathbf{-w}\)這三個基向量的相機變換矩陣帶來的錯誤。別的右手系就不贅述了,這個時候就發現\(\mathbf{u}\)、\(\mathbf{v}\)、\(\mathbf{w}\)實際上是最便捷的選擇,使用這三個基向量只需除以\(-z\)就能完成透視除法而且不會產生別的錯誤。
本文來自博客園,作者:TiredInkRaven,轉載請注明原文鏈接:http://www.rzrgm.cn/TiredInkRaven/p/18917149



 浙公網安備 33010602011771號
浙公網安備 33010602011771號