開篇
??線性代數的機制可以被用來表達排布三維場景中的物體、使用相機觀察物體、在屏幕上看到物體所需要的許多操作。幾何變換(Geometric Transformation)例如旋轉、平移、縮放、投影都可以通過與矩陣相乘來得到,變換矩陣(Transformation Matrices)就是這章的話題。
??我們可以使用一個\(2 \times 2\)的矩陣來改變或變換一個二維向量
\[\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} a_{11}x+a_{12}y \\ a_{21}x+a_{22}y \end{bmatrix}
\]
這種簡單的取一個二維向量產生另外一個向量的矩陣乘法,就叫做線性變換(Linear Transformation),使用這種簡單的公式可以達到許多不同類型的有用的變換。
縮放(Scaling)
??最基礎的變換就是沿坐標軸縮放(Scale),這種變換可以改變模而且有可能改變方向。
\[\mathrm{scale}(s_x,s_y)=\begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix}
\]
\[\begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} s_xx \\ x_yy \end{bmatrix}
\]
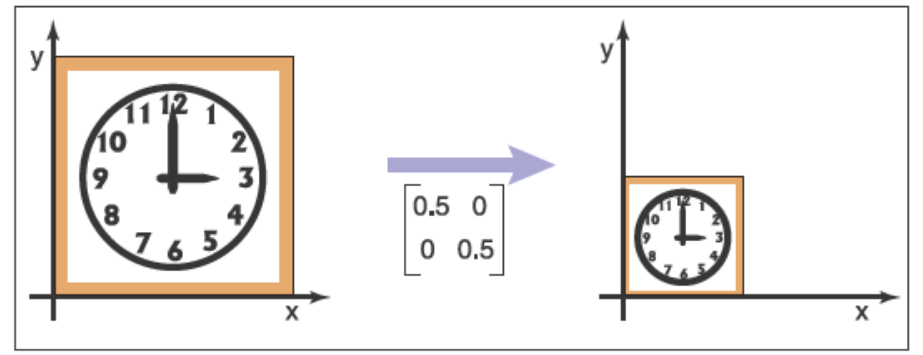
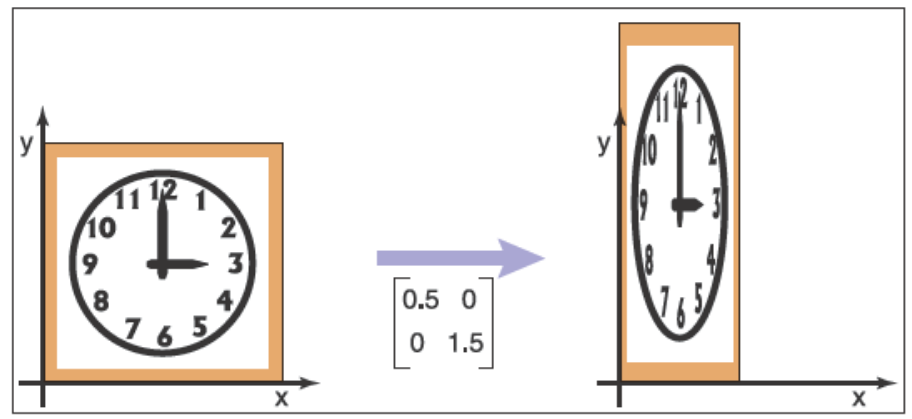
下面是兩個縮放的例子
\[\mathrm{scale}(0.5,0.5) = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix}
\]
![img]()
\[\mathrm{scale}(0.5,1.5) = \begin{bmatrix} 0.5 & 0 \\ 0 & 1.5 \end{bmatrix}
\]
![img]()
剪切(Shearing)
??剪切描述的是把東西推向某邊的那種變換,水平剪切矩陣和豎直剪切矩陣長這樣
\[\mathrm{shear-x}(s)=\begin{bmatrix} 1 & s \\ 0 & 1 \end{bmatrix},\mathrm{shear-y}(s)=\begin{bmatrix} 1 & 0 \\ s & 1 \end{bmatrix}
\]
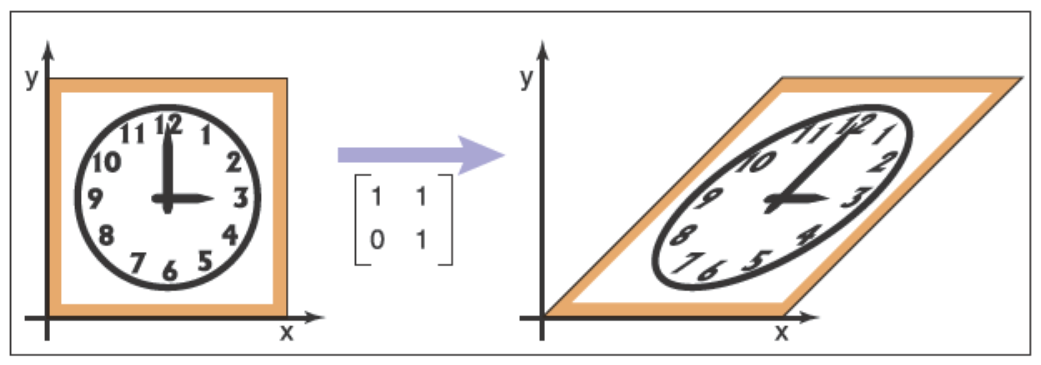
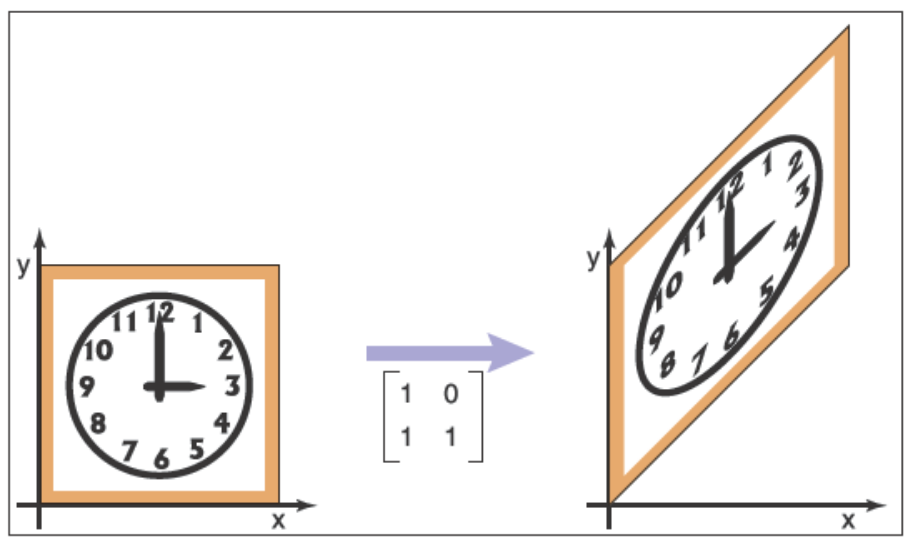
下面是兩個剪切的例子
\[\mathrm{shear-x}(1)=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}
\]
![img]()
\[\mathrm{shear-y}(1)=\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix}
\]
![img]()
旋轉(Rotation)
??假設我們想以一個\(\phi\)角度逆時針旋轉向量\(\mathbf{a}\)到向量\(\mathbf{b}\),我們首先用半徑\(r\)和角度\(\alpha\)來表示向量\(\mathbf{a}\)
\[x_a=r\cos\alpha
\]
\[y_a=r\sin\alpha
\]
因為\(\mathbf{b}\)是從\(\mathbf{a}\)旋轉得到的,因此可得
\[x_b=r\cos(\alpha+\phi)=r\cos\alpha\cos\phi-r\sin\alpha\sin\phi
\]
\[y_b=r\sin(\alpha+\phi)=r\sin\alpha\cos\phi+r\cos\alpha\sin\phi
\]
因為\(x_a=r\cos\alpha\)、\(y_a=r\sin\alpha\),這實際上等于
\[x_b=x_a\cos\phi-y_a\sin\phi
\]
\[y_b=y_a\cos\phi+x_a\sin\phi
\]
可以化成矩陣向量相乘形式
\[\begin{bmatrix} x_b \\ y_b \end{bmatrix} = \begin{bmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{bmatrix} \begin{bmatrix} x_a \\ y_a \end{bmatrix}
\]
因此旋轉矩陣為
\[\mathrm{rotate}(\phi) = \begin{bmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{bmatrix}
\]
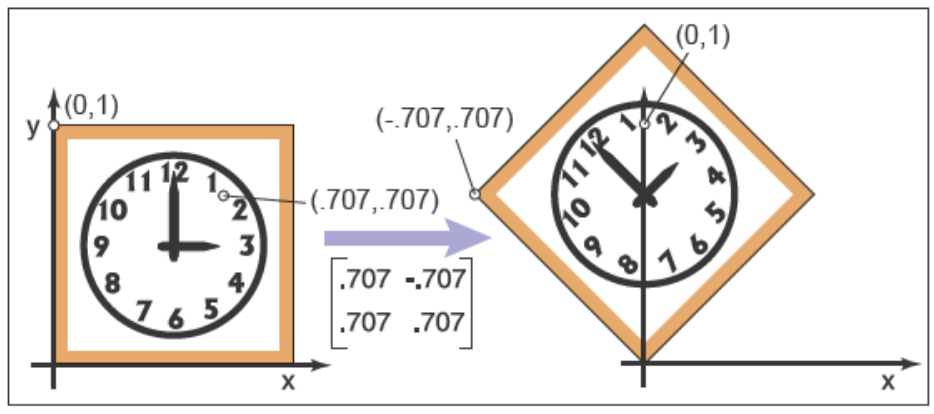
下面是兩個旋轉的例子
\[\begin{bmatrix} \cos\frac{\pi}{4} & -\sin\frac{\pi}{4} \\ \sin\frac{\pi}{4} & \cos\frac{\pi}{4} \end{bmatrix} = \begin{bmatrix} 0.707 & -0.707 \\ 0.707 & 0.707 \end{bmatrix}
\]
![img]()
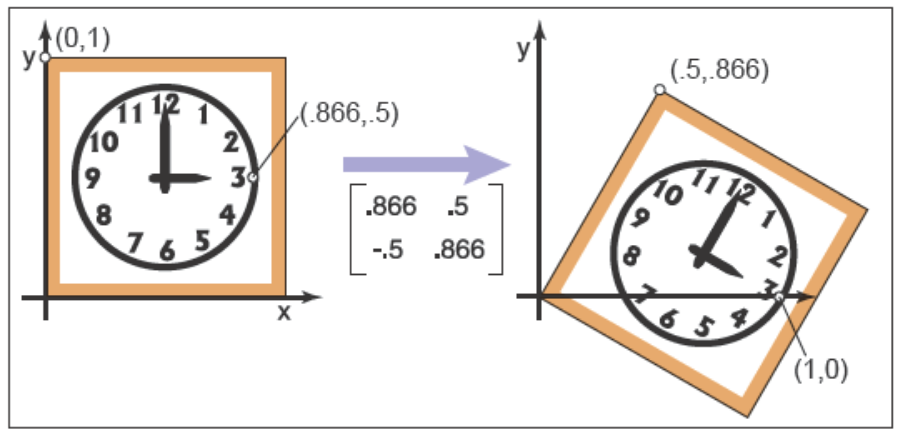
\[\begin{bmatrix} \cos\frac{-\pi}{6} & -\sin\frac{-\pi}{6} \\ \sin\frac{-\pi}{6} & \cos\frac{-\pi}{6} \end{bmatrix} = \begin{bmatrix} 0.866 & 0.5 \\ -0.5 & 0.866 \end{bmatrix}
\]
![img]()
反射(Reflection)
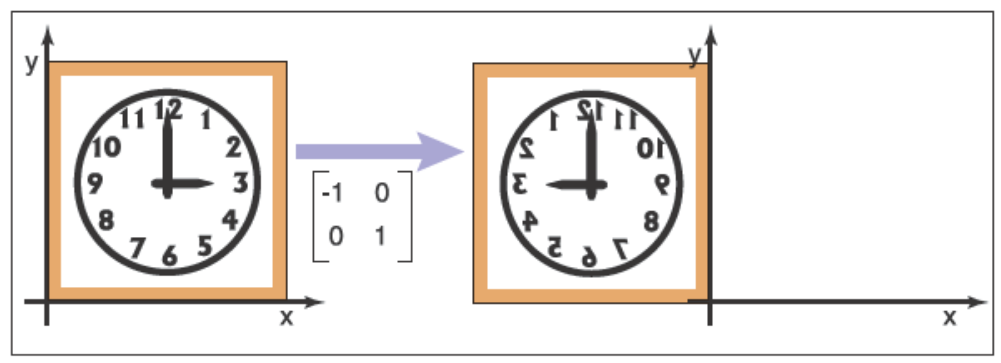
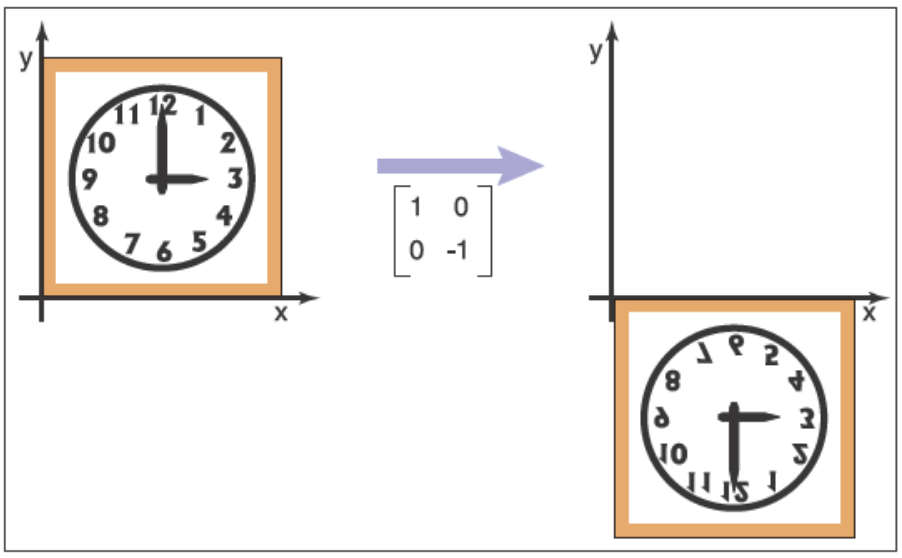
??我們可以讓向量沿著坐標軸反射,沿\(y\)軸反射和沿\(x\)軸反射的矩陣為
\[\mathrm{reflect-y}=\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix},\mathrm{reflect-x}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}
\]
下面是兩個反射的例子
![img]()
![img]()
要注意的是,疊加這兩種反射等效于旋轉\(\pi\)弧度。
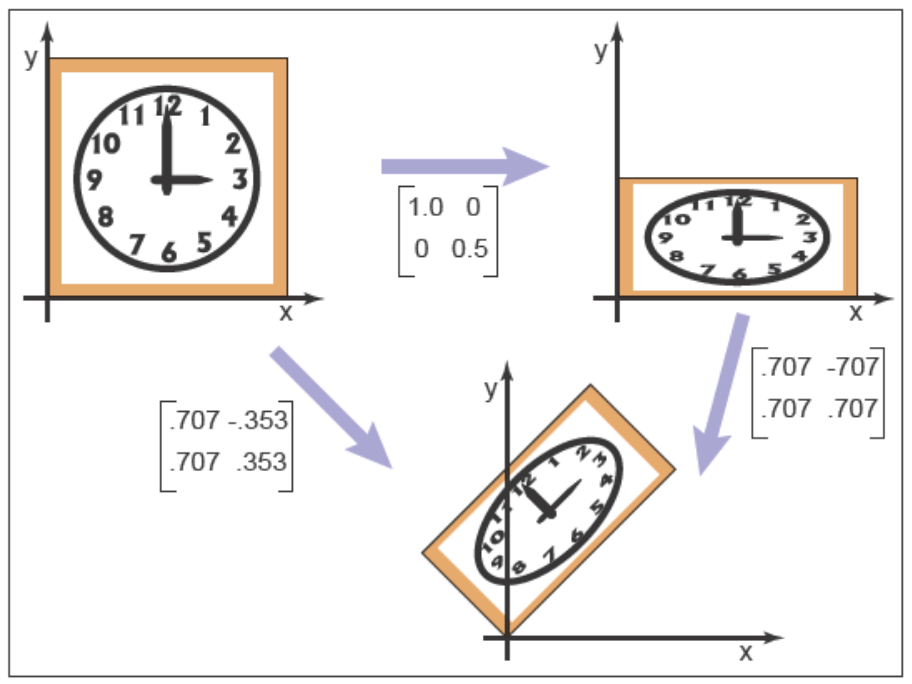
??對于圖形程序來說施加多個變換是很常見的,例如首先施加縮放\(\mathbf{S}\)接著施加旋轉\(\mathbf{R}\),可以通過兩步做到
\[\mathbf{v}_2=\mathbf{S}\mathbf{v}_1,\mathbf{v}_3=\mathbf{R}\mathbf{v}_2
\]
另一個方法是
\[\mathbf{v}_3 =\mathbf{R}(\mathbf{Sv}_1)
\]
因為矩陣相乘服從結合律我們也可以這么寫
\[\mathbf{v}_3 = (\mathbf{RS})\mathbf{v}_1
\]
這樣我們可以得到一個新的矩陣\(\mathbf{M}=\mathbf{RS}\),這個新的矩陣描述的就是先縮放再旋轉的變換。下圖是個相關的例子
![img]()
之前提到過矩陣相乘不服從交換律,下圖是個相關的例子
![img]()
??有時候需要撤銷變換,把變換分成更簡單的片段。例如,讓用戶控制旋轉因子和縮放因子來向其展示變換。但是在內部,變換可能僅僅使用一個矩陣來表達,而這個矩陣已經混合好了旋轉和縮放。其實可以通過先把矩陣拆解成期望的片段,接著調整這些片段,最后再次組裝這些變換得到。
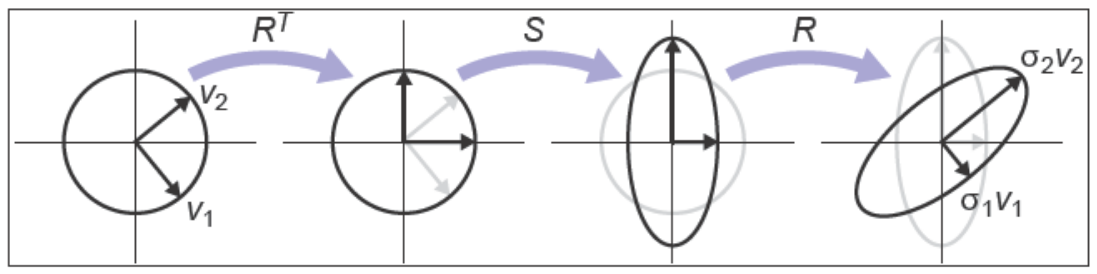
??對于對稱矩陣來說有特征值分解,可以把對稱矩陣\(\mathbf{A}\)分解成如下形式
\[\mathbf{A}=\mathbf{RSR}^\mathrm{T}
\]
式中的\(\mathbf{R}\)為正交矩陣,\(\mathbf{S}\)為對角矩陣。從幾何角度來理解,可以把\(\mathbf{R}\)當作旋轉,把\(\mathbf{S}\)當作縮放,實際上就是把單布變換\(\mathbf{A}\)變成了多步變換\(\mathbf{RSR}^\mathrm{T}\)。令特征向量為\(\mathbf{v}_1\)和\(\mathbf{v}_2\),特征值為\(\lambda_1\)和\(\lambda_2\),\(\mathbf{RSR}^\mathrm{T}\)代表的多步變換可以被解釋為
![img]()
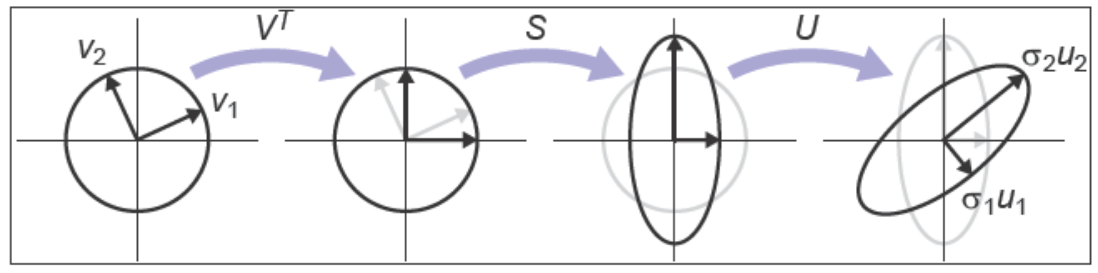
??對于非對稱矩陣來說有奇異值分解,可以把非對稱矩陣\(\mathbf{A}\)分解成如下形式
\[\mathbf{A}=\mathbf{USV}^\mathrm{T}
\]
式中的\(\mathbf{U}\)和\(\mathbf{V}\)為正交矩陣,\(\mathbf{S}\)為對角矩陣。從幾何的角度來理解,可以把\(\mathbf{U}\)和\(\mathbf{V}\)當作旋轉,把\(\mathbf{S}\)當作縮放。令左奇異向量為\(\mathbf{u}_1\)和\(\mathbf{u}_2\),右奇異向量為\(\mathbf{v}_1\)和\(\mathbf{v_2}\),奇異值為\(\sigma_1\)和\(\sigma_2\),\(\mathbf{USV}^\mathrm{T}\)代表的多步變換可以被解釋為
![img]()
??還有一種是用于非0旋轉的Paeth分解,如下所示
\[\begin{bmatrix} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{bmatrix} = \begin{bmatrix} 1 & \frac{\cos\phi-1}{\sin\phi} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ \sin\phi & 1 \end{bmatrix} \begin{bmatrix} 1 & \frac{\cos\phi-1}{\sin\phi} \\ 0 & 1 \end{bmatrix}
\]
以45°旋轉為例可以得到
\[\mathrm{rotate}(\frac{\pi}{4})=\begin{bmatrix} 1 & 1-\sqrt{2} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ \frac{\sqrt{2}}{2} & 1 \end{bmatrix} \begin{bmatrix} 1 & 1-\sqrt{2} \\ 0 & 1 \end{bmatrix}
\]
這種特別的變換對光柵旋轉非常有用,因為剪切是對圖像非常有效的光柵操作,它會引入一些鋸齒但是不會留下孔洞。一個關鍵的觀察是,如果取光柵位置\((i,j)\)接著施加水平剪切,我們可以得到
\[\begin{bmatrix} 1 & s \\ 0 & 1 \end{bmatrix} \begin{bmatrix} i \\ j \end{bmatrix} = \begin{bmatrix} i+sj \\ j \end{bmatrix}
\]
如果把\(sj\)舍入到最近的整數,這個量會讓每一行往側邊移動一點,行與行之間移動的量會相差一定量,但是相同行的每個位置往側邊移動的量是一樣的,因此能讓旋轉后的圖像的內部無孔洞。對于豎直剪切也是一樣的道理,因此我們可以簡單地實現一個光柵旋轉。
三維線性變換可以從二維線性變換推廣得到,例如沿軸縮放為
\[\mathrm{scale}(s_x,s_y,s_z)=\begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{bmatrix}
\]
三維中的旋轉分為繞z、x、y軸旋轉,分別為
\[\mathrm{rotate-z}(\phi)=\begin{bmatrix} \cos\phi & -\sin\phi & 0 \\ \sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{bmatrix}
\]
\[\mathrm{rotate-x}(\phi)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\phi & -\sin\phi \\ 0 & \sin\phi & \cos\phi \end{bmatrix}
\]
\[\mathrm{rotate-y}(\phi)=\begin{bmatrix} \cos\phi & 0 & \sin\phi \\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{bmatrix}
\]
在二維中的剪切可以沿著某個軸進行,而在三維中
\[\mathrm{shear-x}(d_x,d_z)=\begin{bmatrix} 1 & d_x & d_z \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
\]
和二維變換一樣,三維變換矩陣可以用奇異值分解,從而得到一個旋轉矩陣、一個縮放矩陣、另一個旋轉矩陣。當然了,對稱三維矩陣也可以使用特征值分解,從而得到一個旋轉矩陣、一個縮放矩陣、一個逆旋轉矩陣。此外,一個三維旋轉矩陣也可以分解成三維剪切矩陣的乘積。
任意三維旋轉(Arbitrary 3D Rotations)
??繞任意軸旋轉其實很簡單,可以利用上一章的對矩陣變換向量的不同理解得到。假設我們有一個點\((x,y,z)\)處于全局坐標系中,想讓點\((x,y,z)\)繞\(\mathbf{w}\)軸旋轉,我們首先得找到另外兩個輔助軸\(\mathbf{u}\)和\(\mathbf{v}\),要求是\(\mathbf{u}\)、\(\mathbf{v}\)、\(\mathbf{w}\)能組成一個標準正交基。有了這個條件后,我們先把點\((x,y,z)\)投影到\(\{\mathbf{u},\mathbf{v},\mathbf{w}\}\)這個坐標系中,于是可以使用這個矩陣
\[\begin{bmatrix} x_u & y_u & z_u \\ x_v & y_v & z_v \\ x_w & y_w & z_w \end{bmatrix}
\]
接著我們繞\(\{\mathbf{u},\mathbf{v},\mathbf{w}\}\)這個坐標系中的z軸旋轉,于是可以用這個矩陣
\[\mathrm{rotate-z}(\phi)=\begin{bmatrix} \cos\phi & -\sin\phi & 0 \\ \sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{bmatrix}
\]
最后我們使用\(\mathbf{u}\)、\(\mathbf{v}\)、\(\mathbf{w}\)這三個基向量,把在這個坐標系中繞z軸旋轉后的坐標變換到全局坐標系中,從而得到點\((x,y,z)\)繞\(\mathbf{w}\)軸旋轉后的點\((x^{new},y^{new},z^{new})\),因此可以使用這個矩陣
\[\begin{bmatrix} x_u & x_v & x_w \\ y_u & y_v & y_w \\ z_u & z_v & z_w \end{bmatrix}
\]
綜上,繞軸多步變換為
\[\begin{bmatrix} x^{new} \\ y^{new} \\ z^{new} \end{bmatrix} = \begin{bmatrix} x_u & x_v & x_w \\ y_u & y_v & y_w \\ z_u & z_v & z_w \end{bmatrix} \begin{bmatrix} \cos\phi & -\sin\phi & 0 \\ \sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_u & y_u & z_u \\ x_v & y_v & z_v \\ x_w & y_w & z_w \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}
\]
??絕大多數三維向量都是用來表示位置或方向的,例如光從哪來。不過有些向量會被用來表示表面法線(Surface Normals),當表面被變換時這些法線不能以同樣方式被變換。假設表面會被矩陣\(\mathbf{M}\)變換,表面的切向向量\(\mathbf{t}\)被\(\mathbf{M}\)變換后會保持與表面相切。然而表面法線\(\mathbf{n}\)被\(\mathbf{M}\)變換后可能不會與表面垂直。因此我們得以\(\mathbf{M}\)為基礎,得到用于變換法線的矩陣\(\mathbf{N}\)。因為表面的切向向量與表面法線總是垂直的,因此可以得到
\[\begin{align*}
\mathbf{n}^\mathrm{T}\mathbf{t}&=0 \\
\mathbf{n}^\mathrm{T}\mathbf{I}\mathbf{t}&=0 \\
\mathbf{n}^\mathrm{T}\mathbf{M}^{-1}\mathbf{M}\mathbf{t}&=0
\end{align*}
\]
這兩個向量被分別變換后也會保持垂直,因此
\[\begin{align*}
(\mathbf{Nn})^\mathrm{T}\mathbf{Mt}&=0 \\
\mathbf{n}^\mathrm{T}\mathbf{N}^\mathrm{T}\mathbf{Mt}&=0
\end{align*}
\]
由\(\mathbf{n}^\mathrm{T}\mathbf{M}^{-1}\mathbf{M}\mathbf{t}=0\)和\(\mathbf{n}^\mathrm{T}\mathbf{N}^\mathrm{T}\mathbf{Mt}=0\)可以得到\(\mathbf{N}^\mathrm{T}=\mathbf{M}^{-1}\),所以
\[\mathbf{N}=(\mathbf{M}^{-1})^\mathrm{T}或\mathbf{N}=(\mathbf{M}^\mathrm{T})^{-1}
\]
之前已經探討過了使用矩陣來進行縮放、旋轉、剪切等變換,在二維中變換為
\[\begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = \begin{bmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}
\]
這種變換有個缺點,就是不能移動物體,只能進行縮放、旋轉等變換。為了讓物體平移(Translate),我們必須實現這樣一種變換
\[\begin{align*}
x^{\prime} &= x + x_t \\
y^{\prime} &= y + y_t
\end{align*}
\]
結果很簡單,我們為表示位置的點\((x,y)\)增加一個坐標到\((x,y,1)\)接著與下面這種\(3 \times 3\)的矩陣相乘
\[\begin{bmatrix} m_{11} & m_{12} & x_t \\ m_{21} & m_{22} & y_t \\ 0 & 0 & 1 \end{bmatrix}
\]
相乘的結果為
\[\begin{bmatrix} x^{\prime} \\ y^{\prime} \\ 1 \end{bmatrix} = \begin{bmatrix} m_{11} & m_{12} & x_t \\ m_{21} & m_{22} & y_t \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} \equiv \begin{bmatrix} m_{11}x+m_{12}y+x_t \\ m_{21}x+m_{22}y+y_t \\ 1 \end{bmatrix}
\]
這一個矩陣就實現了一次線性變換加上一次平移變換,這種類型的變換叫做仿射變換(Affine Transformation),為實現仿射變換而增加的那一個維度的坐標叫做齊次坐標(Homogeneous Coordinate)。
??要注意的是,這種變換會帶來一個問題,使表示方向的向量平移是明顯不合理的,可以把齊次坐標置零解決這個問題
\[\begin{bmatrix} 1 & 0 & x_t \\ 0 & 1 & y_t \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 0 \end{bmatrix}
\]
在之后的章節,我們會實現透視視圖,到那個時候會了解齊次坐標的其它用途。特別地來說,齊次坐標是在圖形硬件中實現的渲染器的設計和操作的基石。在三維中的平移和二維中的差不多,增加一個第四坐標即可,因此平移變換為
\[\begin{bmatrix} 1 & 0 & 0 & x_t \\ 0 & 1 & 0 & y_t \\ 0 & 0 & 1 & z_t \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x+x_t \\ y+y_t \\ z+z_t \\ 1 \end{bmatrix}
\]
這里要再次注意把表示方向的向量的齊次坐標置零。
??有時我們可能想進行逆變換,例如對于縮放\(\mathrm{scale}(s_x,s_y,s_z)\)的逆縮放就是\(\mathrm{scale}(1/s_x,1/s_y,1/s_z)\),旋轉的逆就是反方向旋轉,平移的逆就是反方向平移。如果我們有一些矩陣\(\mathbf{M}=\mathbf{M}_1\mathbf{M}_2\cdots\mathbf{M}_n\),它的逆變換就是\(\mathbf{M}^{-1}=\mathbf{M}^{-1}_n\cdots\mathbf{M}^{-1}_2\mathbf{M}^{-1}_1\)。
??當然了,我們也可以用奇異值分解來求逆變換,對于上面的矩陣\(\mathbf{M}\)有
\[\mathbf{M}=\mathbf{R}_1\mathrm{scale}(\sigma_1,\sigma_2,\sigma_3)\mathbf{R}_2
\]
因此它的逆變換\(\mathbf{M}^{-1}\)為
\[\mathbf{M}^{-1}=\mathbf{R}^{\mathrm{T}}_2\mathrm{scale}(1/\sigma_1,1/\sigma_2,1/\sigma_3)\mathbf{R}^{\mathrm{T}}_1
\]
??之前的所有討論都是使用矩陣來變換一些點,不過這還隱藏著其它含義,其實我們也可以把它們看成是在改變坐標系統。例如坐在行進的車中觀察,這個時候會發現車之外的物體都在相對你往后移動,從計算機和變換的角度來理解,就是每幀都有變換矩陣作用于物體來讓其往后移動。從另一個方面來說,感受到相對移動實際上是以你的視角為參考的結果。這個時候就發現了變換矩陣和改變坐標系統實際上是息息相關的。
??從幾何上說,一個坐標系統或坐標幀是由原點和基構成的,標準正交基是最常用的一種。在一幀中,坐標系統的原點和基分別為\(\mathbf{p}\)和\(\{\mathbf{u},\mathbf{v},\mathbf{w}\}\),我們可以用在這個坐標系中的一點\((u,v,w)\)得到另外一點
\[\mathbf{p}+u\mathbf{u}+v\mathbf{v}+w\mathbf{w}
\]
在計算機中存儲這些向量時,會發現這些向量實際上是在某個坐標系統中表達的,例如坐標系原點\(\mathbf{p}\)實際上是位于某個坐標系統中的。為了讓這一切進行下去,我們需要指定規范坐標系統,通常叫“全局”或“世界”坐標系統,這種系統會被用來描述其它所有系統。
??在二維中,規范坐標系統通常用點\(\mathbf{o}\)表示原點,用\(\mathbf{x}\)和\(\mathbf{y}\)來表示右手標準正交基向量。其它的坐標系統可能用\(\mathbf{e}\)來表示原點,用\(\mathbf{u}\)和\(\mathbf{v}\)來表示右手標準正交基向量。一般來說,用于描述規范坐標系統的數據是不需要被顯式存儲的,因為它們是其它所有坐標系統的參考。使用規范坐標系中的坐標\((x_p,y_p)\)可以得到它在世界空間中的坐標為
\[\mathbf{p}=(x_p,y_p)\equiv\mathbf{o}+x_p\mathbf{x}+y_p\mathbf{y}
\]
使用某個坐標系中的坐標\((u_p,v_p)\)可以得到它在規范坐標系中的坐標為
\[\mathbf{p}=(u_p,v_p)\equiv\mathbf{e}+u_p\mathbf{u}+v_p\mathbf{v}
\]
因此,某個坐標系中的坐標\((u_p,v_p)\)和它在規范坐標系中的坐標\((x_p,y_p)\)的關系為
\[\begin{bmatrix} x_p \\ y_p \\ 1 \end{bmatrix} = \begin{bmatrix} x_u & x_v & x_e \\ y_u & y_v & y_e \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} u_p \\ v_p \\ 1 \end{bmatrix}
\]
讓它變簡潔點可以化簡成
\[\mathbf{p}_{xy}=\begin{bmatrix} \mathbf{u} & \mathbf{v} & \mathbf{e} \\ 0 & 0 & 1 \end{bmatrix} \mathbf{p}_{uv}
\]
我們稱等式右側的矩陣為幀到規范(Frame-To-Canonical)矩陣,它把在某個坐標系下的坐標轉化為在規范坐標系下的坐標。從另一個方向變換,我們可以得到
\[\begin{bmatrix} u_p \\ v_p \\ 1 \end{bmatrix} = \begin{bmatrix} x_u & y_u & 0 \\ x_v & y_v & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & -x_e \\ 0 & 1 & -y_e \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_p \\ y_p \\1 \end{bmatrix}
\]
讓它變簡潔點可以化簡成
\[\mathbf{p}_{uv}=\begin{bmatrix} \mathbf{u} & \mathbf{v} & \mathbf{e} \\ 0 & 0 & 1 \end{bmatrix}^{-1} \mathbf{p}_{xy}
\]
我們稱等式右側的矩陣為規范到幀(Canonical-To-Frame)矩陣,它把在規范坐標系下的坐標轉化為在某個坐標系下的坐標。因此在三維中我們有
\[\begin{align*}
\begin{bmatrix} x_p \\ y_p \\ z_p \\ 1 \end{bmatrix}&=\begin{bmatrix} 1 & 0 & 0 & x_e \\ 0 & 1 & 0 & y_e \\ 0 & 0 & 1 & z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_u & x_v & x_w & 0 \\ y_u & y_v & y_w & 0 \\ z_u & z_v & z_w & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} u_p \\ v_p \\ w_p \\1 \end{bmatrix} \\ \mathbf{p}_{xyz} &= \begin{bmatrix} \mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e} \\ 0 & 0 & 0 & 1 \end{bmatrix} \mathbf{p}_{uvw}
\end{align*}
\]
\[\begin{align*}
\begin{bmatrix} u_p \\ v_p \\ w_p \\ 1 \end{bmatrix} &= \begin{bmatrix} x_u & y_u & z_u & 0 \\ x_v & y_v & z_v & 0 \\ x_w & y_w & z_w & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_p \\ y_p \\ z_p \\ 1 \end{bmatrix} \\ \mathbf{p}_{uvw} &= \begin{bmatrix} \mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e} \\ 0 & 0 & 0 & 1 \end{bmatrix}^{-1} \mathbf{p}_{xyz}
\end{align*}
\]




 浙公網安備 33010602011771號
浙公網安備 33010602011771號