開篇
??也許,圖形程序中最通用的的工具就是那些用來變換(Transform)點和向量的矩陣,這章主要講的是線性代數的基礎知識。
行列式(Determinants)
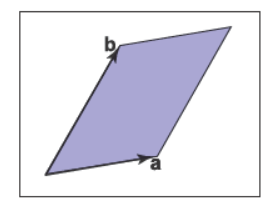
??我們一般可能會想行列式會在線性方程組的解中出現,不過可以先以向量相乘的方式來思考行列式。對于二維向量來說,行列式\(|\mathbf{a}\mathbf{b}|\)是由向量\(\mathbf{a}\)和向量\(\mathbf{b}\)圍成的平行四邊形的面積決定的,如下圖所示。
![img]()
不過這個面積是有符號的,如果是右手的那么為正,反之則為負,因此我們可以得到\(|\mathbf{a}\mathbf{b}|=-|\mathbf{b}\mathbf{a}|\)。這里的“右手的”可以理解為當逆時針旋轉第一個向量時,它和第二個向量的夾角會變小。在三維中,行列式要用到三個向量,對于三個向量\(\mathbf{a}\)、\(\mathbf{b}\)、\(\mathbf{c}\)來說,行列式\(|\mathbf{a}\mathbf{b}\mathbf{c}|\)是由這三個向量圍成的平行六面體的有符號容積決定的。
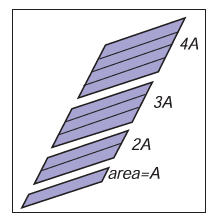
??為了計算二階行列式,我們首先可以了解下它的相關性質,縮放某個向量會縮放平行四邊形的面積,因此可以得到
\[|(k\mathbf{a})\mathbf{b}|=|\mathbf{a}(k\mathbf{b})|=k|\mathbf{a}\mathbf{b}|
\]
![img]()
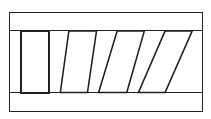
剪切平行四邊形不會改變它的面積,因此
\[|(\mathbf{a}+k\mathbf{b})\mathbf{b}|=|\mathbf{a}(\mathbf{b}+k\mathbf{a})|=|\mathbf{a}\mathbf{b}|
\]
![img]()
假設我們用笛卡爾坐標來表示\(\mathbf{a}\)和\(\mathbf{b}\),行列式\(|\mathbf{ab}|\)可以如下計算
\[\begin{align*}
|\mathbf{ab}| &= |(x_a\mathbf{x}+y_a\mathbf{y})(x_b\mathbf{x}+y_b\mathbf{y})| \\
&=x_ax_b|\mathbf{xx}|+x_ay_b|\mathbf{xy}|+y_ax_b|\mathbf{yx}|+y_ay_b|\mathbf{yy}| \\
&=x_ax_b(0)+x_ay_b(+1)+y_ax_b(-1)+y_ay_b(0)\\
&=x_ay_b-y_ax_b
\end{align*}
\]
因此在三維中
\[\begin{align*}
|\mathbf{abc}| &= |(x_a\mathbf{x}+y_a\mathbf{y}+z_a\mathbf{z})(x_b\mathbf{x}+y_b\mathbf{y}+z_b\mathbf{z})(x_c\mathbf{x}+y_c\mathbf{y}+z_c\mathbf{z})| \\
&=x_ay_bz_c-x_az_by_c-y_ax_bz_c+y_az_bx_c+z_ax_by_c-z_ay_bx_c
\end{align*}
\]
矩陣(Matrices)
??一個矩陣是遵循某些算術規則的數值元素數組,一個兩行三列的矩陣可以如下所示
\[\begin{bmatrix}
1.7 & -1.2 & 4.2 \\ 3.0 & 4.5 & -7.2
\end{bmatrix}
\]
矩陣算數(Matrix Arithmetic)
對于給定的矩陣,乘以一個常數可以得到
\[2 \begin{bmatrix}1 & -4 \\ 3 & 2 \end{bmatrix} = \begin{bmatrix} 2 & -8 \\ 6 & 4 \end{bmatrix}
\]
兩個矩陣求和可以得到
\[\begin{bmatrix} 1 & -4 \\ 3 & 2 \end{bmatrix} + \begin{bmatrix} 2 & 2 \\ 2 & 2 \end{bmatrix} = \begin{bmatrix} 3 & -2 \\ 5 & 4 \end{bmatrix}
\]
兩個矩陣相乘可以得到
\[\begin{bmatrix} a_{11} & \cdots & a_{1m} \\ \vdots && \vdots \\ \boxed{a_{i1}} & \boxed{\cdots} & \boxed{a_{im}} \\ \vdots && \vdots \\ a_{r1} & \cdots & a_{rm} \end{bmatrix} \begin{bmatrix} b_{11} & \cdots & \boxed{b_{1j}} & \cdots & b_{1c} \\ \vdots && \boxed{\vdots} && \vdots \\ b_{m1} & \cdots & \boxed{b_{mj}} & \cdots & n_{mc} \end{bmatrix} = \begin{bmatrix} p_{11} & \cdots & p_{1j} & \cdots & p_{1c} \\ \vdots && \vdots && \vdots \\ p_{i1} & \cdots & \boxed{p_{ij}} & \cdots & p_{ic} \\ \vdots && \vdots && \vdots \\ p_{r1} & \cdots & p_{rj} & \cdots & p_{rc} \end{bmatrix}
\]
\[p_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots+a_{im}b_{mj}
\]
下面是個矩陣相乘的例子
\[\begin{bmatrix} 0 & 1 \\ 2 & 3 \\ 4 & 5 \end{bmatrix} \begin{bmatrix} 6 & 7 & 8 & 9 \\ 0 & 1 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 2 & 3 \\ 12 & 17 & 22 & 27 \\ 24 & 33 & 42 &51 \end{bmatrix}
\]
要注意的是矩陣相乘不服從交換律,因此
\[\mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A}
\]
而且如果已知\(\mathbf{A}\mathbf{B} = \mathbf{A}\mathbf{C}\),矩陣\(\mathbf{B}\)有可能不會等于矩陣\(\mathbf{C}\)。不過幸運的是矩陣相乘服從結合律和分配律,因此
\[\begin{align*}
\mathbf{(AB)C}&=\mathbf{A(BC)}\\
\mathbf{A(B+C)}&=\mathbf{AB+AC}\\
\mathbf{(A+B)C}&=\mathbf{AC+BC}
\end{align*}
\]
矩陣中的操作(Operation on Matrices)
??對于一個矩陣來說我們可能會考慮到它的逆,就像對于實數\(x\)來說的\(1/x\)一樣。實數\(x\)乘以它的逆\(1/x\)為實數\(1\),那么矩陣\(\mathbf{A}\)乘以它的逆\(\mathbf{A}^{-1}\),應該等于“矩陣\(1\)”。這種矩陣只在方塊矩陣中出現,它被稱為單位矩陣(Identity Matrix)。這個矩陣的對角線上的元素為\(1\)其它元素為\(0\),比如
\[\mathbf{I} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
\]
因此\(\mathbf{A}\mathbf{A}^{-1}=\mathbf{I}\),下面是個矩陣求逆的例子
\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}^{-1} = \begin{bmatrix} -2.0 & 1.0 \\ 1.5 & -0.5 \end{bmatrix}
\]
因為
\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} -2.0 & 1.0 \\ 1.5 & -0.5 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
\]
此外矩陣的逆還有如下性質
\[(\mathbf{AB})^{-1}=\mathbf{B^{-1}A^{-1}}
\]
一個矩陣的轉置\(\mathbf{A^{\mathrm{T}}}\)和\(\mathbf{A}\)有相同的數字,不過是\(\mathbf{A}\)行列交換后的結果,因此
\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}^{\mathrm{T}} = \begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 &6 \end{bmatrix}
\]
矩陣的轉置有如下性質
\[\mathbf{(AB)}^{\mathrm{T}}=\mathbf{B^{\mathrm{T}}A^{\mathrm{T}}}
\]
矩陣的行列式就是把矩陣的括號替換成豎線,有如下性質
\[|\mathbf{AB}|=|\mathbf{A}||\mathbf{B}|
\]
\[|\mathbf{A}^{-1}|=\frac{1}{|\mathbf{A}|}
\]
\[|\mathbf{A}^{\mathrm{T}}|=|\mathbf{A}|
\]
??有時候我們有可能想旋轉一個二維向量\(\mathbf{a}=(x_a,y_a)90°\)到\(\mathbf{a}^{\prime}=(-y_a,x_a)\),可以使用一個\(2 \times 2\)的矩陣乘以一個\(2 \times 1\)的矩陣來表示這一變換,這個\(2 \times 1\)的矩陣叫做列向量(Column Vector),因此
\[\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} x_a \\ y_a \end{bmatrix} = \begin{bmatrix} -y_a \\ x_a \end{bmatrix}
\]
我們也可以使用行向量和上式的矩陣的轉置相乘來得到這一變換
\[\begin{bmatrix} x_a & y_a \end{bmatrix} \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} = \begin{bmatrix} -y_a & x_a \end{bmatrix}
\]
此外我們也可以用矩陣相乘來得到向量點乘的結果,假設有列向量\(\mathbf{a}\)和\(\mathbf{b}\),可以得到
\[\mathbf{a} \cdot \mathbf{b} = \mathbf{a}^{\mathrm{T}} \mathbf{b}
\]
以三維向量的點積為例,可以得到
\[\begin{bmatrix} x_a & y_a & z_a \end{bmatrix} \begin{bmatrix} x_b \\ y_b \\ z_b \end{bmatrix} = \begin{bmatrix} x_ax_b + y_ay_b + z_az_b \end{bmatrix}
\]
對于\(\mathbf{ab^{\mathrm{T}}}\)的情況我們也可以了解下,這個時候
\[\begin{bmatrix} x_a \\ y_a \\ z_a \end{bmatrix} \begin{bmatrix} x_b & y_b & z_b \end{bmatrix} = \begin{bmatrix} x_ax_b & x_ay_b & x_az_b \\ y_ax_b & y_ay_b & y_az_b \\ z_ax_b & z_ay_b & z_az_b \end{bmatrix}
\]
其實我們還可以從不同的角度看待矩陣變換向量和點,接下來以\(3 \times 3\)的矩陣變換為例,對于\(\mathbf{y}=\mathbf{Ax}\)我們可知
\[\begin{bmatrix} | \\ \mathbf{y} \\ | \end{bmatrix} = \begin{bmatrix} - & \mathbf{r}_1 & - \\ - & \mathbf{r}_2 & - \\ - & \mathbf{r}_3 & - \end{bmatrix} \begin{bmatrix} | \\ \mathbf{x} \\ | \end{bmatrix}
\]
\[y_i = \mathbf{r}_i \cdot \mathbf{x}
\]
\(\mathbf{y}\)的第\(i\)個分量實際上是矩陣的第\(i\)個行向量和\(\mathbf{x}\)點積的結果,這實際上就是把\(\mathbf{x}\)投影到了\(\{\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3\}\)這個坐標系中,且投影的結果為\(\mathbf{y}\)。此外從另一個角度我們還可以知道
\[\begin{bmatrix} | \\ \mathbf{y} \\ | \end{bmatrix} = \begin{bmatrix} | & | & | \\ \mathbf{c}_1 & \mathbf{c}_2 & \mathbf{c}_3 \\ | & | & | \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}
\]
\[\mathbf{y}=x_1\mathbf{c}_1+x_2\mathbf{c}_2+x_3\mathbf{c}_3
\]
這實際上就是以\(\mathbf{c}_1\)、\(\mathbf{c}_2\)、\(\mathbf{c}_3\)為基向量建立坐標系,并且以在這個坐標系中的坐標\((x_1,x_2,x_3)\)得到\(\mathbf{y}\)。上述的兩個角度提供了獨到的見解來了解\(\mathbf{y}=\mathbf{Ax}\)這一抽象操作中的幾何含義。
矩陣的特殊類型(Special Types of Matrices)
??矩陣有些特殊的類型,比如單位矩陣就是對角矩陣(Diagonal Matrix),這種矩陣的非零元素只出現在對角線上。此外單位矩陣的轉置等于它本身,這種有對稱性的矩陣就叫做對稱矩陣(Symmetric Matrix)。最后單位矩陣還是正交矩陣(Orthogonal Matrix),因為這種矩陣的每一列的向量與它當中的其它列向量都相互垂直。正交矩陣的行列式非\(+1\)即\(-1\),而且有個非常好的性質
\[\mathbf{R}^\mathrm{T}\mathbf{R}=\mathbf{I}=\mathbf{R}\mathbf{R}^\mathrm{T}
\]
利用之前提到過的對矩陣變換向量的理解可以很容易得到這個結論,下面有些矩陣的例子
\[\begin{bmatrix} 8 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 9 \end{bmatrix}
\]
這個矩陣是對角矩陣也是對稱矩陣,不是正交矩陣
\[\begin{bmatrix} 1 & 1 & 2 \\ 1 & 9 & 7 \\ 2 & 7 & 1 \end{bmatrix}
\]
這個矩陣是對稱矩陣,不是對角矩陣也不是正交矩陣
\[\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix}
\]
這個矩陣是正交矩陣,不是對角矩陣也不是對稱矩陣
使用矩陣和行列式計算(Computing with Matrices and Determinants)
??之前的部分提到,取n個n維向量的行列式,是由這n個n維向量定義的n維平行體的n維有符號容積決定的,對于二維來說就是由向量圍成的平行四邊形的面積。我們可以使用矩陣解決行列式計算的機制,假設有二維向量\(\mathbf{r}\)和\(\mathbf{s}\),我們表示行列式為\(|\mathbf{r} \mathbf{s}|\),它的值是由向量圍成的平行四邊形的有符號面積。假設有笛卡爾坐標的兩個二維向量\((a,b)\)、\((A,B)\),行列式可以這么寫
\[\begin{vmatrix} \begin{bmatrix} a \\ b \end{bmatrix} \begin{bmatrix} A \\ B \end{bmatrix} \end{vmatrix} \equiv \begin{vmatrix} a & A \\ b & B \end{vmatrix} = aB-Ab
\]
??最開始的部分提到用暴力展開計算行列式,不過使用那個方法計算會遇到許多\(0\)系數,而且還會遇到很多正負號,行列式計算的一個標準方法就是拉普拉斯展開(Laplace's Expansion),使用這個方法計算的關鍵就是找到余子式(Cofactor),方塊矩陣的每個元素都有一個余子式,這個余子式是當前方塊矩陣少一行少一列的行列式,而且每個余子式的符號由所屬元素所在的行和列決定,如果行列相加為偶符號為正反之為負,因此可以得到符號矩陣
\[\begin{bmatrix} + & - & + & - & \cdots \\ - & + & - & + & \cdots \\ + & - & + & - & \cdots \\ - & + & - & + & \cdots \\ \vdots & \vdots & \vdots & \vdots & \ddots \end{bmatrix}
\]
對于下面的\(4 \times 4\)矩陣來說
\[\mathbf{A}=\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix}
\]
第一行的余子式是
\[a^{c}_{11} = \begin{vmatrix} a_{22} & a_{23} & a_{24} \\ a_{32} & a_{33} & a_{34} \\ a_{42} & a_{43} & a_{44} \end{vmatrix},a^{c}_{12} = - \begin{vmatrix} a_{21} & a_{23} & a_{24} \\ a_{31} & a_{33} & a_{34} \\ a_{41} & a_{43} & a_{44} \end{vmatrix} , a^{c}_{13} = \begin{vmatrix} a_{21} & a_{22} & a_{24} \\ a_{31} & a_{32} & a_{34} \\ a_{41} & a_{42} & a_{44} \end{vmatrix},a^{c}_{14} = - \begin{vmatrix} a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \end{vmatrix}
\]
矩陣的行列式就是累加某列或某行的每個元素與它們的余子式的乘積,以第二列為例
\[|\mathbf{A}| = a_{12}a^{c}_{12} + a_{22}a^{c}_{22} + a_{32}a^{c}_{32} + a_{42}a^{c}_{42}
\]
剩下要做的就是展開\(a^{c}_{12}\)、\(a^{c}_{22}\)、\(a^{c}_{32}\)、\(a^{c}_{42}\)以及后續的余子式。
計算逆(Computing Inverse)
??行列式的標準計算方法也給了我們一個工具來計算矩陣的逆,通過上個部分的拉普拉斯展開,我們可以知道一個\(4 \times 4\)的矩陣\(\mathbf{A}\)的逆\(\mathbf{A}^{-1}\)為
\[\mathbf{A}^{-1} = \frac{1}{|\mathbf{A}|} \begin{bmatrix} a^{c}_{11} & a^{c}_{21} & a^{c}_{31} & a^{c}_{41} \\ a^{c}_{12} & a^{c}_{22} & a^{c}_{32} & a^{c}_{42} \\ a^{c}_{13} & a^{c}_{23} & a^{c}_{33} & a^{c}_{43} \\ a^{c}_{14} & a^{c}_{24} & a^{c}_{34} & a^{c}_{44} \end{bmatrix}
\]
等式右側的矩陣實際上是把矩陣的每個元素替換成它的余子式所得到的矩陣的轉置,把它與\(\mathbf{A}\)相乘可得到對角線上的元素為
\[\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\
\cdot & \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot \end{bmatrix} \begin{bmatrix} a^{c}_{11} & \cdot & \cdot & \cdot \\ a^{c}_{12} & \cdot & \cdot & \cdot \\ a^{c}_{13} & \cdot & \cdot & \cdot \\ a^{c}_{14} & \cdot & \cdot & \cdot \\ \end{bmatrix} = \begin{bmatrix} |\mathbf{A}| & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \end{bmatrix}
\]
非對角線上的元素為
\[\begin{bmatrix} \cdot & \cdot & \cdot & \cdot \\ a_{21} & a_{22} & a_{23} & a_{24} \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \end{bmatrix} \begin{bmatrix} a^{c}_{11} & \cdot & \cdot & \cdot \\ a^{c}_{12} & \cdot & \cdot & \cdot \\ a^{c}_{13} & \cdot & \cdot & \cdot \\ a^{c}_{14} & \cdot & \cdot & \cdot \\ \end{bmatrix} = \begin{bmatrix} \cdot & \cdot & \cdot & \cdot \\ 0 & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \end{bmatrix}
\]
因為可以從\(a_{21}a^{c}_{11} + a_{22}a^{c}_{12} + a_{23}a^{c}_{13} + a_{24}a^{c}_{14}\)得到另外一個矩陣
\[\mathbf{B}=\begin{bmatrix} a_{21} & a_{22} & a_{23} & a_{24} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix}
\]
這個矩陣是奇異的,因此它的行列式\(a_{21}a^{c}_{11} + a_{22}a^{c}_{12} + a_{23}a^{c}_{13} + a_{24}a^{c}_{14}\)求出來為\(0\)。
線性系統(Linear Systems)
有時我們可能會遇到由\(n\)個等式\(n\)個未知量組成的線性方程組,以\(n=3\)為例
\[\begin{align*}
&3x+7y+2z=4 \\
&2x-4y-3z=-1 \\
&5x+2y+z=1
\end{align*}
\]
我們可以寫成如下形式
\[\begin{bmatrix} 3 & 7 & 2 \\ 2 & -4 & -3 \\ 5 & 2 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 4 \\ -1 \\ 1 \end{bmatrix}
\]
使用克拉默法則(Cramer's rule)可以得到
\[x = \frac{\begin{vmatrix} 4 & 7 & 2 \\ -1 & -4 & -3 \\ 1 & 2 & 1 \end{vmatrix}}{\begin{vmatrix} 3 & 7 & 2 \\ 2 & -4 & -3 \\ 5 & 2 & 1 \end{vmatrix}},y = \frac{\begin{vmatrix} 3 & 4 & 2 \\ 2 & -1 & -3 \\ 5 & 1 & 1 \end{vmatrix}}{\begin{vmatrix} 3 & 7 & 2 \\ 2 & -4 & -3 \\ 5 & 2 & 1 \end{vmatrix}},z = \frac{\begin{vmatrix} 3 & 7 & 4 \\ 2 & -4 & -1 \\ 5 & 2 & 1 \end{vmatrix}}{\begin{vmatrix} 3 & 7 & 2 \\ 2 & -4 & -3 \\ 5 & 2 & 1 \end{vmatrix}}
\]
這里要注意的是分母也就是矩陣的行列式\(|\mathbf{A}|\)不能為\(0\),如果為\(0\)那么意味著方程沒有唯一解。
特征值和矩陣對角化(Eigenvalues and Matrix Diagonalization)
??有些方塊矩陣有特征值(Eigenvalues)和特征向量(Eigenvectors),特征向量是非零的且與矩陣相乘時方向不變,現有矩陣\(\mathbf{A}\)和向量\(\mathbf{a}\),可以得到
\[\mathbf{Aa}=\lambda\mathbf{a}
\]
公式中的\(\lambda\)就是和特征向量關聯的特征值,矩陣的特征值和特征向量在很多應用中很有用。接下來先為矩陣求特征值和特征向量。我們有\(\mathbf{Aa}=\lambda\mathbf{a}\),因此可以得到
\[\mathbf{Aa}=\lambda\mathbf{Ia}
\]
這里的\(\mathbf{I}\)為單位矩陣,因此可以得到
\[\begin{align*}
\mathbf{Aa}-\lambda\mathbf{Ia} &=0 \\
(\mathbf{A}-\lambda\mathbf{I})\mathbf{a} &=0
\end{align*}
\]
因為\(\mathbf{a}\)不為\(0\)向量,所以\(\mathbf{A}-\lambda\mathbf{I}\)為奇異矩陣,這就使得它的行列式為\(0\),因此我們可以計算出特征值\(\lambda\),求出特征值\(\lambda\)后可以利用\((\mathbf{A}-\lambda\mathbf{I})\mathbf{a}=0\)為每個特征值\(\lambda\)求出關聯的特征向量\(\mathbf{a}\)。
??有一個非常重要的特殊情況就是當矩陣為對稱矩陣時,它的特征值和特征向量很簡單,而且這種矩陣可以對角化變成如下形式
\[\mathbf{A}=\mathbf{QDQ}^\mathrm{T}
\]
這里的\(\mathbf{Q}\)是正交矩陣,\(\mathbf{D}\)是對角矩陣。\(\mathbf{Q}\)的每一列是特征向量,\(\mathbf{D}\)的對角線上的元素是\(\mathbf{A}\)的特征值。把\(\mathbf{A}\)以這種形式分解就叫做特征值分解(Eigenvalue Decomposition),因為這樣分解能揭示矩陣的特征向量和特征值。下面以一個\(2 \times 2\)的對稱矩陣為例。
給定矩陣
\[\mathbf{A} = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix}
\]
可以得到
\[\lambda^{2}-3\lambda+1=0
\]
可以解出\(\lambda\)為
\[\lambda = \frac{3 \pm \sqrt{5}}{2}, \approx \begin{bmatrix} 2.618 \\ 0.382 \end{bmatrix}
\]
把\(\lambda=2.618\)帶入\((\mathbf{A}-\lambda\mathbf{I})\mathbf{a} =0\)可得
\[\begin{bmatrix} 2-2.618 & 1 \\ 1 & 1-2.618 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
\]
特征向量約等于\((0.8507,0.5257)\),對于另一個特征值\(\lambda = 0.382\),與它關聯的特征向量為\((-0.5257,0.8507)\),因此可以把\(\mathbf{A}\)分解為
\[\begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 0.8507 & -0.5257 \\ 0.5257 & 0.8507 \end{bmatrix} \begin{bmatrix} 2.618 & 0 \\ 0 & 0.382 \end{bmatrix} \begin{bmatrix} 0.8507 & 0.5257 \\ -0.5257 & 0.8507 \end{bmatrix}
\]
奇異值分解(Singular Value Decomposition)
??通過上一個部分我們可以知道對稱矩陣可以被對角化,然而我們遇到的大部分矩陣可能都不是對稱的,因此有個更加通用的方法叫奇異值分解(Singular Value Decomposition,SVD),使用這個方法可以把矩陣分解為
\[\mathbf{A}=\mathbf{USV}^\mathrm{T}
\]
其中\(\mathbf{U}\)和\(\mathbf{V}\)是可能不同的正交矩陣,前者的每列是\(\mathbf{A}\)的左奇異向量,后者的每列是\(\mathbf{A}\)的右奇異向量。\(\mathbf{S}\)是對角矩陣,對角線上面的每個元素是\(\mathbf{A}\)的奇異值。為了得到奇異值和奇異向量,我們可以在\(\mathbf{A}\)的基礎上構造對稱矩陣\(\mathbf{M}\)
\[\mathbf{M}=\mathbf{AA}^\mathrm{T}=(\mathbf{USV}^\mathrm{T})(\mathbf{USV}^\mathrm{T})^{\mathrm{T}}=\mathbf{US(V^{\mathrm{T}}V)SU^{\mathrm{T}}}=\mathbf{US}^{2}\mathbf{U}^\mathrm{T}
\]
接下來可以通過\(\mathbf{M}\)求出\(\mathbf{U}\)和\(\mathbf{S}\)接著利用\(\mathbf{A}=\mathbf{USV}^\mathrm{T}\)求出\(\mathbf{V}\),以下面的矩陣為例
\[\mathbf{A}=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix},\mathbf{M}=\mathbf{AA}^\mathrm{T}=\begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix}
\]
由上個部分的計算可以得到
\[\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 0.8507 & -0.5257 \\ 0.5257 & 0.8507 \end{bmatrix} \begin{bmatrix} \sqrt{2.618} & 0 \\ 0 & \sqrt{0.382} \end{bmatrix} \mathbf{V}^\mathrm{T}
\]
那么
\[\mathbf{V}=(\mathbf{S}^{-1}\mathbf{U}^\mathrm{T}\mathbf{A})^\mathrm{T}
\]
因此
\[\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} =\mathbf{U} \begin{bmatrix} \sigma_{1} & 0 \\ 0 & \sigma_{2} \end{bmatrix} \mathbf{V}^\mathrm{T} = \begin{bmatrix} 0.8507 & -0.5257 \\ 0.5257 & 0.8507 \end{bmatrix} \begin{bmatrix} 1.618 & 0 \\ 0 & 0.618 \end{bmatrix} \begin{bmatrix} 0.5257 & 0.8507 \\ -0.8507 & 0.5257 \end{bmatrix}
\]
式中的\(\sigma_{i}\)是矩陣的第\(i\)個奇異值的標準符號。



 浙公網安備 33010602011771號
浙公網安備 33010602011771號