物理強基課

• 有人聽強基課是聽提高，有人聽強基課是聽水題，有人聽強基課是聽新課，怎么回事呢？

彈簧

類SHM

• SHM 中，都可以規約成 \(E_p=\dfrac{1}{2}kx^2,E_k=\dfrac{1}{2}mv^2\)

例1

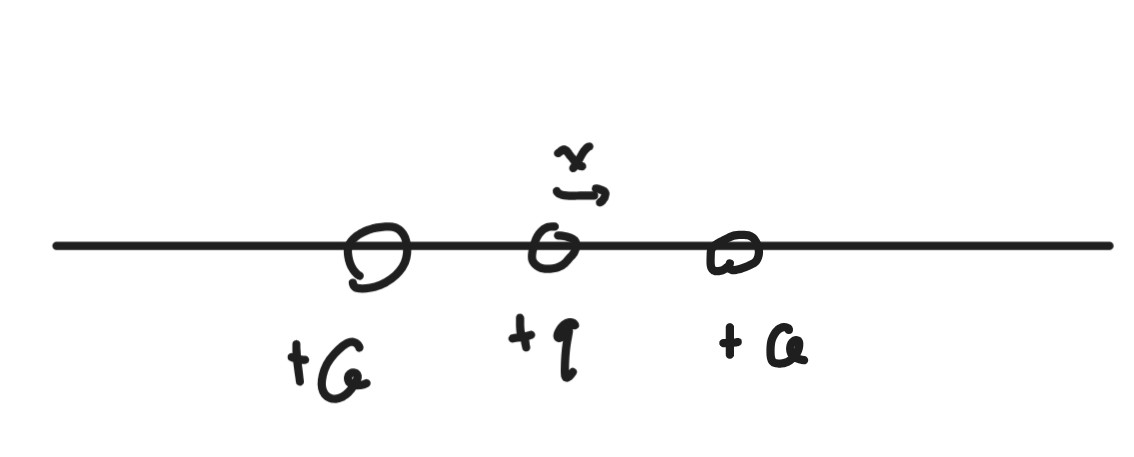
\(Q\) 固定，\(q\) 穿在絕緣光滑桿，總長 \(l\)，一個小移動 \(x\)，\(x<<l\)

• Trick：\((1+x)^n=1+nx(x<<1)\)

例2

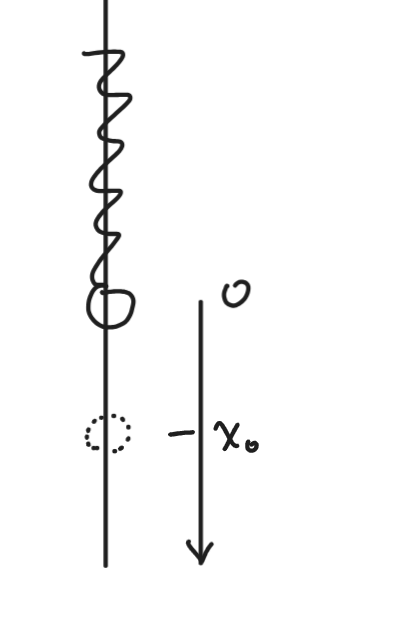
例3

原長為勢能 \(0\) 點，一個小的變化量 \(x\)

類簡諧運動？配方高妙

蹦極類型

從初中就開始學習了，加上一些圖像讓做題更簡單（復雜）

\(a-x\) 圖像

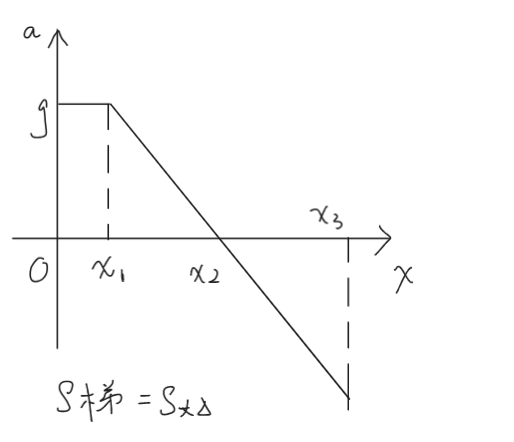
圖片少了個 \(a_m\)，為 \(x_3\) 對應的縱坐標

\(v:\dfrac{v^2}{2}-0=\dfrac{1}{2}(x_1+x_2)g\)

\(a_m:\dfrac{a_m}{g}=\sqrt{\dfrac{S_b}{S_s}}=\sqrt{\dfrac{\dfrac{1}{2}(x_1+x_2)g}{\dfrac{1}{2}(x_2-x_1)g}}=\sqrt{\dfrac{x_1+x_2}{x_2-x_1}}\)

\(x_3:\dfrac{1}{2}(x_1+x_2)g=\dfrac{1}{2}(x_3-x_2)a_m\)

\(x_3:mg=k(x2-x1),mgx_3=\dfrac{1}{2}k(x_3-x_1)^2\)

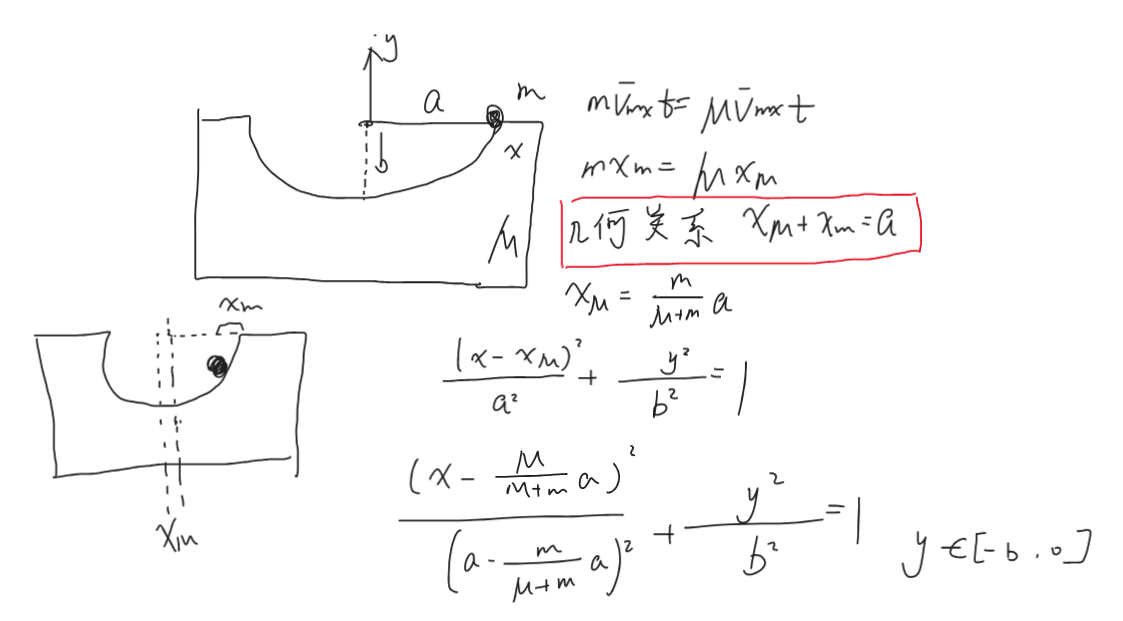
兩體模型

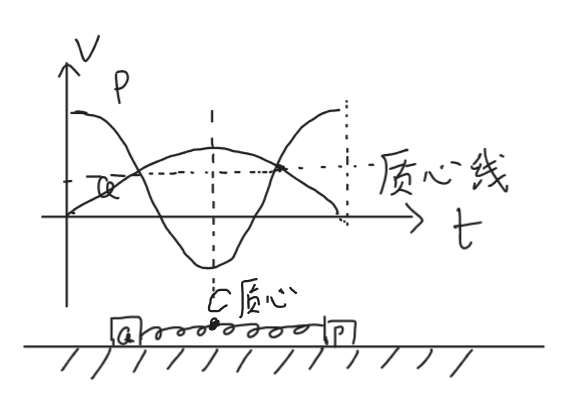
給 \(P\) 一個向左的速度 \(v_0\)，

其中 \(r,v,a\) 均為向量，有方向

\(P,Q\) 相對質心動量等大反向，整個過程中質心的速度不變

力學綜合

微量移動證明

電荷量 \(Q\)，半徑為 \(R\)，球殼表面的電荷之間將相互排斥；已知此帶電球殼體系儲存的靜電能為 \(E=k\dfrac{Q^2}{2R}\)，求球殼單位面積上受到的排斥力

運動軌跡

電場

一些基礎的公式

單電子產生的球殼電場

電場的疊加是向量，電勢的疊加是代數的疊加

例1

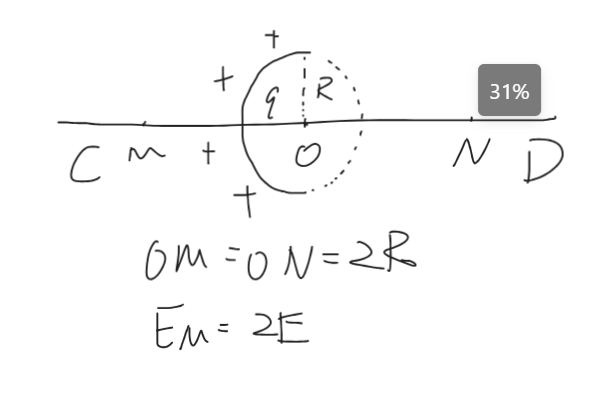
//什么情況怎么把縮放帶上了

補全法處理

1.求 \(N\) 點電場

\(E_M+E_{M'}=E_U=\dfrac{k(2q)}{OM^2}\)

\(E_N=E_{M'}=E_U-E_M=\dfrac{k(2q)}{4R^2}-2E=\dfrac{kq}{2R^2}-2E\)

2.已知 \(\varphi_M\)，求 \(\varphi_N\)

\(\varphi_M+\varphi_{M'}=\dfrac{k(2q)}{OM}=\dfrac{kq}{R}\)

周期性問題

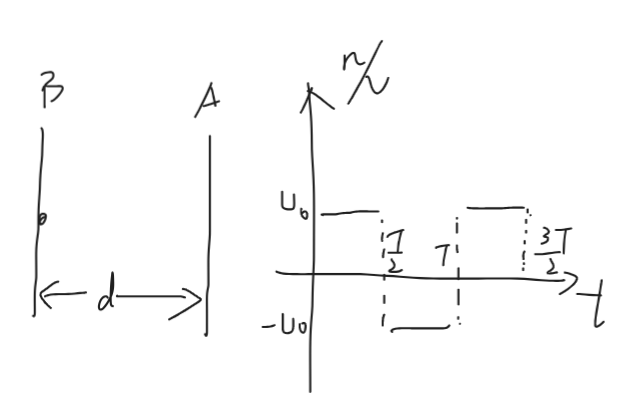
交變電壓頻率逐漸變大

等效重力場

給了一堆題自己看