CSAPP Lab1

寫了作業(yè)水一篇（記錄一下人多菜
博客園的三級(jí)標(biāo)題好小

bits.c

在bits.c中做題目
使用make clean和make進(jìn)行編譯
調(diào)用./btest -f funcName測(cè)試funcName函數(shù)的結(jié)果，可以在代碼中中插入printf輸出中間結(jié)果，但是要記得最后刪掉
調(diào)用./dlc bits.c查看是否使用了非法或過多的運(yùn)算符
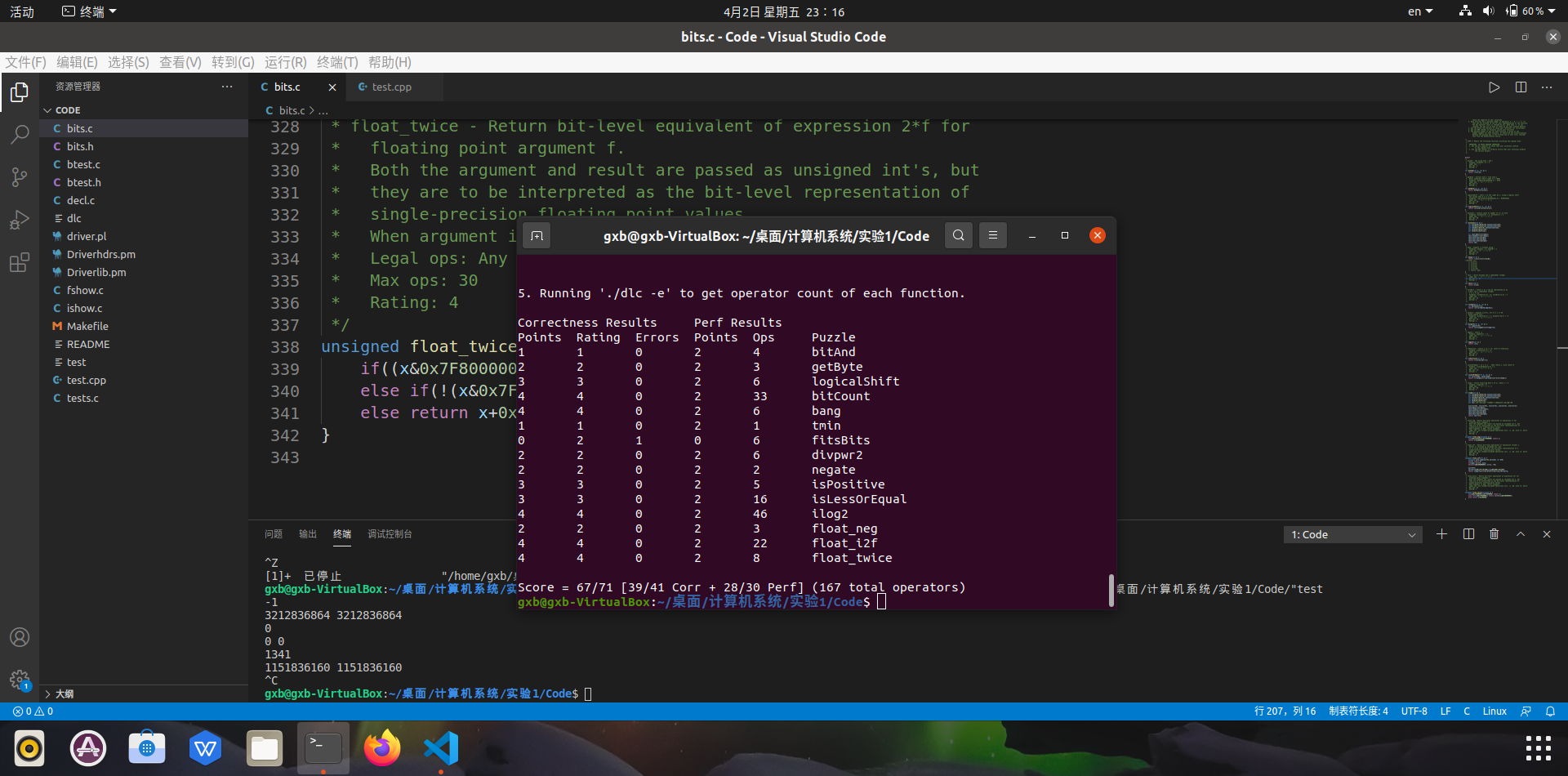
重復(fù)以上步驟，最后可以直接運(yùn)行./btest輸出最后結(jié)果。

得分圖

本地的fitsBits的Check可能有問題，沒法過。

補(bǔ)充一個(gè)位運(yùn)算優(yōu)先級(jí)圖。

bitAnd

x&y using only ~ and |
~x與~y中同時(shí)為\(0\)的位即為x&y中為\(1\)的位，或起來取反即可。

int bitAnd(int x, int y) {
	return ~(~x|~y);
}

getByte

Extract byte n from word x
用0xFF分別與x,x>>8,x>>16,x>>24即可。

int getByte(int x, int n) {
	return 0xFF&(x>>(n<<3));
}

logicalShift

shift x to the right by n, using a logical shift
簡(jiǎn)單的想法是x>>n與一個(gè)高\(n\)位為\(0\)其余全\(1\)的數(shù)\(x\)，\(x\)取反就是\(\begin{matrix}\underbrace{111}..000\\n個(gè)1\ \ \ \ \ \ \ \ \ \end{matrix}\)，用\(1<<31\)就可以算術(shù)右移\(n\)位得到高\(n\)位的\(1\)，然后再左移\(1\)位即可。

令一個(gè)想法是，\(111...000\)就是\(0xFFFFFFFF\)左移\(32-n\)位。
有三個(gè)問題及前兩個(gè)的解決方法依次是：

1. \(n=0\)時(shí)\(位移量=w=32\)，先左移\(31\)位再右移\(n\)位，最后再左移\(1\)位，避免最高位的\(1\)丟失。
2. \(0xFFFFFFFF\)右移時(shí)是邏輯右移，要轉(zhuǎn)成int或?qū)懗?span id="w0obha2h00" class="math inline">\(-1\)才是算術(shù)右移，才不丟失最高位的\(1\)，但是不能有 類型轉(zhuǎn)換 和 負(fù)號(hào)及十進(jìn)制數(shù)。
   所以必須是恰好左移\(32-n\)位，解決方法是對(duì)\(31-n\)二進(jìn)制拆分（\(31-n\)的二進(jìn)制表示比\(32-n\)更容易知道），寫成\(\log n\)個(gè)與和右移，最后再左移\(1\)位。這樣改完后代碼：(x>>n)&~(0xFFFFFFFF<<(!(n&16)<<4)<<(!(n&8)<<3)<<(!(n&4)<<2)<<(!(n&2)<<1)<<(!(n&1))<<1);。
3. 常數(shù)只能是\(0x0\sim 0xFF\)（不過可以構(gòu)造出來），以及運(yùn)算符數(shù)超過了\(20\)。所以這個(gè)方法不行。

int logicalShift(int x, int n) {
	return (x>>n)&~(1<<31>>n<<1);
}

bitCount

returns count of number of 1s in word
做法是整體的分治。令\(v_1=01\ 01\ 01\ 01...,v_2=0011\ 0011...,v_3=0000\ 1111...\)直到\(v_5=0000\ 0000\ 0000\ 0000\ 1111\ 1111\ 1111\ 1111\)。
先計(jì)算每?jī)晌恢?span id="w0obha2h00" class="math inline">\(1\)的個(gè)數(shù)\(n_2\)，即為\(n_2=(x\&v_1)+(x>>1\&v_1)\)，每?jī)晌坏?span id="w0obha2h00" class="math inline">\(1\)的個(gè)數(shù)會(huì)存在這兩位中。
再計(jì)算每四位中\(1\)的個(gè)數(shù)，即\(n_4=(n_2\&v_2)+(n_2>>2\&v_2)\)，每四位的\(1\)的個(gè)數(shù)會(huì)存在這四位中。
同理，每八位中的\(1\)為\(n_8=(n_4\&v_3)+(n_4>>4\&v_3)\)，十六位為\(n_{16}=(n_8\&v_4)+(n_8>>8\&v_4)\)，三十二位為\(n_{32}=(n_{16}\&v_5)+(n_{16}>>16\&v_5)\)，即為答案。

有個(gè)細(xì)節(jié)是，計(jì)算\(n_8\)時(shí)\(n_4+(n_4>>4)\)得到的每八位\(1\)的個(gè)數(shù)不會(huì)超過\(2^4=16\)，即不會(huì)溢出\(v_3\)中限制的\(4\)位，所以可以先加起來再一起\(\&\)減少一次操作數(shù)。\(n_{16},n_{32}\)同理。

還有限制常數(shù)最多為八位，所以需先構(gòu)造\(v_1'=01010101|(01010101<<8)=0x55|(0x55<<8),v_1=v_1'|(v_1'<<16)\)，以及\(v_2'=00110011|(00110011<<8)=0x33|(0x33<<8),v_2=v_2'|(v_2'<<16)\)，以及\(v_3'=0xF|(0xF<<8),v_3=v_3'|(v_3'<<16)\)。

int bitCount(int x) {
	int tv1=0x55|(0x55<<8),v1=tv1|(tv1<<16);
	int tv2=0x33|(0x33<<8),v2=tv2|(tv2<<16);
	int tv3=0xF|(0xF<<8),v3=tv3|(tv3<<16);
	int v4=0xFF|(0xFF<<16);
	int v5=0xFF|(0xFF<<8);

	int res=(x&v1)+(x>>1&v1);
	res=(res&v2)+(res>>2&v2);
	res=(res+(res>>4))&v3;
	res=(res+(res>>8))&v4;
	res=(res+(res>>16))&v5;
	return res;
}

bang

Compute !x without using !
結(jié)果為\(1\)當(dāng)且僅當(dāng)x=0，所以問題在于怎么將一個(gè)數(shù)的\(1\)放到個(gè)位上。有個(gè)位的\(1\)后，取反與\(1\)就可以了。

類似bitCount的分治，用x|=x>>1求出兩兩分組后的兩位中是否有\(1\)并放到低位上，然后x|=x>>2，求出四個(gè)一組的數(shù)中是否有\(1\)并放到低位上...直到x|=x>>16。

從x|=x>>16開始也可，先將\(1\)匯聚到低\(16\)位上，再x|=x>>8可以將\(1\)匯聚到低\(8\)位上，...直到x|=x>>1。

還有種方法是，利用\(0\)和\(-0\)（~x+1）的符號(hào)位均為\(0\)，而其他數(shù)中有一個(gè)\(1\)的性質(zhì)，取出這個(gè)\(0\)。即：~((x|(~x+1))>>31)&1。

int bang(int x) {
	return ~((x|(~x+1))>>31)&1;
//Another sol:
	// x|=x>>1;
	// x|=x>>2;
	// x|=x>>4;
	// x|=x>>8;
	// x|=x>>16;
	// return ~x&1;
}

tmin

return minimum two's complement integer
即1<<31。

int tmin(void) {
	return 1<<31;
}

fitsBits

return 1 if x can be represented as an n-bit, two's complement integer.
若\(-2^n\leq x\lt 2^n\)，則\(x\)若為正數(shù)，則高\(32-n\)位均為\(0\)，若為負(fù)數(shù)，則高\(32-n\)位均為\(1\)。所以\(x\)左移\(32-n\)位后再右移\(32-n\)位應(yīng)不變。否則\(x\)越界則\(x\)數(shù)值會(huì)改變。
注意32-n=32+(~n+1)，a==b可以改寫為!(a^b)。

int fitsBits(int x, int n) {
	int delta=33+(~n);
	return !(x^(x<<delta>>delta));
}

divpwr2

Compute x/(2^n), for 0 <= n <= 30 (Round toward zero)
\(x\)為正數(shù)則為\(x>>n\)，為負(fù)數(shù)則為\(x+(1<<n)-1>>n\)。
將\(1\)替換成\(x\)的符號(hào)位即可。注意若\(x\)為負(fù)則\(x>>31=-1\)，提取符號(hào)位需要\(\&1\)，但可以直接作為減\(1\)。

int divpwr2(int x, int n) {
	int sign=x>>31;
	return (x+((sign&1)<<n)+sign)>>n;
}

negate

return -x
~x+1。

int negate(int x) {
	return ~x+1;
}

isPositive

return 1 if x > 0, return 0 otherwise
需要判\(0\)，而\(-0\)的符號(hào)位不變，所以同divpwr2中用\((-x>>31)\&1\)提取\(-x\)的符號(hào)位即可。但有個(gè)問題是\(-TMIN=TMIN\)，所以還要特判\(TMIN\)否則不對(duì)。
更簡(jiǎn)單的是直接求符號(hào)位，然后\(\&(!!x)\)來特判\(0\)。

int isPositive(int x) {
	return (!(x>>31))&(!!x);
}

isLessOrEqual

if x <= y then return 1, else return 0
如果不溢出就是isPositiveOrZero(y-x)即!((y-x)>>31&1)。注意到y-x溢出只發(fā)生在\(x,y\)異號(hào)，而異號(hào)可以直接判斷大小。所以先求一下\(x,y\)的符號(hào)位判斷是否溢出即可。

int isLessOrEqual(int x, int y) {
	int sx=x>>31&1, sy=y>>31&1;
	return ((!sy)&sx)|(!(sy^sx)&!((y+~x+1)>>31&1));
}

ilog2

return floor(log base 2 of x), where x > 0
即求最高位的\(1\)。最簡(jiǎn)單的方法是再最高位右邊全填上\(1\)，再用bitCount-1。
填充\(1\)類似bang，x|=x>>16,x|=x>>8,...,x|=x>>1，從高位傳下來即可。也同bang先x|=x>>1最后x|=x>>16都可。

還有種方法是，先求出高\(16\)位是否有\(1\)，有就加\(2^{16}\)；然后再求當(dāng)前\(16\)位中高\(8\)位是否有\(1\)，有就加\(2^8\)...直到最后一位。

int ilog2(int x) {
	int tv1=0x55|(0x55<<8),v1=tv1|(tv1<<16);
	int tv2=0x33|(0x33<<8),v2=tv2|(tv2<<16);
	int tv3=0xF|(0xF<<8),v3=tv3|(tv3<<16);
	int v4=0xFF|(0xFF<<16);
	int v5=0xFF|(0xFF<<8);
	int res;//鍙よ€佺殑csapp鏍囧噯瑕佹眰C涓嚱鏁板０鏄庡繀欏昏鍦ㄦ渶鍓嶉潰

	x=x|(x>>16), x=x|(x>>8), x=x|(x>>4), x=x|(x>>2), x=x|(x>>1);
	res=(x&v1)+(x>>1&v1);
	res=(res&v2)+(res>>2&v2);
	res=(res+(res>>4))&v3;
	res=(res+(res>>8))&v4;
	res=(res+(res>>16))&v5;
	return res+~1+1;
}

float_neg

Return bit-level equivalent of expression -f for floating point argument f.
實(shí)數(shù)取反，取反符號(hào)位即可。要特判NaN。

unsigned float_neg(unsigned x) {
	if((x&0x7FFFFFFF)>0x7F800000) return x;
	return x^0x80000000;
}

float_i2f

Return bit-level equivalent of expression (float) x
若\(x\)為負(fù)數(shù)，則先將\(x\)取反；為\(0\)可直接特判。
設(shè)最高位的\(1\)為第\(i\)位，則浮點(diǎn)數(shù)的階碼\(E\)為\(i+Bias=i+127\)，小數(shù)子段\(f\)則為低\(i\)位（如果小于\(23\)位則后面補(bǔ)\(0\)，大于\(23\)位則舍棄并進(jìn)位，注意是向偶數(shù)舍入！）。最后再加上符號(hào)位。
具體：
用前面方法或循環(huán)找到最高位的\(1\)，設(shè)其距第\(31\)位距離為\(d\)，則直接將ux=(unsigned)x左移\(d+1\)位，使小數(shù)子段確定為\(ux\)的\(31\sim 9\)位，舍棄位為\(8\sim 0\)位。
偶數(shù)舍入兩種情況：1. 舍棄的\(9\)位大于\(2^9\)，即ux&0x1FF>0x100；
2. 有效位和最高舍棄位均為\(1\)，即第\(9\)位和第\(8\)位均為\(1\)，即ux&0x300==0x300或ux&0x3FF>=0x300。（我怎么總是忘了位是從\(0\)開始標(biāo)號(hào)）

最高符號(hào)位，加上從\(23\)位開始的\(低位個(gè)數(shù)+127\)，最后加上小數(shù)子段\(ux>>9\)和進(jìn)位即為答案。

unsigned float_i2f(int x) {
	unsigned ux=x,sign=ux>>31,carry=0; int d=0;
	if(!x) return 0;
	if(sign) x=~x+1, ux=x;
	while(!(x&0x80000000)) x<<=1, ++d;

	ux<<=d+1;
	carry=((ux&0x1FF)>0x100)|((ux&0x300)==0x300);
	return (sign<<31)+((31-d+127)<<23)+(ux>>9)+carry;
}

float_twice

Return bit-level equivalent of expression 2*f for floating point argument f.
如果是規(guī)格化數(shù)，直接階碼\(+1\)（直接加0x800000）；
如果是非規(guī)格化數(shù)，只需將\(x\)左移\(1\)位（注意符號(hào)位）。
特殊值則直接返回。

unsigned float_twice(unsigned x) {
	if((x&0x7F800000)==0x7F800000) return x;
	else if(!(x&0x7F800000)) return (x<<1)|(x&0x80000000);
	else return x+0x800000;
}

其它

找出一個(gè)數(shù)中的第\(k\)個(gè)1
https://stackoverflow.com/questions/7669057/find-nth-set-bit-in-an-int