圖論基礎
Table of Contents
前言:
眾所周知,圖論,是算法與數據結構高度統一的一部分,也是一塊硬骨頭;
但是,我們這些學計算機的人,不就是應該迎難而上嗎;
所以,在開學前的最后4天,本蒟蒻準備開始啃圖論了;
讀完本文,你將對圖和圖的基礎概念有一個深刻的認知;
前置知識:無(不過,如果你已經知道‘集合’和‘二元關系’這兩個詞,閱讀體驗會更絲滑)
什么是圖:
我們先講講為什么會有圖
想象一下,現在有一個巨大的社交網絡,其中每個人都與若干個人有聯系
如果是你,你會怎么表示它的數學模型呢(或者說,你會怎樣把它抽象出來,使它易于表示、觀看);
一個很顯然的做法是:將人抽象成點,將人與人的關系抽象成線,兩個點有連線,當且僅當這兩個點代表的兩個人有聯系;
也就是說,兩個人有聯系時,我們就把他們連起來;
那么,恭喜你,發明了圖!
圖就是將復雜的關系簡單化的一種數據結構,能夠輕而易舉地看出復雜關系,并加以研究;
比如如下兩個圖:
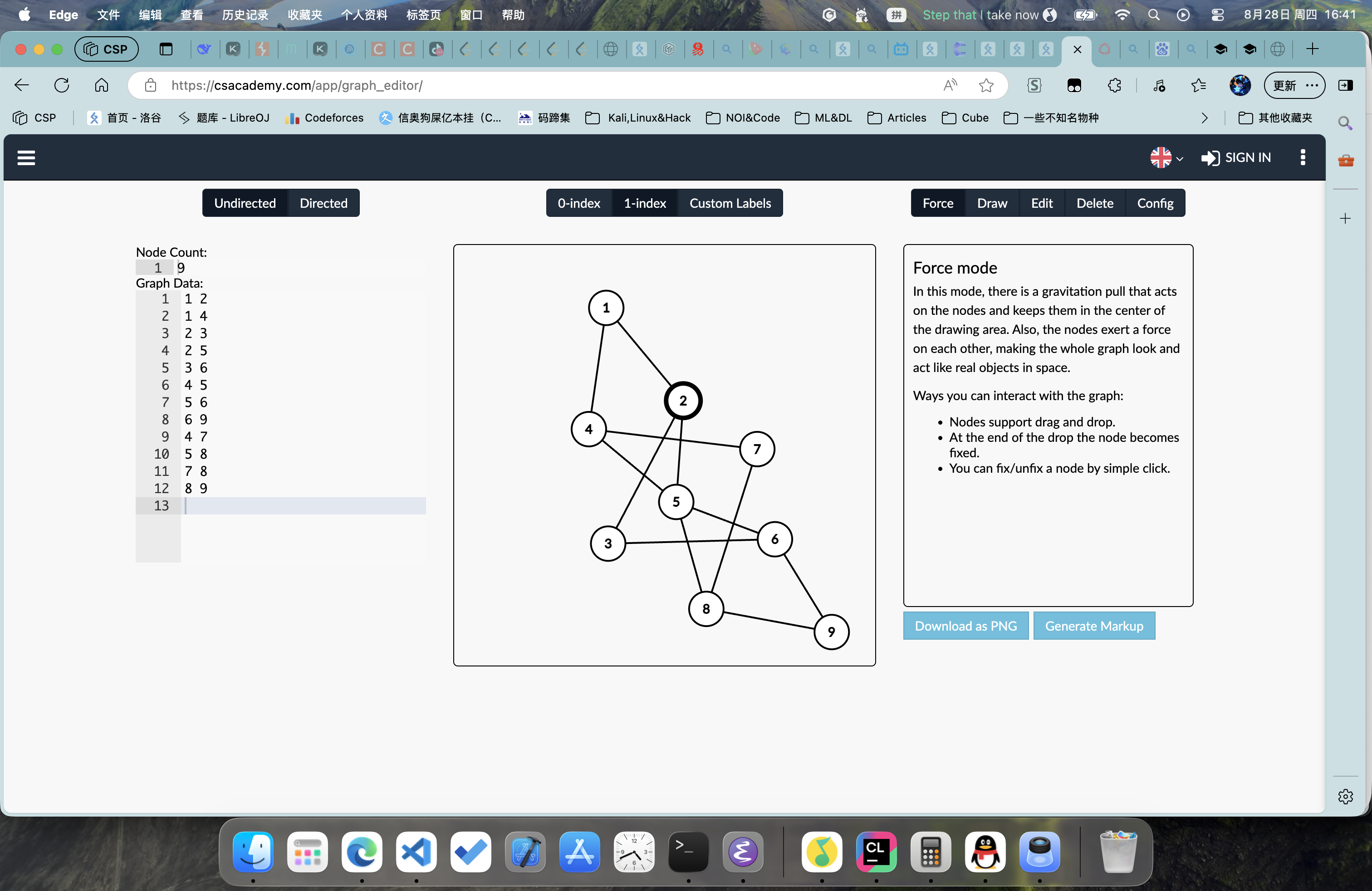
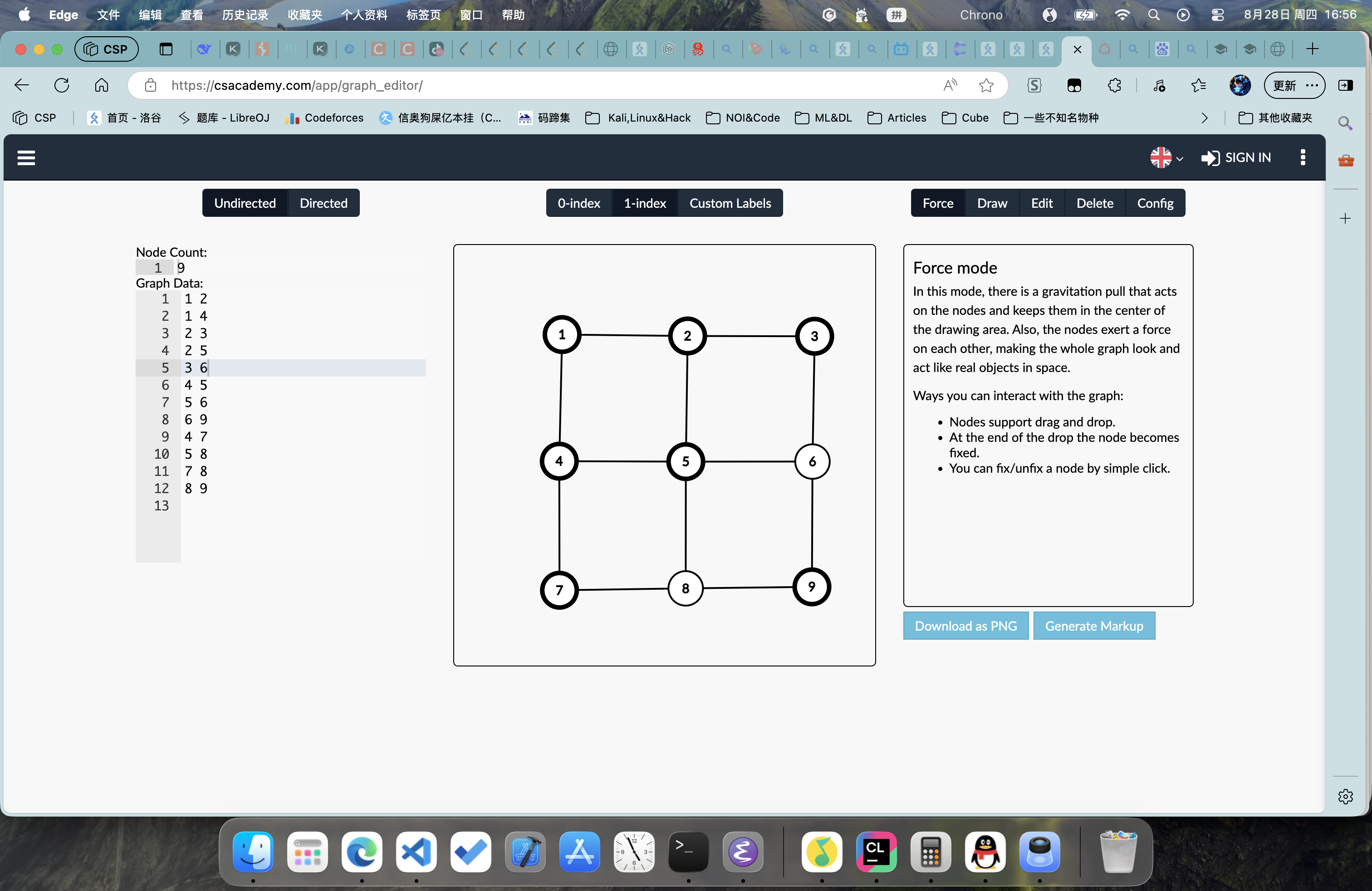
僅看第一張圖,你完全不知道這是什么;
現在我告訴你,它和第二張是等價的;
相信,通過這個例子,你能夠知道圖的力量了;
圖還有一個非常著名的應用:地圖軟件(當然,這都老生常談了),我們將任何一個位置抽象成點,兩點之間的線的長度就是兩點之間的距離,隨后找出起點和終點的最短路即可;
通過這兩個例子,不難發現,每張圖都有點、邊這兩個東西,因此,圖的定義是這樣的:
**給定兩個集合: \(V、E\) ,其中 \(V\) 存放所有的點, \(E\) 存放所有的邊,圖 \(G\) 就是這兩個集合的組合:\(G = (V,E)\) ;
**
我們依次解釋里面的幾個地方:
由于 \(V\) 存放所有的點,我們稱 \(V\) 為點集,這與高中數學中常見的點集是一樣的;
由于 \(E\) 存放所有的邊,我們稱 \(E\) 為邊集;
怎么表示一個邊呢?若有兩個點 \(u,v\) , \(u,v\) 之間的邊用**無序的對** \({u,v}\) 表示,所以, \(E\) 大概是這樣的: \(E = \{\{u_1,v_1\},\{u_2,v_2\},\cdots \{u_n,v_n\}\}\) ;
顯然,其中的每個點必須是 \(V\) 中的一個點,否則就是沒有意義的;
一些補充:點,有的地方也叫做頂點、節點;
圖的基礎概念:
不要一聽到基礎概念就跑路,僅僅去羅列概念是沒有用的,看完就會忘;學算法更重要的是理解本質;
Part 1.有向圖、無向圖、加權圖
那么仍然是根據地圖和社交網絡的例子:
小A認識小B代表小B認識小A嗎,顯然不是;
一條路是否可以是單行道呢,顯然可以;
到目前為止,我們把邊畫成了“沒有箭頭”的線段
——這意味著“張三認識李四”與“李四認識張三”被當成同一件事
那么怎樣表示小A認識小B,而小B不認識小A呢? 我們可以畫一個小A指向小B的箭頭,這樣就代表示小A認識小B,小B什么也不做(沒有指向小A的箭頭),這就表示,小B不認識小A;
再比如在地圖中,若是AB兩點只允許A通向B,我們就將A指向B,這代表從A到B有路;
所以對于某些情況,邊是有指向性的,我們把這樣的圖叫做有向圖;
相應的,邊沒有指向性的圖就叫做無向圖;
那么無向圖和有向圖有什么區別呢?
注意到:在定義中,我提到了:邊使用無序的對表示,這表明了,由 \(u\) 向 \(v\) 連接還是由 \(v\) 向 \(u\) 連接都無所謂,是一樣的;
但在有向圖中,這并不等價,我們需要定義邊究竟是誰指向誰,所以,這里需要使用有序對,我們使用小括號,記為 \((u,v)\) ,代表有一條從 \(u\) 指向 \(v\) 的邊;
也就是說,之前的定義是無向圖的定義,而修改為有序對之后就是有向圖的定義;
到目前為止,這張地圖、社交網絡完整了嗎?
顯然,沒有,地圖需要比例尺來確定兩點間的距離,社交網絡也需要一個值衡量兩個人的好感度,這就意味著,我們的邊需要一個長度,它代表著,兩點的距離、兩個人的好感度;
我們把這種邊長有值的圖叫做賦權圖、加權圖,權,就是這條邊的長度,如圖:
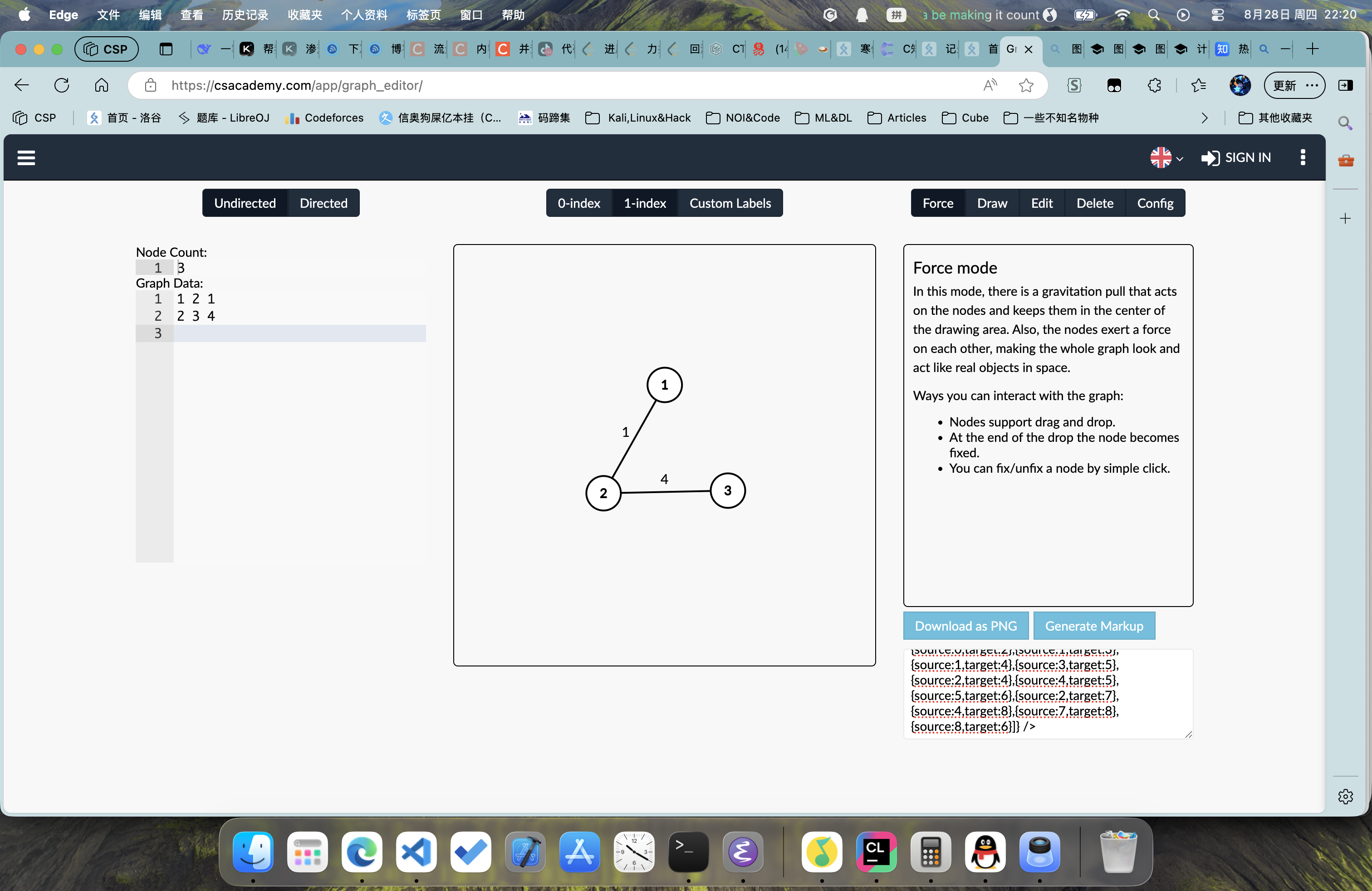
這樣,我們就完成了地圖與社交網絡的表示;
Part 2.度,入度,出度,聯通圖
接下來,我們介紹另一個概念:度;
何為度呢,度就是與一個點有關系的點的數量;
換言之:就是與這個點相連的邊的數量;
特別的,在有向圖中,指向這個點(以這個點為終點)的邊的數量叫做這個點的入度;反之,從這個點出發的邊的數量就是這個點的出度;
也就是說,只有有向圖分入度、出度,無向圖只有度;
我們稱無向圖中度數為偶數的點為 偶點,度數為奇數的點為奇點;
再引入一個問題,就是著名的一筆畫問題:給你一張圖,如何能判斷這張圖是否能一筆畫完;
即:從某點出發,經過每條邊**恰好**一次,最后停在一個點;
歐拉給出了一筆畫定理:當且僅當一個圖聯通,并且這張圖上奇點個數為0或2時可以一筆畫成;
這是為什么呢?
- 首先,什么是連通:故名思義,就是從一點出發,可以沿著邊到達一些點后繼續沿著邊前進,能夠達到所有的點,換言之,就是沒有任何一個孤立的點,我們稱這張圖連通;
- 隨后,為什么奇點個數為0時可以一筆畫:
想象一下,你正在一筆畫一個圖形。每當你用筆經過一個頂點時,必定是“一進一出”
假設你從起點A出發。每當你的路徑進入一個頂點(比如B),就必須有一條“尚未使用”的邊讓你離開B(除非B是終點)。這個“進入”和“離開”的動作,會消耗掉與頂點B相連的兩條邊。
因此,對于路徑上的中間頂點(不是起點和終點的點),與之相連的邊必須成對出現,即它的度數必須是偶數
那么起點和終點呢?
如果你的路徑最終要回到起點(形成回路),那么起點在最初“離開”了一次,最終又“進入”了一次。這一出一進同樣消耗了兩條邊。所以,起點/終點也必須是偶度數。
因此,存在歐拉回路(一筆畫的時候起點就是終點)的圖,所有頂點都必須是偶度數;
- 為什么奇點個數為2可以一筆畫:
現在,假設你的路徑不需要回到起點。那么,起點和終點將是兩個不同的頂點。
起點:你從這里出發,只“離開”不“進入”。因此,與起點相連的邊被消耗掉的次數是奇數(第一次離開,之后可能進出多次,但總次數為奇)。
終點:你最終到達這里,只“進入”不“離開”。因此,與終點相連的邊被消耗掉的次數也是奇數。
中間頂點:依然是“一進一出”,消耗偶數條邊。
所以,在這種情況下,整個圖有且只能有兩個頂點擁有奇數度數,它們分別就是路徑的起點和終點
證畢.
相信通過這個例子,你能夠深刻地理解圖論的一些基礎概念;
一些補充:聯通,也寫做「連通」,大部分資料都是使用「連通」;
圖的存儲:
Part 1.鄰接表存儲
接下來我們講如何把一張圖存在計算機中,如果是你,你會怎么辦呢?
大部分人的想法是:遵循圖的定義,使用一個集合存點,另一個集合存邊,但是,這么做的代價是:每次從一個點到另一個點,需要查看所有的邊才行(這樣才能找到與這個點相連的邊);
那么怎么優化一下呢?
我們可以給每個點都開一個集合,里面存放與這個點相連的邊;
更進一步,對于無向圖,由于這里面的邊都與這個點相連,我們可以只存另一個點,優化內存;對于有向圖,這個點的集合存放的就是以這個點為起點的邊,同樣,由于都是以這個點為起點,我們也可以只存另一個點;
那么,恭喜你,發明了圖的鄰接表存儲;
鄰接表存儲:給每個點都開一個數組,數組的成員即為與這個點相連的點的編號,若圖有權,再另開一個權數組,對應存權值;
鄰接表的鄰接,就是「這條邊與這個點相鄰、相接」的意思;
補充:由于需要兼容有向圖,并且更好地操作,如果是無向圖,我們需要在u的集合存v,在v的集合存u;
Part 2.鄰接矩陣存儲
眾所周知,沒有絕對完美的結構,每種方式總有缺點,如果沒有,那么這種結構一定非常復雜;
那么鄰接表又有什么缺點呢?
我們先想想對于圖,會有什么操作:最簡單的,就是查詢 \(u,v\) 間是否有邊;
鄰接表的查找,很顯然,需要遍歷u的集合的所有成員,也就是 \(O(n)\) ,更準確地講,這跟u的度有關,我們把一個點u的度記為 \(d(u)\) ,那么時間復雜度是 \(O(d(u))\) ;
有一種做法,可以將「查詢 \(u,v\) 間是否有邊」的時間復雜度降低至 \(O(1)\) ,而根據我們的經驗,這一定是要付出一些代價的;
這次的代價是:空間;
我們以空間換時間,定義一個矩陣 \(G\) , \(G_{i,j} = 1\) 代表有一條從i到j的邊(仍然是為了兼容有向圖),若是這是加權圖,我們將1改為權即可;
這種方法簡單、粗暴,弊端也很明顯:當一個圖點數很多,而邊很少的時候,會浪費大量的空間;
但這正是鄰接表的優點;
我們做一個總結:在稀疏圖(即點多、邊少)中,我們使用鄰接表,在稠密圖中,我們使用鄰接矩陣;
結語:
“人生如棋,我愿做卒”
“行動雖緩,可誰曾見我后退一步!”
這篇文章只是對圖的一個初步認識,接下來會陸續更新圖論算法;
如有筆誤,煩請不吝賜教
Upt 2025.8.28 22:22


 浙公網安備 33010602011771號
浙公網安備 33010602011771號