一.尺度空間理論與高斯分布的概率密度函數

1.尺度空間理論

尺度空間理論目的是模擬圖像數據的多尺度特征，高斯卷積核是實現尺度變換的唯一線性核（只有高斯卷積核才能對圖像近大遠小，近清晰遠模糊的效果），于是一副二維圖像的尺度空間定義為:

(x，y)是空間坐標，σ是尺度坐標它的大小決定圖像的平滑程度，大尺度對應圖像的概貌特征，小尺度對應圖像的細節特征。大的值對應粗糙尺度(低分辨率)，反之，對應精細尺度(高分辨率)。

 

2.高斯函數的概率密度函數

一維

 方差越大，高斯分布越平緩，在高斯分布做掩膜的時候周圍像素對中心像素的影響就越大（也就是中心像素沒那么大權重了），這樣圖像就越平滑，從而圖像也越模糊，這樣細節就會丟失。

方差較小

方差較大

   多維

       

 

 

 

     

二.步驟

1.尺度空間的建立

1.1高斯金字塔的建立

 

 

 

 

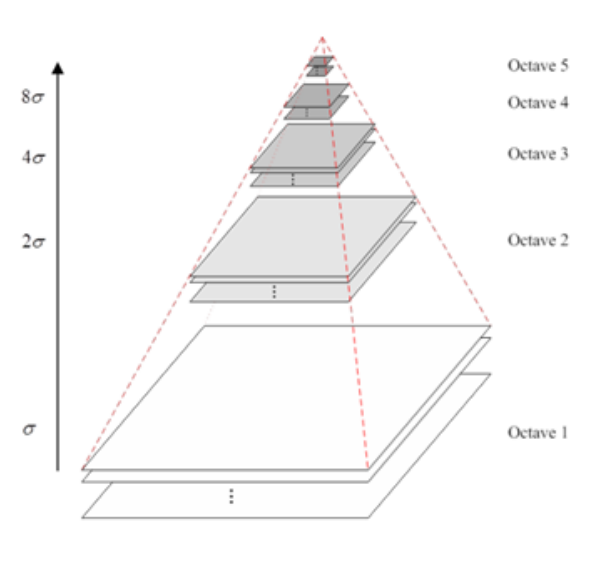
就看想要在幾層高斯差分金字塔中求極值了，層數越多越精確。往往尺寸大的圖像組數和每組中的層數要多一些。

說明：

1.每一組圖片是固定尺度的圖像進行高斯模糊得到的，組內圖片的不同之處在于高斯的方差不同（這里也叫做尺度不同）

對于圖像的高斯模糊我們的方法有：

根據3σ原則，使用NxN的模板在圖像每一個像素點處操作，其中N等于大于6σ+1的第一個奇數。

 

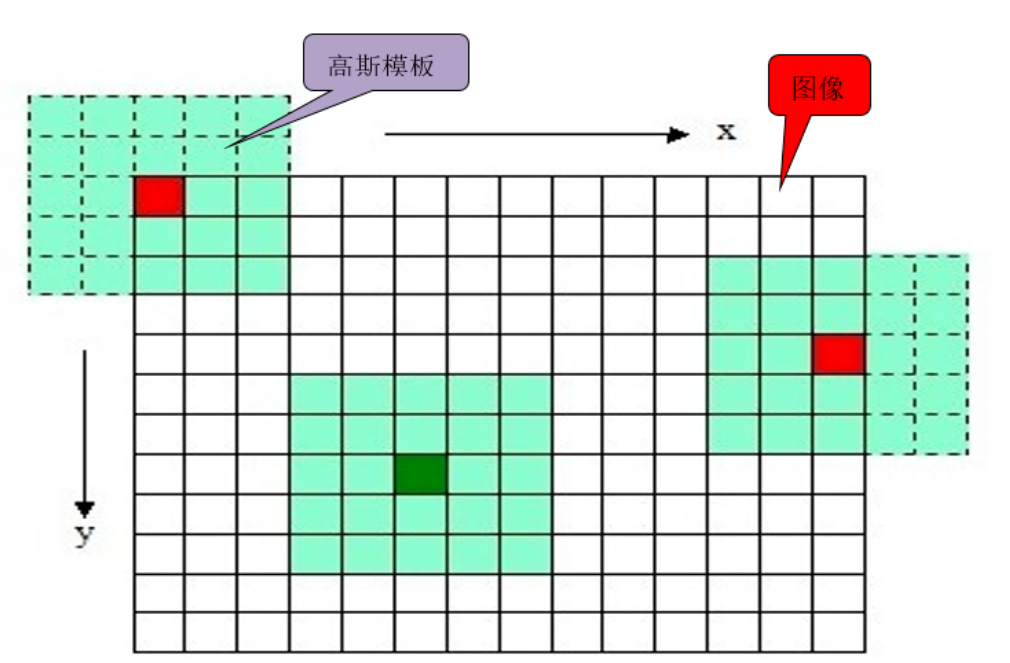
上面這樣直接與圖像卷積，速度比較慢，同時圖像邊緣信息也會損失嚴重。后來不知哪位學者發現，可以使用分離的高斯卷積（即先用1xN的模板沿著X方向對圖像卷積一次得到一個圖像，然后用Nx1的模板沿著Y方向對沿著X方向卷積得到的圖像再卷積一次，其中N還是等于大于6σ+1的第一個奇數），這樣既省時也減小了直接卷積對圖像邊緣信息的嚴重損失。

 

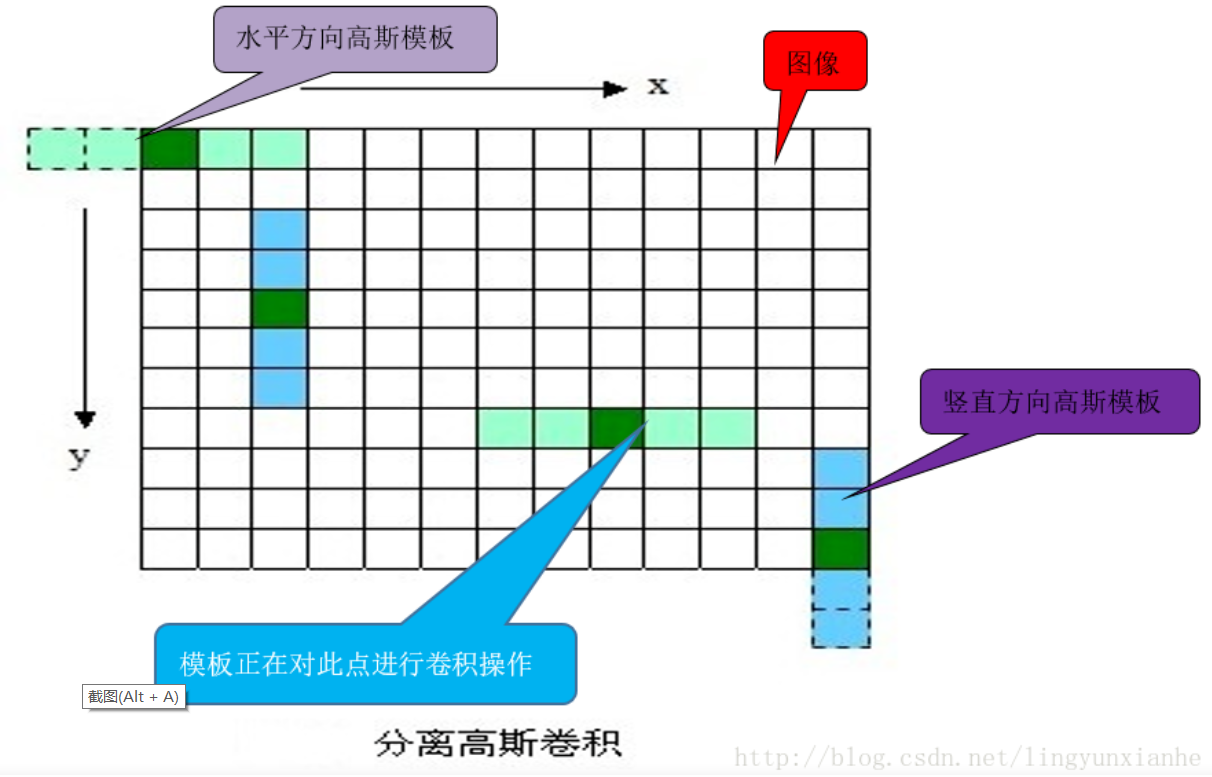
2.而不同組之間的圖像是通過對原圖片降采樣得到的（例如每隔一個像素點取一個像素點），也就是不同組之間的圖像尺寸是不同的

3.高斯卷積的好處：首先個人認為圖像模糊有兩點原因：第一圖像尺寸太小，第二圖像被平滑丟掉了許多細節信息。所以如果沒有高斯卷積直接對圖像進行降采樣，圖像就會丟失掉大部分的像素點，這樣就顯得不夠連續。而對每個尺寸的圖像進行多次不同尺度的高斯平滑（高斯平滑前后的圖像相對連續一些），這樣前一組的最后一張圖像和下一組的第一張圖像就相對連續一些，這樣整體的高斯金字塔圖像的變化就相對連續一些。

每組每層的Б的確定：

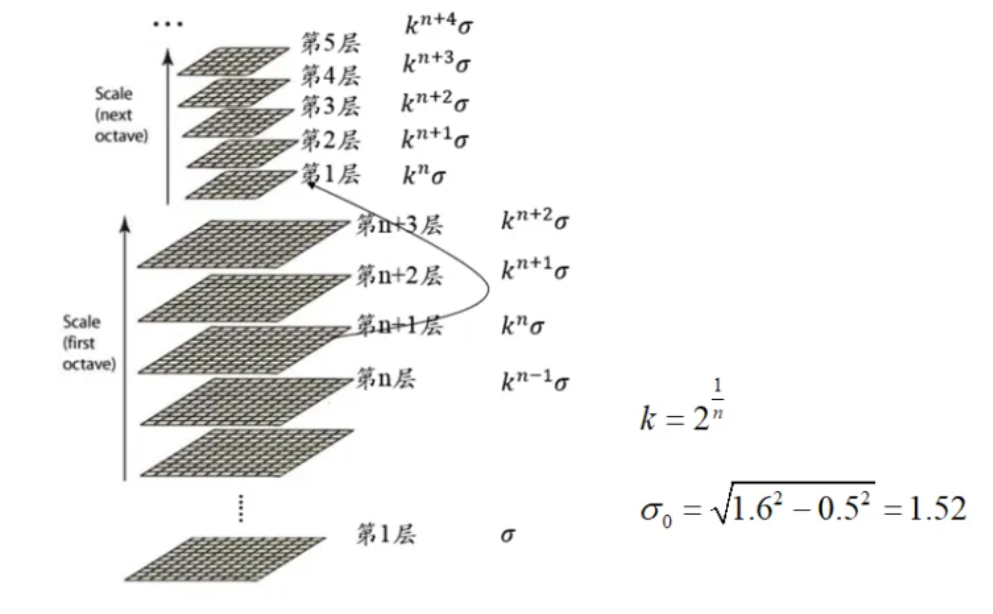
說明

1.下一組的第1層為上一組倒數第4層降采樣所得，無須進行高斯模糊操作.

2.

 對圖像進行Б=0.5的平滑，再對圖像進行Б=1.52的平滑，總體的效果可以達到Б=1.6的平滑，它們之間滿足勾股定理的關系。

1.2高斯差分金字塔的建立

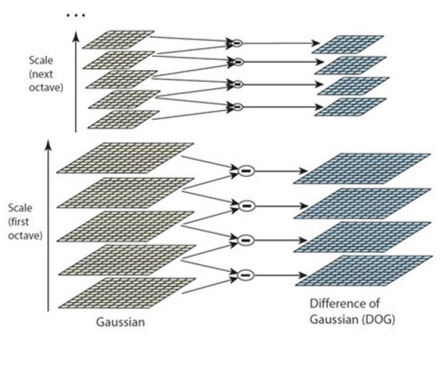
2.關鍵點的位置確定

 

2.1.閾值化

n為1.1第二張圖片左下角的n（想要在幾層中提取極值點）

 2.2.在高斯差分金字塔中找極值

 注意要舍去第一層和最后一層

2.3.尋找亞像素的極值

1.擬合曲線

當我們檢測到極值點之后，會發現一個問題，高斯差分金字塔是離散的(因為尺度空間和像素點都是離散的)，所以找到的極值點不太準確的，很大可能在真正極值點附近(達到亞像素精度)，同時去除低對比度的關鍵點和不穩定的邊緣響應點(因為DOG算子會產生較強的邊緣響應)，以增強匹配穩定性、提高抗噪聲能力。

亞像素極值點的獲取如下：

 

 

當任一維度上的偏移量小于0.5時（即x或y或 σ），終止迭代，否則：

在Lowe論文中中進行了5次迭代終止算法。有個問題，從第二次迭代就是亞像素了，亞像素的有限差分怎么求，包括最后的亞像素函數值怎么求

  

 上面的圖片所有異界偏導和二階偏導都少一個， h一般取1

 

 

 

 

 

 

注意這里面的D是f，此步將所有的邊緣點給去掉了

至此就在高斯差分金字塔中找到了亞像素的極值點（x,y,Б‘）也就是關鍵點，這個極值點可能不在任何差分金字塔的平面。

3.關鍵點賦予方向

上面的高斯金字塔已經保證了特征點的尺度不變性

3.1.主方向的選取

上一步中我們已經求得差分金字塔中關鍵點的位置（x,y,Б‘），那么高斯金字塔中的關鍵點的位置也就是（x,y,Б‘‘）其中Б‘‘是最接近Б‘的（在高斯金字塔中找到一層，該層的Б與Б’最相近）注意此時的關鍵點個人定義為層內關鍵點（當然一組中肯定有好多個關鍵點，這里以一個關鍵點為例）。這里為什么不在高斯金字塔上找關鍵點解釋如下：

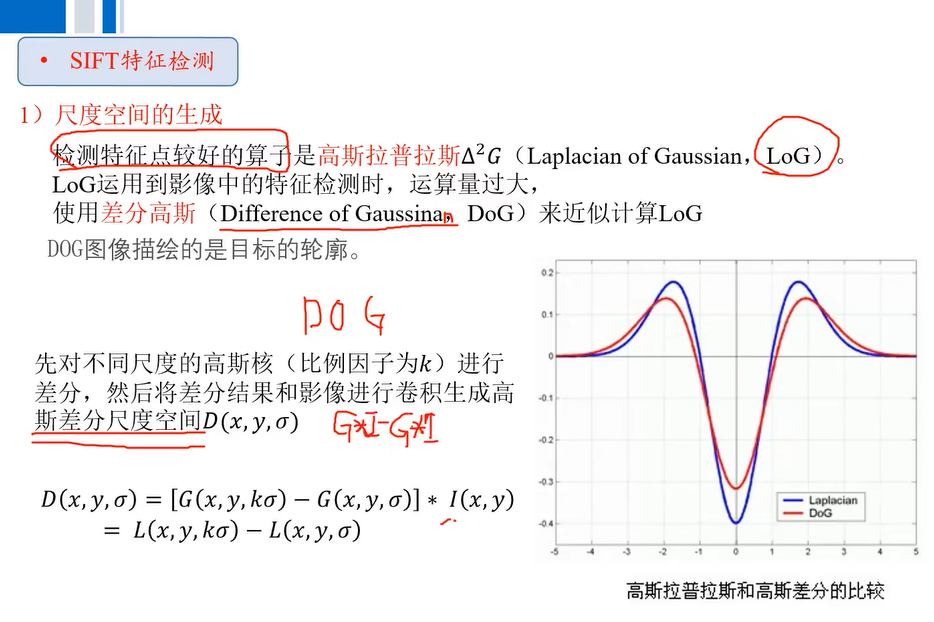
以該關鍵點為圓心1.5Б‘為半徑畫個圓我們統計它們的梯度方向和梯度幅值，然后用高斯濾波對這些像素濾波，用來統計的直方圖的y軸是濾波后的幅值累加，x軸的確定原則如下：

以10柱為例0~36是一個區間，37~72是一個區間....以此類推。而每個像素求過梯度方向后就可以判斷它在哪個區間了（所有在0~36區間中的像素的梯度方向統一認為是36度）

如果一個像素在0~36的區間內，則橫坐標為36度的那個點的幅值就加上該像素的濾波后的幅值。

 

最后柱形圖中最高點為主方向，同樣如果其他主體的高度有大于等于主方向80%，那么就稱這個方向為輔方向，那么一個關鍵點就變成了兩個關鍵點，它們同樣位置同樣尺度不同方向。

 

3.2描述符的確定

這里說一下旋轉不變性，如果水平建立x軸，豎直建立y軸，這樣就是旋轉改變了，如果一個像素的梯度方向是45度，那么圖像旋轉一個角度后，如果還以水平為x軸，豎直為y軸，那么這個像素的梯度方向就不再是45度。如果我們將所有像素的梯度方向變成一相對梯度方向，那么就會具有旋轉不變性，怎么找呢，就是將將所有像素的梯度方向中選一個梯度方向作為x軸，與之垂直的就是y軸，該梯度方向就是主方向，這樣你無論怎么旋轉圖像，每個像素的相對梯度方向就永遠不會變，這就是旋轉不變性。

在關鍵點周圍找一個正方形區域（邊長為,m=3,d=4（論文中所取）Б為關鍵點的Б），首先將該區域旋轉到主方向，也就是將主方向作為x軸（從這里也可以看出來主方向和輔方向的特征描述子也不盡相同），方便計算嘛。然后將該區域分解為4*4個子區域。然后將每個子區域還像3.1那樣根據每個子區域的所有像素求解每個子區域中36度所對應的幅度，72度所對應的幅度......

 

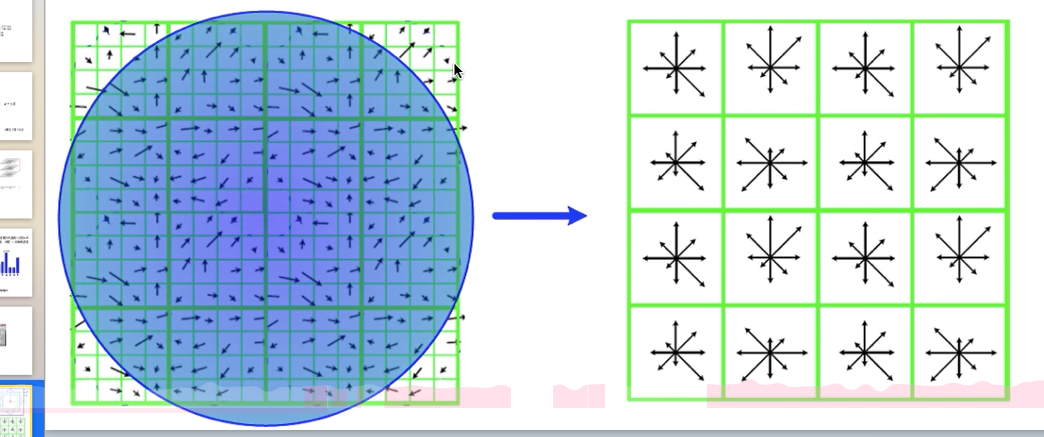
這樣每個子區域有8個方向，一個方向的幅度為一個特征向量，一共有16個子區域，也就是有128個特征向量。

 

 感覺和Census變換一樣，求解的是一個相對的特征向量，當受到不同光照后，特征向量的所有值一起變，所以歸一化后的值不變。

 3.3整個圖像的關鍵點以及它的描述子的獲取

將某一層的關鍵點（x,y,Б)映射到原圖像上，該關鍵點的位置為（x^組數-1，y^組數-1),描述子不變，注意這已經是亞像素位置了

4.圖像的匹配

將左圖像的一個關鍵點和所有的右圖像的關鍵點的描述子求歐式距離歐式距離最小的則為匹配點，或則用Kd樹？這個我還沒學后續要補上

注意：尺度不變，光照不變，旋轉不變的意思是，圖像和它尺度縮放，旋轉，加光照，后的圖像仍然能匹配得上

 

 

以上是個人一些見解，標綠的地方是不確定的地方，歡迎大家批評指正，隨筆有些圖是在網上上截取的，侵權刪除。

感覺這個算法就是個無底洞，每次看都有新的問題，所以今后打算看看原論文，或則多讀讀代碼。

參考文章：

1.SIFT算法 - 知乎 (zhihu.com)

2.https://www.bilibili.com/video/BV1Qb411W7cK/?p=3&spm_id_from=0.0.header_right.history_list.click

3.4.2 點特征提取-SIFT_嗶哩嗶哩_bilibili

4.https://blog.csdn.net/lingyunxianhe/article/details/79063547

5.SIFT 特征提取算法總結 - 飛奪瀘定橋 - 博客園 (cnblogs.com)