基本技巧

• 01 串轉化為走網格圖。如果是 \(1\) 向右，\(0\) 向上的話，順序對數就是面積大小。

• 括號序列轉折線圖。可以和反射容斥結合。

• 區間包含/不交關系：樹。括號串也可以看成一堆區間。

• 走若干步回到自己，考慮置換環相關。\(i\to a_i\) 構建基環樹。

• 逆序對和偏序信息可以放到二維平面處理。

P9338 [JOISC 2023] Chorus (Day3)

轉化為折線圖，\(A\) 向右上走，\(B\) 向右下走。最嚴格條件是 \(k\) 個連續單峰函數，每個峰端點高度均為 \(0\)，也就是底座在坐標軸上。

由于不是連續選擇元素，而是可以選擇子序列，所以只要當前折線畫出來之后輪廓包含住了上述最嚴格折線必然合法，這個條件是充要的。如圖 \(k=5\) 的時候，黑色曲線就是其中一個最嚴格折線，而紅色折線這個時候包含住了黑色折線，因為它也是合法的。

考慮何時能夠包含住最嚴格曲線，對于當前序列的曲線畫出來之后，我們能在當前曲線下方任意行走。由于我們可以 ABAB 這樣子快速上下來構造峰，所以峰的個數很容易多，只要我們能走出 \(\le k\) 個峰就一定能走出 \(k\) 個峰（總長一定的情況下，把大峰拆成若干小峰就可以增加個數），所以貪心地盡可能走出盡量少的峰。

可以現在我們在目前折線下不一定能走出 \(\le k\) 個峰，所以需要將原折線進行翻折使得其去包含住一些峰。

交換相鄰 \(A,B\) 其實就是把一個谷低/峰進行翻折（本題翻折峰沒有意義）。翻折一大段的代價就是其面積，翻折面積的意義為逆序對數量。據此進行 dp。借用一張 Rainbow_qwq 博客園里面的圖，黑色的是原折線，紅色的是最嚴格折線。我之前試過很多對于黑色折線 dp 的方式，但是都失敗了，因為黑色折線波動的規律其實是不多的，我找到了一些但是都不充要，所以我們考慮對于紅色折線進行 dp，然后讓黑色折線去滿足紅色折線的要求，這樣子就不需要對于黑色折線的形態去刻畫充要條件了。

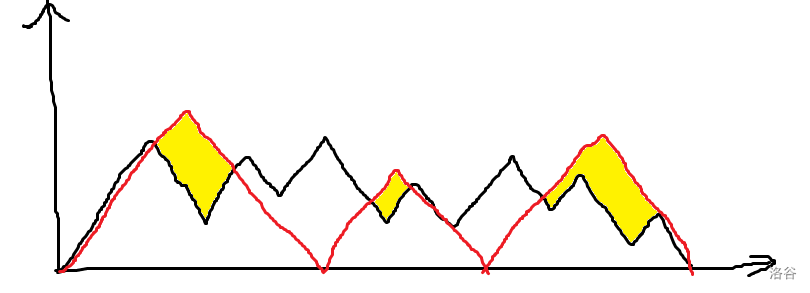
設 \(f_{i,j}\) 表示對于前 \(i\) 個位置劃分出 \(j\) 個最嚴格峰的最小代價，其中 \(i\) 表示第 \(j\) 個峰結束的位置，就是最后一個峰下降到的最低點。

一個轉移 \(f_{k,j-1}\to f_{i,j}\)，會有一個貢獻函數 \(\rm cost(l,r)\) 來表示這個代價。就是把 \([l,r]\) 的黑色折線翻折到紅色折線的上方的代價。其中這個紅色折線已經固定了，就是一個以 \((l,0)\) 和 \((r,0)\) 為兩個底部頂點的等腰直角三角形。

上文說過翻折一大段的代價就是其面積，所以黃色部分就是其代價。觀察一下圖形面積，一段向右下的線段能貢獻面積需要一段在 \(x\) 軸下方的向右上的線段。考慮如何計算這個面積，在坐標軸中根據直線方程分成兩段就是 \(\sum \max(x-l-s_x,0)+\sum \max(r-x-s_x,0)\)，暴力轉移是 \(O(n^3)\) 的。

觀察到 \(f\) 的第二維關于 \(k\) 是凸的，可以 wqs 二分處理掉。

同時 \(\rm cost(l,r)\) 滿足四邊形不等式，我們可以用二分隊列轉移，這個時候時間復雜度為 \(O(n\log^2 V)\)。可惜 \(2\log\) 過不去。

\(\rm cost(l,r)\) 函數其實是可以改寫成一個去掉 \(\max\) 的形式的，因為單次 \(s_x\) 最多變化 \(1\)，所以 \(x-l-s_x\) 是單調遞增的，能使其 \(\ge 0\) 的位置是一段后綴。對于 \(r-x-s_x\) 同理。我們提前處理出來這兩個轉折點，就可以拆掉 \(\max\) 寫成斜率優化的形式了。

寫成斜率優化的形式之后就可以丟掉一個 \(\log\) 了。時間復雜度 \(O(n\log V)\)。

其實上述又帶 \(l\) 又帶 \(r\) 的式子很復雜，把坐標軸旋轉 \(45°\) 之后再計算這個貢獻會變成很簡單！這啟發我們在求解這種 \(01\) 序列的時候，觀察性質用走斜線畫圖，計算貢獻用旋轉 \(45°\) 之后的方格圖來算。

P11420 [清華集訓 2024] 乘積的期望

Trick：對于定長度區間操作經常可以轉化為網格圖平衡復雜度，印象中 QOJ4893. Imbalance 也是的。

考慮將 \(n\) 個元素劃分成如下的網格圖（\(n\) 不是 \(m\) 的倍數的時候就補 \(b_i=0\) 湊成一個完整的圖）。

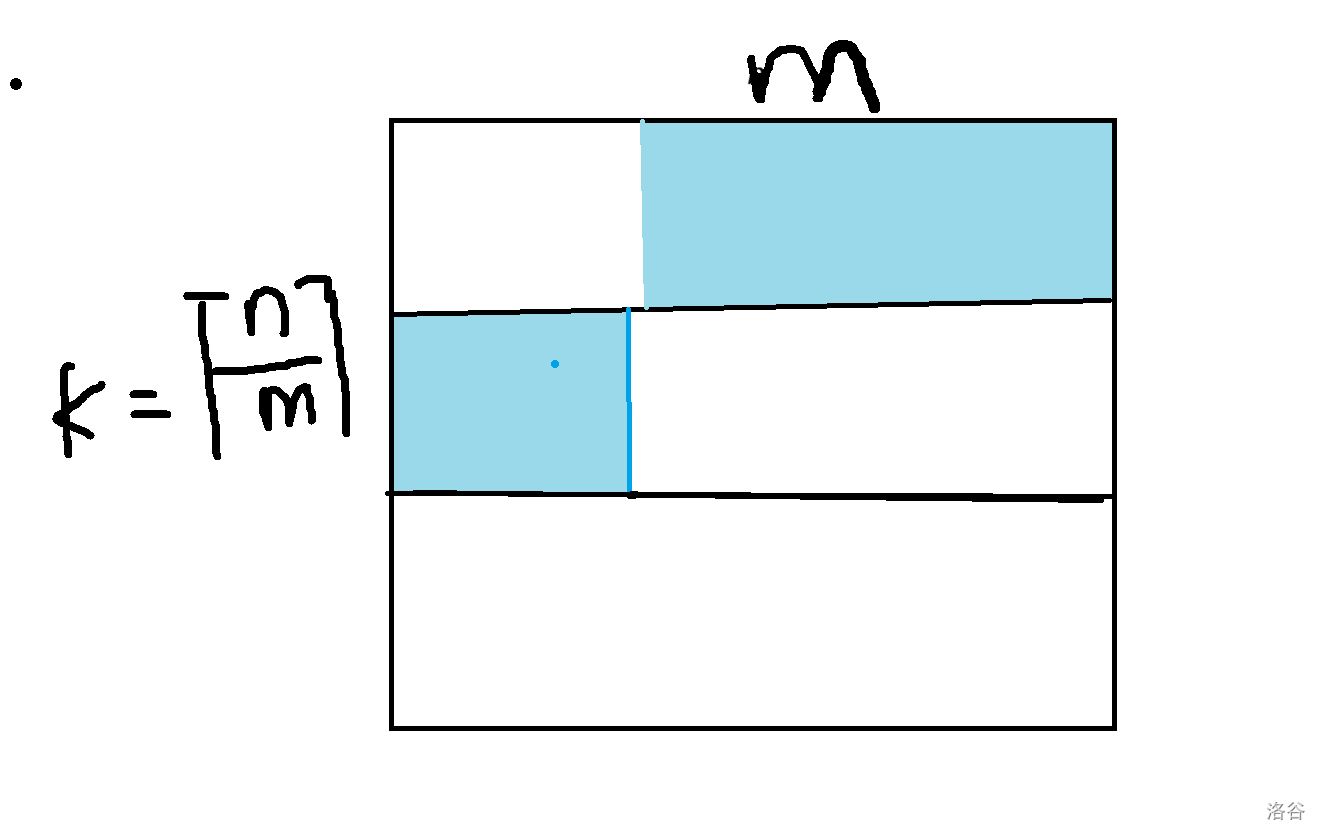
可以發現每次選擇 \(m\) 個連續的位置一定是某一行的后綴搭配上下一行的前綴，如圖中藍色部分。

有兩種轉移方式，一種是從上往下行間轉移，另一種是從左往右在列上面進行轉移。如果我們能找到兩種轉移方式就能平衡復雜度。

首先，將所有元素乘積的期望轉化成組合意義，也就是對于所有覆蓋方案我們都對于每個位置選擇一種覆蓋其的操作的總方案數。我們可以對著這個進行 DP。

豎向 DP

思考一下 DP 需要記錄哪些狀態，首先有記錄當前的位置 \(i\)，其次還有當前有幾條操作線段延伸過來了，可以我們發現這還不夠，無法刻畫長度為 \(m\) 這個約束。于是把這個改為一個 \(m\) 位的二進制數 \(s\)，記錄該位置往前的 \(m\) 個位置中有哪些作為線段的開頭，這還不行，因為可能有多個線段共用一個開頭，其實這個約束可以改為選這個線段的第一個元素。所以就變成了，某個位置是否是一條線段中被選擇的第一個位置，這樣子在一個位置上只會和一條線段有關，就可以用 \(01\) 變量記錄了，這樣子我們只需要約束選這個線段的第一個元素和最后一個元素距離 \(\le k\) 即可。

這樣子我們就可以根據信息開閉線段了。同時，我們發現上述過程并沒有對于所有線段作出區分，于是記錄一下我們已經選了的線段數量 \(j\)，這樣子最后為了讓這些線段可區分，我們就乘以 \(A^j_C\times (\sum b_i)^{m-j}\) 的系數。最后除以 \((\sum b_i)^m\) 即可。

設計好了狀態，現在需要進行 dp。考慮當前這一個位置 \(i\)，我們要為其選擇一個覆蓋它的線段（不考慮無線段覆蓋它的情況，因為這種情況的貢獻為 \(0\)）。

首先，如果 \(i-m+1\) 這個位置被選擇了開頭第一個元素，但是沒有選擇收尾元素，我們就必須選擇這條線段，因為這條線段最遠也就延伸到 \(i\)，而我們加入的時候已經欽定過其有結尾元素了，所以必須要為它找一個結尾元素，那么就只能選擇 \(i\) 了。

否則，我們可以自由選擇。第一個選擇就是在 \(i\) 這個位置新開一條線段（不一定以 \(i\) 作為左端點，但是 \(i\) 一定是其第一個元素），注意這個線段有兩種選擇，要么在這里終結，也就是說開頭結尾都是 \(i\)；要么往后延伸，也就說我們還要為其找一個 \(\neq i\) 的結尾。

如果不選擇新開線段，我們可以為其挑選一個之前開的線段，欽定其覆蓋 \(i\)。這里還有兩種選擇，一種是這條線段在 \(i\) 終結，也就是說 \(i\) 是其最后一個元素，注意由于我們加入線段的時候沒有為其選擇左端點 \(l\)，所以在終結的時候要選擇一個，假設其第一個位置是 \(j\)，那么左端點的范圍就是 \([i-m+1,j]\)，求一下區間 \(\sum b_i\) 作為系數即可。如果這條線段不在這里終結，那很簡單，正常轉移就行了。

分析一下時間復雜度，狀態數 \(O(nc2^m)\)。注意到最多有 \(O(n)\) 條線段被選擇，所以狀態數可以被優化到 \(O(n^22^m)\)，轉移是 \(O(m)\) 的，所以是 \(O(n^2m2^m)\)。當 \(2m>n\) 的時候，中間的 \(2m-n\) 個元素會被所有操作都覆蓋一次，所以這部分貢獻可以直接算的，是 \(c^{2m-n}\)，然后把這些部分去掉，就可以讓 \(2m\le n\) 了。所以指數可以對于 \(\dfrac{n}{2}\) 取 \(\min\)，最后的復雜度就是 \(O(n^2m2^{\min(m,\frac{n}{2})})\)。分析一下分數表格，發現在指數為 \(16\) 左右的時候是可以過的，因此這個做法是可以做 \(m\le 16\) 或者 \(n\le30\) 的測試點。這樣子可以得到 \(60\rm pts\)。

橫向 DP

上述做法可以通過 \(m\le 16\) 或者 \(n\le 30\) 的部分分，所以剩下的數據范圍就是 \(m\ge 17\) 且 \(31\le n\le 50\)，可以發現這個時候本題解配圖中的 \(k=\lceil \dfrac{n}{m}\rceil=3\)，也就是說網格圖分為三列。而我們橫著做 DP，就是每次的狀態是一列。

嘗試觀察一些刻畫方式，可以發現每次操作必然是對于每一列的三個位置中恰好有一個位置被操作。所以 \(a_i+a_{i+m}+a_{i+2m}=m\)。

還有就是基本上所有線段都是跨越兩行的，這會導致交界處被覆蓋次數很多。所以第一行中的 \(a_i\) 單調遞增，第三行中的 \(a_i\) 單調遞減。

這兩個條件足夠了嗎？并不是的。還有一個約束就是你會發現，要么一次操作是行內的，要么一二聯動，要么二三聯動，唯獨沒有一三聯動的情況，所以 \(a_m+a_{2m+1}\le C\)。

可以證明這三個條件已經是充要條件了。可以對于這個結構按照列進行 DP。

對于第三個約束，我們直接外層枚舉 \(a_m\) 就可以解決了。對于第一個約束告訴了我們，我們只需要記錄三個位置中的其中兩個位置的值，然后第三個位置的值就可以通過做差直接得到了。那么是記錄哪兩個位置呢？為了方便限制第二個約束，我們記錄第一行和第三行的就就行了。設 \(f_{i,j,k}\) 表示 dp 到了第 \(i\) 列，其中 \(a_i=j,a_{i+2m}=k\) 的方案數。

轉移的時候，枚舉 \(j'\ge j\) 和 \(k'\le k\) 進行轉移即可。直接做的時間復雜度是 \(O(nC^5)\)。

有一個小 trick 就是，你發現 \(j,k\) 之間是相對獨立的，所以你可以分開轉移 \(j,k\)，也就是說 \((j,k)\to (j',k)\to (j',k')\)，這樣子就優化到了 \(O(nC^4)\)。可以拿到 \(90 \rm pts\)。

發現瓶頸在于 \(C\) 很大，有一個觀察就是你在豎向 DP 的時候，會發現整個 DP 過程都是和 \(C\) 無關的，只有最后乘以組合數的時候才涉及 \(C\)，最后是一個關于 \(C\) 的 \(1\) 到 \(n\) 次的多項式求和，所以最終的答案關于 \(C\) 是一個 \(n+1\) 次多項式。于是我們算出 \(C\in [1,n+2]\) 的答案，然后進行拉格朗日插值即可。

這部分的時間復雜度是 \(O(n^6)\)。

兩個做法綜合起來可以通過本題。

CF1637H Minimize Inversions Number

選擇單個元素 \(p_i\)，逆序對數會變化 \(\sum\limits_{j<i}[p_j<p_i]-\sum\limits_{j<i}[p_j>p_i]\)，記為 \(w_i\)。

選擇多個元素，下標序列為 \(a_1,a_2...a_k\)，變化 \(\sum w_{a_i}+2\times [逆序對數-順序對數]\)。

其中逆序對數 \(-\) 順序對數可以轉化為 \(2\times [逆序對數]-{k\choose 2}\)。

嘗試打表，可以發現選擇 \(i+1\) 個數的方案恰好是選 \(i\) 個數的方案基礎上再選擇一個數。

有了這個觀察就很好做了，我們只需要滿足單步最優，累計起來就是多步最優了。否則你很難刻畫選擇子序列一堆數中逆序對數。

直接動態維護加入每個 \(a_i\)，會產生多少代價，每次選擇最小代價的加入。難以單 \(\log\)。

需要發現一些性質，將每個點看成 \((i,p_i)\) 放到二維平面中。采用調整法，對于 \(i<j\)，選擇 \(p_j\) 一定是更優的。對于 \((i,p_i)\) 和 \((j,p_j)\) 為分界點，平面劃分出來的若干個區域進行分別討論即可，對于單個區域貢獻不劣。

于是上述加入某個數 \(p_i\) 之前，對于所有 \(j>i\) 且 \(p_j<p_i\) 的數已經被添加過了，所以上述第二項子序列逆序對數貢獻對于單個元素可以提前確定了，單個數的貢獻可以變成獨立的了，不會依賴于之前選擇了什么而變化，直接排序即可。時間復雜度 \(O(n\log n)\)。

打表

• 觀察答案的結構/性質。

• 找到充分必要條件。

• 構造題分析子問題。

QOJ9785.Shrooks

給定一個長度為 \(n\) 的未填滿排列 \(p\)，求有多少排列滿足對于 \(\forall i,j\)，都有 \(|p_i-p_j|+|i-j|\le n\)。其中 \(n\le 2\times 10^5\)。

可以發現這是一個很嚴的限制，考慮最難滿足的地方，\(1\) 和 \(n\) 肯定相鄰，\(n-1\) 和 \(1\) 的距離最多為 \(2\) 等等。嘗試打表，觀察一下，發現 \(1\) 和 \(n\) 必然是在序列中間的，然后小數和大數向外散開。以中間位置為劃分點，小數滿足遞增，大數滿足遞減。

放入小數 \(1\)，會限制大數的位置，放入大數 \(n\) 為限制小數的位置。可以進行 dp，根據形態要求可以把狀態數壓到 \(O(n)\)。

QOJ8546. Min or Max 2

給定排列 \(a,b\)，你手上有一個數對 \((x,y)\)，初始為 \((a_1,b_1)\)。依次從 \(2\to n\)，你每次可以讓 \((x,y)\to (\max(x,a_i),\max(y,b_i))\)，也可以讓 \((x,y)\to (\min(x,a_i),\min(y,b_i))\)。對于最后得到的所有 \((x,y)\)，求 \(|x-y|=k\) 的個數。\(k\) 取 \([0,n-1]\) 之內的 所有數。\(n\le 5\times 10^5\)。

打表可以發現滿足要求的 \((x,y)\) 必定是形成一個區間階梯狀，也就是對于每個 \(x\)，合法的 \(y\) 構成一個區間，且隨著 \(x\) 增大，這個也區間左右端點也不斷向右移動。

如何判定 \((x,y)\) 是否合法，對于 \(<x\) 設為 \(0\)，\(>x\) 設為 \(2\)，\(=x\) 設為 \(1\)。然后進行一個雙指針。可以放到線段樹上做動態 dp，求出所有邊界之后這題就做完了。

調整法

• 符合大多數位置，再進行微調。
• 每步不劣。

調整之后就是符合若干條件的子問題了。

嘗試弱化問題條件。

P11986 [JOIST 2025] 急救車 / Ambulance

四個醫院還是太復雜了，于是先弱化一下問題，將 \(4\) 個醫院變成 \(2\) 個，且兩個醫院處于對角線。

設第 \(i\) 個人到醫院 \((1,1)\) 的代價為 \(a_i\)，到醫院 \((L,L)\) 的代價為 \(b_i\)。可以發現 \(a_i+b_i\) 為一個定值，于是就是一個經典貪心，直接按照 \(a_i\) 排序后，前綴分配給醫院 \(1\)，后綴分配給醫院 \(2\)。

擴展到四個醫院，還是按照剛剛的對角線劃分。我們這次引入兩個對角線序列，\((1,1)\) 和 \((L,L)\) 一組，\((L,1)\) 和 \((1,L)\) 一組。對于第一組按照到 \((1,1)\) 的距離排序，對于第二組按照到 \((1,L)\) 的距離排序。

枚舉兩個序列中的前后綴分界點，可以將所有點分成四組，每一組中的點可以前往兩個地點。于是我們直接設計一個 dp，設 \(dp_{i,t}\) 表示考慮了這一組的中的前 \(i\) 個元素，第一個醫院用時為 \(t\) 的時候，第二個醫院的最小用時。對于四組分別 dp 之后，枚舉 \((1,1)\) 的用時，然后利用第一組和第二組的 dp 信息可以得到到 \((1,L)\) 和到 \((L,1)\) 的最小用時，利用第三組的 dp 信息可以得到 \((L,L)\) 的最小用時，再利用第四組的 dp 信息判定 \((L,L)\) 和 \((L,1)\) 當前的用時是否合法即可。

單次 dp 是 \(O(nT)\) 的，如果直接枚舉分界點就是 \(O(n^3T)\) 的。可以對于第一個分界點掃描線，維護下標為第二個分界點的前后綴 dp 值，這樣子就可以做到 \(O(n^2T)\) 了。

CF2023F Hills and Pits

弱化問題條件，全局 \([1,n]\)，固定起點終點。

UOJ949. 【UER #12】電網檢修

先觀察一下電子運動規律，自己模擬一下可以發現是左右交替撞相反運動方向的段，被撞過的段每次折返的時候都不會被撞了，會恰好順著電子運動趨勢。而且恰好是左邊撞一個右邊撞一個。根據這個觀察已經可以刻畫終態了。

那就看哪邊先被撞開唄，于是可以得出結論如果 \([1,i]\) 中 + 的個數（記其為 \(c\)） \(\le\) \([i+1,n]\) 中 - 的個數，那么電子會從左邊出去，根據 \([1,i]\) 均為 -，\([i+1,n]\) 中的前 \(c\) 個 - 變成 +。

P10197 [USACO24FEB] Minimum Sum of Maximums P

我們先對于邊界加兩個 \(+\infty\) 的數之后就是要最小化 \(\sum |a_i-a_{i+1}|\)。

需要調整一下最優子結構，對于兩個端點 \(L,R\)（假設 \(L\le R\)） 之間的數，假設已經確定了所選數的集合，肯定將這些數升序排序，假設排出來的為 \(a_1,a_2..a_k\)，代價為 \(|L-a_1|+|R-a_k|+a_k-a_1\)。可以發現 \(a_1\) 盡可能大，\(a_n\) 盡可能小的時候肯定是不劣的。

這個性質就很牛了，我們在同一段內填入的數字構成一個區間，否則用調整法把兩個相交區間內的極值交換一下可以更優。因此可以進行區間 dp。