本文主要是對劉建平的機器學習中的矩陣向量求導系列文章的整理和轉載，并融入了CSDN、知乎等平臺上相關文章要點的學習心得，主要參考鏈接附在文章結尾處。

求導定義與求導布局

矩陣求導引入

在高等數學里面，我們已經學過了標量對標量的求導，比如標量$y$對標量$x$的求導，可以表示為$\frac{\partial y}{\partial x}$。

有些時候，我們會有一組標量$y_i(i = 1, 2,\dots , m)$來對一個標量$x$求導，那么我們會得到一組標量求導的結果：$$\frac{\partial y_i}{\partial x}, i=1,2.,,,m$$

如果我們把這組標量寫成向量的形式，即維度為m的一個向量$\mathbf{y}$對一個標量$x$求導，那么結果也是一個m維的向量：$\frac{\partial \mathbf{y}}{\partial x}$。

可見，所謂向量對標量的求導，其實就是向量里的每個分量分別對標量求導，最后把求導的結果排列在一起，按一個向量表示而已。類似的結論也存在于標量對向量的求導，向量對向量的求導，向量對矩陣的求導，矩陣對向量的求導，以及矩陣對矩陣的求導等。

總而言之，所謂的矩陣向量求導本質上就是多元函數求導，僅僅是把函數的自變量，因變量以及標量求導的結果排列成了向量矩陣的形式，方便表達與計算，更加簡潔而已。

為了便于描述，后面如果沒有指明，則求導的自變量用$x$表示標量，$\mathbf{x}$表示n維向量，$\mathbf{X}$表示$m \times n$維度的矩陣，求導的因變量用$y$表示標量，$\mathbf{y}$表示m維向量，$\mathbf{Y}$表示$p \times q$維度的矩陣。

矩陣求導定義

根據求導的自變量和因變量是標量，向量還是矩陣，我們有9種可能的矩陣求導定義，如下：

自變量\因變量	標量$y$	向量$\mathbf{y}$	矩陣$\mathbf{Y}$
標量$x$	$\frac{\partial y}{\partial x}$	$\frac{\partial  \mathbf{y}}{\partial x}$	$\frac{\partial  \mathbf{Y}}{\partial x}$
向量$\mathbf{x}$	$\frac{\partial y}{\partial \mathbf{x}}$	$\frac{\partial  \mathbf{y}}{\partial \mathbf{x}}$	$\frac{\partial  \mathbf{Y}}{\partial \mathbf{x}}$
矩陣$\mathbf{X}$	$\frac{\partial y}{\partial \mathbf{X}}$	$\frac{\partial  \mathbf{y}}{\partial \mathbf{X}}$	$\frac{\partial  \mathbf{Y}}{\partial \mathbf{X}}$

這9種里面，標量對標量的求導高數里面就有，不需要我們單獨討論，在剩下的8種情況里面，本節先討論上圖中標量對向量或矩陣求導，向量或矩陣對標量求導，以及向量對向量求導這5種情況。另外三種向量對矩陣的求導，矩陣對向量的求導，以及矩陣對矩陣的求導在第3節再講。

現在我們回看前面講到的例子，維度為m的一個向量$\mathbf{y}$對一個標量$x$的求導，那么結果也是一個m維的向量：$\frac{\partial \mathbf{y}}{\partial x}$。這是我們表格里面向量對標量求導的情況。這里有一個問題沒有講到，就是這個m維的求導結果排列成的m維向量到底應該是列向量還是行向量？

這個問題的答案是：行向量或者列向量皆可！畢竟我們求導的本質只是把標量求導的結果排列起來，至于是按行排列還是按列排列都是可以的。但是這樣也有問題，在我們機器學習算法法優化過程中，如果行向量或者列向量隨便寫，那么結果就不唯一，亂套了。

為了解決這個問題，我們引入求導布局的概念。

矩陣向量求導布局

為了解決矩陣向量求導的結果不唯一，我們引入求導布局。最基本的求導布局有兩個：分子布局(numerator layout)和分母布局(denominator layout )。

• 對于分子布局來說，我們求導結果的維度以分子為主，比如對于我們上面對標量求導的例子，結果的維度和分子的維度是一致的。也就是說，如果向量$\mathbf{y}$是一個m維的列向量，那么求導結果$\frac{\partial \mathbf{y}}{\partial x}$也是一個m維列向量。如果向量$\mathbf{y}$是一個m維的行向量，那么求導結果$\frac{\partial \mathbf{y}}{\partial x}$也是一個m維行向量。
• 對于分母布局來說，我們求導結果的維度以分母為主，比如對于我們上面對標量求導的例子，如果向量$\mathbf{y}$是一個m維的列向量，那么求導結果$\frac{\partial \mathbf{y}}{\partial x}$是一個m維行向量。如果向量$\mathbf{y}$是一個m維的行向量，那么求導結果$\frac{\partial \mathbf{y}}{\partial x}$是一個m維的列向量向量。

可見，對于分子布局和分母布局的結果來說，兩者相差一個轉置。

再舉一個例子，標量$y$對矩陣$ \mathbf{X}$求導，那么如果按分母布局，則求導結果的維度和矩陣$X$的維度$m \times n$是一致的。如果是分子布局，則求導結果的維度為$n \times m$。

這樣，對于標量對向量或者矩陣求導，向量或者矩陣對標量求導這4種情況，對應的分子布局和分母布局的排列方式已經確定了。

稍微麻煩點的是向量對向量的求導，本文只討論列向量對列向量的求導，其他的行向量求導只是差一個轉置而已。比如m維列向量$\mathbf{y}$對n維列向量$\mathbf{x}$求導，它的求導結果在分子布局和分母布局各是什么呢？

對于這2個向量求導，那么一共有$mn$個標量對標量的求導。求導的結果一般是排列為一個矩陣。如果是分子布局，則矩陣的第一個維度以分子為準，即結果是一個$m \times n$的矩陣，如下：$$ \frac{\partial  \mathbf{y}}{\partial \mathbf{x}} = \left( \begin{array}{ccc} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \ldots & \frac{\partial y_1}{\partial x_n}\\  \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2} & \ldots & \frac{\partial y_2}{\partial x_n}\\   \vdots&  \vdots &  \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1}& \frac{\partial y_m}{\partial x_2} & \ldots & \frac{\partial y_m}{\partial x_n}  \end{array} \right)$$

上邊這個按分子布局的向量對向量求導的結果矩陣，我們一般叫做雅克比 (Jacobian)矩陣。

如果是按分母布局，則求導的結果矩陣的第一維度會以分母為準，即結果是一個$n \times m$的矩陣，如下：$$ \frac{\partial  \mathbf{y}}{\partial \mathbf{x}} = \left( \begin{array}{ccc} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_2}{\partial x_1}& \ldots & \frac{\partial y_m}{\partial x_1}\\  \frac{\partial y_1}{\partial x_2}& \frac{\partial y_2}{\partial x_2} & \ldots & \frac{\partial y_m}{\partial x_2}\\   \vdots&  \vdots &  \ddots & \vdots \\ \frac{\partial y_1}{\partial x_n}& \frac{\partial y_2}{\partial x_n} & \ldots & \frac{\partial y_m}{\partial x_n}  \end{array} \right)$$

上邊這個按分母布局的向量對向量求導的結果矩陣，我們一般叫做梯度矩陣。

有了布局的概念，我們對于上面5種求導類型，可以各選擇一種布局來求導。但是對于某一種求導類型，不能同時使用分子布局和分母布局求導。

但是在機器學習算法原理的資料推導里，我們并沒有看到說正在使用什么布局，也就是說布局被隱含了，這就需要自己去推演，比較麻煩。但是一般來說我們會使用一種叫混合布局的思路，即如果是向量或者矩陣對標量求導，則使用分子布局為準，如果是標量對向量或者矩陣求導，則以分母布局為準。對于向量對對向量求導，有些分歧，本文中會以分子布局的雅克比矩陣為主。

具體總結如下：

自變量\因變量	標量$y$	列向量$\mathbf{y}$	矩陣$\mathbf{Y}$
標量$x$	/	$\frac{\partial  \mathbf{y}}{\partial x}$ 分子布局：m維列向量（默認布局） 分母布局：m維行向量	$\frac{\partial  \mathbf{Y}}{\partial x}$ 分子布局：$p \times q$矩陣（默認布局） 分母布局：$q \times p$矩陣
列向量$\mathbf{x}$	$\frac{\partial y}{\partial \mathbf{x}}$ 分子布局：n維行向量 分母布局：n維列向量（默認布局）	$\frac{\partial  \mathbf{y}}{\partial \mathbf{x}}$ 分子布局：$m \times n$雅克比矩陣（默認布局） 分母布局：$n \times m$梯度矩陣	/
矩陣$\mathbf{X}$	$\frac{\partial y}{\partial \mathbf{X}}$ 分子布局：$n \times m$矩陣 分母布局：$m \times n$矩陣（默認布局）	/	/

矩陣向量求導基礎總結

有了矩陣向量求導的定義和默認布局，我們后續就可以對上表中的5種矩陣向量求導過程進行一些常見的求導推導并總結求導方法，并討論向量求導的鏈式法則。

定義法

上一節主要討論了向量矩陣求導的9種定義與求導布局的概念。本節就其中的標量對向量求導，標量對矩陣求導, 以及向量對向量求導這三種場景的基本求解思路進行討論。

對于本文中的標量對向量或矩陣求導這兩種情況，如上節所說，以分母布局為默認布局。向量對向量求導，以分子布局為默認布局。如遇到其他文章中的求導結果和本文不同，請先確認使用的求導布局是否一樣。另外，由于機器學習中向量或矩陣對標量求導的場景很少見，本文不會單獨討論這兩種求導過程。

用定義法求解標量對向量求導

標量對向量求導，嚴格來說是實值函數對向量的求導。即定義實值函數$f: R^{n} \to R$,自變量$\mathbf{x}$是n維向量，而輸出$y$是標量。對于一個給定的實值函數，如何求解$\frac{\partial y}{\partial \mathbf{x}}$呢？

首先我們想到的是基于矩陣求導的定義來做，由于所謂標量對向量的求導，其實就是標量對向量里的每個分量分別求導，最后把求導的結果排列在一起，按一個向量表示而已。那么我們可以將實值函數對向量的每一個分量來求導，最后找到規律，得到求導的結果向量。

首先我們來看一個簡單的例子：$y=\mathbf{a}^T\mathbf{x}$,求解$\frac{\partial \mathbf{a}^T\mathbf{x}}{\partial \mathbf{x}}$

根據定義，我們先對$\mathbf{x}$的第i個分量進行求導，這是一個標量對標量的求導，如下：$$\frac{\partial \mathbf{a}^T\mathbf{x}}{\partial x_i} = \frac{\partial \sum\limits_{j=1}^n a_jx_j}{\partial x_i} = \frac{\partial a_ix_i}{\partial x_i} =a_i$$

可見，對向量的第i個分量的求導結果就等于向量$\mathbf{a}$的第i個分量。由于我們是分子布局，最后所有求導結果的分量組成的是一個n維向量。那么其實就是向量$\mathbf{a}$。也就是說：$$\frac{\partial \mathbf{a}^T\mathbf{x}}{\partial \mathbf{x}} = \mathbf{a}$$

同樣的思路，我們也可以直接得到：$$\frac{\partial \mathbf{x}^T\mathbf{a}}{\partial \mathbf{x}} = \mathbf{a}$$

給一個簡單的測試，大家看看自己能不能按定義法推導出:$$\frac{\partial \mathbf{x}^T\mathbf{x}}{\partial \mathbf{x}} =2\mathbf{x}$$

再來看一個復雜一點點的例子：$y=\mathbf{x}^T\mathbf{A}\mathbf{x}$,求解$\frac{\partial \mathbf{x}^T\mathbf{A}\mathbf{x}}{\partial \mathbf{x}}$

我們對$\mathbf{x}$的第k個分量進行求導如下：$$\frac{\partial \mathbf{x}^T\mathbf{A}\mathbf{x}}{\partial x_k} = \frac{\partial \sum\limits_{i=1}^n\sum\limits_{j=1}^n x_iA_{ij}x_j}{\partial x_k} = \sum\limits_{i=1}^n A_{ik}x_i + \sum\limits_{j=1}^n A_{kj}x_j $$

這個第k個分量的求導結果稍微復雜些了，仔細觀察一下，第一部分是矩陣$\mathbf{A}$的第k列轉置后和$x$相乘得到，第二部分是矩陣$\mathbf{A}$的第k行和$x$相乘得到，排列好就是: $$\frac{\partial \mathbf{x}^T\mathbf{A}\mathbf{x}}{\partial \mathbf{x}} = \mathbf{A}^T\mathbf{x} + \mathbf{A}\mathbf{x}$$

從上面可以看出，定義法求導對于簡單的實值函數是很容易的，但是復雜的實值函數就算求出了任意一個分量的導數，要排列出最終的求導結果還挺麻煩的，因此我們需要找到其他的簡便一些的方法來整體求導，而不是每次都先去針對任意一個分量，再進行排列。

標量對向量求導的一些基本法則

在我們尋找一些簡單的方法前，我們簡單看下標量對向量求導的一些基本法則，這些法則和標量對標量求導的過程類似。

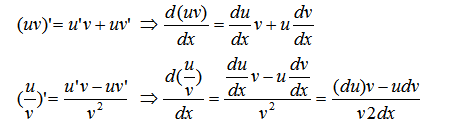
1)  常量對向量的求導結果為0。

2)  線性法則：如果$f,g$都是實值函數，$c_1,c_2$為常數，則：$$\frac{\partial (c_1f(\mathbf{x})+c_2g(\mathbf{x})}{\partial \mathbf{x}} = c_1\frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} +c_2\frac{\partial g(\mathbf{x})}{\partial \mathbf{x}} $$

3)  乘法法則：如果$f,g$都是實值函數，則：$$\frac{\partial f(\mathbf{x})g(\mathbf{x})}{\partial \mathbf{x}} = f(\mathbf{x})\frac{\partial g(\mathbf{x})}{\partial \mathbf{x}} +\frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} g(\mathbf{x}) $$

要注意的是如果不是實值函數，則不能這么使用乘法法則。

4)  除法法則：如果$f,g$都是實值函數，且$g(\mathbf{x}) \neq 0$，則：$$\frac{\partial f(\mathbf{x})/g(\mathbf{x})}{\partial \mathbf{x}} = \frac{1}{g^2(\mathbf{x})}(g(\mathbf{x})\frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} - f(\mathbf{x})\frac{\partial g(\mathbf{x})}{\partial \mathbf{x}})$$

用定義法求解標量對矩陣求導

現在我們來看看定義法如何解決標量對矩陣的求導問題。其實思路和2.2的標量對向量的求導是類似的，只是最后的結果是一個和自變量同型的矩陣。

我們還是以一個例子來說明。$y=\mathbf{a}^T\mathbf{X}\mathbf{b}$,求解$\frac{\partial \mathbf{a}^T\mathbf{X}\mathbf{b}}{\partial \mathbf{X}}$

其中, $\mathbf{a}$是m維向量,$\mathbf{b}$是n維向量,  $\mathbf{X}$是$m \times n$的矩陣。

我們對矩陣$\mathbf{X}$的任意一個位置的$X_{ij}$求導，如下：$$\frac{\partial \mathbf{a}^T\mathbf{X}\mathbf{b}}{\partial X_{ij}} =  \frac{\partial \sum\limits_{p=1}^m\sum\limits_{q=1}^n a_pA_{pq}b_q}{\partial X_{ij}} =  \frac{\partial  a_iA_{ij}b_j}{\partial X_{ij}} = a_ib_j$$

即求導結果在$(i.j)$位置的求導結果是$\mathbf{a}$向量第i個分量和$\mathbf{b}$第j個分量的乘積，將所有的位置的求導結果排列成一個$m \times n$的矩陣，即為$ab^T$,這樣最后的求導結果為：$$\frac{\partial \mathbf{a}^T\mathbf{X}\mathbf{b}}{\partial \mathbf{X}} = ab^T$$

簡單的求導的確不難，但是如果是比較復雜的標量對矩陣求導，比如$y=\mathbf{a}^Texp(\mathbf{X}\mathbf{b})$,對任意標量求導容易，排列起來還是蠻麻煩的，也就是我們遇到了和標量對向量求導一樣的問題，定義法比較適合解決簡單的問題，復雜的求導需要更簡便的方法。這個方法我們在下一節來講。

同時，標量對矩陣求導也有和第二節對向量求導類似的基本法則，這里就不累述了。

用定義法求解向量對向量求導

這里我們也同樣給出向量對向量求導的定義法的具體例子。

先來一個簡單的例子: $\mathbf{y} = \mathbf{A} \mathbf{x} $,其中$ \mathbf{A}$為$n \times m$的矩陣。$\mathbf{x}, \mathbf{y}$分別為$m,n$維向量。需要求導$\frac{\partial \mathbf{A}\mathbf{x}}{\partial \mathbf{x}}$,根據定義，結果應該是一個$n \times m$的矩陣。

先求矩陣的第i行和向量的內積對向量的第j分量求導，用定義法求解過程如下：$$\frac{\partial \mathbf{A_i}\mathbf{x}}{\partial \mathbf{x_j}} = \frac{\partial A_{ij}x_j}{\partial \mathbf{x_j}}= A_{ij}$$

可見矩陣 $\mathbf{A}$的第i行和向量的內積對向量的第j分量求導的結果就是矩陣 $\mathbf{A}$的$(i,j)$位置的值。排列起來就是一個矩陣了，由于我們分子布局，所以排列出的結果是$ \mathbf{A}$,而不是 $\mathbf{A}^T$。

定義法矩陣向量求導的局限

使用定義法雖然已經求出一些簡單的向量矩陣求導的結果，但是對于復雜的求導式子，則中間運算會很復雜，同時求導出的結果排列也是很頭痛的。下一節我們討論使用矩陣微分和跡函數的方法來求解矩陣向量求導。

矩陣向量求導之微分法

第2節主要討論了定義法求解矩陣向量求導的方法，但是這個方法對于比較復雜的求導式子，中間運算會很復雜，同時排列求導出的結果也很麻煩。因此我們需要其他的一些求導方法。本節我們討論使用微分法來求解標量對向量的求導，以及標量對矩陣的求導。

本文的標量對向量的求導，以及標量對矩陣的求導使用分母布局。如果遇到其他資料求導結果不同，請先確認布局是否一樣。

矩陣微分

在高數里面我們學習過標量的導數和微分，它們之間有這樣的關系：$\mathrmw0obha2h00f = f'(x)\mathrmw0obha2h00x$。如果是多變量的情況，則微分可以寫成：$$df=\sum\limits_{i=1}^n\frac{\partial f}{\partial x_i}dx_i = (\frac{\partial f}{\partial \mathbf{x}})^Td\mathbf{x}$$

從上次我們可以發現標量對向量的求導和它的向量微分有一個轉置的關系。

現在我們再推廣到矩陣。對于矩陣微分，我們的定義為：$$df=\sum\limits_{i=1}^m\sum\limits_{j=1}^n\frac{\partial f}{\partial X_{ij}}dX_{ij} = tr((\frac{\partial f}{\partial \mathbf{X}})^Td\mathbf{X})$$

其中第二步使用了矩陣跡的性質，即跡函數等于主對角線的和。即$$tr(A^TB) = \sum\limits_{i,j}A_{ij}B_{ij}$$

【推導注釋：矩陣微分到跡函數的詳細推導請點】

從上面矩陣微分的式子，我們可以看到矩陣微分和它的導數也有一個轉置的關系，不過在外面套了一個跡函數而已。由于標量的跡函數就是它本身，那么矩陣微分和向量微分可以統一表示，即：$$df= tr((\frac{\partial f}{\partial \mathbf{X}})^Td\mathbf{X})\;\; \;df= tr((\frac{\partial f}{\partial \mathbf{x}})^Td\mathbf{x})$$

矩陣微分的性質

我們在討論如何使用矩陣微分來求導前，先看看矩陣微分的性質：

1)  微分加減法：$d(X+Y) =dX+dY, d(X-Y) =dX-dY$

2)  微分乘法：$d(XY) =(dX)Y + X(dY)$

3)  微分轉置：$d(X^T) =(dX)^T$

4)  微分的跡：$dtr(X) =tr(dX)$

5)  微分哈達馬乘積： $d(X \odot Y) = X\odot dY + dX \odot Y$

6)  逐元素求導：$d \sigma(X) =\sigma'(X) \odot dX$

【公式注解：這里的$\sigma ()$是逐元素求導，即是對$X$中的每個元素各自做變換的函數。附哈達馬乘積詳解】

7)  逆矩陣微分：$d X^{-1}= -X^{-1}dXX^{-1}$

8)  行列式微分：$d |X|= |X|tr(X^{-1}dX)$　

【公式注解：行列式的導數】

有了這些性質，我們再來看看如何由矩陣微分來求導數。

使用微分法求解矩陣向量求導

由于3.1我們已經得到了矩陣微分和導數關系，現在我們就來使用微分法求解矩陣向量求導。

若標量函數$f$是矩陣$X$經加減乘法、逆、行列式、逐元素函數等運算構成，則使用相應的運算法則對$f$求微分，再使用跡函數技巧給$df$套上跡并將其它項交換至$dX$左側,那么對于跡函數里面在$dX$左邊的部分，我們只需要加一個轉置就可以得到導數了。

這里需要用到的跡函數的技巧主要有這么幾個：

            1)  標量的跡等于自己：$tr(x) =x$

            2)  轉置不變：$tr(A^T) =tr(A)$

            3)  交換率：$tr(AB) =tr(BA)$,需要滿足$A,B^T$同維度。

            4)  加減法：$tr(X+Y) =tr(X)+tr(Y), tr(X-Y) =tr(X)-tr(Y)$

            5) 矩陣乘法和跡交換：$tr((A\odot B)^TC)= tr(A^T(B \odot C))$,需要滿足$A,B,C$同維度。

我們先看第一個例子，我們使用上一篇定義法中的一個求導問題：$$y=\mathbf{a}^T\mathbf{X}\mathbf{b}, \frac{\partial y}{\partial \mathbf{X}}$$

首先，我們使用微分乘法的性質對$f$求微分，得到：$$dy = d\mathbf{a}^T\mathbf{X}\mathbf{b} + \mathbf{a}^Td\mathbf{X}\mathbf{b} + \mathbf{a}^T\mathbf{X}d\mathbf{b} = \mathbf{a}^Td\mathbf{X}\mathbf{b}$$ 【推導注解：常量的微分為0】

第二步，就是兩邊套上跡函數，即：$$dy =tr(dy) = tr(\mathbf{a}^Td\mathbf{X}\mathbf{b}) = tr(\mathbf{b}\mathbf{a}^Td\mathbf{X})$$

其中第一到第二步使用了上面跡函數性質1，第三步到第四步用到了上面跡函數的性質3。

根據我們矩陣導數和微分的定義，跡函數里面在$dX$左邊的部分$\mathbf{b}\mathbf{a}^T$,加上一個轉置即為我們要求的導數，即：$$\frac{\partial f}{\partial \mathbf{X}} = (\mathbf{b}\mathbf{a}^T)^T = \mathbf{ab}^T$$

以上就是微分法的基本流程，先求微分再做跡函數變換，最后得到求導結果。比起定義法，我們現在不需要去對矩陣中的單個標量進行求導了。

再來看看$$y=\mathbf{a}^Texp(\mathbf{X}\mathbf{b}), \frac{\partial y}{\partial \mathbf{X}}$$

$$dy =tr(dy) = tr(\mathbf{a}^Tdexp(\mathbf{X}\mathbf{b})) = tr(\mathbf{a}^T (exp(\mathbf{X}\mathbf{b}) \odot d(\mathbf{X}\mathbf{b}))) = tr((\mathbf{a}  \odot exp(\mathbf{X}\mathbf{b}) )^T d\mathbf{X}\mathbf{b}) =  tr(\mathbf{b}(\mathbf{a}  \odot exp(\mathbf{X}\mathbf{b}) )^T d\mathbf{X})  $$

其中第三步到第四步使用了上面跡函數的性質5。【推導注解：$exp(x)$的導數是其本身】

這樣我們的求導結果為：$$\frac{\partial y}{\partial \mathbf{X}} =(\mathbf{a}  \odot exp(\mathbf{X}\mathbf{b}) )b^T $$

以上就是微分法的基本思路。

【推導注解：標量的跡等于自身，所以標量函數的微分都可以直接套上跡來算】

跡函數對向量矩陣求導

由于微分法使用了跡函數的技巧，那么跡函數對對向量矩陣求導這一大類問題，使用微分法是最簡單直接的。下面給出一些常見的跡函數的求導過程，也順便給大家熟練掌握微分法的技巧。

首先是$\frac{\partial tr(AB)}{\partial A} = B^T, \frac{\partial tr(AB)}{\partial B} =A^T$,這個直接根據矩陣微分的定義即可得到。

再來看看$\frac{\partial tr(W^TAW)}{\partial W}$:$$d(tr(W^TAW)) = tr(dW^TAW +W^TAdW) = tr(dW^TAW)+tr(W^TAdW) = tr((dW)^TAW) + tr(W^TAdW) = tr(W^TA^TdW) +  tr(W^TAdW) = tr(W^T(A+A^T)dW) $$

因此可以得到：$$\frac{\partial tr(W^TAW)}{\partial W} = (A+A^T)W$$

最后來個更加復雜的跡函數求導：$\frac{\partial tr(B^TX^TCXB)}{\partial X} $: $$d(tr(B^TX^TCXB)) = tr(B^TdX^TCXB) + tr(B^TX^TCdXB) = tr((dX)^TCXBB^T) + tr(BB^TX^TCdX) = tr(BB^TX^TC^TdX) + tr(BB^TX^TCdX) = tr((BB^TX^TC^T + BB^TX^TC)dX)$$

因此可以得到：$$\frac{\partial tr(B^TX^TCXB)}{\partial X}= (C+C^T)XBB^T$$

【推導注解：多次用到了跡函數轉置不變的技巧】

微分法求導小結

使用矩陣微分，可以在不對向量或矩陣中的某一元素單獨求導再拼接，因此會比較方便，當然熟練使用的前提是對上面矩陣微分的性質，以及跡函數的性質熟練運用。

【結論注解：對于未提及的向量對向量求導在分母布局時與微分存在轉置關系，而在分子布局時相等。】

還有一些場景，求導的自變量和因變量直接有復雜的多層鏈式求導的關系，此時微分法使用起來也有些麻煩。如果我們可以利用一些常用的簡單求導結果，再使用鏈式求導法則，則會非常的方便。因此下一節我們討論向量矩陣求導的鏈式法則。

矩陣向量求導鏈式法則

第3節討論了使用微分法來求解矩陣向量求導的方法。但是很多時候，求導的自變量和因變量直接有復雜的多層鏈式求導的關系，此時微分法使用起來也有些麻煩。需要一些簡潔的方法。本文我們討論矩陣向量求導鏈式法則，使用該法則很多時候可以幫我們快速求出導數結果。

本節的標量對向量的求導，標量對矩陣的求導使用分母布局， 向量對向量的求導使用分子布局。如果遇到其他資料求導結果不同，請先確認布局是否一樣。

向量對向量求導的鏈式法則

首先我們來看看向量對向量求導的鏈式法則。假設多個向量存在依賴關系，比如三個向量$\mathbf{x} \to \mathbf{y} \to \mathbf{z}$存在依賴關系，則我們有下面的鏈式求導法則：$$\frac{\partial \mathbf{z}}{\partial \mathbf{x}} = \frac{\partial \mathbf{z}}{\partial \mathbf{y}}\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$$

該法則也可以推廣到更多的向量依賴關系。但是要注意的是要求所有有依賴關系的變量都是向量，如果有一個$\mathbf{Y}$是矩陣，，比如是$\mathbf{x} \to \mathbf{Y} \to \mathbf{z}$， 則上式并不成立。

從矩陣維度相容的角度也很容易理解上面的鏈式法則，假設$\mathbf{x} , \mathbf{y} ,\mathbf{z}$分別是$m, n, p$維向量，則求導結果$\frac{\partial \mathbf{z}}{\partial \mathbf{x}}$是一個$p \times m$的雅克比矩陣，而右邊$\frac{\partial \mathbf{z}}{\partial \mathbf{y}}$是一個$p \times n$的雅克比矩陣，$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$是一個$n \times m$的矩陣，兩個雅克比矩陣的乘積維度剛好是$p \times m$，和左邊相容。

標量對多個向量的鏈式求導法則

在我們的機器學習算法中，最終要優化的一般是一個標量損失函數，因此最后求導的目標是標量，無法使用上面的鏈式求導法則，比如2向量，最后到1標量的依賴關系：$\mathbf{x} \to \mathbf{y} \to z$，此時很容易發現維度不相容。

假設$\mathbf{x} , \mathbf{y} $分別是$m,n$維向量, 那么$\frac{\partial z}{\partial \mathbf{x}}$的求導結果是一個$m \times 1$的向量, 而$\frac{\partial z}{\partial \mathbf{y}}$是一個$n \times 1$的向量，$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$是一個$n \times m$的雅克比矩陣,右邊的向量和矩陣是沒法直接乘的。

但是假如我們把標量求導的部分都做一個轉置，那么維度就可以相容了，也就是：$$(\frac{\partial z}{\partial \mathbf{x}})^T = (\frac{\partial z}{\partial \mathbf{y}})^T\frac{\partial \mathbf{y}}{\partial \mathbf{x}} $$

但是畢竟我們要求導的是$(\frac{\partial z}{\partial \mathbf{x}})$,而不是它的轉置，因此兩邊轉置我們可以得到標量對多個向量求導的鏈式法則：$$\frac{\partial z}{\partial \mathbf{x}} = (\frac{\partial \mathbf{y}}{\partial \mathbf{x}} )^T\frac{\partial z}{\partial \mathbf{y}}$$

如果是標量對更多的向量求導,比如$\mathbf{y_1} \to \mathbf{y_2}  \to …\to  \mathbf{y_n} \to z$，則其鏈式求導表達式可以表示為：$$\frac{\partial z}{\partial \mathbf{y_1}} = (\frac{\partial \mathbf{y_n}}{\partial \mathbf{y_{n-1}}} \frac{\partial \mathbf{y_{n-1}}}{\partial \mathbf{y_{n-2}}} …\frac{\partial \mathbf{y_2}}{\partial \mathbf{y_1}})^T\frac{\partial z}{\partial \mathbf{y_n}}$$

這里我們給一個最常見的最小二乘法求導的例子。最小二乘法優化的目標是最小化如下損失函數:$$l=(X\theta – y)^T(X\theta – y)$$

我們優化的損失函數$l$是一個標量，而模型參數$\theta$是一個向量，期望$\ell$對$\theta$求導，并求出導數等于0時候的極值點。我們假設向量$z = X\theta – y$, 則$l=z^Tz$， $\theta \to z \to l$存在鏈式求導的關系，因此：$$\frac{\partial l}{\partial \mathbf{\theta}} = (\frac{\partial z}{\partial \theta} )^T\frac{\partial l}{\partial \mathbf{z}} = X^T(2z) =2X^T(X\theta – y)$$

其中最后一步轉換使用了如下求導公式：$$\frac{\partial X\theta – y}{\partial \theta} = X$$ $$\frac{\partial z^Tz}{\partial z} = 2z$$

這兩個式子我們在前幾篇里已有求解過，現在可以直接拿來使用了，非常方便。

當然上面的問題使用微分法求導數也是非常簡單的，這里只是給出鏈式求導法的思路。

標量對多個矩陣的鏈式求導法則

下面我們再來看看標量對多個矩陣的鏈式求導法則，假設有這樣的依賴關系：$\mathbf{X} \to \mathbf{Y} \to z$，那么我們有：$$\frac{\partial z}{\partial x_{ij}} = \sum\limits_{k,l}\frac{\partial z}{\partial Y_{kl}} \frac{\partial Y_{kl}}{\partial X_{ij}} =tr((\frac{\partial z}{\partial Y})^T\frac{\partial Y}{\partial X_{ij}})$$

這里大家會發現我們沒有給出基于矩陣整體的鏈式求導法則，主要原因是矩陣對矩陣的求導是比較復雜的定義，我們目前也未涉及。因此只能給出對矩陣中一個標量的鏈式求導方法。這個方法并不實用，因為我們并不想每次都基于定義法來求導最后再去排列求導結果。

雖然我們沒有全局的標量對矩陣的鏈式求導法則，但是對于一些線性關系的鏈式求導，我們還是可以得到一些有用的結論的。

【神經網絡經典范例】

我們來看這個常見問題：$A,X,B,Y$都是矩陣，$z$是標量，其中$z= f(Y), Y=AX+B$,我們要求出$\frac{\partial z}{\partial X}$，這個問題在機器學習中是很常見的。此時，我們并不能直接整體使用矩陣的鏈式求導法則，因為矩陣對矩陣的求導結果不好處理。

這里我們回歸初心，使用定義法試一試,先使用上面的標量鏈式求導公式：$$\frac{\partial z}{\partial x_{ij}}  = \sum\limits_{k,l}\frac{\partial z}{\partial Y_{kl}} \frac{\partial Y_{kl}}{\partial X_{ij}}$$

我們再來看看后半部分的導數：$$ \frac{\partial Y_{kl}}{\partial X_{ij}} =  \frac{\partial \sum\limits_s(A_{ks}X_{sl})}{\partial X_{ij}} =   \frac{\partial A_{ki}X_{il}}{\partial X_{ij}} =A_{ki}\delta_{lj}$$

其中$\delta_{lj}$在$l = j$時為$1$，否則為$0$。

那么最終的標簽鏈式求導公式轉化為：$$\frac{\partial z}{\partial x_{ij}}  = \sum\limits_{k,l}\frac{\partial z}{\partial Y_{kl}} A_{ki}\delta_{lj} =  \sum\limits_{k}\frac{\partial z}{\partial Y_{kj}} A_{ki}$$

即矩陣$A^T$的第i行和$\frac{\partial z}{\partial Y} $的第j列的內積。排列成矩陣即為：$$\frac{\partial z}{\partial X} = A^T\frac{\partial z}{\partial Y}$$

總結下就是：$$z= f(Y), Y=AX+B \to \frac{\partial z}{\partial X} = A^T\frac{\partial z}{\partial Y}$$

這結論在$\mathbf{x}$是一個向量的時候也成立，即：$$z= f(\mathbf{y}), \mathbf{y}=A\mathbf{x}+\mathbf{b} \to \frac{\partial z}{\partial \mathbf{x}} = A^T\frac{\partial z}{\partial \mathbf{y}}$$

如果要求導的自變量在左邊，線性變換在右邊，也有類似稍有不同的結論如下，證明方法是類似的，這里直接給出結論：$$z= f(Y), Y=XA+B \to \frac{\partial z}{\partial X} = \frac{\partial z}{\partial Y}A^T$$ $$z= f(\mathbf{y}), \mathbf{y}=X\mathbf{a}+\mathbf{b} \to \frac{\partial z}{\partial \mathbf{X}} = \frac{\partial z}{\partial \mathbf{y}}a^T$$

使用好上述四個結論，對于機器學習尤其是深度學習里的求導問題可以非常快的解決,大家可以試一試。

矩陣向量求導小結

矩陣向量求導在前面我們討論三種方法，定義法，微分法和鏈式求導法。在同等情況下，優先考慮鏈式求導法，尤其是第三節的四個結論。其次選擇微分法、在沒有好的求導方法的時候使用定義法是最后的保底方案。

基本上大家看了系列里這四篇后對矩陣向量求導就已經很熟悉了，對于機器學習中出現的矩陣向量求導問題已足夠。這里還沒有講到的是矩陣對矩陣的求導，還有矩陣對向量，向量對矩陣求導這三種形式，將在第5節簡單討論一下，如果大家只是關注機器學習的優化問題，不涉及其他應用數學問題的，可以不關注。

矩陣對矩陣的求導

前4節我們主要討論了標量對向量矩陣的求導，以及向量對向量的求導。本文我們就討論下之前沒有涉及到的矩陣對矩陣的求導，還有矩陣對向量，向量對矩陣求導這幾種形式的求導方法。

本節所有求導布局以分母布局為準，為了適配矩陣對矩陣的求導，本文向量對向量的求導也以分母布局為準，這和前面的文章不同，需要注意。

本節主要參考了張賢達的《矩陣分析與應用》和長軀鬼俠的矩陣求導術

矩陣對矩陣求導的定義

假設我們有一個$p \times q$的矩陣$F$要對$m \times n$的矩陣$X$求導，那么根據我們第1節求導的定義，矩陣$F$中的$pq$個值要對矩陣$X$中的$mn$個值分別求導，那么求導的結果一共會有$mnpq$個。那么求導的結果如何排列呢？方法有很多種。

最直觀可以想到的求導定義有2種：

第一種是矩陣$F$對矩陣$X$中的每個值$X_{ij}$求導，這樣對于矩陣$X$每一個位置$(i, j)$求導得到的結果是一個矩陣$\frac{\partial F}{\partial X_{ij}}$，可以理解為矩陣$X$的每個位置都被替換成一個$p \times q$的矩陣，最后我們得到了一個$mp \times nq$的矩陣。

第二種和第一種類似，可以看做矩陣$F$中的每個值$F_{kl}$分別對矩陣$X$求導，這樣矩陣$F$每一個位置(k,l)對矩陣$X$求導得到的結果是一個矩陣$\frac{\partial F_{kl}}{\partial X}$, 可以理解為矩陣$F$的每個位置都被替換成一個$m \times n$的矩陣，最后我們得到了一個$mp \times nq$的矩陣。

這兩種定義雖然沒有什么問題，但是很難用于實際的求導，比如類似我們在第3節中很方便使用的微分法求導。

目前主流的矩陣對矩陣求導定義是對矩陣先做向量化，然后再使用向量對向量的求導。而這里的向量化一般是使用列向量化。也就是說，現在我們的矩陣對矩陣求導可以表示為：$$\frac{\partial F}{\partial X} = \frac{\partial vec(F)}{\partial vec(X)}$$

對于矩陣$F$，列向量化后，$vec(F)$的維度是$pq \times 1$的向量，同樣的，$vec(X)$的維度是$mn \times 1$的向量。最終求導的結果，這里我們使用分母布局，得到的是一個$mn \times pq$的矩陣。

矩陣對矩陣求導的微分法

按第一節的向量化的矩陣對矩陣求導有什么好處呢？主要是為了使用類似于前面講過的微分法求導。回憶之前標量對向量矩陣求導的微分法里，我們有：$$df= tr((\frac{\partial f}{\partial \mathbf{X}})^Td\mathbf{X})$$

這里矩陣對矩陣求導我們有：$$vec(dF) =\frac{\partial vec(F)^T}{\partial vec(X)} vec(dX) = \frac{\partial F^T}{\partial X} vec(dX)$$

和之前標量對矩陣的微分法相比，這里的跡函數被矩陣向量化代替了。

矩陣對矩陣求導的微分法，也有一些法則可以直接使用。主要集中在矩陣向量化后的運算法則，以及向量化和克羅內克積之間的關系。關于矩陣向量化和克羅內克積，具體可以參考張賢達的《矩陣分析與應用》，這里只給出微分法會用到的常見轉化性質, 相關證明可以參考張的書。

矩陣向量化的主要運算法則有：

    1)  線性性質：$vec(A+B) =vec(A) +vec(B)$

    2)  矩陣乘法：$vec(AXB)= (B^T \bigotimes A)vec(X)$,其中$\bigotimes$是克羅內克積。

    3)  矩陣轉置：$vec(A^T) =K_{mn}vec(A)$,其中$A$是$m \times n$的矩陣，$K_{mn}$是$mn \times mn$的交換矩陣，用于矩陣列向量化和行向量化之間的轉換。

    4)  逐元素乘法：$vec(A \odot X) = diag(A)vec(X)$, 其中$diag(A)$是$mn \times mn$的對角矩陣，對角線上的元素是矩陣$A$按列向量化后排列出來的。

克羅內克積的主要運算法則有：

    1)  $(A \bigotimes B)^T = A^T \bigotimes B^T$

    2)  $vec(ab^T) = b \bigotimes a$

    3)  $(A \bigotimes B)(C \bigotimes D )=AC \bigotimes BD$

    4)  $K_{mn} = K_{nm}^T, K_{mn}K_{nm}=I$

使用上面的性質，求出$vec(dF)$關于$ vec(dX)$的表達式，則表達式左邊的轉置即為我們要求的$\frac{\partial vec(F)}{\partial vec(X)} $,或者說$\frac{\partial F}{\partial X} $

矩陣對矩陣求導實例

下面我們給出一個使用微分法求解矩陣對矩陣求導的實例。

首先我們來看看：$\frac{\partial AXB}{\partial X}$, 假設$A,X,B$都是矩陣，$X$是$m \times n$的矩陣。

首先求$dF$, 和之前第3節的微分法類似，我們有: $$dF =AdXB$$

然后我們兩邊列向量化(之前的微分法是套上跡函數), 得到：$$vec(dF) = vec(AdXB) = (B^T \bigotimes A)vec(dX)$$

其中，第二個式子使用了上面矩陣向量化的性質2。

這樣，我們就得到了求導結果為：$$\frac{\partial AXB}{\partial X} =  (B^T \bigotimes A)^T = B \bigotimes A^T$$

利用上面的結果我們也可以得到：$$\frac{\partial AX}{\partial X} =  I_n \bigotimes A^T$$$$\frac{\partial XB}{\partial X} =  B \bigotimes I_m$$

來個復雜一些的：$\frac{\partial Aexp(BXC)D}{\partial X}$

首先求微分得到：$$dF =A [dexp(BXC)]D = A[exp(BXC) \odot (BdXC)]D  $$

兩邊矩陣向量化，我們有：$$vec(dF) = (D^T \bigotimes A) vec[exp(BXC) \odot (BdXC)]  =  (D^T \bigotimes A) diag(exp(BXC))vec(BdXC) =  (D^T \bigotimes A) diag(exp(BXC))(C^T\bigotimes B)vec(dX) $$

其中第一個等式使用了矩陣向量化性質2，第二個等式使用了矩陣向量化性質4， 第三個等式使用了矩陣向量化性質2。

這樣我們最終得到：$$\frac{\partial Aexp(BXC)D}{\partial X} = [(D^T \bigotimes A) diag(exp(BXC))(C^T\bigotimes B)]^T = (C \bigotimes B^T) diag(exp(BXC)) (D\bigotimes A^T )$$

矩陣對矩陣求導小結

由于矩陣對矩陣求導的結果包含克羅內克積，因此和之前我們講到的其他類型的矩陣求導很不同，在機器學習算法優化中中，我們一般不在推導的時候使用矩陣對矩陣的求導，除非只是做定性的分析。如果遇到矩陣對矩陣的求導不好繞過，一般可以使用4.3最后的幾個鏈式法則公式來避免。

到此機器學習中的矩陣向量求導系列就寫完了，希望可以幫到對矩陣求導的推導過程感到迷茫的同學們。

以上所有內容的細節補充請點。

參考資料：

http://www.rzrgm.cn/pinard/p/10750718.html

http://www.rzrgm.cn/pinard/p/10773942.html

http://www.rzrgm.cn/pinard/p/10791506.html

http://www.rzrgm.cn/pinard/p/10825264.html

http://www.rzrgm.cn/pinard/p/10930902.html