藍橋杯[第十一屆][B組]-平面切分
2022-04-04 18:25 幻霞 閱讀(117) 評論(0) 收藏 舉報這題用到歐拉定理
所以筆者去查了一下:https://baike.sogou.com/v163464.htm?fromTitle=%E6%AC%A7%E6%8B%89%E5%AE%9A%E7%90%86&ch=frombaikevr
歐拉是個著名的各種家,提出的理論有很多,非常厲害,這也導致筆者花了不少時間去找相關的結(jié)論。
結(jié)論如下:
歐拉發(fā)現(xiàn),不論什么形狀的凸多面體,其頂點數(shù)V、棱數(shù)E、面數(shù)F之間總有關系V+F-E=2,此式稱為歐拉公式。V+F-E即歐拉示性數(shù),已成為“拓撲學”的基礎概念。
這個和平面唯一的不同就是這是三維的結(jié)論,而該題是二維的,那么怎么辦?其實我們可以把當前題目構(gòu)成的圖形按著一個規(guī)律升維,比如
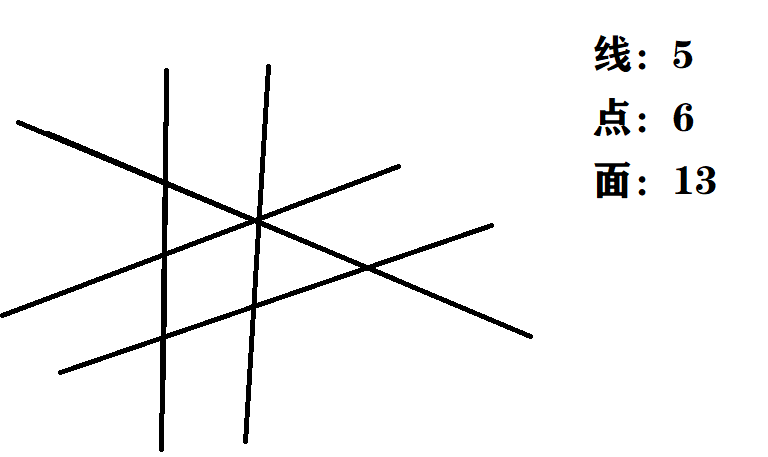
這個圖形其實我們可以把線延長然后把它們連起來(這是直線,但為了方便處理,定義一個邊界,把它們連起來)
結(jié)果就是這樣:
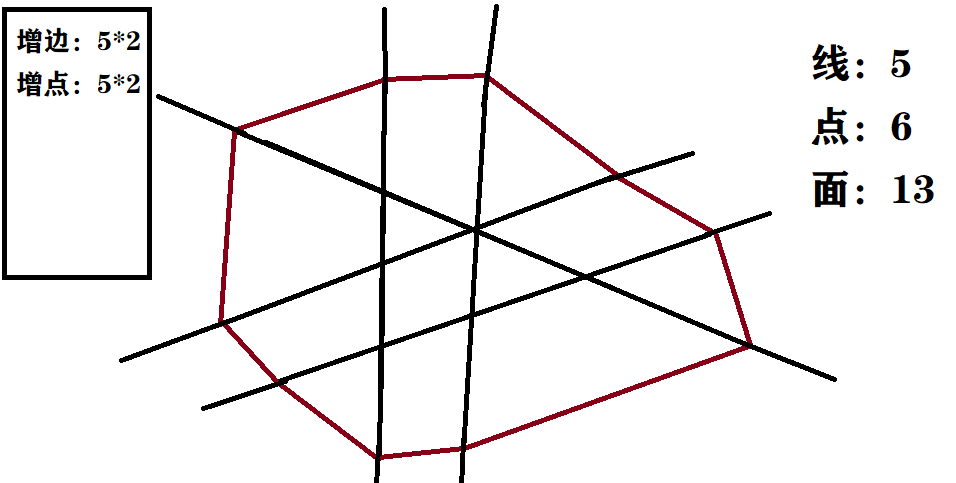
棕色的線是增加在面內(nèi)的線,和外圍面的數(shù)量相同
接下來,我們可以把它想象成一個立體的,每一個線段作為一條棱,棕色線的作為底邊的立體形狀。這樣
它就有28條棱,16個點,根據(jù)歐拉公式V+F-E=2我們可以得出(面數(shù) = 棱數(shù) - 點數(shù) +2),也就是這里的28-16+2=14個面
去掉底面剛好就是13,是原圖形的答案。
首先棱數(shù) 28 = 底邊(原線數(shù)*2=10)+原線數(shù)(5)+點截線產(chǎn)生的新棱數(shù)(原點數(shù)*2+計算時重復的點的個數(shù)*1)
點數(shù)16 = 底邊的點(原線數(shù)*2=10)+原點數(shù)(6)
注 :兩個線相交他們互相切割形成兩條新的線(也就是這里的棱),圖中因為有三線共點,所以計算時重復的點只截了新加入的線,所以只加了一條棱。
綜上所述,我們算得的平面狀態(tài)面的數(shù)量為: 線數(shù) + 點數(shù)+重復的點數(shù)+1。(地面點數(shù)和邊數(shù)相同直接消掉了,去掉底面-1)
在這里 5 + 6 +1 +1 =13。另外這題可以用set集合去對輸入輸出和重復點去重。
代碼如下:
#include <bits/stdc++.h> #include <stdlib.h> #include <set> #include <algorithm> using namespace std; set<pair<int ,int> > lines; set<pair<double ,double> > points; int n,m=0,num[1005]; int k,d; int main() { ios::sync_with_stdio(false),cin.tie(0),cout.tie(0); cin>>n; for(int i=0; i<n; i++) { cin>>k>>d; lines.insert({k,d}); } for(set<pair<int,int> >::iterator l1=lines.begin(); l1!=lines.end(); l1++) { set<pair<double,double> > hasCut; for(set<pair<int,int> >::iterator l2=--lines.end(); l2!=l1; l2--) { if(l1->first-l2->first!=0) {//分母不為0 double x=(l1->second -l2->second)/(double)(l2->first- l1->first); double y= (l1->first)*x+l1->second; //對點集判斷,已經(jīng)出現(xiàn)才算重復,而且一條線不能被同一個點截兩次 if(points.find({x,y})!=points.end() && hasCut.find({x,y}) == hasCut.end()) m++; points.insert({x,y}); hasCut.insert({x,y}); } } } cout<<lines.size()+points.size()+m+1<<endl; return 0; }
除了find函數(shù)其實還可以用count,因為集合相同元素只能有1個所以count只有0和1。

 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號