模擬賽總結（三）

糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖糖

2024.9.16

~~重新定義飲料為一大杯冰沙~~

~~胃：這把生死局（指抿一口就開始起反應...）~~

~~早上就不停反嘔，下午整這一出真是笑嘻了~~

T1 不相鄰集合

以為貪心假的，結果對了

就是對新加的數看看有沒有左鄰右舍被取過，沒有就計入答案

code

T2 線段樹

暴力\(20\)

考慮到線段樹開點方式，點編號之和肯定可以寫成一次函數，具體的，設\(f_{n,x}\)表示根為\(x\)，有\(n\)個葉子是的和，那么\(f_{n,x} = k_n \times x + b_n\)

然后有關系

\[f_{n,x} = f_{\lceil \frac{n}{2}\rceil,2x} + f_{\lfloor \frac{n}{2} \rfloor,2x + 1} + x \]

代入表達式可得：

\[\begin{cases} k_n = 2(k_{\lfloor \frac{n}{2} \rfloor} + k_{\lceil \frac{n}{2}\rceil}) + 1 \\ b_n = b_{\lfloor \frac{n}{2} \rfloor} + b_{\lceil \frac{n}{2}\rceil} + k_{\lfloor \frac{n}{2} \rfloor} \end{cases}\]

可以記憶化處理

然后正常跑查詢，如果找到\([l,r]\)在詢問區間內，貢獻就是\(k_{r - l + 1} \times id + b_{r - l + 1}\)

~~byd mid沒開ll耗掉不少時間，被#define int long long教育力~~

code

T4 園藝

聽說數據很水最多枚舉兩個拐點可過..

正解鞋油+單隊，感覺和之前掉餡餅的題很像

std1
std2

2024.9.22

菜死了

T1 自然數

下洗了，不會

先求出\([1,i]\)的mex，記為\(mex_i\)，這個數組單調不降。然后記錄\(a_i\)在后面第一次出現的位置\(nxt_i\)

接下來枚舉左端點，每次移動都為刪掉一個\(x = a_l\)，然后\(mex\)中大于\(x\)的值就會被改成\(x\)，修改區間右端點就是\(nxt_l - 1\)，左端點需要二分找第一個大于\(x\)的點，可以通過記錄最大值實現

然后上線段樹做區間修改，區間最值，區間求和即可

code

T2 錢倉

~~手膜膜錯辣~~

改過來后發現就是貪心，然后存在這樣一個點：該點后面的點的貨物不會運到該點前面

這個點滿足是最大子段和的起點（意思就是有足夠多的貨補給后面），由此處破環成鏈貪心即可

code

T3 游戲

考場上拿無窮近似推了個賊像的式子，然而還是遺憾離場

std

code

T4 暴雨

暴力搜索\(20\)

正解大炮，？？？

2024.9.28

T1 一般圖最小匹配

貪心可以有\(75\)，但是考場上\(RE\)了一半多，后來使用魔法常數就\(OK\)了

damn

整潔大炮

先對\(a\)【排序，這樣后取相鄰的一定最優

定義\(dp_{i,j,0/1}\)表示到第\(i\)個數匹配了\(j\)對，并且第\(i\)個數沒有用上

則

\[\begin{cases} dp_{i,j,0} = min(dp_{i - 1,j,0,},dp_{i - 1,j,1})\\ dp_{i,j,1} = dp_{i - 1,j - 1,0} + a_i - a_{i - 1} \end{cases} \]

使用滾動優化

code

T2 重定向

暴力枚舉刪除位+填數有一半分

考慮到字典序最小，使用貪心

設\(minnum\)表示最小的未填數，\(minn_i\)表示\(a_i \sim a_n\)中最小的數

\(a_i = 0\)

如果minn_i < minnum，就要把\(minn_i\)刪掉往這里放
\(a_i \neq 0\)
- \(a_i > a_{i + 1}\)，則刪掉\(a_i\)更優
- \(a_{i + 1} = 0\)，如果\(a_i > minnum\)，那么刪掉\(a_i\)更優

可以用優先隊列維護要填的數

注：在初始化優先隊列中，循環上界為\(n\)時會\(RE\)，要改為\(n + 1\)（~~不知道為甚莫~~）

code

T3 斯坦納樹

戳

T4 直徑

再戳

2024.10.2

障保齡而東之，回暴力于既倒

T2 肥胖

忘了可以從\(1\)走到其他點開吃，直接成\(10\)分，還都是\(-1\)...

為了成功，肯定想要把限制放大點

于是可以建最大生成樹

然后考慮選擇的邊中最小的，設為\((u,v,w)\)，此時有一個結論：先吃完一個子樹再去吃另一個不劣于反復橫跳

證明的話，考慮反復橫跳吃的某一步肯定是吃了一棵子樹的最后一個然后跳到另一個，此時經過\((u,v,w)\)時的寬既有一棵子樹的所有糖還有另一棵子樹的一些糖，那還不如全吃完一棵，然后只經過一次\((u,v,w)\)到另一棵樹里吃吃吃

然后考慮答案，設\(sum_u\)表示\(u\)字數內糖果總和，\(ans_u\)表示吃完\(u\)為根的子樹的最大初始體寬

假設從以\(u\)為根到以\(v\)為根，此時一個是要保證能過邊，即\(w \geqslant sum_u\)，一個是要能吃完\(v\)樹，就是\(ans_v \geqslant sum_u\)，兩答案取\(\min\)，反之同理，\(u,v\)互換即可，最后兩個\(min\)取個\(max\)即可

注：由于一開始\(ans_i\)未求出，所以初始化成極大值

code

T3 分攤

看到分數嚇似了

實際上大概是這樣：只有兒子全滿了自己才開始存錢

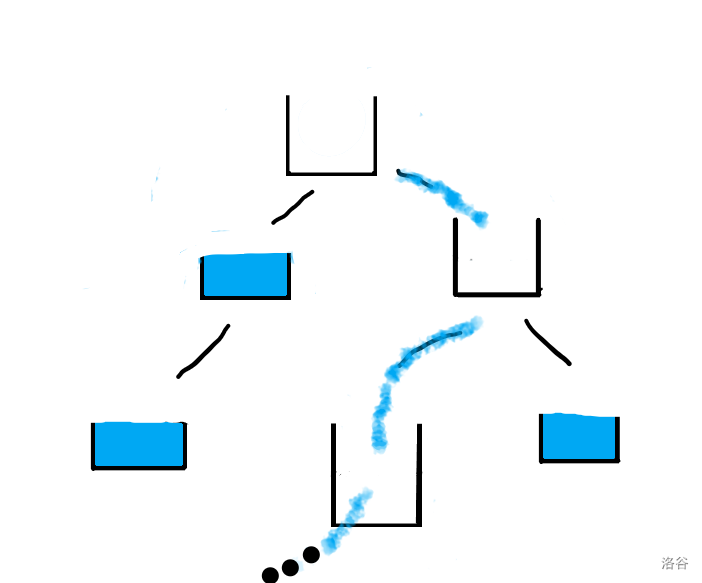
設\(v\)為與當前點\(u\)有同樣父親的兄弟節點，那么父親至少有\(x + \sum \min(sum_v,x)\)塊錢才能保證\(u\)拿到\(x\)塊錢,其中\(sum_v\)是\(v\)的子樹和

然后打\(log\)的話考慮倍增，但是略有不同

考慮到增量的維護，由于每一層都要和\(x\)比大小來產生貢獻，所以一口氣跳太多的話增量可能不能統一計算，會很麻煩

考慮一次跳躍，當上面的\(\min\)等于\(x\)時\(x\)會翻倍，此時可能計算方式不同，那么到這個點之前的路徑的計算方式一樣，那么另設一個\(g_{u,i}\)表示當\(u\)跳\(2^i\)級時，\(x \leqslant g_{u,i}\)時計算方式一樣，\(g\)可以在維護增量的時候一并求得

那么就可以統一計算：二分\(\min\)的分界點，左邊計入子樹和，右邊計入若干個\(x\)

code + 注釋

T4 修路

暴力有\(27\)分

暴力時發現交點在圓內當且僅當兩個由端點形成的區間嚴格相交（不取等）

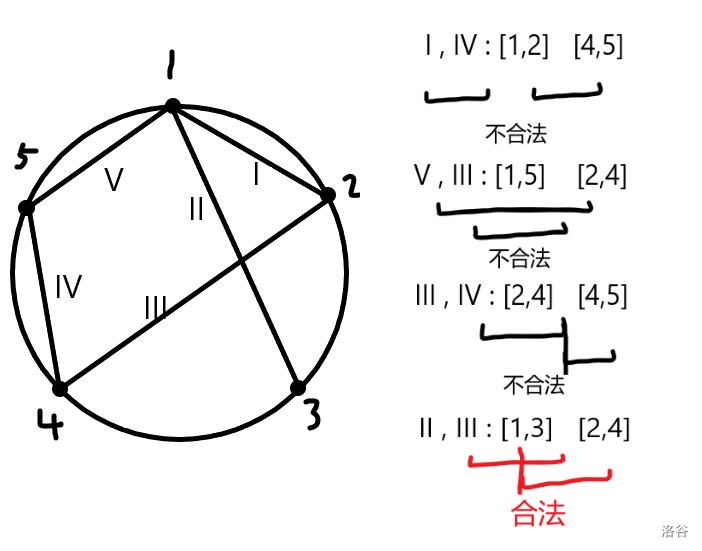
由此可以維護區間，打log可以使用線段樹一類物質

詳情

code

T1 戰爭

口胡可得\(31\)

std

2024.10.3

~~親手殺死整潔~~

T2 尋寶

看到傳送門單向直接ban掉并查集，事后發現可以在并查集上建單向邊跑暴力，畢竟最多\(100\)條邊...

code

T1 構造字符串

手玩出\(30\)

正解就是相同的合并成塊，然后\((x_i + z_i,y_i + z_i)\)這兩處一定不同，連邊，非法就是塊內有邊

然后填數，塊內有位置填了直接染掉即可，否則求\(mex\)即可

code

T3 序列

官方題解：

容易發現這是一個與斜率有關的題目，這種題目通常通過維護凸包，或者李超樹維護
跨過\(p_i\)的區間容易轉化為：以\(p_i\)為右端點的最優+以\(p_{i}+1\)為左端點的最優
兩個問題同理，以右端點（\(p_i\)）為例
設\(sa_i=\sum_{j=1}^i a_j\)，\(sb_i=\sum_{j=1}^ib_j\)
最優即\(\max_{1\leq l\leq r}\{(sa_{r}-sa_{l-1})-k(sb_{r}-sb_{l-1})\}\)
即\(sa_r-k\cdot sb_{r} +\max_{0\leq l<r}\{ksb_{l}-sa_l\}\)，離線之后李超樹維護直線即可
時間復雜度為\(O(n\log n)\)，常數略大，空間復雜度為\(O(n)\)

往李超上套，就是把\(k\)當成\(x\)軸去搞

附李超講解

附李超板題

70分流產代碼

T4 構樹

gugugugugugu~

2024.10.4

人死了一白天晚上才緩過來

T1 玩游戲

貪心寫假了

不能只看挪動一位下左右誰最優，可能當前并入一個相對較大的數但是可以再并一個很小的負數，所以要用前綴和分別把左右指針推到極小處，考慮到極小處不一定是端點，所以要反著從端點往極小處跑，同樣用前綴和實現

code

T2 排列

std

code

T3 最短路

std太吊

將返回等價為建反邊后的前往，然后用dijkstra分別推進兩個支路，使用bitset助力維護

設\(dis_{x,y}\)表示從\(1\)走正邊到\(x\)，走反邊到\(y\)（從\(y\)返回\(1\)）的答案

code

T4 矩形

矩形重疊想到掃描線，但不會寫

std

code

2024.10.5

T1 送花

從左往右掃，貢獻是\([1 / lst_i + 1,i]\)，然后掃到重復顏色時要刪貢獻，考慮到每次從\(1\)開始刪會重復，所以刪除區間是\([1 / lst_{lst_i},lst_i]\)

code

T2 星空

\(n \leqslant 300\)起手\(Floyd\)有\(45\)

考慮轉換坐標系

將原坐標系順時針旋轉\(45\)度，那么原來的坐標\((x,y)\)就會變成\((x - y,x + y)\)，設為\((x',y')\)接著發現原坐標系中的距離變成了\(\min(|\Delta x'|,|\Delta y'|)\)，那么距離為\(0\)的點就是\(x'\)或\(y'\)相同的點，使用并查集合并

最小距離的話就分別按\(x',y'\)排序，在\(x'/y'\)變化處作差比較并記錄所在塊的編號，那么個數就是記錄的每對塊的\(size\)乘積的和，注意去重

code

T3 零一串

吊炸天

std

code

T4 Revive

線段樹 + \(dfn\) + 樹狀數組...

std

2024.10.6

虛死了

不太想寫東西，扔\(std\)得了

std1

std2

2024.10.7

~~題目標題說得對~~

T1莓良心

糖，以為\(\mathfrak{Segment-Tree}\),把絕對值拆成\(max,min\)...

若干個區間相交的標志：\(maxl <= minr\)，此時所有數字沒貢獻

對于剩余未相交區間，在\([minr,maxl]\)中間取數最優，此時所有數字貢獻為\(maxl - minr\)，乘上區間數目

每次更新\(maxl,minr\)都會少兩個區間，求貢獻時還要算上他自己

code

T3 團不過

正難則反

設\(f_i\)表示有\(i\)堆石子時的非法數量，\(g_i\)表示總數

\(g_i\)很好求，就是全排列：\(g_i = A_{2^n-1}\)

考慮求\(f_i\)

既然要讓異或和為\(0\)，那么不妨直接讓第\(i\)堆石子數等于前\(i - 1\)堆石子數的異或和，此時要求前\(i - 1\)堆異或和不為\(0\)，有\(g_{i - 1} - f_{i - 1}\)種，然后考慮重復的情況，第\(i\)堆和前面某一堆重復，那么剩下的\(i - 2\)堆異或和就是\(0\)，一共有\(i - 1\)堆，重復值的個數為\(2^n - 1 - (i - 2)\)（重復的兩堆和剩下的要互異），所以減去\((i - 1) \times f_{i - 2} \times (2^n - i + 1)\)

答案：\(g_n - f_n\)

T2 盡梨了

枚舉\(b\)中\(1\)的個數，設為\(c\)，設當前行\(1\)的個數為\(k\)

\(k < c\) : 有一些\(b\)的位置是\(1\)，而矩陣中是\(0\)，那么\(a\)對應位置就要放\(0\)
\(k > c\) : 同理，\(a\)只能放\(1\)
\(k = c\) : 此時\(b\)可以全部接住\(1\)，\(a\)可以隨便選

考慮計算

注意到\(k = c\)時要求所有\(k = c\)的行相同，判定稍后說，此時\(b\)唯一確定，所以方案數是\(2^{num}\)

如果不存在\(k = c\)的行，那么\(b\)不確定，此時需要求出\(k < c\)至少需要多少個\(1\)，以及\(k > c\)中至少需要多少個\(0\)，后者可以求出至多有多少個\(1\)，至多與至少的差是備選位置數量，然后可以選的有\(c - minn\)種，是個組合數

二者相互獨立

接下來考慮判定合法，考慮到\(b\)要接住所有\(k <= c\)的行的\(1\)和\(k >= c\)的\(0\)，所以可以求并，那么前后夾擊一下，\(pre\)求\(1\)的并，\(nxt\)求\(0\)的并，根據第二種情況可得，在\(c\)相同時，\(nxt\)為1的為\(pre\)必須為\(1\)而且\(nxt\)的\(1\)數量 \(\geqslant\) \(pre\)的\(1\)數量，由此判斷

code

T4 七負我

特殊性質（菊花圖）提示我們均分最優，實際上確實如此，證明可以看看，接著就是求最大團，可以使用\(BK\)，就是一個搜索

code

2024.10.8

簡單考了一場~~以替換月考~~

T1 哈希結果空間小了 T2 Tarjan忘了 T3 貪心假了...

放個鏈接

2024.10.13

都想到一點但不多

T1 Hunter

其實很簡單，想復雜了

只有其他獵人在\(1\)號獵人之前死掉才會有\(1\)發的貢獻，而根據成正比可得獵人\(i\)在\(1\)前面死的概率為\(\frac{w_i}{w_i + w_1}\)，累加即可

code

T2 Defence

一眼看出是最長連續\(0\)的長度，但是暴力都炸了

有坑：如\(00100\)，需要\(4\)次，所以還有情況就是左右兩端連續最長\(0\)的和

使用線段樹合并，維護區間最大\(0\),左右端最多\(0\),在區間銜接處分討處理端點\(0\)的數量，因為可能出現整個區間全是\(0\)的情況

code

T3 Connect

一眼最大生成樹然后加回去一部分刪的邊，但是不好維護，因為可能加著加著就把兒子連起來成新路徑了

后來想到給\(1 \to n\)的“主鏈”上加東西，但是被題目搞懵了一下就下考了（輸出給的是刪掉邊和最小，但題目說的是剩余邊最大和，我直接****）

使用狀壓，預處理出所有能往主鏈上掛的東西\(sum_S\)，然后處理銜接邊\(cj_{S,i}\)，之所以分開是因為掛的東西一點不在主鏈上，但是銜接的有一端在主鏈上，有一端在掛件里。（\(S\)是點集，\(i\)是在主鏈上的一點）

然后\(dp\)的時候一邊延長主鏈一邊掛東西就行了

code

2024.10.14

byd被wx和hl雙重問候

T1score and rank

思路比較接近std，想到用堆維護

解釋：遇到負數就把他擺平，如果當前總和小于負數絕對值就直接將總和置為\(0\)

code

T2 HZOI大作戰

一眼倍增，不會維護...

解釋：等價于重定義\(f_{u,i}\)表示從\(u\)開始進行\(2^i\)次交換后到達的點，維護方式和lca基本一致

code

T4 gtm和joke的星球

斯坦納樹板子，原理就是最終連通圖必定是個樹，使用狀壓進行兩種操作：

1.合并：將有相同根的點集合并

2.換根：使用最短路更新點集的根使得邊權和盡可能的小

對每個點先進行第一步，再對整個點集進行第二步

code

T3 Delov的旅行

只能意會..

code

2024.10.15

T1 限速（speed）

比較簡單，建出最小生成樹，如果樹內最大邊大于\(k\)，直接統計答案，否則枚舉剩下的邊找更優的替換

code

T2 酒鬼（drunkard）

把題審成部分分了，就只有部分分了(\(27pts\))

使用set維護，因為線索相互影響，要按時間排序再搞

發現\(p_i = 1\)時非常麻煩：擁有同一個\(min\)的\(p_i=1\)的時間滿足奇偶性相同，比如時刻為\(1,3,5,7\)的\(min\)都是\(1\)，所以如果插入不同奇偶性時刻\(t'\)，比如\(t = 4\)時在\(1\)，那么\(min\)會變成\(5\)，因為單看\(4\)，它的\(min\)是\(0\)，不符合\(1,3\)，但是還可以不走，所以\(min\)是\(5\)，因此再用一個\(set\)單獨維護\(p_i = 1\)的時刻用于更新\(min\)。但還有一種情況：插入\(100\)的話\(min\)會變成\(7 + 1 = 8\)，所以還要分類：如果\(t'\)大于最大，新的\(min\)就是最大值加一，否則就是\(t' + 1\)，后者還要把比\(t' + 1\)小的值刪掉

但是還有一些線索會影響\(minn\)的奇偶性：時間上距離\(min\)最近的點。還是上面的\(1,3,5,7\)，插入\(10,3\)，會發現\(min\)不能是\(1\)了，但\(min = 8\)可以，所以還要改。而且最近點也要更新，一旦更新就還要去維護\(p_i = 1\)的時刻...

其他線索的維護就比較簡單:插入\(set\)后找前驅后繼，滿足以下兩點即可：

\(|\Delta T| >= dis\)
\(|\Delta T| - dis = 2k\)

后一條在判斷時間上距離\(min\)最近的點時也用到了

再加上特判有沒有前驅后繼等亂七八糟的細節 ~~以及調試~~，長度來到驚人的\(3k\)

code

T3 距離（distance）

亂搞\(40\)

枚舉點對，形成的貢獻作用范圍是\(1 - lca\)的鏈，樹剖+線段樹維護即可有\(70\)

差點沒T2std長.....

T4 團隊選拔（selection）

2024.8.6 T4原題戰績可查

2024.10.16

糖死了把文件工工整整放到\(D\)盤忘交了...

T1 第一題

睡了導致什么也沒有寫...

只要占領全部葉子，其他點就占完了，所以考慮怎么占完葉子

占領一個葉子節點要么從其他葉子轉移，要么從根新派一個兵，對于前者事先按照深度排序，然后對于每個葉子決策兩種方式計算

code

T2 第二題

二分答案，然后遍歷所有點把差抹平到二分值以下，計算所需代價是否超過\(K\)，\(40\)分抹一遍即可，要獲得\(90\)多分要抹十遍以上，最高\(95\)

考慮換一種方式：建圖遍歷，用類似\(Dij\)的方式搞，優化方案是先對所有點按權值排序（方式同\(dij\)），然后利用特殊性質用兩個隊列模擬\(Dij\)砍掉優先隊列的\(log\)，執行一遍即可

code

T3 第三題

數位\(dp\)，定義\(dp_{i,j,0/1,0/1}\)表示前\(i\)位一共有\(j\)個\(1\)，卡/不卡下界(L)，卡/不卡上界(R)

利用\(pair\)，\(first\)存排名，\(second\)存和。考慮到只要有一位不卡上界后面的就都一定不卡，所以要按位與

考慮怎么判斷卡不卡界限（由于對區間所有數排序所以初始狀態下一定卡）

對于上界，當前在第\(i\)位，如果這一位是\(0\)，那沒辦法，因為前面一直卡著，選\(1\)的話就大于上界了，卡的狀態為\(1\)。相反，如果是\(1\)，就有了不卡的機會，狀態為\(0\)，發現剛好是異或的關系。下界剛好與上界相反，不用異或

更多細節看代碼

code

T4 第四題

大炮

大腎tj

code

2024.10.17

T1 傳送 (teleport)

分別按照\(x,y\)排序，每次排完序后給相鄰邊連邊，最后跑最短路即可

code

T2 排列 (permutation)

考慮到最多只有\(10\)的數可能會使得\(\gcd\)為\(k\)，稱為關鍵數，不妨狀壓這十個數的狀態進行大炮

設\(dp_{i,s,j}\)表示當前放到第\(i\)位，關鍵數出現狀態為\(s\)，最后一位放的是第\(j\)個關鍵數，\(0\)表示不放

枚舉最后一位放什么即可，如果上一位和這一位都是關鍵數則需要檢查\(\gcd\)，其他情況直接轉移即可

code

T3 戰場模擬器 (simulator)

大數據結構模擬題

對于護甲和死亡，分類討論，如果當前區間有護甲/死亡人數就要遞歸到葉子，否則就是普通的區間修改，需要寫兩個函數，\(kill\)專門遞歸到葉子，\(attack\)/就只是普通修改，然后每次分左右區間都要分討一下來決定調用什么函數，以此減小復雜度

code

T4 點亮 (light)

60ptscode

2024.10.19

暴力不掛好心情~

由于是后期補的，沒太多時間寫，所以扔篇大題解

戳

T1 排列最小生成樹

暴力\(50\)，正解使用根號分治，每個點只需要建\(\sqrt n\)條邊

T2 卡牌游戲 (cardgame)

把\(A\)摞到\(B\)上面發現 \(j \equiv i \pmod g\),\(g = \gcd(n,m)\)的\(B_j\)都會和\(A_i\)對對碰，所以分別存儲，二分找界限統計長度即可

code

T3 比特跳躍 (jump)

就按照題解說的模擬就行了

\(69pts\),按位或的包沒過

T4 區間 (interval)

咕咕咕

2024.10.20

T1 Reverse

發現每次交換\(1\)可達的位置奇偶性相同，所以使用\(set\)分別存儲奇偶數，每次\(lowerbound\)找下限可達點，然后用\(bfs\)跳，并刪去被更新的點，這樣就能保證每個點只被更新一次。注意迭代器的尿性

code

T2 Silhouette

先對\(A,B\)排序，并不影響答案，然后令每一格 \(s = \min(A_i,B_j)\)，發現相同\(s\)的個子形成矩形或者\(L\)型，使用容斥計算，具體原理戳

code

T3 Seat

一個結論是，對于任意一個人，他坐下時離最近的人的距離是一定的，那么可以將所有人按照坐下時的距離分成若干層。對于距離為\(1\)的人特殊處理，因為此時怎么選都是等概率的，對于其他距離的人，他們選擇座位時可能會存在長度為奇數的空區間以及長度為偶數的空區間，前者有一個備選位置，后者有兩個，所以需要大炮。定義\(dp_{i,j}\)表示已經坐了\(i\)個人，還剩\(j\)個偶區間的概率，根據當前人坐在奇區間內還是偶區間內來轉移

考慮到偶區間存在兩個備選位置，兩個位置是等價的，因此欽定一個人坐在某個位置，得到一系列答案，再對稱推出選另一個位置的答案即可

code

T4 萬豬拱塔

咕咕咕

2024.10.21

~~看到大家都不會做就放心了~~

~~T2沒判誤解掛了\(20\) QwQ~~

T1 島嶼

怎么說呢。。。

code

T2 最短路

考慮建立最短路樹，以1為根節點。

如果把點\(i\)到它父親的邊斷了,為了到達，我們需要一條邊連接\(i\)的子樹內任意一節點和子樹外任意一節點

這樣需要枚舉非樹邊，為了減少時間復雜度，不妨考慮一條非樹邊的貢獻

如圖，對于非樹邊\((u,v)\)，可以轉化為\(dep_u + dep_v + w(u,v) - dep_k\)，前三者都是定的，只有后者動，所以跳祖先更新\(ans\)，可以使用并查集優化 ~~但這題暴力跳父親也能過~~

code

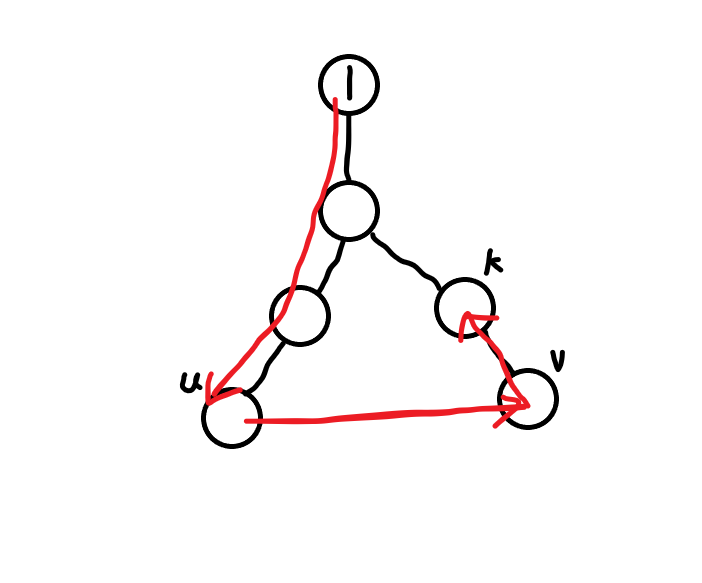
T3 列表

第一個性質可以導出第二個性質

定義雙指針 \(L,R\) 為出現的連續數字（即\(L,L + 1 ... R\)在\(S\)內出現），然后用性質2單調移動指針

根據性質2的等價轉換（區間內至少有\(R - L + 1 - (n - i)\)個數）,可得\(num \geqslant R - L + 1 - (n - i)\)

這里有個巧妙的轉化：對于一個位置，枚舉到它時的\(i\)是一定的，所以一個位置的\(n - i\)是固定的，可以建樹時設好。那么移動指針的時候維護\(num\)即可，比如\(R\)右移一位，然后\(R\)的貢獻就是給\([1,pos_R]\) + 1，這個區間是\(pos_R < N + 1\)的區間，\(> N + 1\)時應該是\([pos_R,2N + 1]\)，但是\([N + 1 - i,N + 1 + i]\)是對稱的，又因為一個數最多產生一個貢獻，所以區間折疊，這樣不管\(L,R\)怎么變修改區間都是\([1,pos]\)

那么每跳一次\(R\)，用非法情況跳\(L\)，即存在一個位置的值不滿足大于等于的關系，那么如果最小值都滿足就合法了

code

T4 種植

對偶圖的意思就是說新建一個圖（此題中新圖似乎還不是對偶圖，那玩意兒是最小割用的，這里只是單純沿用定義），新圖的邊與舊圖的邊恰好有一個交點，對應題目中的每條路徑上恰好一株農作物

\(35pts\)的數據告訴我們，沒障礙時左下到右上的對角線條數就是答案。我們可以由此擴展，建出由該方向對角線組成的圖，就是所謂的對偶圖，然后用這個圖求答案。此題中的性質就是新圖中左下角到右上角的路徑數就是答案

考慮怎么處理障礙物。對角線肯定是沿著空地延伸的，當遇到障礙時，需要跳到障礙旁邊的空地以繼續延伸，所以將障礙周圍的三個格子合并入他自己，就是所謂的四聯通塊縮點，然后直接對縮的點和空地連邊即可

求路徑數用拓撲序就行了

code

2024.10.22

簡單簽到+暴力亂c

T1 冒泡排序

就是對 \(mod\) \(k\)同余的排序了，分組排序再輸出即可

code

T2 染色

暴力完全寫不出來

就是把整個區間分成若干個色段，分成\(i\)個色段有\(f_i\)種方法，這\(i\)個色段的分布有\(C_{n - 1}^{i - 1}\)種

\(bitset\)優化：用異或模擬減去\(dp_c\)，然后右移，因為多加了一個字符，最后或一個\(2\)模擬加一

code

T4 山巒（mountain）

數據范圍注定這題很暴力，搜索都有\(35\)

考慮到一行填數方案最多\(46280\) （首項為\(10\)），所以直接把所有可能的填數狀態搜出來，用\(hash\)壓縮并賦予編號

設\(dp_{i,S,w}\)表示第\(i\)行填數方案為\(S\)，總和為\(w\)的方案數

原始的方法是枚舉相鄰行\(check\)后轉移，優化是按照\(S\)的字典序做前綴和，這里的前綴和分為兩步：首先找到上一行狀態的后繼\(S'\)，將\(dp\)匯入。其次是行內前綴和，因為行內遞減也有答案的累積，所以還要預處理首項相同時各方案的前綴關系以進行前綴和

更多細節見代碼,第\(18\)個點卡常，一堆人上火車頭干過去的...

T3 圖

標程\(23k\)..............古神題............

感受一下威壓

#include <cstdio>
#include <map>
#include <iostream>
#include <algorithm>
#include <bitset>
#include <queue>
#include <stack>
#include <vector>
#include <random>
#include <cstring>
#include <ctime>
#include <cmath>
#include <assert.h>
#include <unordered_map>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace __gnu_pbds;
using namespace std;
#define LL long long
#define pp pair<LL, LL>
#define mp make_pair
#define ull unsigned long long
namespace IO {
const int sz = 1 << 22;
char a[sz + 5], b[sz + 5], *p1 = a, *p2 = a, *t = b, p[105];
inline char gc() {
    //	return p1==p2?(p2=(p1=a)+fread(a,1,sz,stdin),p1==p2?EOF:*p1++):*p1++;
    return getchar();
}
template <class T>
void gi(T& x) {
    x = 0;
    int f = 1;
    char c = gc();
    if (c == '-')
        f = -1;
    for (; c < '0' || c > '9'; c = gc())
        if (c == '-')
            f = -1;
    for (; c >= '0' && c <= '9'; c = gc()) x = x * 10 + (c - '0');
    x = x * f;
}
inline void flush() { fwrite(b, 1, t - b, stdout), t = b; }
inline void pc(char x) {
    *t++ = x;
    if (t - b == sz)
        flush();
}
template <class T>
void pi(T x, char c = '\n') {
    if (x < 0)
        pc('-'), x = -x;
    if (x == 0)
        pc('0');
    int t = 0;
    for (; x; x /= 10) p[++t] = x % 10 + '0';
    for (; t; --t) pc(p[t]);
    pc(c);
}
struct F {
    ~F() { flush(); }
} f;
}  // namespace IO
using IO::gi;
using IO::pc;
using IO::pi;
const int mod = 1e9 + 7;
inline int add(int x, int y) { return x + y >= mod ? x + y - mod : x + y; }
inline int dec(int x, int y) { return x - y < 0 ? x - y + mod : x - y; }
inline int mul(int x, int y) { return 1ll * x * y % mod; }
inline int qkpow(int a, int b) {
    if (b < 0)
        return 0;
    int ans = 1, base = a % mod;
    while (b) {
        if (b & 1)
            ans = 1ll * ans * base % mod;
        base = 1ll * base * base % mod;
        b >>= 1;
    }
    return ans;
}
int fac[1000005], inv[1000005], Invn[600005];
inline int binom(int n, int m) {
    if (n < m || m < 0)
        return 0;
    return 1ll * fac[n] * inv[m] % mod * inv[n - m] % mod;
}
void init_C(int n) {
    fac[0] = 1;
    for (int i = 1; i <= n; i++) fac[i] = 1ll * fac[i - 1] * i % mod;
    inv[0] = 1;
    inv[n] = qkpow(fac[n], mod - 2);
    for (int i = n - 1; i >= 1; i--) inv[i] = 1ll * inv[i + 1] * (i + 1) % mod;
    Invn[0] = Invn[1] = 1;
    for (int i = 1; i <= 200000; i++) Invn[i] = (LL)(mod - mod / i) * Invn[mod % i] % mod;
}
const LL INF = 1e18;
struct node3 {
    pp mi1, mi2;
    inline void init() { mi1 = mi2 = pp(INF, 0); }
} g1[100005], g2[100005], wg1[100005], wg2[100005];
inline void Add(node3& w1, pp w2) {
    if (!w2.second)
        return;
    if (w1.mi1.second == w2.second)
        w1.mi1.first = min(w1.mi1.first, w2.first);
    else if (w1.mi2.second == w2.second) {
        w1.mi2.first = min(w1.mi2.first, w2.first);
        if (w1.mi1.first > w1.mi2.first)
            swap(w1.mi1, w1.mi2);
    } else {
        if (w2.first < w1.mi1.first)
            w1.mi2 = w1.mi1, w1.mi1 = w2;
        else if (w2.first < w1.mi2.first)
            w1.mi2 = w2;
    }
}
int Log[100005];
struct ST_min {
    node3 f[100005][21];
    inline node3 query(int l, int r) {
        node3 res;
        res.init();
        if (l > r)
            return res;
        int k = Log[r - l + 1];
        res = f[r - (1 << k) + 1][k];
        Add(res, f[l][k].mi1);
        Add(res, f[l][k].mi2);
        return res;
    }
    inline void init(int N) {
        for (int j = 1; (1 << j) <= N; j++)
            for (int i = 1; i + (1 << j) - 1 <= N; i++) {
                f[i][j] = f[i + (1 << (j - 1))][j - 1];
                Add(f[i][j], f[i][j - 1].mi1);
                Add(f[i][j], f[i][j - 1].mi2);
            }
    }
} T1[2], T2[2];
int son1[100005], son2[100005], dep11[100005], dep22[100005], seg1[100005], seg2[100005], rev11[100005],
    rev22[100005];
int top1[100005], top2[100005];
int n, fa[200005], id1[100005], id2[100005], cnt1, cnt2, dfn1[100005], dfn2[100005];
int rev1[100005], rev2[100005], f2[100005][21], sz1[100005], sz2[100005], f1[100005][21];
int st1[100005][21], st2[100005][21];
LL jp1[100005][21], jp2[100005][21];
LL dep1[100005], dep2[100005];
pp mn[200005];
struct node {
    int to, w;
};
vector<node> G1[100005], G2[100005];
inline int findSet(int u) { return fa[u] == u ? u : fa[u] = findSet(fa[u]); }
inline int Min1(int u, int v) { return dfn1[u] < dfn1[v] ? u : v; }
inline int Min2(int u, int v) { return dfn2[u] < dfn2[v] ? u : v; }
inline int LCA1(int u, int v) {
    if (u == v)
        return u;
    if ((u = dfn1[u]) > (v = dfn1[v]))
        swap(u, v);
    int k = Log[v - u++];
    return Min1(f1[u][k], f1[v - (1 << k) + 1][k]);
}
inline int LCA2(int u, int v) {
    if (u == v)
        return u;
    if ((u = dfn2[u]) > (v = dfn2[v]))
        swap(u, v);
    int k = Log[v - u++];
    return Min2(f2[u][k], f2[v - (1 << k) + 1][k]);
}
inline LL getdis(int op, int u, int v) {
    if (op == 1)
        return dep1[u] + dep1[v] - 2 * dep1[LCA1(u, v)];
    else
        return dep2[u] + dep2[v] - 2 * dep2[LCA2(u, v)];
}
inline void dfs1(int u, int ff) {
    dep11[u] = dep11[ff] + 1;
    f1[dfn1[u] = ++cnt1][0] = ff;
    rev1[cnt1] = u;
    sz1[u] = 1;
    for (int i = 1; i <= 20; i++)
        st1[u][i] = st1[st1[u][i - 1]][i - 1], jp1[u][i] = jp1[u][i - 1] + jp1[st1[u][i - 1]][i - 1];
    for (auto to : G1[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        dep1[v] = dep1[u] + w;
        st1[v][0] = u, jp1[v][0] = w;
        dfs1(v, u);
        sz1[u] += sz1[v];
        if (sz1[v] > sz1[son1[u]])
            son1[u] = v;
    }
}
inline void dfs11(int u, int ff) {
    if (son1[u]) {
        seg1[son1[u]] = ++seg1[0];
        top1[son1[u]] = top1[u];
        rev11[seg1[0]] = son1[u];
        dfs11(son1[u], u);
    }
    for (auto to : G1[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        if (!top1[v]) {
            seg1[v] = ++seg1[0];
            top1[v] = v;
            rev11[seg1[0]] = v;
            dfs11(v, u);
        }
    }
}
inline void dfs2(int u, int ff) {
    dep22[u] = dep22[ff] + 1;
    f2[dfn2[u] = ++cnt2][0] = ff;
    rev2[cnt2] = u;
    sz2[u] = 1;
    for (int i = 1; i <= 20; i++)
        st2[u][i] = st2[st2[u][i - 1]][i - 1], jp2[u][i] = jp2[u][i - 1] + jp2[st2[u][i - 1]][i - 1];
    for (auto to : G2[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        dep2[v] = dep2[u] + w;
        st2[v][0] = u, jp2[v][0] = w;
        dfs2(v, u);
        sz2[u] += sz2[v];
        if (sz2[v] > sz2[son2[u]])
            son2[u] = v;
    }
}
inline void dfs22(int u, int ff) {
    if (son2[u]) {
        seg2[son2[u]] = ++seg2[0];
        top2[son2[u]] = top2[u];
        rev22[seg2[0]] = son2[u];
        dfs22(son2[u], u);
    }
    for (auto to : G2[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        if (!top2[v]) {
            seg2[v] = ++seg2[0];
            top2[v] = v;
            rev22[seg2[0]] = v;
            dfs22(v, u);
        }
    }
}
struct node2 {
    pp u, v;
} t[400005], po1[100005], po2[100005];
LL tag[400005];
#define ls(u) u << 1
#define rs(u) u << 1 | 1
inline node2 merge(int op, node2 A, node2 B) {
    node2 tmp;
    LL res = -1;
    LL d1 =
        (A.u.first == A.v.first ? A.u.second : A.u.second + A.v.second) + getdis(op, A.u.first, A.v.first);
    LL d2 =
        (B.u.first == B.v.first ? B.u.second : B.u.second + B.v.second) + getdis(op, B.u.first, B.v.first);
    LL d3 =
        (A.u.first == B.v.first ? A.u.second : A.u.second + B.v.second) + getdis(op, A.u.first, B.v.first);
    LL d4 =
        (B.u.first == A.v.first ? B.u.second : B.u.second + A.v.second) + getdis(op, B.u.first, A.v.first);
    LL d5 =
        (A.u.first == B.u.first ? A.u.second : A.u.second + B.u.second) + getdis(op, A.u.first, B.u.first);
    LL d6 =
        (A.v.first == B.v.first ? A.v.second : A.v.second + B.v.second) + getdis(op, A.v.first, B.v.first);
    res = max(d1, d2), res = max(res, max(d3, d4)), res = max(res, max(d5, d6));
    if (d1 == res)
        tmp = node2{ A.u, A.v };
    if (d2 == res)
        tmp = node2{ B.u, B.v };
    if (d3 == res)
        tmp = node2{ A.u, B.v };
    if (d4 == res)
        tmp = node2{ B.u, A.v };
    if (d5 == res)
        tmp = node2{ A.u, B.u };
    if (d6 == res)
        tmp = node2{ A.v, B.v };
    return tmp;
}
inline void push_down(int u) {
    if (tag[u]) {
        tag[ls(u)] += tag[u];
        tag[rs(u)] += tag[u];
        t[ls(u)].u.second += tag[u];
        t[ls(u)].v.second += tag[u];
        t[rs(u)].u.second += tag[u];
        t[rs(u)].v.second += tag[u];
        tag[u] = 0;
    }
}
inline void updata(int op, int p, int l, int r, int L, int R, int w) {
    if (L > R)
        return;
    if (L <= l && r <= R) {
        tag[p] += w;
        t[p].u.second += w;
        t[p].v.second += w;
        return;
    }
    push_down(p);
    int mid = (l + r) >> 1;
    if (L <= mid)
        updata(op, ls(p), l, mid, L, R, w);
    if (mid + 1 <= R)
        updata(op, rs(p), mid + 1, r, L, R, w);
    t[p] = merge(op, t[ls(p)], t[rs(p)]);
}
inline void build(int op, int p, int l, int r) {
    tag[p] = 0;
    if (l == r) {
        if (op == 2)
            t[p].u = t[p].v = pp(rev1[l], dep1[rev1[l]]);
        else
            t[p].u = t[p].v = pp(rev2[l], dep2[rev2[l]]);
        return;
    }
    int mid = (l + r) >> 1;
    build(op, ls(p), l, mid);
    build(op, rs(p), mid + 1, r);
    t[p] = merge(op, t[ls(p)], t[rs(p)]);
}
inline void redfs1(int u, int ff) {
    po1[u] = t[1];
    for (auto to : G1[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        updata(2, 1, 1, n, dfn1[v], dfn1[v] + sz1[v] - 1, -w);
        updata(2, 1, 1, n, 1, dfn1[v] - 1, w);
        updata(2, 1, 1, n, dfn1[v] + sz1[v], n, w);
        redfs1(v, u);
        updata(2, 1, 1, n, dfn1[v], dfn1[v] + sz1[v] - 1, w);
        updata(2, 1, 1, n, 1, dfn1[v] - 1, -w);
        updata(2, 1, 1, n, dfn1[v] + sz1[v], n, -w);
    }
}
inline void redfs2(int u, int ff) {
    po2[u] = t[1];
    for (auto to : G2[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        updata(1, 1, 1, n, dfn2[v], dfn2[v] + sz2[v] - 1, -w);
        updata(1, 1, 1, n, 1, dfn2[v] - 1, w);
        updata(1, 1, 1, n, dfn2[v] + sz2[v], n, w);
        redfs2(v, u);
        updata(1, 1, 1, n, dfn2[v], dfn2[v] + sz2[v] - 1, w);
        updata(1, 1, 1, n, 1, dfn2[v] - 1, -w);
        updata(1, 1, 1, n, dfn2[v] + sz2[v], n, -w);
    }
}
inline void dfss1(int u, int ff) {
    g1[u].init();
    wg1[u].init();
    Add(g1[u], pp(0, id1[u]));
    for (auto to : G1[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        dfss1(v, u);
        Add(g1[u], pp(g1[v].mi1.first + w, g1[v].mi1.second));
        Add(g1[u], pp(g1[v].mi2.first + w, g1[v].mi2.second));
    }
}
inline void redfss1(int u, int ff) {
    node3 pre;
    pre.init();
    Add(wg1[u], pp(0, id1[u]));
    for (auto to : G1[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        Add(wg1[v], pp(wg1[u].mi1.first + w, wg1[u].mi1.second));
        Add(wg1[v], pp(wg1[u].mi2.first + w, wg1[u].mi2.second));
        Add(wg1[v], pp(pre.mi1.first + w, pre.mi1.second));
        Add(wg1[v], pp(pre.mi2.first + w, pre.mi2.second));
        Add(pre, pp(g1[v].mi1.first + w, g1[v].mi1.second));
        Add(pre, pp(g1[v].mi2.first + w, g1[v].mi2.second));
    }
    reverse(G1[u].begin(), G1[u].end());
    pre.init();
    for (auto to : G1[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        Add(wg1[v], pp(pre.mi1.first + w, pre.mi1.second));
        Add(wg1[v], pp(pre.mi2.first + w, pre.mi2.second));
        Add(pre, pp(g1[v].mi1.first + w, g1[v].mi1.second));
        Add(pre, pp(g1[v].mi2.first + w, g1[v].mi2.second));
    }
    reverse(G1[u].begin(), G1[u].end());
    for (auto to : G1[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        redfss1(v, u);
    }
}
inline void dfss2(int u, int ff) {
    g2[u].init();
    wg2[u].init();
    Add(g2[u], pp(0, id2[u]));
    for (auto to : G2[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        dfss2(v, u);
        Add(g2[u], pp(g2[v].mi1.first + w, g2[v].mi1.second));
        Add(g2[u], pp(g2[v].mi2.first + w, g2[v].mi2.second));
    }
}
inline void redfss2(int u, int ff) {
    node3 pre;
    pre.init();
    Add(wg2[u], pp(0, id2[u]));
    for (auto to : G2[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        Add(wg2[v], pp(wg2[u].mi1.first + w, wg2[u].mi1.second));
        Add(wg2[v], pp(wg2[u].mi2.first + w, wg2[u].mi2.second));
        Add(wg2[v], pp(pre.mi1.first + w, pre.mi1.second));
        Add(wg2[v], pp(pre.mi2.first + w, pre.mi2.second));
        Add(pre, pp(g2[v].mi1.first + w, g2[v].mi1.second));
        Add(pre, pp(g2[v].mi2.first + w, g2[v].mi2.second));
    }
    reverse(G2[u].begin(), G2[u].end());
    pre.init();
    for (auto to : G2[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        Add(wg2[v], pp(pre.mi1.first + w, pre.mi1.second));
        Add(wg2[v], pp(pre.mi2.first + w, pre.mi2.second));
        Add(pre, pp(g2[v].mi1.first + w, g2[v].mi1.second));
        Add(pre, pp(g2[v].mi2.first + w, g2[v].mi2.second));
    }
    reverse(G2[u].begin(), G2[u].end());
    for (auto to : G2[u]) {
        int v = to.to, w = to.w;
        if (v == ff)
            continue;
        redfss2(v, u);
    }
}
inline node3 query22(int op, int u, int v, LL ex) {
    int fu = top2[u], fv = top2[v];
    node3 res;
    res.init();
    while (fu != fv) {
        if (dep22[fu] >= dep22[fv]) {
            node3 tmp = T2[op].query(seg2[fu], seg2[u]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
            u = st2[fu][0];
        } else {
            node3 tmp = T2[op].query(seg2[fv], seg2[v]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
            v = st2[fv][0];
        }
        fu = top2[u], fv = top2[v];
    }
    if (dep22[u] > dep22[v])
        swap(u, v);
    node3 tmp = T2[op].query(seg2[u], seg2[v]);
    Add(res, tmp.mi1), Add(res, tmp.mi2);
    return node3{ pp(res.mi1.first + ex, res.mi1.second), pp(res.mi2.first + ex, res.mi2.second) };
}
inline pp query2(int u, int v, LL w1, LL w2, int c) {  //錕斤拷色錕斤拷錕斤拷錕斤拷 c
    int lca = LCA2(u, v);
    //	if(lca!=1)cerr<<lca<<" "<<"FUCK"<<endl;
    int to = u;
    LL sum = w1, tot = getdis(2, u, v) + w1 + w2;
    node3 res, tmp;
    res.init();
    LL ex = max(getdis(2, u, lca) + w1, getdis(2, v, lca) + w2);
    Add(res, pp(wg2[lca].mi1.first + ex, wg2[lca].mi1.second));
    Add(res, pp(wg2[lca].mi2.first + ex, wg2[lca].mi2.second));
    if (w1 >= tot - w1) {
        node3 tmp;
        tmp = query22(1, u, lca, w1 + dep2[u]);
        Add(res, tmp.mi1), Add(res, tmp.mi2);
    } else {
        for (int i = 20; i >= 0; i--) {
            if (sum + jp2[to][i] <= tot - sum - jp2[to][i]) {
                sum += jp2[to][i];
                to = st2[to][i];
            }
        }
        node3 tmp;
        if (dep22[to] <= dep22[lca]) {  //全錕斤拷錕斤拷 v 錕斤拷
            tmp = query22(0, u, lca, w2 + dep2[v] - 2 * dep2[lca]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
        } else {
            tmp = query22(0, u, to, w2 + dep2[v] - 2 * dep2[lca]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
            tmp = query22(1, st2[to][0], lca, w1 + dep2[u]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
        }
    }
    to = v;
    sum = w2;
    if (w2 >= tot - w2) {
        tmp = query22(1, v, lca, w2 + dep2[v]);
        Add(res, tmp.mi1), Add(res, tmp.mi2);
    } else {
        for (int i = 20; i >= 0; i--) {
            if (sum + jp2[to][i] <= tot - sum - jp2[to][i]) {
                sum += jp2[to][i];
                to = st2[to][i];
            }
        }
        if (dep22[to] <= dep22[lca]) {  //全錕斤拷錕斤拷 u 錕斤拷
            tmp = query22(0, v, lca, w1 + dep2[u] - 2 * dep2[lca]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
        } else {
            tmp = query22(0, v, to, w1 + dep2[u] - 2 * dep2[lca]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
            tmp = query22(1, st2[to][0], lca, w2 + dep2[v]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
        }
    }
    if (res.mi1.second == c)
        return res.mi2;
    return res.mi1;
}
inline node3 query11(int op, int u, int v, LL ex) {
    int fu = top1[u], fv = top1[v];
    node3 res;
    res.init();
    while (fu != fv) {
        if (dep11[fu] >= dep11[fv]) {
            node3 tmp = T1[op].query(seg1[fu], seg1[u]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
            u = st1[fu][0];
        } else {
            node3 tmp = T1[op].query(seg1[fv], seg1[v]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
            v = st1[fv][0];
        }
        fu = top1[u], fv = top1[v];
    }
    if (dep11[u] > dep11[v])
        swap(u, v);
    node3 tmp = T1[op].query(seg1[u], seg1[v]);
    Add(res, tmp.mi1), Add(res, tmp.mi2);
    return node3{ pp(res.mi1.first + ex, res.mi1.second), pp(res.mi2.first + ex, res.mi2.second) };
}
inline pp query1(int u, int v, LL w1, LL w2, int c) {  //錕斤拷色錕斤拷錕斤拷錕斤拷 c
    int lca = LCA1(u, v);
    //	if(lca!=1)cerr<<lca<<" "<<"FUCK"<<endl;
    int to = u;
    LL sum = w1, tot = getdis(1, u, v) + w1 + w2;
    node3 res, tmp;
    res.init();
    LL ex = max(getdis(1, u, lca) + w1, getdis(1, v, lca) + w2);
    Add(res, pp(wg1[lca].mi1.first + ex, wg1[lca].mi1.second));
    Add(res, pp(wg1[lca].mi2.first + ex, wg1[lca].mi2.second));
    if (w1 >= tot - w1) {
        tmp = query11(1, u, lca, w1 + dep1[u]);
        Add(res, tmp.mi1), Add(res, tmp.mi2);
    } else {
        for (int i = 20; i >= 0; i--) {
            if (sum + jp1[to][i] <= tot - sum - jp1[to][i]) {
                sum += jp1[to][i];
                to = st1[to][i];
            }
        }
        node3 tmp;
        if (dep11[to] <= dep11[lca]) {  //全錕斤拷錕斤拷 v 錕斤拷
            tmp = query11(0, u, lca, w2 + dep1[v] - 2 * dep1[lca]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
        } else {
            tmp = query11(0, u, to, w2 + dep1[v] - 2 * dep1[lca]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
            tmp = query11(1, st1[to][0], lca, w1 + dep1[u]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
        }
    }
    to = v;
    sum = w2;
    if (w2 >= tot - w2) {
        node3 tmp;
        tmp = query11(1, v, lca, w2 + dep1[v]);
        Add(res, tmp.mi1), Add(res, tmp.mi2);
    } else {
        for (int i = 20; i >= 0; i--) {
            if (sum + jp1[to][i] <= tot - sum - jp1[to][i]) {
                sum += jp1[to][i];
                to = st1[to][i];
            }
        }
        if (dep11[to] <= dep11[lca]) {  //全錕斤拷錕斤拷 u 錕斤拷
            tmp = query11(0, v, lca, w1 + dep1[u] - 2 * dep1[lca]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
        } else {
            tmp = query11(0, v, to, w1 + dep1[u] - 2 * dep1[lca]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
            tmp = query11(1, st1[to][0], lca, w2 + dep1[v]);
            Add(res, tmp.mi1), Add(res, tmp.mi2);
        }
    }
    if (res.mi1.second == c)
        return res.mi2;
    return res.mi1;
}
inline void solve() {
    for (int i = 2; i <= 100000; i++) Log[i] = Log[i >> 1] + 1;
    gi(n);
    for (int i = 1; i < n; i++) {
        int u, v, w;
        gi(u), gi(v), gi(w);
        G1[u].push_back(node{ v, w });
        G1[v].push_back(node{ u, w });
    }
    for (int i = 1; i < n; i++) {
        int u, v, w;
        gi(u), gi(v), gi(w);
        G2[u].push_back(node{ v, w });
        G2[v].push_back(node{ u, w });
    }
    seg1[0] = seg1[1] = top1[1] = rev11[1] = 1;
    seg2[0] = seg2[1] = top2[1] = rev22[1] = 1;
    dfs1(1, 0), dfs2(1, 0), dfs11(1, 0), dfs22(1, 0);
    for (int j = 1; (1 << j) <= cnt1; j++)
        for (int i = 1; i + (1 << j) - 1 <= cnt1; i++)
            f1[i][j] = Min1(f1[i][j - 1], f1[i + (1 << (j - 1))][j - 1]);
    for (int j = 1; (1 << j) <= cnt2; j++)
        for (int i = 1; i + (1 << j) - 1 <= cnt2; i++)
            f2[i][j] = Min2(f2[i][j - 1], f2[i + (1 << (j - 1))][j - 1]);
    build(2, 1, 1, n);
    redfs1(1, 0);
    build(1, 1, 1, n);
    redfs2(1, 0);
    for (int i = 1; i <= 2 * n; i++) fa[i] = i;
    int cnt = 2 * n;
    LL ans = 0;
    while (cnt > 1) {
        for (int i = 1; i <= n; i++) id1[i] = findSet(i), mn[i] = pp(INF, 0);
        for (int i = 1; i <= n; i++) id2[i] = findSet(i + n), mn[i + n] = pp(INF, 0);
        dfss1(1, 0), dfss2(1, 0);
        redfss1(1, 0), redfss2(1, 0);
        for (int i = 1; i <= n; i++) {
            int u = rev11[i], v = rev22[i];
            T1[0].f[i][0].mi1 = pp(g1[u].mi1.first + dep1[u], g1[u].mi1.second);
            T1[0].f[i][0].mi2 = pp(g1[u].mi2.first + dep1[u], g1[u].mi2.second);
            T1[1].f[i][0].mi1 = pp(g1[u].mi1.first - dep1[u], g1[u].mi1.second);
            T1[1].f[i][0].mi2 = pp(g1[u].mi2.first - dep1[u], g1[u].mi2.second);

            T2[0].f[i][0].mi1 = pp(g2[v].mi1.first + dep2[v], g2[v].mi1.second);
            T2[0].f[i][0].mi2 = pp(g2[v].mi2.first + dep2[v], g2[v].mi2.second);
            T2[1].f[i][0].mi1 = pp(g2[v].mi1.first - dep2[v], g2[v].mi1.second);
            T2[1].f[i][0].mi2 = pp(g2[v].mi2.first - dep2[v], g2[v].mi2.second);
        }
        T1[0].init(n), T2[0].init(n), T1[1].init(n), T2[1].init(n);
        for (int i = 1; i <= n; i++) {
            int u = po1[i].u.first, v = po1[i].v.first;
            LL w1 = po1[i].u.second, w2 = po1[i].v.second;
            mn[id1[i]] = min(mn[id1[i]], query2(u, v, w1, w2, id1[i]));
        }
        for (int i = 1; i <= n; i++) {
            int u = po2[i].u.first, v = po2[i].v.first;
            LL w1 = po2[i].u.second, w2 = po2[i].v.second;
            mn[id2[i]] = min(mn[id2[i]], query1(u, v, w1, w2, id2[i]));
        }
        for (int i = 1; i <= 2 * n; i++) {
            if (mn[i].second) {
                int u = i, v = mn[i].second;
                u = findSet(u), v = findSet(v);
                if (u != v) {
                    fa[v] = u;
                    ans += mn[i].first;
                    cnt--;
                }
            }
        }
        //	cerr<<cnt<<endl;
    }
    pi(ans);
}
/*
要一錕斤拷錕斤拷錕斤拷
*/
signed main() {
    freopen("graph.in", "r", stdin);
    freopen("graph.out", "w", stdout);
    srand(time(0));
    solve();
    return 0;
}
/*
 */

posted @ 2024-10-21 19:18 why?123 閱讀(31) 評論(0) 收藏舉報

刷新頁面返回頂部

蒟蒻之淚

模擬賽總結（三）

2024.9.16

T1 不相鄰集合

T2 線段樹

T4 園藝

2024.9.22

T1 自然數

T2 錢倉

T3 游戲

T4 暴雨

2024.9.28

T1 一般圖最小匹配

T2 重定向

T3 斯坦納樹

T4 直徑

2024.10.2

T2 肥胖

T3 分攤

T4 修路

T1 戰爭

2024.10.3

T2 尋寶

T1 構造字符串

T3 序列

T4 構樹

2024.10.4

T1 玩游戲

T2 排列

T3 最短路

T4 矩形

2024.10.5

T1 送花

T2 星空

T3 零一串

T4 Revive

2024.10.6

T1b

T2 競賽圖

T3 糖果

T4 樹

2024.10.7

T1莓良心

T3 團不過

T2 盡梨了

T4 七負我

2024.10.8

2024.10.13

T1 Hunter

T2 Defence

T3 Connect

2024.10.14

T1score and rank

T2 HZOI大作戰

T4 gtm和joke的星球

T3 Delov的旅行

2024.10.15

T1 限速（speed）

T2 酒鬼 （drunkard）

T3 距離（distance）

T4 團隊選拔（selection）

2024.10.16

T1 第一題

T2 第二題

T3 第三題

T4 第四題

2024.10.17

T1 傳送 (teleport)

T2 排列 (permutation)

T3 戰場模擬器 (simulator)

T4 點亮 (light)

2024.10.19

T1 排列最小生成樹

T2 卡牌游戲 (cardgame)

T3 比特跳躍 (jump)

T4 區間 (interval)

2024.10.20

T1 Reverse

T2 Silhouette

T3 Seat

T2 酒鬼（drunkard）