大炮妙妙屋
快進來,非常好玩
Od deski do deski
怎么說呢,確實想到了刪的區間互不交,然后就從放置整個區間去想,就假了
考慮修繕區間,設\(dp_{i,j,0/1}\)表示當前區間不合法/合法,在后面一位放置\(j\)種數就合法了
那就相當于有一個區間前閉后開,開的結尾有\(j\)種補全方法,就可以按照\(i + 1\)位新放的數字是\(j\)種還是剩的\(m - j\)種分討了
然后前\(i\)位最多\(i\)種,所以是\(n^2\)的
甲苯先生的字符串
矩陣裸題,遍歷\(s_1\)把相鄰的標記為不能走,用\(trick\)跑\(n - 2\)次冪,最后對矩陣求和即可
某位歌姬的故事
有熟人啊
我們發現,如果一個區間被多個限制包含,設最小限制為\(minn\),那么$ > minn$的限制不影響這個區間,所以我們考慮枚舉所有限制,然后找出所有最小限制為當前枚舉值的區間來填這個數,由此做大炮
定義\(dp_{i,j}\)表示\(i\)個區間填了當前值,最后一個填了的是\(j\),根據當前區間填不填這個值轉移即可
更多細節
#include<bits/stdc++.h>
#define ll long long
#define mod 998244353
#define N 1005
using namespace std;
int T;
ll n,q,A;
int qj[N << 1],num;
int l[N],r[N],maxx[N];
int lim[N],h[N];
int minn[N];
int len[N],pt[N];
int dp[N][N];
ll qp(ll base,ll ci)
{
ll res = 1;
while(ci)
{
if(ci & 1) res = res * base % mod;
base = base * base % mod;
ci >>= 1;
}
return res;
}
int main()
{
cin >> T;
while(T--)
{
num = 0;
memset(l,0,sizeof(l));
memset(r,0,sizeof(r));
memset(lim,0,sizeof(lim));
memset(h,0,sizeof(h));
memset(maxx,0,sizeof(maxx));
memset(qj,0,sizeof(qj));
cin >> n >> q >> A;
for(int i = 1;i <= q;i++)
{
cin >> l[i] >> r[i] >> maxx[i];
qj[++num] = l[i] - 1;qj[++num] = r[i];
}
qj[++num] = 0;qj[++num] = n;
sort(qj + 1,qj + num + 1);
num = unique(qj + 1,qj + num + 1) - qj - 1;
for(int i = 1;i <= num;i++) lim[i] = A + 1;
for(int i = 1;i <= q;i++)
{
l[i] = lower_bound(qj + 1,qj + num + 1,l[i] - 1) - qj;
r[i] = lower_bound(qj + 1,qj + num + 1,r[i]) - qj;
for(int j = l[i];j < r[i];j++) lim[j] = min(lim[j],maxx[i]);
h[i] = maxx[i];
}
int flag = 0;
for(int i = 1;i <= q;i++)//如果別的區間壓制導致某一區間取不到max就無解
{
int mx = 0;
for(int j = l[i];j < r[i];j++) mx = max(mx,lim[j]);
if(mx < maxx[i])
{
cout << 0 << endl;
flag = 1;
break;
}
}
if(flag) continue;
// cout << "M" << endl;
sort(h + 1,h + q + 1);
ll ans = 1;
for(int i = 1;i <= q;i++)
{
int pos = i;
while(pos < q && h[pos + 1] == h[i]) pos++;
memset(minn,0,sizeof(minn));
int tmp = 0;
//把與當前枚舉限制相同(lim相同)的區間提取出來
for(int j = 1;j < num;j++)
{
if(lim[j] == h[i])
{
len[++tmp] = qj[j + 1] - qj[j];
pt[tmp] = j + 1;
}
}
//在原先限制的區間為當前枚舉值的區間中,找到最小限制(lim)是當前枚舉值的部分
//由于原先區間離散化了,所以這里要映射到離散化對應的值
//這些部分是填枚舉值的部分
for(int j = 1;j <= q;j++)
{
if(maxx[j] == h[i])
{
int po = upper_bound(pt + 1,pt + tmp + 1,r[j]) - pt - 1;
minn[po] = max(minn[po],l[j] + 1);
}
}
//dp[i][j]: 填了前 i 塊,最后一個填了當前枚舉值的區間為 j
for(int j = 0;j <= tmp;j++) for(int k = 0;k <= tmp;k++) dp[j][k] = 0;
dp[0][0] = 1;
for(int r = 1;r <= tmp;r++)
{
ll tot = 0;ll sum = qp(h[i] - 1,len[r]);//剩余部分隨便填
for(int s = 0;s < r;s++)
{
if(!dp[r - 1][s]) continue;
tot = (tot + dp[r - 1][s]) % mod;
if(minn[r] > pt[s]) continue;//有交集就跳過
//不在當前塊填,那就是[1,h[i] - 1]隨便填,就是sum
dp[r][s] = (dp[r][s] + dp[r - 1][s] * sum % mod) % mod;
}
//在這里填,至少得有一個,所以減去 sum
dp[r][r] = (qp(h[i],len[r]) - sum + mod) * tot % mod;
}
ll res = 0;
for(int j = 0;j <= tmp;j++) res = (res + dp[tmp][j]) % mod;
ans = (ans * res) % mod;
i = pos;
}
for(int i = 1;i < num;i++) if(lim[i] == A + 1) ans = ans * qp(A,qj[i + 1] - qj[i]) % mod;
cout << ans << endl;
}
return 0;
}
Permutation Oddness
逆天轉化建議去看第二篇題解
潛入行動
設\(dp_{x,i,0/1,0/1}\)表示以\(x\)為根的子樹內有\(i\)個監聽器,\(x\)有沒有放,\(x\)有沒有被監聽
尤其注意的是,后兩個狀態表示\(v\)之前的合并完了,還沒有合并\(v\)的狀態
所以在式子中,等號左邊的\(dp_{x,...}\)表示已經將\(v\)并入后\(x\)的狀態,右邊的則沒有,分討的依據也是\(v\)并入后的狀態
分討見第一篇tj,就是根據后兩位共\(2 \times 2 = 4\)種情況討論
游園會
屌題
\(dp\)套\(dp\),說白了,就是記錄答案的\(dp\)有一維需要用另一個\(dp\)轉移,而不是之前的枚舉或是位運算
拿這道題來說,狀壓\(LCS\)的差分數組作為一維\(S\),這一維度轉移時需要枚舉字符做一遍\(LCS\)的\(dp\)得到\(newS\),從而實現答案的匯總與轉移
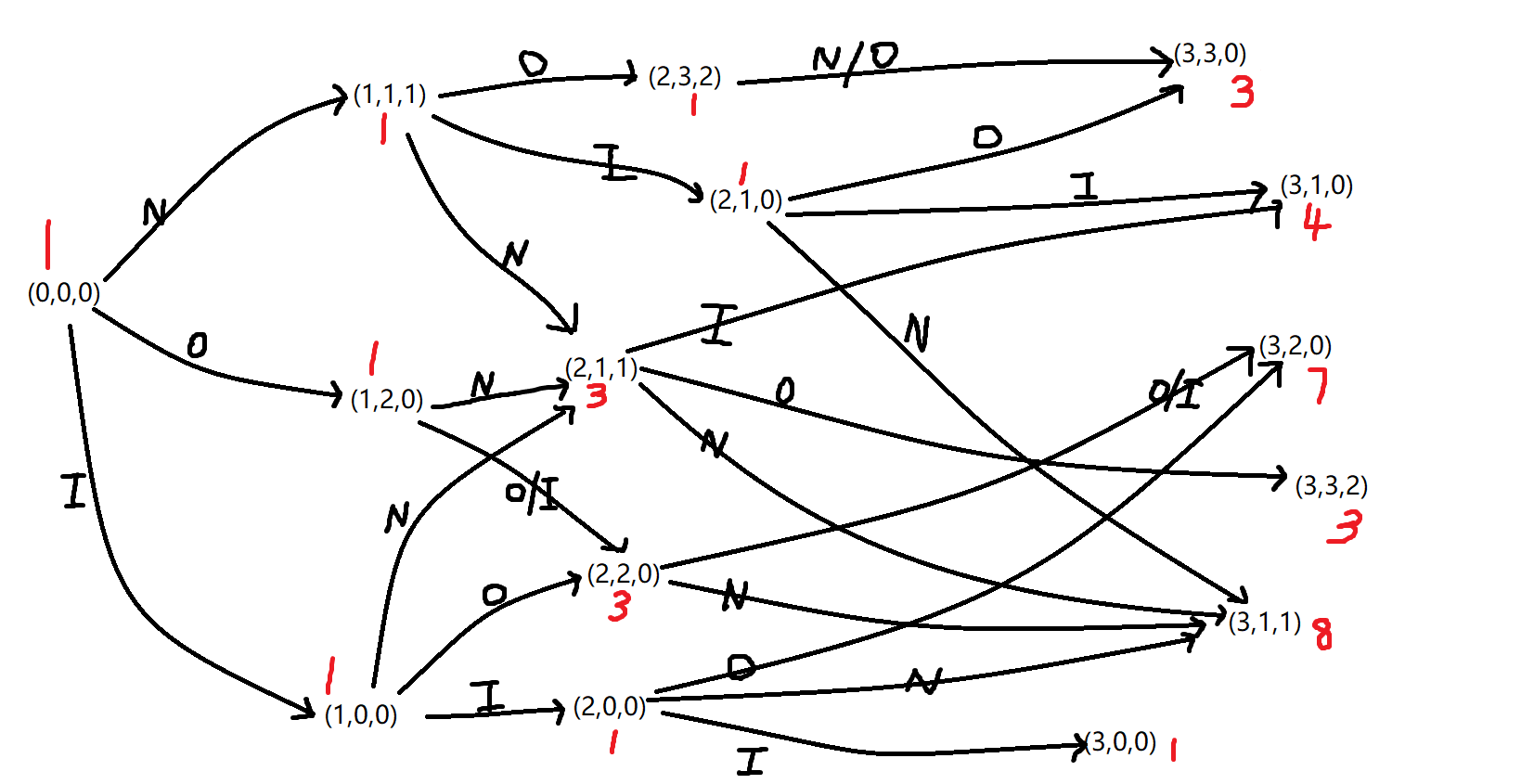
還有一種理解是用\(LCS\)的大炮搭了個自動機去跑,畫出來也很直觀(圖為樣例),每一根線都是當前枚舉字符下做一遍\(LCS\),每個括號就是一個答案\(dp\)的狀態三元組:\(dp_{i,S,0/1/2}\)表示當前在第\(i\)位,\(LCS\)差分狀態為\(S\),匹配到\(NOI\)的第\(0\)(沒配上)\(/1/2\)位。其中第三維是為了防止出現\(NOI\),來決定當前位可以放什么
Add and Remove
無語題
改刪為加,然后發現有個奇妙的東西:在兩個元素中間插入\(x\),那么\(x\)的貢獻就是兩個元素計入答案的次數之和與\(x\)的乘積
然后你發現\(a_1\)和\(a_n\)都只會被計入一次
直接一個暴搜,\(dfs(l,r,numl,numr)\),分別記錄當前區間的左右端點以及對應的計入次數,枚舉新加入的元素將原區間分成兩個子區間:\(dfs(l,p,numl,numl + numr) + dfs(p,r,numl + numr,numr)\),遞歸取min
完了


 浙公網安備 33010602011771號
浙公網安備 33010602011771號