數論+組合

注：引理見后面第四部分

1.歐拉函數，歐拉篩及應用

1.歐拉篩：

for(int i = 2;i <= N;i++)
{
	if(!vis[i]) pri[++cnt] = i;
	for(int j = 1;i * pri[j] <= N;j++)
	{
		int u = i * pri[j];
		vis[u] = 1;
		if(i % pri[j] == 0) break;
	}
}

2.歐拉函數：$\varphi(n)$

計算：$\varphi(n) = n \times \prod _ {i = 1} ^ n (1 - \frac{1}{p_i})$

用歐拉篩實現：
設 $m = pri[j] \times i$

1>若$i \bmod pri[j] == 0$

則

\[\begin{aligned} \varphi(m) &= m \times \prod _ {i = 1} ^ k(1 - \frac{1}{p_i}) \\&= pri[j] \times i \times\prod _ {i = 1} ^ k(1 - \frac{1}{p_i})\\& = pri[j] \times \varphi[i] \end{aligned} \]

2>若$i \bmod pri[j] != 0$,說明二者互質

則

\[\begin{aligned} \varphi(m) &= \varphi(pri[j]) \times \varphi(i) \\ & = (pri[j] - 1) \times \varphi(i) \end{aligned} \]

2.定理

歐拉定理：

若$\gcd(a,m) = 1$

則

\[a ^ {\varphi(m)} \equiv 1 \pmod m \]

裴蜀定理

設$a,b \in Z$

則存在$x,y$,使得

\[ax + by = \gcd(a,b) \]

推廣1：存在$x,y$,使得

\[ax + by = \gcd(a,b) \times n \]

推廣2：存在$X_1 \cdots X_n$,使得

\[\sum\limits_ {i = 1}^{n}A_iX_i = \gcd(A_1,A_2,\cdots,A_n) \]

擴展歐幾里得

對方程$ax + by = \gcd(a,b)$（設$\gcd(a,b) = d$）

可得到

\[\begin{cases} ax_0 + by_0 = \gcd(a,b)\\ bx_1 + (a \% b)y_1 = \gcd(b,a \% b) \end{cases} \]

而$\gcd(a,b) = \gcd(b,a \% b)$

則

\[ax_0 + by_0 = bx_1 + (a \%b)y_1 \]

又有$a \% b = a - (int)a / b \times b$

設$(int)a /b = k$

則

\[ax_0 + by_0 = bx_1+(a - kb)y_1 \]

整理得

\[ax_0 + by_0 = ay_1 + b(x_1 - ky_1) \]

則

\[\begin{cases} x_0 = y_1\\ y_0 = x_1 - ky_1 \end{cases} \]

這是相鄰兩組解的關系，那么這樣推下去，則$a\%b$會變成$0$(求gcd時的終止條件)

則有

\[d\times x_n + 0 \times y_n = d \]

則存在特解

\[\begin{cases} x_n = 1\\ y_n = 0 \end{cases} \]

遞歸反推每一組解即可

ll exgcd(ll a,ll b,ll &x,ll &y)
{
	if(b == 0)
	{
		x = 1;y = 0;
		return a;
	}
	ll d;
	d = exgcd(b,a % b,x,y);
	ll t = x; 
	x = y;
	y = t - a / b * y;
	return d;
}

通解：

\[\begin{cases} x = x_0 + \frac{b}{\gcd(a,b)} \times k\\ y = y_0 - \frac{a}{\gcd(a,b)} \times k \end{cases} \]

擴展歐拉定理

\[a^b \equiv \begin{cases} a^{b \operatorname{mod} \varphi(p)}----\gcd(a,p) = 1\\ a ^b-------\gcd(a,p) \neq 1,b < \varphi(p) \\ a^{b \operatorname{mod} \varphi(p) + \varphi(p)}--\gcd(a,p) \neq 1,b \geqslant \varphi(p) \end{cases} \pmod p \]

證明：

對于第一個式子，由歐拉定理

\[\begin{aligned} a^b &\equiv a^{k \times \varphi(p)+r} \\&\equiv (a^{\varphi(p)})^k + a^r \\&\equiv 1^k + a^r \\&\equiv a^{b \operatorname{mod} \varphi(p)} \end{aligned} \]

第二個式子用于$b$較小的時候

下證第三個式子

\[a = \prod\limits_{i = 1}^{s}p_i^{r_i} \]

(分解質因數)

代入

$(\prod\limits_{i = 1}^{s}p_i^{r_i})^b \equiv (\prod\limits_{i = 1}^{s}p_i ^ {r_i})^{b \operatorname{mod} \varphi(p)+\varphi(p)} \pmod p$

$\prod\limits_{i = 1}^{s}(p_i^{r_i})^b \equiv \prod\limits_{i = 1}^{s}(p_i ^ {r_i})^{b \operatorname{mod} \varphi(p)+\varphi(p)} \pmod p$

$\prod\limits_{i = 1}^{s}p_ib \equiv \prod\limits_{i = 1}^{s}p_i ^{b \operatorname{mod} \varphi(p)+\varphi(p)} \pmod p $

即證明對

\[\forall 1 \leqslant i \leqslant s,p_i^b \equiv p_i ^{b \operatorname{mod} \varphi(p)+\varphi(p)} \pmod p \]

(在此之后，模數更換為$m$

即$\forall 1 \leqslant i \leqslant s$，$p_i^b \equiv p_i ^{b \operatorname{mod} \varphi(m)+\varphi(m)} \pmod m$,并將$p_i$寫成$p$,$p$是質數)

如果$\gcd(p,m) = 1$,則

\[\begin{aligned} p^b &\equiv p^b \times 1 \\&\equiv p^{b \operatorname{mod} \varphi(m)} \times p^{\varphi(m)} \\&\equiv p^{b \operatorname{mod} \varphi(m) + \varphi(m)} \end{aligned} \]

如果不等于1，則$m = k \times p(k \geqslant 2)$

設$m = s \times p^r,\gcd(s,p^r) = 1 = \gcd(s,p)$

則

\[p^{\varphi(s)}\equiv 1 \pmod s \]

又有$\varphi(m) = \varphi(p^r) \times \varphi(s)$

那么$p^{\varphi(m)} \equiv 1^{\varphi(p^r )}\equiv 1 \pmod s$--------------①

又因為

\[p^b = (p^{\varphi(m)})^{\lfloor \frac{b}{\varphi(m)} \rfloor} \times p^{b \operatorname{mod} \varphi(m)} \]

并由①：$(p^{\varphi(m)})^{\lfloor \frac{b}{\varphi(m)} \rfloor} \equiv 1^{\lfloor \frac{b}{\varphi(m)} \rfloor} \equiv 1 \pmod s$

故

\[p^b \equiv p^{b \operatorname{mod} \varphi(m)} \pmod s \]

\[p^{b + r} \equiv p^{b \operatorname{mod} \varphi(m)+ r} \pmod {s \times p^r} \]

(由引理)

則

\[p^{b + r} \equiv p^{b \operatorname{mod} \varphi(m)+ r} \pmod m \]

$p^{b+\varphi(m)}\equiv p^{b \operatorname{mod} \varphi(m)+ \varphi(m)}\pmod m$（同乘$p^{\varphi(m)-r}$）

由①：

\[p^{\varphi(m)+r} \equiv p^r \pmod {s \times p^r} \]

\[p^{\varphi(m)+r} \equiv p^r \pmod m \]

所以

\[\begin{aligned} p^b &\equiv p^{b - r} \times p^r \\&\equiv p^{b - r} \times p^{\varphi(m)+r} \\&\equiv p^{b + \varphi(m)} \\&\equiv p^{b \operatorname{mod} \varphi(m)+ \varphi(m)} \end{aligned} \pmod m \]

證畢

$Lucas$定理

\[C_{n}^{m} \equiv C_{n / p}^{m / p} \times C_{n \%p}^{m\%p} \pmod p \]

（$p$為素數）

證明：

首先：

\[\begin{aligned} C_{p}^{x} &\equiv \frac{p!}{x!(p - x)!} \\&\equiv \frac{p}{x}\times C_{p -1}^{x - 1} \\&\equiv p \times x^{-1}\times C_{p - 1}^{x - 1} \\&\equiv 0 \pmod p \end{aligned} \]

其中$0 < x < p,gcd(x,p) = 1$

所以$x$的逆元存在

再由上

\[\begin{aligned} (1 + x)^n &\equiv \sum\limits_{i = 0}^{n} C_{n}^{i}x^i \\&\equiv C_{n}^{0}\times 1 +C_{n}^{n} \times x^n \\&\equiv 1 + x^n \pmod p \end{aligned} \]

接下來

\[\begin{aligned} (1 + x)^n &\equiv \sum\limits_{i = 0}^{n} C_{n}^{i}x^i ---- \alpha \\&\equiv (1 + x)^{ap+b} \\&\equiv ((1 + x)^p)^a \times (1 + x)^b \\&\equiv (1 + x^p)^a \times (1 + x)^b \\&\equiv \sum\limits_{i = 0}^{a}C_{a}^{i}x^{ip} \times \sum\limits_{j = 0}^{b}C_{b}^{j}x^j -----\beta \pmod p \end{aligned} \]

有$x^m = x^{cp+d} = x^{cp} \times x^d$

由$\alpha,\beta$式和系數相等：

$C_{n}^{m} = C_{a}^{c} \times C_{b}^w0obha2h00$

再結合$n = ap + b,m = cp + d$

$C_{n}^{m} \equiv C_{n/ p}^{m / p} \times C_{n \%p}^{m\%p} \pmod p$

中國剩余定理（CRT）

若

\[\begin{cases} x \equiv r_1 \pmod {m_1}\\ x \equiv r_2 \pmod {m_2}\\ \cdots\\ x \equiv r_n \pmod {m_n} \end{cases} \]

$\forall1 \leqslant i < j \leqslant n,\gcd(m_i,m_j) = 1$

那么

\[x_{min+} = \sum\limits_{i = 1}^{n}r_ic_ic_i^{-1} \operatorname{mod} M \]

其中
$M = \prod\limits_{i =1}^{n}m_i$

$c_i = \frac{M}{mi}$

$c_i^{-1}$是$c_i$在模$m_i$意義下的逆元

證明：

首先：對$x \equiv r_i \pmod {m_i}$,先不求余

\[\begin{aligned} x &\equiv \sum\limits_{j = 1 \& j != i}^{n}r_jc_jc_j^{-1} + r_ic_ic_i^{-1} \\&\equiv \sum\limits_{j = 1 \& j != i}^{n}r_j\frac{m_i\times\frac{M}{m_i}(\in Z)}{m_j}c_j^{-1}+r_ic_ic_i^{-1} ---\frac{M}{m_i} \% m_i != 0 \\&\equiv 0+r_ic_ic_i^{-1} \\&\equiv r_i \pmod {m_i} \end{aligned} \]

再：

\[\begin{aligned} x_{min+} &\equiv x \% M \\&\equiv x +(-k)\times M \\&\equiv x --- m_i|M \pmod {m_i} \end{aligned} \]

擴展中國剩余定理（exCRT）

若$m_i$不一定兩兩互質

最直觀的：不求余中第一個注釋處將不成立（$\frac{M}{m_i} \% m_i != 0$互質時必成立，但不互質時不一定），無法進行后續計算

EX:

對于

\[x \equiv r_1 \pmod {m_1} \]

\[x \equiv r_2 \pmod {m_2} \]

轉化為

\[x = m_1p + r_1 = m_2q + r_2 \]

則

\[m_1p - m_2q = r_2 - r_1 \]

由裴蜀定理

$\gcd(m_1,m_2) | (r_2 - r_1)$時有解

特解與通解：（exgcd）

\[p = p_0 + \frac{m_2}{\gcd} \times k,q = q_0 - \frac{m_1}{\gcd} \times k \]

所以

\[x = m_1p + r_1 = m_1p_0 + \frac{m_1m_2}{\gcd}\times k + r_1 \]

那么

\[x \equiv m_1p_0 + r_1 \pmod {m_1m_2} \]

也就是說，兩個方程可以合并成一個方程：

\[x \equiv r \pmod m,r = m_1p_0 + r_1,m = \operatorname{lcm}(m_1,m_2) \]

合并$n - 1$次即可

ExLucas(與Lucas無關)

求

\[C_{n}^{m} \operatorname{mod} p \]

其中$p$不一定是質數

設

\[p = \prod\limits_{i = 1}^{k}p_i^{\alpha_i} \]

那么只需求

\[\begin{cases} C_{n}^{m} \operatorname{mod}p_i^{\alpha_i} \end{cases} \]

再用$CRT$合并即可（得到的是和$C_{n}^{m}$同余的最小正整數）

考慮求

\[C_{n}^{m} \operatorname{mod} p^k,p\in \operatorname{prime} \]

即

\[\frac{n!}{m!(n - m)!} \operatorname{mod} p^k \]

考慮到階乘可能包含$p$因子，所以先除干凈

即

\[\frac{\frac{n!}{p^x}}{\frac{m!}{p^y}\times \frac{(n - m)!}{p^z}} \times p^{x - y - z} \operatorname{mod} p^k \]

其中$x,y,z$均為對應階乘中含有的$p$因子數量

則再求

\[\frac{n!}{p^x} \operatorname{mod} p^k \]

（分母那倆求逆元就行了）

考慮按是否是$p$的倍數劃分階乘

\[\begin{aligned} n! &= \prod\limits_{i = 1}^{n}i \\&= \prod\limits_{i = 1}^{\lfloor\frac{n}{p}\rfloor}(i \times p) \times \prod\limits_{j = 1,j \% p != 0}^{n}j \\&= p^{\lfloor\frac{n}{p}\rfloor} \times (\lfloor\frac{n}{p}\rfloor)! \times \prod\limits_{j = 1,j \% p != 0}^{n}j \end{aligned} \]

對于后面一坨，考慮到$\operatorname{mod}$有循環節，后面循環的部分可以直接“掏”掉若干次方的模數成為第一部分的循環節

比如：

\[(1 \times 2 \times 4 \times 5) \times(10 \times 11 \times 13 \times 14) \equiv (1 \times 2 \times 4 \times 5)^2 \pmod 9 \]

其中后半部分循環節可以掏掉一個$9$變成第一部分

那么

\[\prod\limits_{j = 1,j \% p != 0}^{n}j = (\prod\limits_{i = 1,i \% p != 0}^{p^k}i)^{\lfloor\frac{n}{p^k}\rfloor} \times (\prod\limits_{i = p^k\times\lfloor\frac{n}{p^k}\rfloor,i \% p != 0}^{n}i) \]

前半部分是掏完模數的所有循環節，可以并成乘方，后半部分是剩的

所以

\[n! = p^{\lfloor\frac{n}{p}\rfloor} \times (\lfloor\frac{n}{p}\rfloor)! \times (\prod\limits_{i = 1,i \% p != 0}^{p^k}i)^{\lfloor\frac{n}{p^k}\rfloor} (\prod\limits_{i = p^k\times\lfloor\frac{n}{p^k}\rfloor,i \% p != 0}^{n}i) \]

第一項要除掉，但第二項中可能還有$p$因子

所以定義

\[f(n) = \frac{n!}{p^x} \]

\[f(n) = f(\lfloor\frac{n}{p}\rfloor)(\prod\limits_{i = 1,i \% p != 0}^{p^k}i)^{\lfloor\frac{n}{p^k}\rfloor} (\prod\limits_{i = p^k\times\lfloor\frac{n}{p^k}\rfloor,i \% p != 0}^{n}i) \]

回到原式，即求

\[\frac{f(n)}{f(m)f(n - m)}p^{x - y - z} \operatorname{mod} p^k \]

接下來求$x,y,z$

令$g(n) = x$（就是$n$的階乘中有多少個$p$因子）

結合$n!$的展開式，可得

\[g(n) = \lfloor \frac{n}{p}\rfloor + g(\lfloor \frac{n}{p}\rfloor) \]

so~

\[C_{n}^{m} \operatorname{mod} p^k = \frac{f(n)}{f(m)f(n - m)}p^{g(n) - g(m) - g(n - m)} \operatorname{mod} p^k \]

\[f(n) = \frac{n!}{p^x} \]

\[g(n) = x \]

合并即可

容斥原理

\[|\mathop{\bigcup}\limits_{i = 1}^{n}A_i| = \sum\limits_{i = 1}^{n}|A_i| - \sum\limits_{i < j}|A_i \cap A_j| + \sum\limits_{i < j < k}|A_i \cap A_j \cap A_k| - \cdots + (-1)^{n - 1}|A_1 \cap A_2 \cap \cdots \cap A_n| \]

奇數個集合交集個數的系數為正，偶數個集合交集個數的系數為負

~~這實在沒法證就那樣不斷修正后就這樣了~~

3.乘法逆元

定義：若$a \times x \equiv 1 \pmod b$,則$x$是$a$在模$b$意義下的乘法逆元，記為$a^{-1}$

使用：$(a/b) \% p = a \times b^{-1} \% p$

方法	條件	時間復雜度	備注
費馬小定理	模數為素數	$O(\log n)$
歐拉定理	$\gcd(a,p) = 1$	$O(\sqrt{n})$
擴展歐幾里得	$\gcd(a,p) = 1$	$O(\log n)$	可以判斷是否互質
線性遞推	模數為素數	$O(n)$

exgcd:求$ax+by=1$中$x$的最小正整數解（如果有的話）

Fermat:可知$a^{p - 1} \equiv 1 \pmod p$

即$a \times a^{p - 2}\%p \equiv 1 \pmod p$

則$a^{p - 2} \% p$為逆元，快速冪求解

Euler:類似于Fermat,$a^{\varphi(p)-1}$為逆元

線性：對于質數$p$,求$1,2,\cdots,p - 1$的逆元

設$p = k \times i + r(1<i<p,r <i)$

則$k \times i + r \equiv 0 \pmod p$

則

\[k \times i \times i^{-1} \times r ^{-1} + r \times i ^{-1} \times r ^ {-1} \equiv 0 \pmod p \]

\[k \times r ^{-1} + i^{-1} \equiv 0 \pmod p \]

\[i^{-1} \equiv -k \times r ^{-1} \pmod p \]

\[i ^{-1} \equiv - \lfloor \frac{p}{i} \rfloor \times r ^{-1} \pmod p \]

\[i ^{-1} \equiv - \lfloor\frac{p}{i}\rfloor \times (p\mod i)^{-1} \pmod p \]

即$inv[i] = - p / i \times inv[p \%i]$

$inv[1] = 1$

保證非負：$inv[i] = (p - p / i) \times inv[p \% i] \% p$

4.結論/引理

任意互質的$a,n$,滿足$a^x \equiv 1 \pmod n$的最小x一定是$\varphi(n)$的約數

證明：若不是，則有

$x \times k +r = \varphi(n)(r < x,k \in Z)$

由已知：$a^x \equiv a^{\varphi(n)} \equiv 1 \pmod n$

則有$a ^ {x \times k} \equiv 1^ k \equiv 1 \pmod n$

進一步的：$a^{x \times k + r} \equiv a ^ r \pmod n$ ------- a

又因為$x$已經最小，那么$a^r $模$n$一定不為1（$r < x$）

又由式子a可得：$1\equiv a ^{\varphi(n)} \equiv a^r \pmod n$

矛盾！

$\gcd(a,b) = \gcd(a + k \times b,b)$

證明：

設$\gcd(a,b) = d$

則$a = p\times d,b = q \times d(gcd(p,q) = 1)$

則

\[\begin{aligned} \gcd(a+k \times b,b) &= \gcd(pd+kqd,dq) \\&= \gcd(d(p + k \times q),dq) \\&= d \times \gcd(p+k \times q,q) \end{aligned} \]

設$m | p+k \times q,m|q$,則$m | p$

則$\gcd(p+k \times q,q) = m = 1$

則$\gcd(a+k \times b,b) = d$

若$a \equiv b \pmod m$,則$a \times k \equiv b \times k \pmod {m \times k}$

證明：
$a = s \times m + r$

$b = t \times m + r$

$a \times k - b \times k = (s - t)\times m \times k$

則$a \times k \equiv b \times k \pmod {m \times k}$

組合

常見策略

特殊位置（元素）優先
相鄰元素整體法（注意整體內部的排序與組合）
不相鄰問題插空法
定序問題倍縮法（總數 / 定序部分的全排列數）
排列問題求冪法
環排問題線排策略

一般的，$n$個元素做圓形排列，排法為$(n - 1)!$種

從$n$個不同元素中選擇$m$個元素排列，排法為$A_{n}^{m}/m$種
多排問題直排策略
混合問題先選（$C$）后排（$A$）
平均分組問題除法策略
重排列（多部分定序）
隔板法：將$n$個物體分成$m$堆,每堆至少一個

等價為：在$n - 1$個間隔中插入$m - 1$個隔板（分成$m$部分）

允許堆空：$C_{n + m - 1}^{m - 1}$

錯位排序

\[D(n) = (n - 1) \times (D(n - 1) + D(n - 2)) \]

Catalan數

定義

\[H(0) = 1,H(1) = 1 \]

\[H(n) = \sum\limits_{i = 0}^{n - 1}H(i)\times H(n - 1 - i) \]

\[\begin{aligned} H(n) &=C_{2n}^{n} - C_{2n}^{n-1} \\&= \frac{(2n)!}{n!n!} - \frac{(2n)!}{(n - 1)!(n + 1)!} \\&= \frac{(2n)!}{n!(n - 1)!}(\frac{1}{n} - \frac{1}{n+1}) \\&= \frac{(2n)!}{n!(n-1)!} \times \frac{1}{n(n + 1)} \\&= \frac{(2n)!}{n!n! \times (n+1)} \\&= \frac{1}{n+1}C_{2n}^{n} \end{aligned} \]

\[H(n) = \frac{4n-2}{n + 1}H(n - 1) \]

應用：

(1).（典例/特征）從$(0,0)$走到$(n,n)$,且路徑不超過對角線的路徑總數為$H(n)$

證明：

路徑總數：$C_{2n}^{n}$（共$2n$步，其中$n$步向上/右）

對角線：$y = x$

非法路徑超過對角線，說明與$y = x + 1$有交點

將該交點以后的路徑關于$y = x + 1$對稱，終點變為$(n + 1,n - 1)$

也就是說，所有非法路徑其實就是從$(0,0)$到$(n + 1,n - 1)$的所有路徑

那么合法路徑就是$C_{2n}^{n} - C_{2n}^{n-1}$

(2).$n$個元素進棧序列為$1,2,\cdots,n$，則出棧序列總數 = $H(n)$

將進棧抽象為走格子中向右走，出棧抽象為走格子中向上走，又因為一個元素進一次出一次，共$2n$次，那么就相當于：

從$(0,0)$走到$(n,n)$，任意時刻向上走的步數不能超過向右走的步數（出$>$入），也就是不超過對角線

顯然的卡特蘭數

(3).$n$對括號，能夠匹配的序列總數

一共$2n$個符號，左括號$n$個，右括號$n$個，記答案為$f(2n)$（顯然，括號里為字符數）

很顯然，匹配的序列滿足：任意一對括號中必有偶數個字符

我們選定一組括號作為分界，命名為括號$W$，左括號在第$0$位，那么右括號在
$0 + 2 \times k$（中間括號個數）$ + 1 = 2k + 1$處

每一個括號$W$的分布，對答案的貢獻是

括號$W$內部的括號匹配排列數 $\times$ 括號$W$外的括號匹配序列數

比如：括號$W$的位置為$0,3$,那么內部有$2$個字符，外部有$2n - 2 - 2 = 2n - 4$個字符，那么貢獻就是

\[f(2) \times f(2n - 4) \]

那么

\[ans = \sum\limits_{i = 1}^{n - 1}f(2i) \times f(2n - 2 - 2i) \]

由于自變量是字符個數 $= 2 \times$括號個數$n$，實際上這個答案改成以個數為自變量就是

\[\begin{aligned} ans &= \sum\limits_{i = 1}^{n - 1}f(\frac{2i}{2}) \times f(\frac{2n - 2 - 2i}{2}) \\&= \sum\limits_{i = 0}^{n - 1}f(i)\times f(n - 1 - i) \end{aligned} \]

形式決定本質：鑒定答案為$H(n)$

類似的想法還有

$n$個節點的不同二叉樹排列形式

非根結點總數$n - 1$，分成兩部分（左右子樹）排，無了，$H(n)$

一個凸多邊形（頂點數為$n$）劃分成三角形區域的方法數

先選定一個三角形把多邊形分成兩部分，該三角形占用3個頂點，那么左右的多邊形節點總數為$n +1$個（三角形的一個頂點會被算兩次）

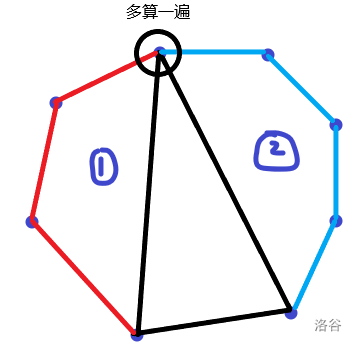
那么

\[ans = \sum\limits_{i = 2}^{n - 1}f(i)\times f(n + 1 - i) \]

總和為$n - 1$時答案為$H(n)$，那么此時答案就是$H(n - 2)$

總結：$Catalan$數的運用場景

任取一個集合作為選定集合$K$，能將全集$U$（所有元素，大小為$n$）分成兩個子集$S,T$，且兩子集的大小的和一定，設為$sum$(具體數值依題而定)
那么每一種分割情況對答案的貢獻就是

\[f(|S|) \times f(sum - |S|) = f(|S|) \times f(|T|) \]

對應答案就是$H(n - (sum - (n - 1)))$
注意：$S,T$中的元素必須全部等價（括號和括號等價之類，不會受到元素性質影響），否則貢獻成為$C_{sum}^{|S|} \times f(|S|) \times f(|T|)$

典例：P2606 排列計數，由于排列受大小影響，所以前面的組合數無法消去

對應一下：

括號類型中，選定集合為一組（個）括號，剩余括號根據是否在選定括號內分成兩個集合，并且由于每次的選定集合大小一定，所以這兩個集合大小之和一定
二叉樹的排列中，選定集合為根節點，剩余節點根據左右子樹分為兩個集合，且由于根節點只有一個，所以這兩個集合大小之和一定
典例中的走格子也是，不計非法時的和為$2n$，但是有一半的路徑會被砍掉，和變成$n$,又因為$|S|=|T|$屬于邊界條件算一次，所以和變為$n - 1$

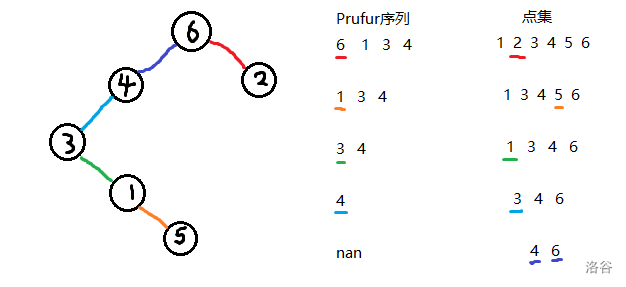
Prufur序列

$Prufur$序列是用一個序列來表示無根樹的東西，對于一顆$n$個節點的無根樹，可以構造出唯一確定的長度為$n - 2$的$Prufur$序列

構造：

$Tree -> Prufur$

找到編號最小的葉子結點，將它的父節點計入序列
刪去該葉子結點
重復上述過程直到剩下兩個節點

如圖

$Prufur -> Tree$

初始化一個點集為所有點
取出$Prufur$序列最前面的元素$x$
取出點集中不在$Prufur$序列中的最小編號$y$
連邊，刪去x,y
重復上述過程，在點集中最后剩下的兩個點之中連一條邊

如圖

（還是以上圖中的樹為例）

性質：

一一對應
度數為$d_i$的節點會在序列中出現$d_{i - 1}$次

其中，一一對應（雙射）是非常有用的一條性質，這個性質可以讓我們對數列（而不是樹）進行排列組合以獲得方案數而且不用擔心重復（一個序列只對應一棵樹，序列不同，樹一定不同）

應用：

無向完全圖的生成樹數量：$n^{n - 2}$

很好理解：$n - 2$個空，每個空上可填$1 \sim n$

第$i$個節點的度數為$d_i$ :

\[\frac{(n - 2)!}{\prod\limits_{i = 1}^{n}(d_i - 1)!} \]

這就是一個重排列問題

如果有$k$個節點能進入序列，那么每個節點的出現次數一定是$d_i - 1$，由重排列得到$\frac{A_{n - 2}^{n - 2}}{\prod\limits_{i = 1}^{k}A_{d_i - 1}^{d_i - 1}}$

又因為$(1 - 1)! = 0$所以葉子節點的度不影響結果，索性從$1$到$n$計算（也省去了求$k$的時間）

實際中，卻總有一些逆天情況

若干節點的度數沒有限制

設有$m$個節點沒有度數限制，有$k$個節點有度數限制

設$sum = n - 2 - \sum\limits_{i = 1}^{k}(d_i - 1)$，表示剩下的節點還能出現幾次

把未知度數的節點視為一個整體，運用重排列得到方案數：$\frac{A_{n - 2}^{n - 2}}{\prod\limits_{i = 1}^{k}A_{d_i - 1}^{d_i - 1}\times sum!}$

再考慮這個整體內部的方案數，由于無度數限制，直接隨便排

\[ans = \frac{A_{n - 2}^{n - 2}}{\prod\limits_{i = 1}^{k}A_{d_i - 1}^{d_i - 1}\times sum!} \times m^{sum},sum = n - 2 - \sum\limits_{i = 1}^{k}(d_i - 1) \]

BSGS

已知$a,b,p,\gcd(a,p) = 1$，求

\[a^x \equiv b \pmod p \]

的最小非負整數解

由擴展歐拉定理：$a^x \equiv a^{x \operatorname{mod} \varphi(p)}\pmod p$

因為$\varphi(p) \leqslant p - 1 < p$，所以$[0,p - 1]$中一定有解

設$x = im - j,m = \lceil \sqrt{p} \rceil,i \in [1,m],j \in [0,m - 1]$

則

\[a^{im-j} \equiv b \pmod p \]

\[(a^m)^i \equiv ba^j \pmod p \]

先枚舉$j$，求出$ba^j$，用unordered_map存儲$(ba^j,j)$，如果關鍵字重復，用$j$大的替代舊的

再枚舉$i$,求出$(a^m)^i$，如果表中有相同的結果，找到第一個（$j$最大）就結束，$ans = im - j$

斯特林數

第一類斯特林數： $\begin{bmatrix}n\\m\end{bmatrix}$

組合意義：讓$n$個人坐$m$個圓桌（大小足夠且不能有空桌）的方案數

遞推：

\[\begin{bmatrix}n\\m\end{bmatrix} = \begin{bmatrix}n-1\\m - 1\end{bmatrix} + (n - 1)\begin{bmatrix}n - 1\\m\end{bmatrix} \]

解釋：對于一個人，可以讓他單獨占一張桌子，也可以先讓剩下$n - 1$個人坐$m$張桌子，然后把這個人插入這些人的左邊，共$n - 1$種方案

第二類斯特林數：$\begin{Bmatrix}n\\m\end{Bmatrix}$

組合意義：將$n$個球放入$m$個盒子中（均相同而且要求非空）的方案數

與前者區別：圓桌即圓排列，但盒子內沒有次序

遞推：

\[\begin{Bmatrix}n\\m\end{Bmatrix} = \begin{Bmatrix}n - 1\\m - 1\end{Bmatrix} + m\begin{Bmatrix}n-1\\m\end{Bmatrix} \]

解釋：對于一個小球，可以讓他單獨占一個盒子，或者其他小球先放，他隨便放入一個盒子

posted @ 2024-02-17 12:33 why?123 閱讀(41) 評論(0) 收藏舉報

刷新頁面返回頂部

方法	條件	時間復雜度	備注
費馬小定理	模數為素數	\(O(\log n)\)
歐拉定理	\(\gcd(a,p) = 1\)	\(O(\sqrt{n})\)
擴展歐幾里得	\(\gcd(a,p) = 1\)	\(O(\log n)\)	可以判斷是否互質
線性遞推	模數為素數	\(O(n)\)

蒟蒻之淚

數論+組合

注：引理見后面第四部分

1.歐拉函數，歐拉篩及應用

1.歐拉篩：

2.歐拉函數：\(\varphi(n)\)

2.定理

歐拉定理：

裴蜀定理

推廣1：存在\(x,y\),使得

推廣2：存在\(X_1 \cdots X_n\),使得

擴展歐幾里得

通解：

擴展歐拉定理

\(Lucas\)定理

中國剩余定理（CRT）

擴展中國剩余定理（exCRT）

ExLucas(與Lucas無關)

容斥原理

3.乘法逆元

定義：若\(a \times x \equiv 1 \pmod b\),則\(x\)是\(a\)在模\(b\)意義下的乘法逆元，記為\(a^{-1}\)

4.結論/引理

任意互質的\(a,n\),滿足\(a^x \equiv 1 \pmod n\)的最小x一定是\(\varphi(n)\)的約數

矛盾！

\(\gcd(a,b) = \gcd(a + k \times b,b)\)

若\(a \equiv b \pmod m\),則\(a \times k \equiv b \times k \pmod {m \times k}\)

組合

常見策略

特殊位置（元素）優先

相鄰元素整體法（注意整體內部的排序與組合）

不相鄰問題插空法

定序問題倍縮法（總數 / 定序部分的全排列數）

排列問題求冪法

環排問題線排策略

多排問題直排策略

混合問題先選（\(C\)）后排（\(A\)）

平均分組問題除法策略

重排列（多部分定序）

隔板法：將\(n\)個物體分成\(m\)堆,每堆至少一個

錯位排序

Catalan數

(1).（典例/特征）從\((0,0)\)走到\((n,n)\),且路徑不超過對角線的路徑總數為\(H(n)\)

(2).\(n\)個元素進棧序列為\(1,2,\cdots,n\)，則出棧序列總數 = \(H(n)\)

(3).\(n\)對括號，能夠匹配的序列總數

\(n\)個節點的不同二叉樹排列形式

一個凸多邊形（頂點數為\(n\)）劃分成三角形區域的方法數

總結：\(Catalan\)數的運用場景

Prufur序列

BSGS

斯特林數

第一類斯特林數： \(\begin{bmatrix}n\\m\end{bmatrix}\)

第二類斯特林數：\(\begin{Bmatrix}n\\m\end{Bmatrix}\)

公告