「SOL」JOISC2021 解題報告
JOIS(egment-Tree)C
1. 前言
很早之前教練讓我們做這套題,我以為這套題應(yīng)該挺簡單,用幾天的空余時間就能刷完,結(jié)果預(yù)想的短周期刷題變成了長周期刷題……(好像是整個團(tuán)隊里最后一個刷完的??)
大多數(shù)題目(除了「保鏢」和「特技飛行」,我不知道把特技飛行這種題放 Day1 是不是想搞選手心態(tài) QwQ)還是能夠獨立地想出來,但是代碼長度堪憂,看了一下好像每道題的代碼都比其他人要長一些,不知道是不是實現(xiàn)細(xì)節(jié)的問題。話說過來雖然代碼要長一些,但是運行效率好像要快一些耶,目前「IOI 熱病」和「最差記者 4」都是 LOJ 的速度榜一 awa。
這一發(fā)是把線段樹給練爽了,真就 JOI Segment-Tree Camp 唄。
2. Day1 解析
2.1. IOI 熱病
2.1.1. 評析
推導(dǎo)「每個人行走方向其實固定」這一點比較考察貪心構(gòu)造的技巧。
而后面「李超線段樹上查全局最小值,支持刪除坐標(biāo)」這個有一定套路(我自己的做法,可能比較復(fù)雜),但是主要還是考察代碼實現(xiàn)能力。
2.1.2. 解析
先枚舉第一個人往哪個方向走,然后對其他人的最優(yōu)行走方向進(jìn)行分析。
不妨設(shè) ta 向上走,先考慮一些特殊的位置——考慮到能一個人與一個人相遇的人是米字格形狀的,所以先分析以起點為中心的米字格形狀。

- 顯然 1 區(qū)域只能向下,5 區(qū)域只能向上。
- 分析 2 區(qū)域,首先不可能向右向上;若向下,有一個非常巧妙的分析是「在時刻 \(i\) 出現(xiàn)感染的范圍是距離起點橫縱坐標(biāo)之差不超過 \(i\) 的位置」,手動模擬一下「可能出現(xiàn)感染的范圍」和 2 區(qū)域的人行走的情況,發(fā)現(xiàn)不可能被感染;于是只能向左。同理 8 區(qū)域只能向右。
- 分析 3 區(qū)域,不可能向右向下;若向上,同樣模擬「可能出現(xiàn)感染的范圍」和 3 區(qū)域行走的情況,不可能感染,所以只能向左。同理 7 區(qū)域只能向右。
- 分析 4 區(qū)域,不可能向右向下;若向左,同樣模擬「可能出現(xiàn)感染的范圍」和 4 區(qū)域行走的情況,發(fā)現(xiàn)只能向上。同理 6 區(qū)域只能向上。
分析得到這些區(qū)域只可能向一個方向走,于是我們大膽猜測其他區(qū)域也是這樣。實際上利用「可能出現(xiàn)感染的范圍」的分析同樣可以得到以下結(jié)論:
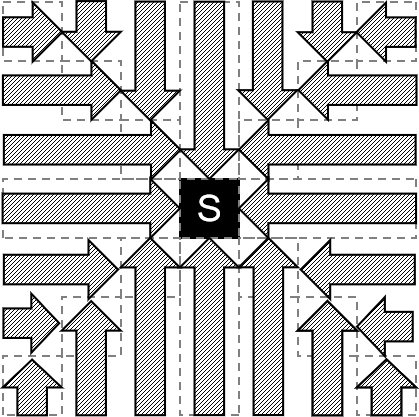
于是可以直接枚舉第一個人走的方向,然后固定其他人走的方向。
接下來其實就是模擬感染的過程了。兩個人相遇時可能會發(fā)生感染,但是必須要有一個人已經(jīng)感染。記 \(d_i\) 表示第 \(i\) 個人被感染的時刻。則在 \(\ge d_i\) 的時刻,第 \(i\) 個人才具備感染能力。發(fā)現(xiàn) \(d_i\) 其實就是最短路。
考慮用 Dijkstra 求最短路,設(shè)當(dāng)前點為 \(u=(x_u,y_u)\)。不妨設(shè) \(u\) 的行走方向為 \(y\) 正方向(即「向上」),\(u\) 能夠更新到的點只有:
- 左上右上的對角線上的人,若這個人在 \(v=(x',y')\),則相遇時間為 \(|x'-x_u|\),當(dāng) \(|x'-x_u|\ge d_u\) 時會感染,更新 \(|x'-x_u|\overset \min\to d_v\);
- \(u\) 行走方向上的人 \(v=(x_u,y')\),則相遇時間為 \(\frac {y'-y_u}2\),當(dāng) \(\frac {y'-y_u}2\ge d_u\) 時會感染,更新 \(\frac {y'-y_u}2\overset \min\to d_v\);
我們發(fā)現(xiàn)每次更新,都是將對角線上或同行同列上,\(x\) 坐標(biāo)(或 \(y\) 坐標(biāo))在某個范圍內(nèi)的點的 \(d\) 更新為一個關(guān)于 \(x\) 或 \(y\) 的一次式。于是可以對每條對角線、每行每列維護(hù)一棵李超線段樹,每次區(qū)間插入一條直線,支持查找全局最小點。一個區(qū)間的最小點一定在端點取到,直接更新即可。
這樣更新是支持了,但是 Dijkstra 還需要「彈出當(dāng)前點」,也就是將當(dāng)前這個 \(d\) 最小的點刪除。李超線段樹不是不支持刪除嗎?李超線段樹不支持刪除已經(jīng)插入的直線,但是可以刪除要考慮的點。我們可以給已經(jīng)刪除的點打標(biāo)記,更新區(qū)間最小值時找到左右兩端的未被刪除的點,這種「只有刪除,查找下一個未刪除的點」的操作實際上是一個并查集的套路。
可能就是并查集運行效率非常高,使我的代碼運行速度比其他人要快吧。
時間復(fù)雜度瓶頸在于李超線段樹區(qū)間插入線段,\(\mathcal O(n\log^2n)\),常數(shù)較大。
2.1.3. 源代碼
考慮到直接粘貼代碼會使文章長度爆炸,這里直接附上 LOJ 的提交記錄。
> Link LOJ - IOI熱病 參考代碼
2.2. 飲食區(qū)
2.2.1. 評析
部分分算法特別多,比較考驗選手對各種算法的熟悉程度。
一開始我想的是分塊,然后空間卡不過去……
2.2.2. 解析
刪除操作非常麻煩。如果沒有刪除操作,那么我們可以整體二分,對每個查詢找到第一次隊列的人數(shù)大于等于 \(B_i\) 的時候。
考慮刪除會產(chǎn)生什么影響。我們嘗試「不真的進(jìn)行刪除操作」,而是把查詢給定的位置 \(B_i\) 向后移動離開的人數(shù)。注意到隊列可能小于 \(K_i\),不能直接向后移動 \(K_i\)。
用線段樹分別維護(hù)「不考慮刪除操作,當(dāng)前隊列有多少人」,以及「考慮刪除操作,當(dāng)前隊列有多少人」。第一種就是區(qū)間加、單點查;第二種稍麻煩,每次有刪除操作時,需要全部元素對 \(0\) 取 \(\max\),但是只涉及單點查詢,可以直接維護(hù)形如 \(x'=\max\{x+a,b\}\) 的懶標(biāo)記 \((a,b)\),而不用 Segment Tree Beats! 。
兩個值的差就是詢問前離開的人數(shù),然后就可以整體二分了。注意需要提前判斷是否無解。
時間復(fù)雜度 \(\mathcal O(n\log^2n)\)。
2.2.3. 源代碼
> Link LOJ - 飲食區(qū) 參考代碼
3. Day2 / Day3 解析
因為通信題暫時不做,然后「保鏢」這道題又完全不會,Day2Day3 就合起來了……
3.1. 道路建設(shè)
3.1.1. 評析
這道題硬上復(fù)雜數(shù)據(jù)結(jié)構(gòu)(樹套樹、KD樹)也能做,但是在考場上比較消耗時間。
如果多花些時間思考有沒有簡單一些的方法,反而可能節(jié)省時間。畢竟出題人只要不是想要出防 AK 題會考慮代碼的復(fù)雜程度。
3.1.2. 解析
顯然是要用數(shù)據(jù)結(jié)構(gòu)直接維護(hù)當(dāng)前花費最小的方案,支持把最小的方案刪除。
還是比較常見的套路,對每個點求出從它出發(fā)的最優(yōu)方案,全部塞進(jìn)堆里。每次從堆里取出全局最優(yōu)方案,將其刪除后找到對應(yīng)點的次優(yōu)方案。
曼哈頓距離有兩個絕對值,如果硬上數(shù)據(jù)結(jié)構(gòu)就需要樹套樹維護(hù)四個象限的點。但是題目規(guī)定起點終點交換本質(zhì)相同,我們可以直接把點按 \((x,y)\) 雙關(guān)鍵字排序,只考慮從較大的點出發(fā)到較小點的路徑。這樣一來 \(x\) 的絕對值就沒了。
現(xiàn)在的問題就是維護(hù) \((x,y)\lt(x_u,y_u)\) 的所有點中,\(y\) 在某個區(qū)間上的點的 \(\max\{-x-y\}\) 以及 \(\max\{-x+y\}\)。需要支持刪除指定的點。
不管刪除操作,那就是可持久化線段樹。加上刪除操作呢?那還是可持久化線段樹,只在當(dāng)前線段樹上刪除指定節(jié)點,把對應(yīng)位置賦值為 \(-\infty\) 即可。
時空復(fù)雜度為 \(\mathcal O((n+K)\log n)\)。
3.1.3. 源代碼
> Link LOJ - 道路建設(shè) 參考代碼
3.2. 聚會 2
3.2.1. 評析
個人認(rèn)為是一道比較一般的題目……僅僅是考察基礎(chǔ)的樹上信息維護(hù)的方法而已。
3.2.2. 解析
設(shè)出席者的點集為 \(S\),通過調(diào)整法(如果「開會地址」不符合下述條件,可以通過把它向某個方向調(diào)整,使代價不減,直到符合下述條件,即為代價最小的「開會地址」)可證明:
- 若 \(|S|\) 為偶數(shù),則「開會地址」可以取某條路徑上的所有點;
- 若 \(|S|\) 為奇數(shù),唯一的「開會地址」是 \(S\) 中距離其他點距離之和最小的點。
所以我們只需要回答 \(|S|\) 為偶數(shù)的的情況。不妨枚舉上述的「某條路徑」為 \((u,v)\),

\(S\) 可取的點集為 \(\{u,v\}\cup S_1\cup S_2\),并且 \(S\) 在 \(\{u\}\cup S_1\) 中的點數(shù)必須和 \(\{v\}\cup S_2\) 中的點數(shù)相等,類似于中位數(shù)。于是 \(dist(u,v)\) 可以貢獻(xiàn)到 \(|S|\le2(\min\{|S_1|,|S_2|\}+1)\) 的所有偶數(shù) \(|S|\) 的答案。
考慮樹形 DP,\(f(u,s)\) 表示 \(u\) 子樹內(nèi),子樹大小大于等于 \(s\) 的最深的點的深度。一邊轉(zhuǎn)移一邊貢獻(xiàn)到答案。\(s\) 不超過 \(u\) 的子樹大小,可以考慮 Dsu on Tree 進(jìn)行優(yōu)化,時間復(fù)雜度 \(\mathcal O(n\log n)\)。
但是我們發(fā)現(xiàn) Dsu on Tree 只能計算「折線型」的路徑,而不能計算祖先到后繼的路徑。分別考慮較小值在后繼方向和在祖先方向的情況:
- 后繼的子樹較小:在 DFS 時,用線段樹維護(hù)子樹大小大于后繼子樹的祖先的最小深度,或者利用單調(diào)性二分;
- 祖先的子樹較小:直接線段樹合并維護(hù)出當(dāng)前子樹內(nèi),子樹大小在某個區(qū)間內(nèi)的后繼的最大深度。
復(fù)雜度仍然是 \(\mathcal O(n\log n)\)。
3.2.3. 源代碼
> Link LOJ - 聚會 2 參考代碼
4. Day4 解析
4.1. 活動參觀 2
4.1.1. 評析
考察了非常經(jīng)典的字典序的貪心性質(zhì)以及選手選擇算法的能力。
與道路建設(shè)一題相同,用較簡單的算法往往可以節(jié)省大量時間。
4.1.2. 解析
先讀對題,字典序是將參加的活動按編號排序后再比較,而不是按參加時間比較。
于是貪心地從小到大判斷「是否可以參加第 \(i\) 個活動」。
假設(shè)要參加,首先 \(i\) 不能和已經(jīng)參加的活動沖突。
然后 \(i\) 會把原來的一個空閑時間段 \([L,R]\) 分成兩段 \([L,l_i],[r_i,R]\),記只考慮時間段 \([L,R]\),最多能夠參加的活動數(shù)量為 \(f(L,R)\)。則原本 \([L,R]\) 提供 \(f(L,R)\) 的貢獻(xiàn),現(xiàn)在只能提供 \(f(L,l_i)+f(r_i,R)+1\) 的貢獻(xiàn)。直接判斷剩余次數(shù)是否足夠即可。
怎么計算 \(f(L,R)\)?貪心地選取活動,每次選取可參加的右端點最小的活動,于是參加一個活動之后的下一個活動(的右端點)是唯一的,倍增即可。
4.1.3. 源代碼
> Link LOJ - 活動參觀 2 參考代碼
4.2. 最差記者 4
4.2.1. 評析
一道不錯的線段樹合并優(yōu)化 DP 的題,對這個技巧比較熟練的話應(yīng)該能一眼看出來。
如果想到利用 DP 數(shù)組的單調(diào)性維護(hù)差分?jǐn)?shù)組,可以在一定程度上簡化代碼,但是沒想到這點也能做。
4.2.2. 解析
把選手的 rating 的 “≥” 關(guān)系建為有向圖,\(u\to v\) 表示 \(u\) 的 rating 小于等于 \(v\) 的 rating。
每個點的入度為 \(1\),顯然每個連通塊是葉向基環(huán)樹,不同連通塊之間沒有影響。基環(huán)樹環(huán)上的點的 rating 必須相同,顯然最終環(huán)的 rating 只可能是 \(1\) 或者環(huán)上某個點原本的 rating。
最后枚舉環(huán)的取值,考慮對樹的部分進(jìn)行 DP。定義一個非常暴力的 DP 狀態(tài),\(f(u,w)\) 表示 \(u\) 的 rating 設(shè)為 \(w\),子樹內(nèi)的總花費的最小值。
然而這樣定義會使得 \(f(u,w)\) 有值的點很多,并且被分成前后綴兩個部分。考慮到 \(c_i\) 之和為定值,我們可以反過來定義 \(f(u,w)\) 為 \(u\) 取 \(w\),\(u\) 子樹內(nèi)減免的花費的最大值。
這樣比較方便之后線段樹合并。
轉(zhuǎn)移式中有后綴 \(\max\),并且是子樹求和合并的形式,可以用線段樹合并。我們發(fā)現(xiàn),后綴 \(\max\) 使得大多數(shù)位置都有值,如果在合并是直接新建節(jié)點下放懶標(biāo)記,會導(dǎo)致線段樹節(jié)點數(shù)爆炸,破壞線段樹合并的時間復(fù)雜度。但是后綴 \(\max\) 改變的位置數(shù)量只有子樹大小,稱改變的位置為「關(guān)鍵點」,則只需要維護(hù)關(guān)鍵點的值即可。
比較顯然的是 \(v_1,v_2\) 合并后的關(guān)鍵點就是 \(v_1,v_2\) 各自的關(guān)鍵點的并,于是在合并時維護(hù)兩棵線段樹各自的后綴 \(\max\) 即可。合并時若出現(xiàn)一棵線段樹已經(jīng)為空,會對另一棵線段樹產(chǎn)生「整體加上后綴 \(\max\)」的貢獻(xiàn),這意味著要打加法標(biāo)記。我們并不希望下放標(biāo)記,還好加法標(biāo)記比較簡單,可以采用標(biāo)記永久化。
整個代碼最復(fù)雜的部分就是線段樹合并的函數(shù),具體可以參考代碼。
4.2.3. 源代碼
> Link LOJ - 最差記者 4 參考代碼


 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號