題目傳送門：Click。

更好地觀感：Click（進入速度玄學）

某蒟蒻看見這道題，想了足足一個晚上，過后茅塞頓開，故作此篇。

感謝神犇的題解，思路基本相同，補充了一些自己的想法或這片題解可能沒有注意到的細節。

看題目數據范圍：\(1 \leqslant r,c \leqslant 10^6,1 \leqslant k \leqslant 10^{12}\)，顯然打暴力 \(\mathcal{O}(rc)\) 的時間復雜度是行不通的。必須做到近似于 \(\mathcal{O}(r)\) 的時間復雜度。

觀察題目：題目中說：當 \(x+y=x \oplus y\) 時，這個格子是灰色的。而最后所求的答案就是走過的灰色的格子數，很容易想到斜著劃分所有的格子，每一組的格子中的任意一個格子 \((x,y)\) 都滿足 \(x+y=S\)，其中 \(S\) 是不變的。如下圖：（圖可能有點丑，僅做示意）

接下來，我們針對某個特定的 \(S\) 進行考慮。設有一組 \((x,y)\)，那么 \(x \oplus y=S\) 必然滿足：\(S\) 二進制上的第 \(x\) 位為 \(1\)，則 \(x\) 與 \(y\) 的二進制第 \(x\) 位上必然不同；而當 \(S\) 二進制上的第 \(x\) 位為 \(0\)，那么 \(x\) 與 \(y\) 二進制第 \(x\) 位上必然相同。

再來考慮加法。首先看 \(S\) 二進制位的最后一個 \(1\)，發現它有兩種情況，通過后兩位進位，或是由 \(x,y\) 中一個 \(0\) 一個 \(1\) 相加而成。

當它是通過后兩位進位而成時，則 \(x,y\) 該位上相同則無法滿足異或；不同，則無法滿足相加（因為有進位）。（見下圖 1）

而它是由更前面的某一位 \(0\) 對應的 \(x,y\) 中的 \(1\)，也無法滿足要求。（見下圖 2）

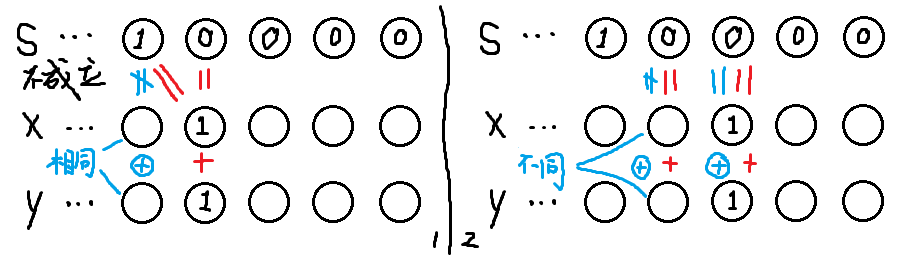
對于一個 \(S\)，我們可以把它分為若干如上形式的二進制段，也可得出相通的結論。綜上，在 \(S\) 的每一位 \(0\) 上，\(x\) 與 \(y\) 同為 \(0\) ；否則，\(x,y\) 有且僅有一個 \(1\)。

從這一點入手，統計某一斜行（由于斜行上各自數量可能不確定，我們這里用兩個數確定一斜行 \((x,y)\) 表示從 \((0,y)\) 走到 \((x,y-x)\)）上有多少個灰色格子（即 \(S=y\)），我們可以知道有一個 \(x^\prime \leqslant x\)，其中 \(x^\prime\) 二進制上的每一位 \(1\)，都對應了 \(x\) 與 \(y\) 上公共的 \(1\)。在這個 \(x^\prime\) 中，（對于一對二元組 \((p,q)\)，這一步相當于枚舉 \(x\) 的二進制位）我們可以知道 \(p\) 可以在這一位上取 \(1\)（\(q\) 取 \(0\)），或者取 \(0\)（\(q\) 相反）。而對于 \(y\) 某二進制位上為 \(1\)，而 \(x\) 該二進制位上不為 \(1\)，那么只可能 \(q\) 上取 \(1\)，而 \(p\) 上為 \(0\)。

簡單地說，就是將 \(y\) 分解成若干段形如 \(\texttt{1000...}\) 的二進制段，然后判斷這些“段”與 \(x\) 是否對應。如果其最高位 \(1\) 與 \(x\) 對應，那么說明這一位可以 \(1\)，答案加上后面的幾段（注意！這里并不要求與 \(x\) 對應！）分別取 \(0\) 或 \(1\) 的總方案數。當然，這樣算會少算一種情況，即所有對應二進制段上都取了 \(0\)。

理解了這個規律，我們可以寫出這樣一個用來統計某一斜行上灰色格子數量的函數：

ll type[64];
ll counting(ll x,ll y) {
	ll res=1LL,cnt=0;
	for(;y;res<<=1,y>>=1)
		if(y&1) type[++cnt]=res;
	res=0;
	for(ll i=cnt;i>0;--i)
		if(x-type[i]>=0) x-=type[i],res|=(1<<i-1);
	return res+1;
}

解釋說明：\(\operatorname{type}_i\) 表示 \(y\) 從高到低第 \(i\) 個 \(1\) 的權值。由于下標就相當于第幾段，然后直接一邊分解 \(x\) 一邊計算答案就行了。1<<i-1 表示第 \(i\) 段后面有 \(i-1\) 段，每段取或不取的總方案數為 \(2^{i-1}\)，由于每個二進制位都不會重復，可以直接用 |= 運算。

最后回到問題，統計走 \(k\) 步走過的灰色格子數，可以先統計從如下圖紅色部分的斜行的灰色格子數，然后統計如下圖綠色部分的灰色格子數，累加走過的格子。當走不完某一斜行時，暴力模擬一下就可以了。這里細節有點多，就不贅述了。

（其中灰色部分可以幫助統計綠色部分）

完整代碼：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
ll type[64];
ll counting(ll x,ll y) {
	ll res=1LL,cnt=0;
	for(;y;res<<=1,y>>=1)
		if(y&1) type[++cnt]=res;
	res=0;
	for(ll i=cnt;i>0;--i)
		if(x-type[i]>=0) x-=type[i],res|=(1<<i-1);
	return res+1;
}
ll n,m,k;

int main() {
	scanf("%lld%lld%lld",&n,&m,&k);
	int drct=1;
	if(m<n) swap(m,n),drct=0;
	ll ans=0,done=0;
	for(ll i=0;i<m;++i,drct^=1) {
		ll cnt=min(i+1,n);
		if(done+cnt<k) done+=cnt,ans+=counting(min(i,n-1),i);
		else {
			if(drct) for(ll p=min(i,n-1),q=i-min(i,n-1);done<k;--p,++q,++done)
				ans+=p+q==(p^q);
			else for(ll p=0,q=i;done<k;++p,--q,++done)
				ans+=p+q==(p^q);
			break;
		}
	}
	if(done==k) {
		printf("%lld\n",ans);
		return 0;
	}
	for(int i=1;i<n;++i,drct^=1) {
		ll cnt=n-i;
		if(done+cnt<k) done+=cnt,ans+=counting(n-1,m+i-1)-counting(i-1,m+i-1);
		else {
			if(drct) for(ll p=n-1,q=m-n+i;done<k;--p,++q,++done)
				ans+=p+q==(p^q);
			else for(ll p=i,q=m-1;done<k;++p,--q,++done)
				ans+=p+q==(p^q);
			break;
		}
	}
	printf("%lld\n",ans);
	return 0;
}

完。