若干字符串算法
Hash
將不知道什么東西映射到一個小范圍的數(shù)上。相比用map而言,手寫Hash往往會做到更高的效率。
Hash的一大用處是儲存和查詢兩個復雜數(shù)據(jù)的存在情況。這對于判斷多個字符串相等往往有很大優(yōu)勢。
在OI中有一種非常重要的Hash函數(shù),它的運轉方式如下:
把字符串\(s\)看成一個\(P\)進制數(shù),這樣就可以給每個數(shù)賦上一個正的權值。具體來說,它返回的是一個無符號的長整數(shù)(省去了取模操作),大小:
當\(P = 131\)或\(P = 13331\)時,沖突的概率極低。
另外,上面這個公式還有遞推版本和區(qū)間版本:(\(c\)是單個字符)
這樣,假設只有\(q\)個字符串,我們就可以用\(O(q|s|)\)的時間內處理每個字符串前綴的哈希值,并僅用\(O(1)\)判斷兩個字符串或者它們的子串是否相等了。
單詞背誦。我給出了一個長度為\(N(N \leq 1000)\)的單詞表,希望背下它們。但我打算通過閱讀文章來背誦它們。具體來說,我有一篇含單詞數(shù)為\(M(M \leq 10^6)\)的文章,而我會節(jié)選其中連續(xù)的一段,將其提取,并每天閱讀。我希望求出這篇文章中最多涵蓋了多少我單詞表里的單詞,并且在涵蓋極大單詞的情況下,我最短可以摘選多短的文章。
這里體現(xiàn)了Hash表的經(jīng)典應用,即快速查詢兩個字符串是否相等。可以預處理出文章和單詞表內所有單詞的哈希值,并二分查找文章中單詞對應單詞表里的單詞編號。此時問題變成了“涵蓋所有目標元素的極大子段”,先求出最多的單詞數(shù)\(cnt\),然后用兩個指針線性掃描文章。每擴展一次右邊界時,貪心地縮小左邊界,然后更新答案。預處理\(O(N\log N + M|s|\log N)\),而掃描是線性的。如果這道題對哈希值取合適的模數(shù),可以省去排序的步驟,把預處理降到\(O(M|s|)\);但為了防止哈希沖突,這里我們還是采用最穩(wěn)妥的做法。
inline ull Hash(char *str)
{
int len = strlen(str);
ull ret = 0;
RP(i, 0, len - 1) ret = ret * P + (str[i] - 'a' + 1);
return ret;
}
inline int bs(ull CH){
int l = 1, r = N;
while(l < r){
int mid = (l + r) >> 1;
if(HS[rev[mid]] >= CH)
r = mid;
else
l = mid + 1;
}
if(HS[rev[l]] == CH)
return rev[l];
else
return 0;
}
inline void init(){
RP(i, 1, N) HS[i] = Hash(S[i]), buf[i] = mp(HS[i], i);
sort(buf + 1, buf + N + 1);
RP(i, 1, N) disc[buf[i].second] = i, rev[i] = buf[i].second;
RP(i, 1, M) HT[i] = Hash(T[i]), match[i] = bs(HT[i]);
}
int main(){
N = qr(1);
RP(i, 1, N) scanf("%s", S[i]);
M = qr(1);
RP(i, 1, M) scanf("%s", T[i]);
init();
int l = 1, r = 1;
while(r <= M && cnt < N){
if(match[r] > 0 && buc[match[r]] == 0) ++ cnt;
++ buc[match[r]];
++ r;
}
if(cnt == 0){
puts("0");puts("0");
return 0;
}
r = 1; int tmp = 0; memset(buc, 0, sizeof(buc));
while(r <= M && tmp < cnt){
if(match[r] > 0 && buc[match[r]] == 0) ++ tmp;
++ buc[match[r]];
++ r;
}
-- r;
while(r <= M){
while(l < r){
if(buc[match[l]] == 1)
break;
if(buc[match[l]]) -- buc[match[l]];
++ l;
}
ans = min(ans, r - l + 1);
++ r; ++ buc[match[r]];
}
printf("%d\n%d", cnt, ans);
return 0;
}
附:ELFHash
偏工程向,但是還是可以拿來一用。其基本思想是每次載入當前字符的ASCLL碼,然后讓編碼相互雜糅,互相產生影響。具體的原理超出了本文的討論范圍,故這里只粘貼代碼:
inline ull Hash(char *str)
{
ull ret = 0, x = 0;
while(*str){
ret = (ret << 4) + *str;
if((x = ret & 0xf000000L) != 0){
ret ^= (x >> 24);
ret &= ~x;
}
++ str;
}
return (ret & 0x7fffffff);
}
順帶一提,最近使用這個ELFhash,結果出現(xiàn)了相當罕見的Hash沖突。只能說酌情使用吧。
KMP
KMP利用一個nxt數(shù)組維護了“如果當前不匹配,我應該從哪里開始匹配起”。它一定是針對模式串而言的。具體來說,它保存的是\(p(i)=\max\{j, S_{i - j + 1\cdots i} = S_{1\cdots j}\}\),即當前前綴子串中,最長的前綴和后綴相等的長度。可以結合下面這個圖理解一下:
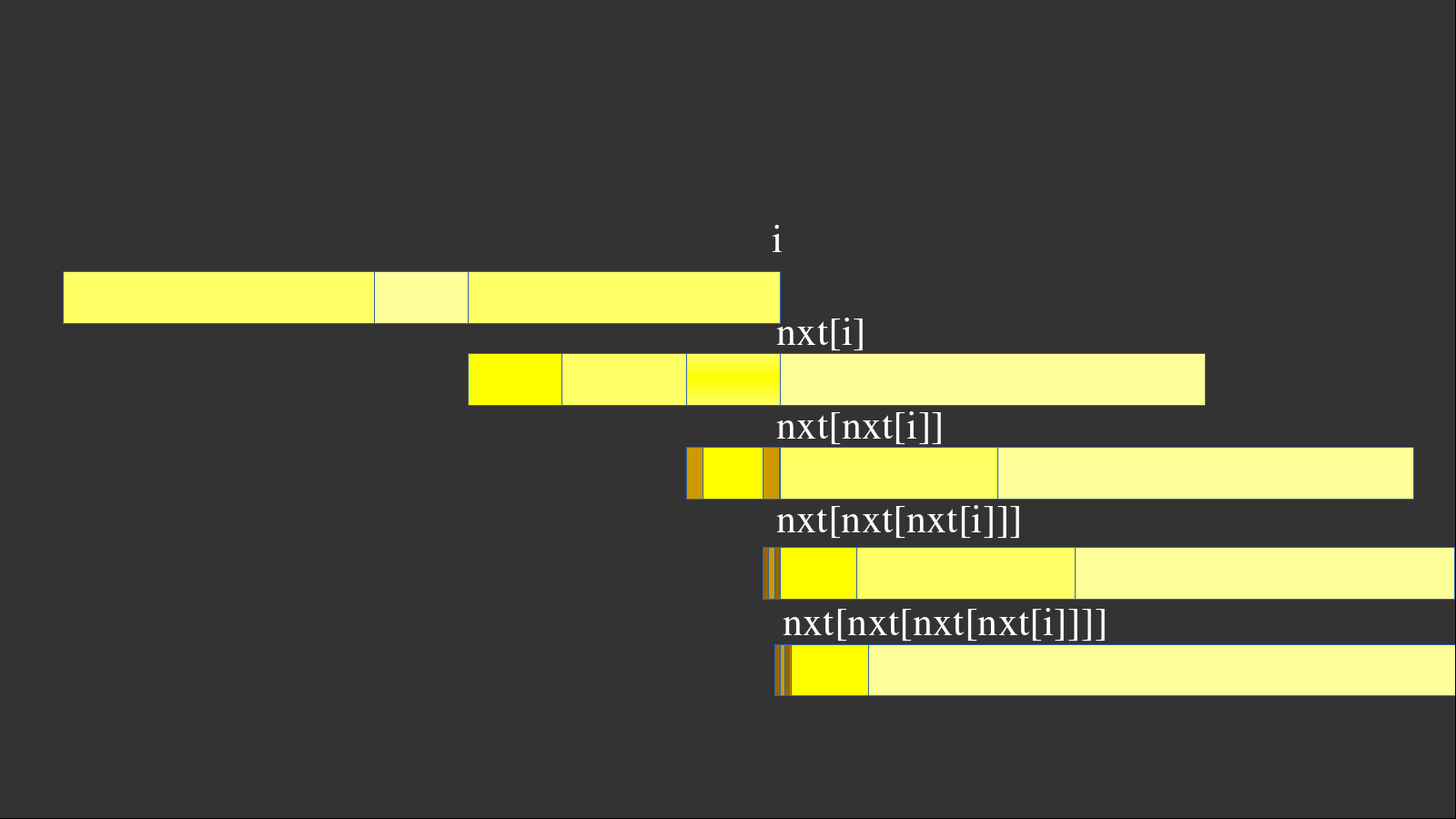
假設模式串\(S\)在\(1\cdots i\)都匹配,唯獨在\(i+1\)不匹配,我們就要重新匹配。但是,我們不需要從頭開始,而是從\(\text{nxt}(i)\)開始。因為\(1\cdots i\)均匹配,\(i-\text{nxt}(i)+1\cdots i\)顯然也一定匹配。由于最長性,我們從\(\text{nxt}(i)\)開始匹配一定更優(yōu)。
問題就在于,如何求\(\text{nxt}(i)\)?樸素的做法會達到\(O(|S|^2)\)。可以考慮這樣的思路:
假設我從\(i\)擴展到\(i+1\),如果恰好\(S_{\text{nxt}(i)+1} = S_{i+1}\),那顯然是最好的。
可大部分情況下不能直接擴展。我們需要在\(\text{nxt}(i)\)之前找到一個位置\(j\),使得\(S_{j+1} = S_{i+1}\),并令\(\text{nxt}(i+1) = j+1\)。這個過程正是一個KMP匹配的過程,因此可以把\(S\)本身當成一個文本串,用自己匹配自己。
不過很抱歉的是,目前我也不能太理解這個精妙的算法,因此只能先張貼代碼:
const int MAXL = 1e6 + 2;
char T[MAXL], S[MAXL]; int lT, lS;
int nxt[MAXL];
inline void init(){
nxt[1] = 0;
int r = 0;
RP(i, 2, lS){
while(r > 0 && S[r + 1] != S[i])
r = nxt[r];
if(S[r + 1] == S[i])
++ r;
nxt[i] = r;
}
}
inline void KMP(){
int r = 0;
RP(i, 1, lT){
while(r > 0 && S[r + 1] != T[i])
r = nxt[r];
if(S[r + 1] == T[i])
++ r;
if(r == lS)
printf("%d\n", i - lS + 1), r = nxt[r];
}
}
int main(){
scanf("%s", T + 1);
scanf("%s", S + 1);
lT = strlen(T + 1), lS = strlen(S + 1);
init();
KMP();
RP(i, 1, lS) printf("%d ", nxt[i]);
return 0;
}
只能說這個算法和樹狀數(shù)組一樣,寫起來和記起來都不算難,但如何理解卻有相當大的難度。
manacher
回文串的定義:若一個字符串的每一個字符\(S_i\)都滿足\(S_i = S_{|S|+1-i}\),則\(S\)是一個回文串。當然,一個串\(S\)本身可能不是回文串,但它一定存在至少\(|S|\)個回文子串。(單個字符也要考慮!)一個回文子串的直徑就是它的長度。現(xiàn)在請你求出一個字符串\(S\)的所有回文子串中最長的回文直徑。
回文串的判定比較復雜,分為奇回文串(形如\(ABA\))和偶回文串(形如\(BB\))。為了方便判定,我們在相鄰的字符之間加入'#'號,從而將任意回文串的判定改為“奇回文串的判定”。這等價于插入\(S_{0.5},S_{1.5},\cdots\)等字符。
上面我所提到的“回文直徑”可以直接無視,因為比它更重要的是回文半徑:對于一個長度為\(d\)的奇回文串,它的回文半徑\(r = \frac{1}{2}(d-1)\)。考慮對于每一個字符,用暴力拓展回文半徑的算法,可以做到\(O(N^2)\)。有沒有更快的呢?
算法中一個非常重要的優(yōu)化手段就是利用已知信息,用空間換時間。我們考慮若干個回文半徑之間的關系,發(fā)現(xiàn)了一個重要的關系:當先前某個點的回文半徑足夠大,足以覆蓋當前帶擴展點時,我們可以直接繼承先前的答案。什么意思呢?請看下圖:
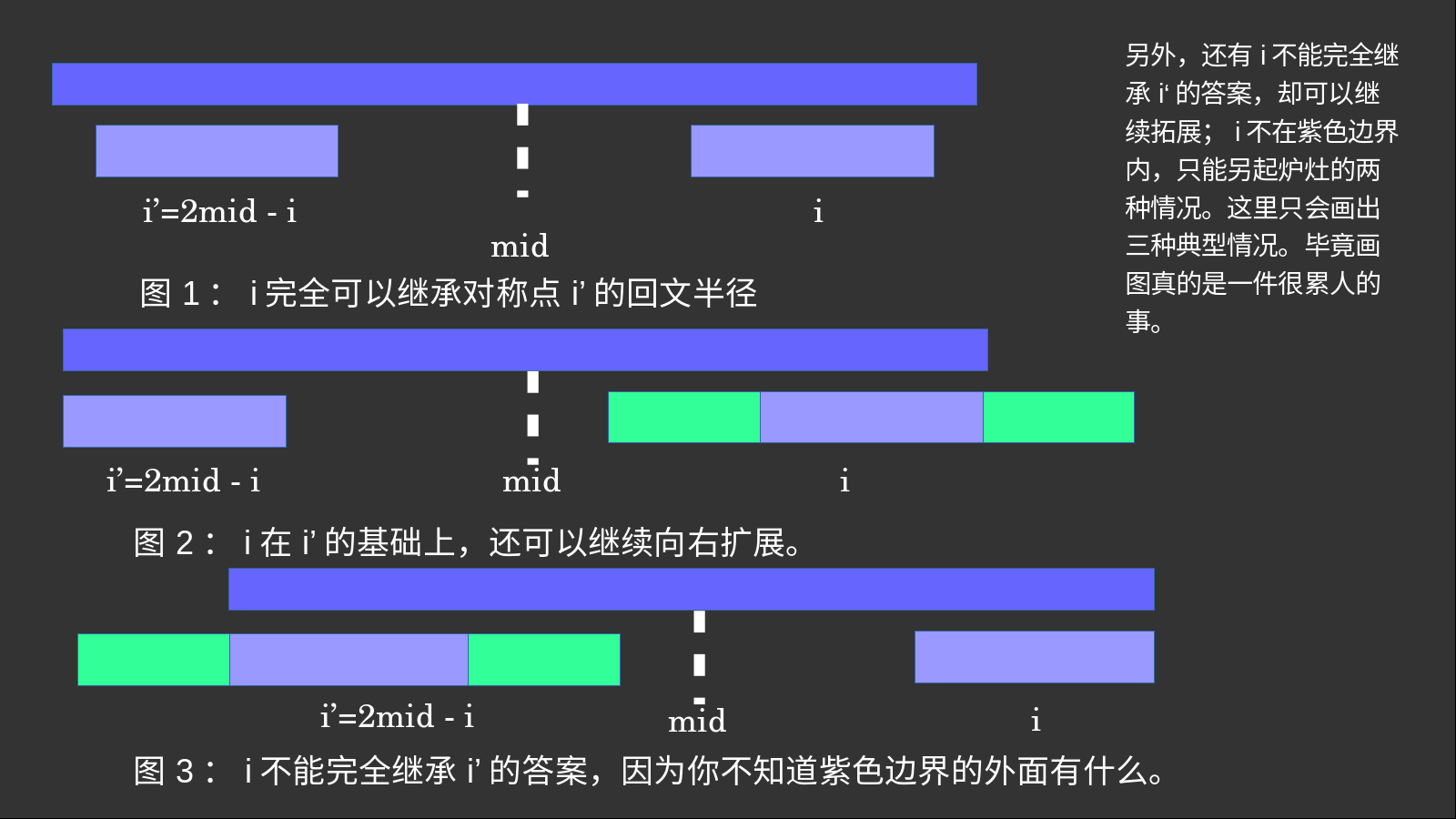
如果當前待求的回文中心\(i\)在一個足夠長的回文串內,且\(i\)形成的回文串足夠小,那么一定存在一個\(i'\)與\(i\)關于\(mid\)對稱,且這兩個回文串的長度是完全相同的。因此,\(i'\)的答案可以直接傳給\(i\)。
當然,還有兩種特殊情況:
- \(i\)可以擴展到青色的部分,而\(i'\)做不到。這種情況下直接在\(i'\)的回文半徑的基礎上,繼續(xù)向右擴展即可。
- \(i'\)可以擴展到青色的部分,而\(i\)做不到。此時\(i\)最多只能繼承\(R-i\)大小的半徑(即擴展的邊界不能超過紫色邊界)
情況很多,但是可以直接令當前回文半徑\(r(i) = \min(r(i'), R - i)\),然后再嘗試向右擴展\(r(i) = r(i) + \delta r\)就可以了。這個做法可以解決一切問題。
每次維護當前回文串的最右邊界\(R\),就可以盡可能多地覆蓋到小回文串。由于回文串可以\(O(1)\)繼承在當前“大回文串”內的所有答案,這個算法可以做到\(O(N)\)。
順便注意一下,為了防止擴展越界,我們會在整個字符串\(S\)的最前面和最后面加上一個特殊字符表示邊界,比如$ * @等。當然,你也可以直接用if特判。
最后一定要注意,上述操作都是對于加入#的字符串而言。原串的最長回文子串長度,應該等于當前串中的\(r\mid_{\max} - 1\)。
int main(){
scanf("%s", buf);//buf是一個臨時輸入數(shù)組
int len = strlen(buf);
S[1] = '#';
RP(i, 0, len - 1){
S[(i + 1) << 1] = buf[i];
S[((i + 1) << 1) + 1] = '#';
}
len = (len << 1) + 1;
S[0] = '$', S[len + 1] = '@';//起始符和終止符,防止越界。另外,這兩個字符一定要不同,不然會誤判“整個字符串都是回文串”的情況。
RP(i, 1, len){
if(i <= R)
r[i] = min(r[(mid << 1) - i], R - i);
else
r[i] = 1;
while(S[i - r[i]] == S[i + r[i]]) ++ r[i];
if(i + r[i] > R){
R = i + r[i];
mid = i;
}
}
int ans = 0;
RP(i, 1, len)
ans = max(ans, r[i]);
printf("%d", ans - 1);
return 0;
}
Z-algorithm
又稱擴展KMP。可以快速處理出串\(S\)與其所有后綴的最長公共前綴。可以用KMP類似的方法求一個\(\text{nxt}\)數(shù)組,但是更簡單的方法還是利用manacher的思想。
轉載一下原作者的博客鏈接:cosmicAC。
和manacher一樣,設\(r(i)\)表示從\(i\)開始的后綴和原串的最長公共前綴長度。和回文串一樣,當某一個lcp足夠大,足以覆蓋當前擴展點時,我們可以直接從前面繼承答案。設這個lcp的后綴起點為\(t\),和manacher類似,我們可以令\(r(i) = \min(r(l-t+1), t + r(t) - i)\),然后暴力擴展剩余未知的部分,直到找到第一個\(S_{r(i)} \neq S_{i+r(i)}\)的\(r(i)\),然后更新\(t\)。似乎這個\(r(i)\)數(shù)組又稱“\(z\)數(shù)組”,這個算法才得名Z-algorithm。
如何求文本串\(S\)與模式串\(T\)的各后綴的lcp?只需要把\(T\)與一個分隔符\(\Lambda\)與文本串\(S\)按順序連接成\(T + \Lambda + S\),再求\(T + \Lambda + S\)的\(r(i)\)數(shù)組即可。答案為從分隔符后開始的\(r(i)\)。
另外,掃描要注意直接從\(1\)而不是\(0\)開始,原理應該和KMP在自匹配的過程一樣。
int main(){
scanf("%s", S); int Sl = strlen(S);
scanf("%s", T); int Tl = strlen(T);
strcat(C, T), strcat(C, "$"), strcat(C, S);
len = strlen(C);
T[len + 1] = '@';
RP(i, 1, len - 1){
if(i <= r[t] + t)
r[i] = min(r[i - t], r[t] + t - i);
else
r[i] = 0;
while(C[i + r[i]] == C[r[i]])
++ r[i];
if(i + r[i] > t + r[t])
t = i;
}
RP(i, 0, Tl - 1) printf("%d ", i == 0 ? Tl : r[i]);
putchar('\n');
RP(i, Tl + 1, len - 1) printf("%d ", r[i]);
return 0;
}
另外,補充一下這個算法和普通KMP的轉換關系:
if(i + r[i] > t + r[t]){
RP(j, t + r[t], i + r[i] - 1) nxt[j] = j - i + 1;
t = i;
}
Trie
一種特殊的數(shù)據(jù)結構,用于維護若干個單詞。
Trie有一種類似自動機的結構,可以通過字符指針\(p(q, c) = q\prime\)轉移到不同的狀態(tài),并可以標記終態(tài)以標識這個單詞的結尾。
注意一下,Trie的空間復雜度為\(O(|\Sigma|N|S|)\),其中\(N\)為單詞數(shù),\(|\Sigma|\)為字符集大小,\(|S|\)為單詞平均長度。如果沒有算好空間,Trie樹很有可能會MLE。
單次插入單詞和查詢單詞存在性的時間復雜度都是\(O(|S|)\)的。
Trie還有一些神奇的應用。舉個例子:給定一個數(shù)集\(A_i\),求從中選出兩個數(shù),使得兩個數(shù)的異或和最大。最暴力的做法是直接\(O(N^2)\)比較,而通過Trie樹可以做到\(O(N \log A_{\max})\)。通過貪心,對于一個數(shù)\(x\),我們每次嘗試轉移到它的相反位;如果不能轉移,就妥協(xié)走另一邊。比如這道題:最長異或路徑。
AC自動機
本質上是在Trie樹上建立KMP自動機。但怎么建?這是一個大問題。
仔細回憶一下KMP的實現(xiàn)方法:當遇到一個失配位置時,我們需要不斷迭代\(\text{nxt}\)指針,在保證前幾位匹配時,找到盡可能大的\(\text{nxt}\)位置。
回憶一下,KMP\(\text{nxt}(i)\)數(shù)組的含義是“當前子串里,前綴和后綴的最長公共子串”。此時從\(S_1\)走到\(S_{\text{nxt}(i)}\)這個過程,和\(S_{i-\text{nxt}(i)+1}\)走到\(S_{i}\)完全等效。這個性質保證了我每次可以盡可能小地往回跳。
AC自動機同理。\(fail\)指針使得“從某個狀態(tài)轉移到\(q\)狀態(tài)”,和“從根節(jié)點轉移到\(fail(q)\)狀態(tài)”完全等效。這使得我們失配之后有依可循。你可以把\(fail\)指針看成一條\(\varepsilon\)轉移邊,因為它的轉移不需要消耗任何字符。
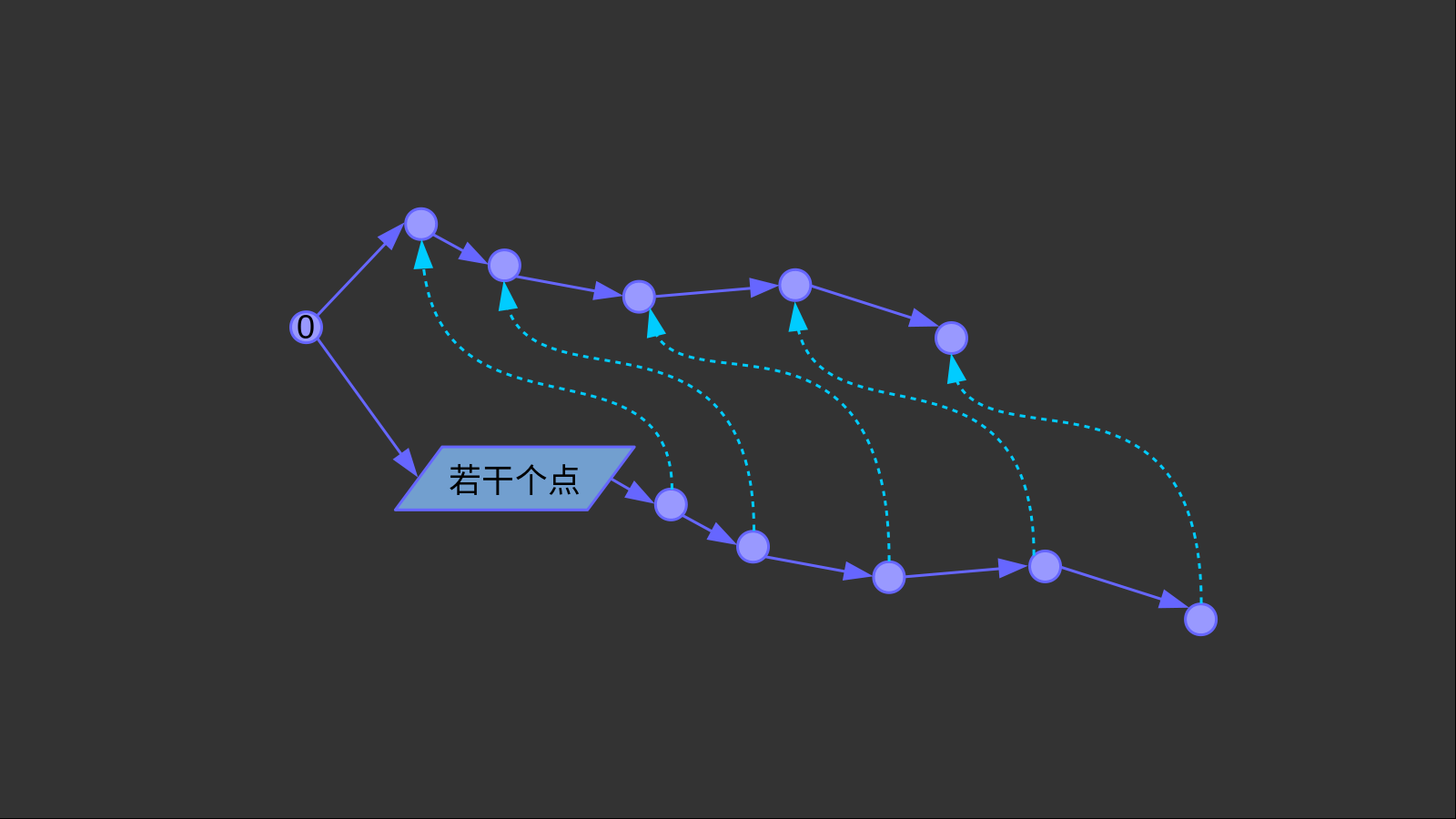
如上圖所示。這兩條紫色的鏈條完全相同,但其中一個直接接在根節(jié)點上,而一個接在若干個點前。此時我們就可以用若干個\(fail\)指針連接兩條鏈。這樣,當當前指針失配時,我們可以隨時跳轉到另一條鏈上。
如何連\(fail\)邊?假設整個trie樹的根節(jié)點為\(0\),那么對于任意一個\(p(0,c)\),它的失配指針只能指向\(0\)。這和KMP算法的初始化是一樣的。
接下來,我們分層進行。對于一個節(jié)點\(u\),如果后繼狀態(tài)\(p(u,c)\)存在,那我們從后繼狀態(tài)連一條“平行”的\(fail\)邊指向另一條鏈,即令\(fail(p(u,c)) = p(fail(u),c)\)。這樣就可以形成向上圖那樣的分層網(wǎng)格的形狀了。
如果\(p(u,c)\)不存在,那么我們直接把這個轉移邊和\(fail(u)\)的轉移邊合并,即令\(p(u,c) = p(fail(u),c)\)。這樣做的好處是可以形成一個\(trie\)圖,從而得以查詢任意長的字符串。
但是,一個trie圖的結構過于復雜。舉個例子,單詞組\(\mathcal{hat},\mathcal{cat},\mathcal{cup}\)的trie圖如下:
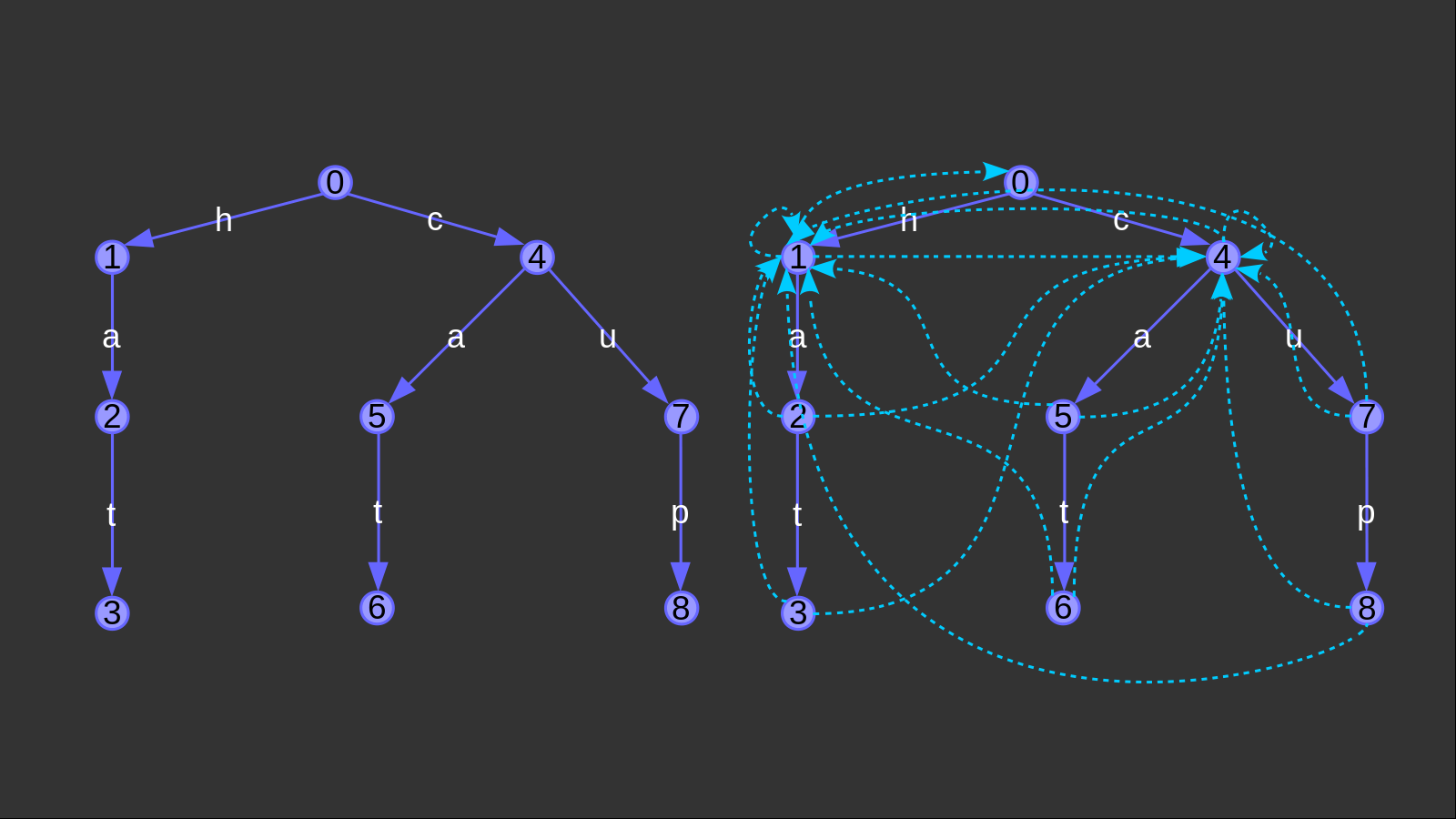
事實上,從每個節(jié)點出發(fā)都有\(26\)條邊可走。青色的邊不是\(fail\)邊(在上例中,\(fail\)是全部指向\(0\)節(jié)點的),而是通過構造\(fail\)邊衍生出來的新的轉移邊。上圖省略了連向\(0\)的點,并且滿足青邊的轉移字符和轉移到這個狀態(tài)的紫邊的轉移字符一致。
int p[maxn][26],leaf[maxn],tot,fail[maxn];
void ins(char *str)
{
int u=0;
int len=strlen(str);
RP(i,0,len-1)
{
int c=str[i]-'a';
if(!p[u][c])
p[u][c]=++tot;
u=p[u][c];
}
++leaf[u];
}
void prefail()
{
RP(i,0,25)
if(p[0][i])
fail[p[0][i]]=0,q.push(p[0][i]);
while(!q.empty())
{
int u=q.front();q.pop();
RP(i,0,25)
{
if(p[u][i])
fail[p[u][i]]=p[fail[u]][i],q.push(p[u][i]);
else
p[u][i]=p[fail[u]][i];
}
}
}
int query(char *str)
{
int len=strlen(str);
int r=0,ans=0;
RP(i,0,len-1)
{
int c=str[i]-'a';
r=p[r][c];
for(register int t=r;t&&~leaf[t];t=fail[t])
ans+=leaf[t],leaf[t]=-1;
}
return ans;
}



 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號