前置知識

• 樹：樹是一個特殊的圖，其邊通常為無向邊，并且一共只有 \(n-1\) 條邊，全圖連通，通常有一個根。如果題目并沒有明確指明某個節(jié)點為根，那么這棵樹就是一棵無根樹，這種情況下一般讓 \(1\) 為根。
• 祖先：在樹上，如果節(jié)點 \(y\) 是節(jié)點 \(x\) 的祖先，當且僅當 \(y\) 出現(xiàn)在從 \(x\) 到根的最短路徑上。特別的，父節(jié)點是一個節(jié)點特殊的祖先節(jié)點。
• ST：一種不支持修改，僅支持查詢操作的東西，耗費 \(O(n\log n)\) 的時間預處理，然后可以 \(O(1)\) 查詢一個區(qū)間的最大值/最小值/最大公因數(shù)等。要求查詢的東西滿足結(jié)合律，并且如出現(xiàn)重疊部分不會錯誤。

最近公共祖先（LCA）是什么？

最近公共祖先，即 Least Common Ancestors，簡稱 LCA，表示樹上兩個節(jié)點 \(x\) 和 \(y\) 分別的祖先節(jié)點合集的交集中最深的節(jié)點。比如說：

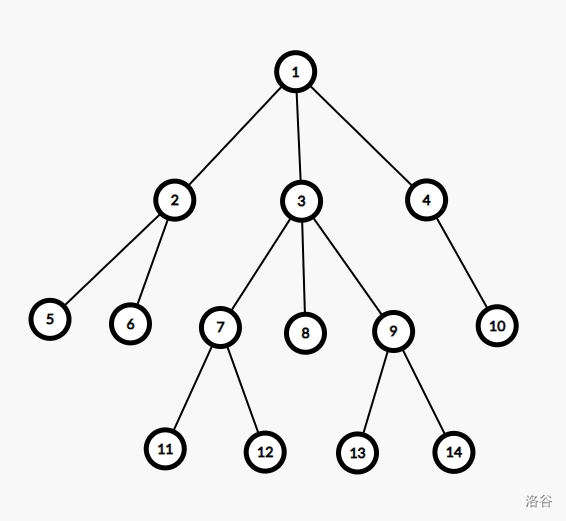
在上圖中，\(LCA(4,6)=1\)，\(LCA(7,14)=3\)，\(LCA(11,12)=7\)。

暴力求解 LCA

求解 LCA，有一種最壞時間復雜度 \(O(n)\) 的求解 LCA 的方案。

首先要進行預處理。以 \(1\) 為根節(jié)點跑一遍 DFS，算出每個節(jié)點的深度，并記錄下每個節(jié)點的父節(jié)點。

void DFS(int u,int Fath){
    dep[u]=dep[Fath]+1,fa[u]=Fath;
    for(int v:g[u])if(v^fa)DFS(v,u);return;
}

這樣我們就 \(O(n)\) 得知了每個節(jié)點的深度 \(dep_u\) 以及每個節(jié)點的父節(jié)點 \(fa_u\)。

接下來就是求解 \(LCA(x,y)\) 了。

首先，我們先要保證 \(x\) 和 \(y\) 的深度相同。

不妨讓 \(dep_x \ge dep_y\)（如果原本 \(dep_x < dep_y\) 那么 swap(x.y)）。接下來我們不停讓 \(x=fa_x\)，直到 \(dep_x=dep_y\)。

if(dep[x]<dep[y])swap(x,y);
while(dep[x]>dep[y])x=fa[x];

接下來就是求解 LCA 了。

由于 \(x\) 和 \(y\) 的深度已經(jīng)相同，所以我們讓 \(x\) 和 \(y\) 不斷一個一個往上跳，直到 \(x=y\)。

while(x!=y)x=fa[x],y=fa[y];

最后返回 \(x\) 即可。

所以整個 LCA 函數(shù)大概是這個樣子：

int LCA(int x,int y){
    if(dep[x]<dep[y])swap(x,y);
    while(dep[x]>dep[y])x=fa[x];
    while(x!=y)x=fa[x],y=fa[y];
    return x;
}

非常簡略，非常易懂。

LCA 這么簡單嗎？當然不是。

如何優(yōu)化暴力 LCA 算法

剛才的 LCA 算法雖然求解一次時間復雜度還能接受，但如果處理 \(Q=10^5\) 這樣的操作，\(n\) 也是 \(10^5\) 級別的，那么時間復雜度就完全爆炸了，不能接受，考慮優(yōu)化。

時間復雜度的瓶頸在于兩個 while 函數(shù)。我們是一個一個跳的，很慢。但如果我們按照 \(\log\) 的時間復雜度來算呢？如果我們每次跳 \(2^k\) 個呢？總之差值肯定是一個整數(shù)，拆成二進制后頂多也就二十來位。這樣不就快多了？

但是處理的東西就復雜些。本來只需要存儲自己的父節(jié)點即可，但現(xiàn)在要存儲自己往上跳 \(2^0,2^1,2^2,\dots,2^k\) 的祖先節(jié)點。看上去很麻煩，這東西好實現(xiàn)嗎？其實上很簡單，這個思想就類似于 ST。只需要在 DFS 過程中，每枚舉到一個節(jié)點 \(u\)，就花費 \(O(\log n)\) 的時間計算存儲一下即可。

那么一開始的預處理（DFS）部分的代碼就變成了這樣：

void DFS(int u,int fa){
    dep[u]=dep[fa]+1,f[u][0]=fa;
    for(int i=0;f[u][i];i++)f[u][i+1]=f[f[u][i]][i];
    for(int v:g[u])if(v^fa)DFS(v,u);return;
}

其中 \(f_{i,u}\) 表示節(jié)點 \(u\) 往上跳 \(i\) 步后所處節(jié)點。如果跳爆了（樹沒有那么大）那么值為 \(0\)。

那么 LCA 求解過程中的兩個 while 函數(shù)的時間復雜度就都可以得到改善啦！從 \(O(n)\) 一下變?yōu)?\(O(\log n)\)，很爽吧？

具體來說，就是利用 \(f\) 數(shù)組來跳躍。

細節(jié)見代碼吧。

int LCA(int u,int v){
    if(dep[u]>dep[v])swap(u,v);
    for(int i=20;i>=0;i--)
        if(dep[u]<=dep[v]-(1<<i))v=f[v][i];
    if(u==v)return u;
    for(int i=20;i>=0;i--)
        if(f[u][i]!=f[v][i])u=f[u][i],v=f[v][i];
    return f[u][0];
}

這樣就快多了。不是嗎？

然后你就可以把這些碎片代碼組裝起來，加上 main 函數(shù)，通過模板題了。

例題選講

例 \(1\)

樹上前綴和。簡單題。

具體來說就是一開始 DFS 的時候加一個 \(s\) 數(shù)組，每次 \(s_u = s_{fa} + a_u\)。

然后計算 \(x\) 到 \(y\) 的路徑時就直接 \(s_x + s_y - 2 \times s_{LCA(x,y)} + a_{LCA(x,y)}\) 即可。

注意特判一下 \(x=y\) 的情況——直接輸出 \(a_x\) 即可。

代碼是十萬年以前寫的，很丑。就不貼了。

例 \(2\)

樹上差分。簡單題。

這完全是板子樹上差分啊喂！

就是說，你還是要維護一個 \(d\) 數(shù)組，然后差分的時候需要推一推式子。

在本題中，你只需要：

int x,y,lca;cin>>x>>y;lca=LCA(x,y);
d[x]++,d[y]++,d[lca]--,d[f[lca][0]]--;

即可。

然后最后跑一遍，恢復一下就行。

void CNT(int u,int fa){
    for(int v:g[u])
        if(v^fa)CNT(v,u),d[u]+=d[v];
    ans=max(ans,d[u]);return;
}

輸出 \(ans\) 即可。

總結(jié)

LCA 兩大特色，一個樹上差分，一個樹上前綴和。相比于后者，前者的應用要更廣泛一些。

很多時候 LCA 也會用來輔助各種東西。

究其根源，LCA 就是用來計算樹上兩個節(jié)點的路徑的長度的！當然啦，LCA 也很聰明，它支持存在邊權(quán)/點權(quán)之類的附屬條件的樹哦！

這就是 LCA，圖論中的好伙伴！