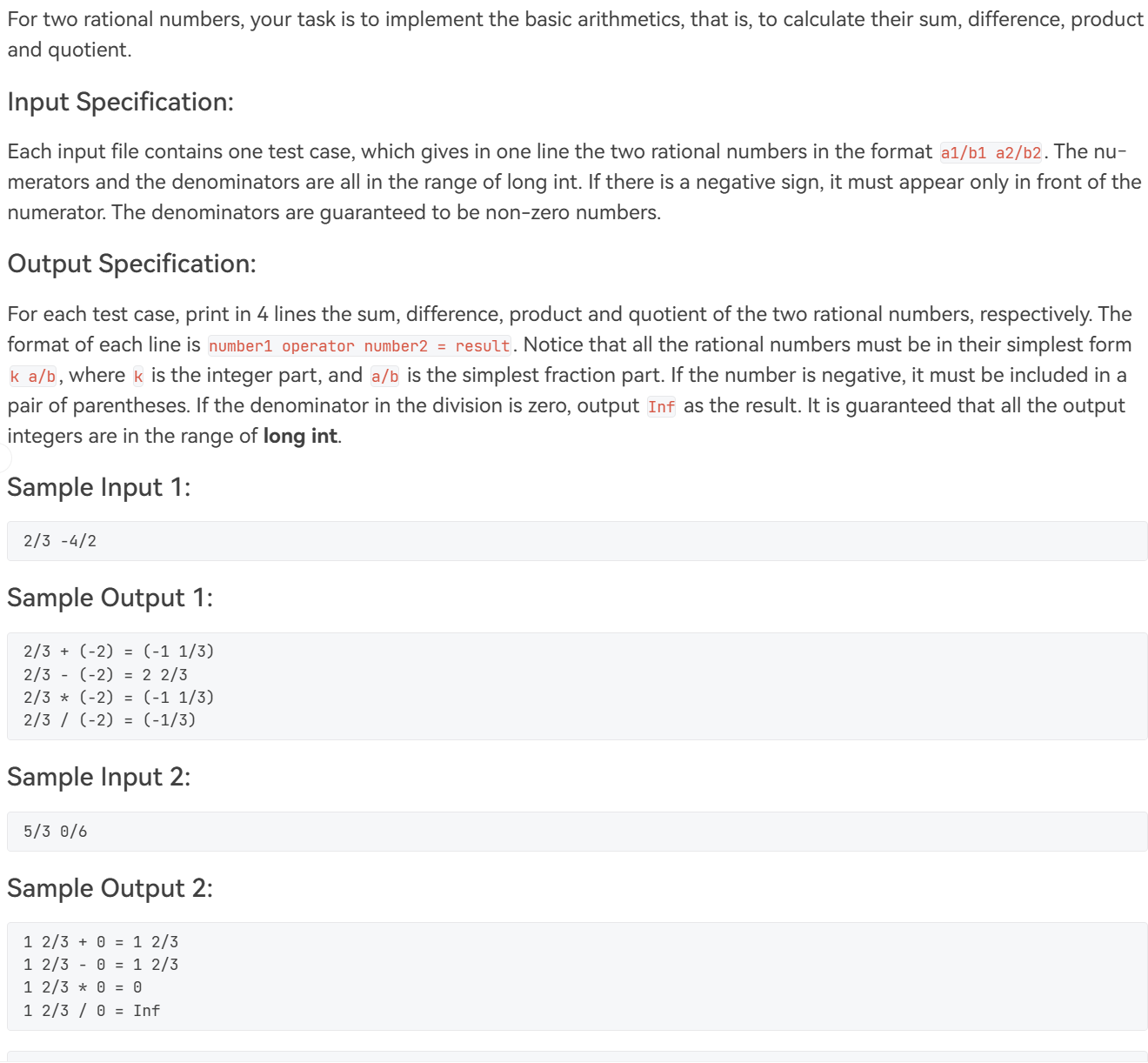
題目
![]()
解法1
點擊查看代碼
#include<iostream>
#include<cmath>
using namespace std;
struct Fraction {
long long num, den;
Fraction(long long n = 0, long long d = 1) {
if (d < 0) {
n = -n;
d = -d;
}
long long g = gcd(abs(n), d);
num = n / g;
den = d / g;
}
// 最大公約數
long long gcd(long long a, long long b) {
return b == 0 ? a : gcd(b, a % b);
}
// 加減乘除,運算符重載
Fraction operator+(const Fraction& f) {
return Fraction(num * f.den + f.num * den, den * f.den);
}
Fraction operator-(const Fraction& f) {
return Fraction(num * f.den - f.num * den, den * f.den);
}
Fraction operator*(const Fraction& f) {
return Fraction(num * f.num, den * f.den);
}
Fraction operator/(const Fraction& f) {
if (f.num == 0) return Fraction(1, 0); // 用 1/0 表示 Inf
return Fraction(num * f.den, den * f.num);
}
// 轉換成字符串
string to_string() const {
if (den == 0) return "Inf";
long long n = num, d = den;
bool neg = n < 0;
n = abs(n);
long long int_part = n / d;
long long rem = n % d;
string result;
if (neg) result += "(-";
if (int_part != 0) result += std::to_string(int_part);
if (int_part != 0 && rem != 0) result += " ";
if (rem != 0) result += std::to_string(rem) + "/" + std::to_string(d);
if (int_part == 0 && rem == 0) result += "0";
if (neg) result += ")";
return result;
}
};
int main() {
long long a1, b1, a2, b2;
scanf("%lld/%lld %lld/%lld", &a1, &b1, &a2, &b2);
Fraction f1(a1, b1), f2(a2, b2);
string s1 = f1.to_string();
string s2 = f2.to_string();
cout << s1 << " + " << s2 << " = " << (f1 + f2).to_string() << endl;
cout << s1 << " - " << s2 << " = " << (f1 - f2).to_string() << endl;
cout << s1 << " * " << s2 << " = " << (f1 * f2).to_string() << endl;
cout << s1 << " / " << s2 << " = " << (f1 / f2).to_string() << endl;
return 0;
}


 浙公網安備 33010602011771號
浙公網安備 33010602011771號