本文針對力扣的算法題“相交鏈表”，提供了四種不同的算法解決思路，詳細介紹了其中的雙指針法和數學法的算法步驟和 Java 代碼。

題目：給你兩個單鏈表的頭節點 headA 和 headB ，請你找出并返回兩個單鏈表相交的起始節點。如果兩個鏈表不存在相交節點，返回 null 。題目數據 保證 整個鏈式結構中不存在環。注意，函數返回結果后，鏈表必須 保持其原始結構 。

---

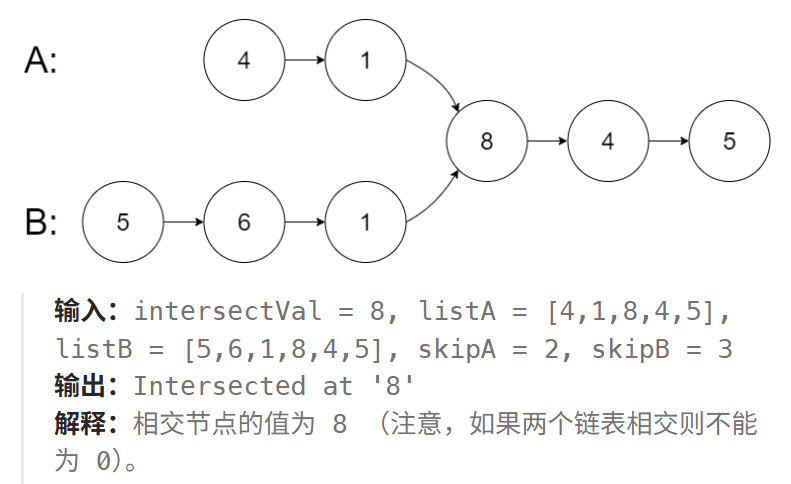
有幾種不同的算法思路解決這道算法：

1. 雙指針法：

• 使用兩個指針分別遍歷兩個鏈表，如果兩個鏈表相交，那么這兩個指針最終會在相交點相遇；如果兩個鏈表不相交，那么這兩個指針最終都會到達各自鏈表的末尾（即 null）。

• 時間復雜度是 O(m + n)，空間復雜度是 O(1)，其中 m 和 n 分別是兩個鏈表的長度，因為最多遍歷每個鏈表兩次。

2. 哈希表法：

• 遍歷其中一個鏈表，將所有節點存儲在哈希表中。

• 遍歷另一個鏈表，檢查每個節點是否在哈希表中。

• 時間復雜度：O(m + n)，空間復雜度：O(m)，其中 m 和 n 分別是兩個鏈表的長度。

3. 數學法：

• 計算兩個鏈表的長度，然后讓較長的鏈表先移動到與較短的鏈表長度相同的位置，再同時遍歷兩個鏈表。

• 時間復雜度：O(m + n)，空間復雜度：O(1)。

4. 遞歸法：

• 使用遞歸遍歷兩個鏈表，直到找到相交點或到達鏈表末尾。

• 時間復雜度：O(m + n)，空間復雜度：O(h)，其中 h 是遞歸深度。

由于雙指針法和數學法不需要使用額外的空間，空間復雜度是O(1)，所以我采用雙指針法和數學法解決這道題目，下面給出這兩個方法的具體步驟和代碼。

一、雙指針法

算法步驟：

1. 初始化兩個指針：分別指向兩個鏈表的頭節點 headA 和 headB。

2. 遍歷鏈表：同時遍歷兩個鏈表，直到兩個指針都到達 null。

3. 指針重置：如果兩個指針都到達了 null，則說明兩個鏈表不相交，返回 null。否則，將兩個指針重置到對方的鏈表頭節點。

4. 再次遍歷：再次同時遍歷兩個鏈表，這次如果兩個鏈表相交，兩個指針將在相交點相遇；如果不相交，兩個指針最終都會到達 null。

5. 返回結果：如果兩個指針相遇，返回相遇的節點；否則返回 null。

Java 代碼：

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode pointerA = headA;
        ListNode pointerB = headB;

        while (pointerA != pointerB) {
            pointerA = (pointerA == null) ? headB : pointerA.next;
            pointerB = (pointerB == null) ? headA : pointerB.next;
        }

        return pointerA; // 當兩個指針相遇時，返回相遇的節點
    }
}

二、數學法

算法步驟：

1. 計算長度：分別計算兩個鏈表的長度。

2. 找齊頭尾：讓較長的鏈表先移動，使其頭指針與較短的鏈表頭指針相距相同的步數。

3. 同時遍歷：從兩個鏈表的頭指針開始，同時遍歷兩個鏈表，如果兩個鏈表相交，那么這兩個指針最終會在相交點相遇；如果不相交，那么兩個指針最終都會到達 null。

Java 代碼：

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }

        // 計算兩個鏈表的長度
        int lenA = 0, lenB = 0;
        ListNode tmpA = headA, tmpB = headB;
        while (tmpA != null) {
            lenA++;
            tmpA = tmpA.next;
        }
        while (tmpB != null) {
            lenB++;
            tmpB = tmpB.next;
        }

        // 讓較長的鏈表先移動，使其頭指針與較短的鏈表頭指針相距相同的步數
        while (lenA > lenB) {
            headA = headA.next;
            lenA--;
        }
        while (lenB > lenA) {
            headB = headB.next;
            lenB--;
        }

        // 從兩個鏈表的頭指針開始，同時遍歷兩個鏈表
        while (headA != null && headA != headB) {
            headA = headA.next;
            headB = headB.next;
        }

        // 如果兩個鏈表相交，返回相交的節點；否則返回null
        return headA;
    }
}