Impulse Noise（圖像脈沖噪音）的抑制和處理方法（提取自《現代圖像處理算法教程》一書并做解釋）。

　　相關參考文章：現代圖像處理算法教程（全）

　　參考書籍：modern-algorithms-for-image-processing-computer-imagery-by-example-using-C#

　　在上面的英文版書籍中，提出了一種去除脈沖噪音的方法，所謂的脈沖噪聲是影響單個的、隨機選擇的像素或相鄰像素的組合，而不是影響圖像的所有像素（這個是高斯噪聲的特征）。我們傳統概念中提到的椒鹽噪音其實只是脈沖噪音的一種特例，脈沖噪音可以分暗脈沖噪聲和亮脈沖噪聲。暗噪聲包含亮度低于其鄰域亮度的像素或像素組，而亮噪聲則相反。

　　抑制灰度或彩色圖像中的脈沖噪聲的問題相當復雜，我們以暗噪聲為例，則需要自動檢測圖像中滿足以下條件的像素的所有子集 S :

　　1、子集 S 的所有像素必須具有低于或等于閾值 T 的亮度。

　　2、子集 S 中的所有像素必須是連接在一起的。

　　3、像素數（即 S 的面積）低于預定值 M 。

　　4、不屬于 S 但是與 S 的相鄰的所有像素必須具有高于 T 的亮度。

　　5、對于不同的子集 S ，閾值 T 可以不同。

　　這個問題很難，因為閾值 T 是未知的。理論上，在一個接一個地測試 T 的所有可能值的同時解決問題是可能的。然而，這樣的算法會非常慢。

　　M. I. Schlesinger 在1997年提出了以下快速解決方案的想法:

　　　“We propose such a procedure that the “noise removing” with subsequent thresholding gives the same results as thresholding with subsequent commonly used noise removing in the binary picture. This equivalency holds for every threshold’s value.

　　我感覺到難以翻譯，就直接用原文把。

　　接著書本里提出了一個具體的算法，我先不說具體的實現，我把我寫完算法后對該算法的理解先用文字表達出其核心的思想。

　　以暗脈沖噪音為例，其實現的方法為：

　　對圖像的所有像素，先從亮度高的像素開始，依次尋找該像素周邊領域里亮度小于或等于該像素的連續區域，如果這個區域的面積小于預設的面積M，則把這個區域內的所有像素都設置為和這個領域像素相接觸的所有像素中的最小值，顯然，這個最小值也要比這個區域內的任何像素都亮。處理完亮度最高的像素后，在繼續處理后續亮度逐漸降低的像素，不但重復這個過程，直到所有像素都處理完成。

　　對于亮脈沖噪音，則處理過程相反。

　　因此，整個過程只有一個外部參數，即預設的面積，當然，暗脈沖噪音和亮脈沖噪音對應的預設面積可以不同。

　　從以上的過程來看，所謂的暗脈沖噪音，噪音部位并不一定是很暗的像素，只是相對來說暗一點，比如一團像素值為253的像素如果周邊都是255，則只要他的面積小于M，也就會被賦值為255。這個和我們傳統的直觀理解還是有所不同的，這也是為什么我們去除暗脈沖噪音時為什么要從最亮的像素開始向暗像素逐步進行處理。

　　從上述過程來看，如果直接實現這樣的定義，則還是個非常耗時的過程，因為

　　（1）、需要從255每次遞減一直到0為止，256次遍歷整個圖像，每次遍歷時尋找到像素值等于循環變量的像素位置，然后在該位置進行符合條件的連續區域查找。

　　（2）、連續區域查找本身是個較為復雜的過程，也是相當耗時。

　　（3）、如果不進行256次遍歷，則需要對圖像像素進行排序，而且排序時還要帶上圖像坐標的X和Y信息。對于大圖，排序本身也是非常耗時的。

　　因此，文章中提出了幾個供加速的過程，也是非常有意義的事情。

　　（1）為了避免排序或者256次遞歸，首先利用直方圖的有關屬性，并定義了一個二維數組，來保存圖像中各個色階像素的有關信息，二維數組的第一維范圍從0到255，表示色階值或者說亮度值，第二維的范圍是動態的，其大小是圖像中具有該色階或亮度像素的個數，這樣，比如數組Index[light][10]是表示亮度等于light的所有像素的集合中的第十個像素的索引（或者位置信息），因此，可以明顯的看到這個數組的第二維的里所有元素相加的總和即為圖像的像素個數。

　　這樣，當從小亮度開始讀取數組Index時（第一維），我們獲得以亮度增加的順序排序的像素的索引，但是當以相反的方向讀取時，我們獲得以亮度減少的順序排序的像素的索引。

　　那個書中的C#代碼寫的比較混亂，我貼一段C++的代碼表示下上述過程的意思：

//    計算圖像的直方圖，從而間接獲取每個色階在圖像中的像素數
    for (int Y = 0; Y < Height; Y++)
    {
        unsigned char* LinePS = Src + Y * Stride;
        for (int X = 0; X < Width; X++)
        {
            Histgram[LinePS[X]]++;
        }
    }
    //    為每個色階分配合適的內存
    for (int Y = 0; Y < 256; Y++)
    {
        if (Histgram[Y] == 0)
        {
            PosIndex[Y] = NULL;
        }
        else
        {
            //    根據每個色階的像素數分配合適的大小
            PosIndex[Y] = (Point*)malloc(Histgram[Y] * sizeof(Point));
            if (PosIndex[Y] == NULL)
            {
                Status = IM_STATUS_OUTOFMEMORY;
                goto FreeMemory;
            }
        }
    }

    //    再次把直方圖數據賦值為0，讓其充當在循環中的計數器，并且最終也恢復成正確的直方圖數據
    memset(Histgram, 0, 256 * sizeof(int));

    for (int Y = 0; Y < Height; Y++)
    {
        unsigned char* LinePS = Src + Y * Stride;
        for (int X = 0; X < Width; X++)
        {
            int Light = LinePS[X];
            //    第一個索引Light表示色階，第二個Histgram[Light]表示在Light色階中對應的順序
            //    PosIndex[100][2]則就記錄了圖像中第三個色階值為100的像素的位置，當然這個排序的順序是按照先行后列的
            Point* P = &PosIndex[Light][Histgram[Light]];
            P->X = X;
            P->Y = Y;
            //    這個亮度的索引增加1
            Histgram[Light]++;
        }
    }

　　首先遍歷一次圖像進行直方圖統計，這樣就能知道圖像中每個色階像素的個數，然后根據這個個數分配合理的內存，并再次遍歷圖像，根據每個位置的色階把對應的位置信息填充到二維數組中（或者二維指針）。這樣就記錄了圖像中不同色階的位置信息，并具有一定的統計和排序意義。

　　（2）、為了避免不必要的計算，我們接著計算下圖像的實際最大值和最小值。這個可以直接借用直方圖實現。

    //    求取圖像的最大值和最小值
    int MinValue = 255, MaxValue = 0;
    for (int Y = 0; Y < 256; Y++)
    {
        if (Histgram[Y] != 0)
        {
            MinValue = Y;
            break;
        }
    }
    for (int Y = 255; Y >= 0; Y--)
    {
        if (Histgram[Y] != 0)
        {
            MaxValue = Y;
            break;
        }
    }

　　（3）、接下來就是關鍵了，我們以處理暗脈沖噪音為例，借助前面的處理步驟，我們能輕松的從最亮的像素開始向暗像素開始處理：

//    去除暗噪音，從最大值減開始循環
for (int Light = MaxValue; Light >= MinValue; Light--)
{
    //    掃描所有原圖中像素值等于Light的所有像素位置
    //    Histgram[Light]為0的像素則直接會不進行循環的
    for (int Y = 0; Y < Histgram[Light]; Y++)
    {
        Point* P = &PosIndex[Light][Y];
        int Pos = P->Y * Stride + P->X;
        //......................
    }
}

　　最外一重循環的意思很明顯，而第二重Y循環，從下標0開始，一直到Histgram[Light] - 1，因為Histgram[Light]中實際保存的就是圖像中色階為Light的像素的總個數，在PosIndex[Light][Y]中在保存了各個色階為Light像素的坐標位置。

　　那么在這個循環內部，可以參考書本中的BreadthFirst_D函數，核心就是以當前點為種子點，按照領域的像素小于等于Light的原則進行區域生長，在生長的過程中，如果遇到了大于Light的領域信息，則要用一個變量記錄下這些區域的最小值Min，當生長過程中，發現生長的區域面積已經大于預設值M了，則可以立即停止生長了。否則繼續下去，直到周邊沒有任何像素能繼續生長了。

　　這個生長的過程可以用隊列方便的視線，當然也有數組的方式實現的。 

　　對一個像素生長完成后，如果區域面積是滿足小于M的要求的，則用前面記錄的M值把這些區域的像素都賦值為M，實現噪音的去除。如果大于M了，則可以不管他，繼續下一步處理。

　　但是作者在這里做了一個特別的處理，即區域面積大于M時，我們可以額外多做一個判斷，即在這個區域里如果有和Light值相同的像素，則標記相同像素的那個位置，并且下一次處理那個位置時檢查這個標記，如果已經有了值，則跳過這個像素不處理，這樣就能節省大量的時間，這是因為，如果在同一個聯通區域里的兩個點，具有相同的色階值，則分別以他們為中心進行區域生長時的結果肯定是一模一樣的，因此，后面就完全沒有必要再次進行重復的生長了。

　　書本作者提供的代碼BreadthFirst_D函數里面用了一系列的位操作技巧，個人感覺有點炫技的嫌疑，直接用標記數組起來方便多了。

　　對于彩色圖像，這個算法是不能分通道處理的，因為單獨通道處理可能導致每個點的通道不會被同樣處理，結果就是會出現一些異常的彩色斑點，一般都是用各個彩色像素的灰度信息來作為特征進行計算，然后統一處理三通道數據。

　　我們在理解書本原理的基礎上，自行進行了C++編碼，并對書本提供的兩個圖片進行了測試，均取得了不錯的結果：

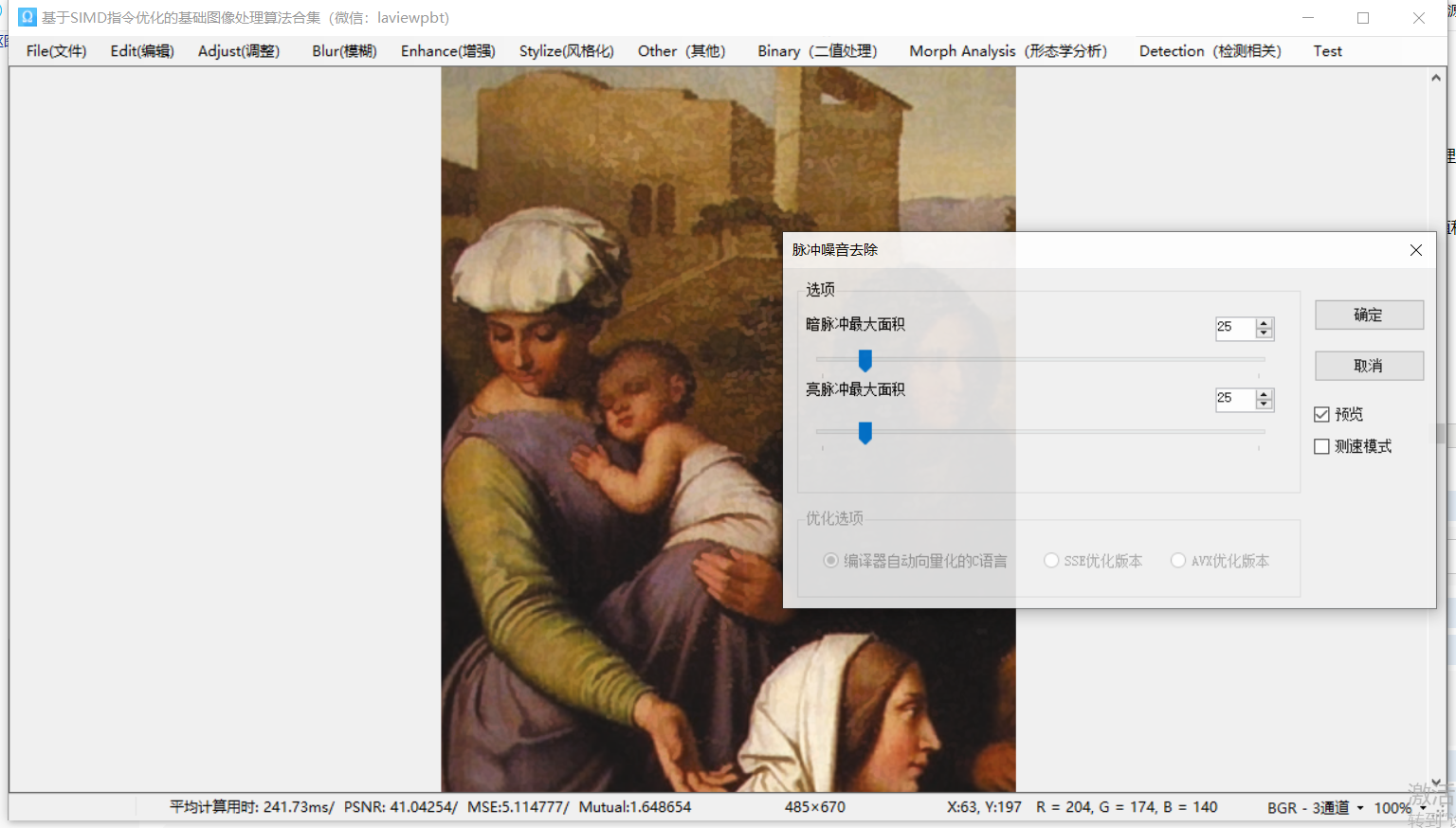
　　一幅灰度圖像，一幅彩色圖像，暗脈沖和亮脈沖的大小都設置為25像素，右圖為去燥后的處理結果，從結果看，非常有效的去除了一些瑕疵，而且，較為關鍵的一點是，基本上我目前研究過的其他的傳統的去燥算法，似乎都達不到類似的較為完美結果。

　　對于典型的椒鹽噪音，因為他本身就屬于脈沖噪音，因此，肯定是能完美出來好的， 如下面兩圖所示:

 　　需要說明的是，即使是這樣做了優化，這個去除噪音的速度呢還是不很很快，而且速度除了和圖像大小有關外，還和圖像的內容有關，也就是說同一樣大小的一幅圖，處理速度可能會有幾倍的差異。

　　另外，在填充這一塊也有一些內容值得考慮，目前是使用領域邊緣中最小的值或最大的值填充整個符合條件的領域，那是否可以考慮用領域邊緣的平均值呢，或者用這個值和領域內的圖像做個融合呢，這樣就可以適當的保留領域內的一些邊緣信息，而不是都變為同一個值。

　　這個算法本身不算什么驚艷或者高深算法，但是這種處理的方式和方法和一般的圖像處理步驟還是有較大的區別的，也可以說是獨樹一幟吧。也許這種思路也可以擴展到一些其他的算法應用中去。 

　　該算法目前也已經集成到我的SSE優化的算法集合里：https://files.cnblogs.com/files/Imageshop/SSE_Optimization_Demo.rar?t=1660121429

　　如果想時刻關注本人的最新文章，也可關注公眾號：