概述

對于兩個點集 \(A,B\) 來說，把其中的每一個點都看做是對應(yīng)向量，則這兩個集合的閔可夫斯基和定義為 \(C=\{ a+b|a\in A,b\in B \}\)。

凸包的閔可夫斯基和

考慮 \(C\) 為凸包 \(A,B\) 的閔可夫斯基和，那么 \(C\) 的大小應(yīng)該為 \(|A||B|\)，但是如果考慮 \(C\) 的凸包，那么點數(shù)應(yīng)該是 \(O(|A|+|B|)\) 的。

如圖：

至于為什么是這樣，我們以上凸殼為例，考慮兩個上凸殼的閔可夫斯基和其實是兩個上凸殼的歸并排序，

如圖：

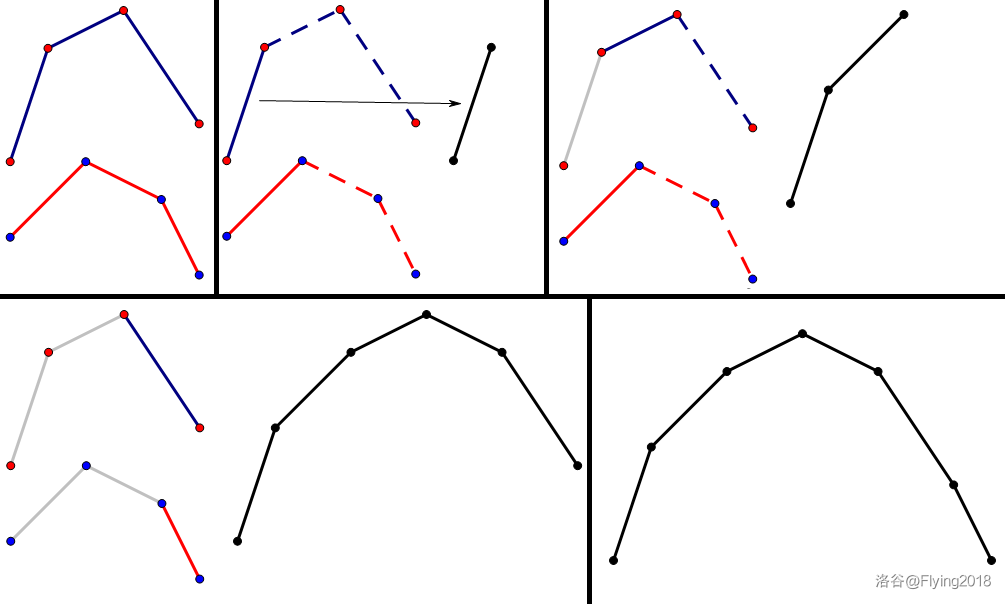
易發(fā)現(xiàn)最終凸包上的邊都是原來的邊，這一點就足以充分說明上面的結(jié)論。

所以兩個凸包的閔可夫斯基和可以做到 \(O(size)\)。利用類似歸并排序即可。具體實現(xiàn)中，我們考慮用一個數(shù)組表示一個凸殼，\(a_i\) 表示橫坐標(biāo)為 \(i\) 時凸殼上對應(yīng)點的縱坐標(biāo)。

注意到一個凸殼相當(dāng)于是若干一次函數(shù)的復(fù)合，則兩個上凸殼的合并相當(dāng)于它們做 \((\max,+)\) 卷積，即加起來的結(jié)果取 \(\max\)。這是因為我們考慮 \((\max,+)\) 卷積的形式：

如果把 \(i,j\) 看做橫坐標(biāo)，把 \(a_i,b_j\) 看做兩個凸殼的縱坐標(biāo)，那么這和 \(C=A+B\) 的定義不謀而合，在 \(C\) 中選的那些最優(yōu)的點一定構(gòu)成一個凸殼，而這個凸殼就是我們合并得到的凸殼。

同樣的，取 \(\min\) 就是做 \((\min,+)\) 卷積。

閔可夫斯基和與 wqs 二分

wqs 二分可以在 \(O(n\log n)\) 的時間復(fù)雜度內(nèi)求出某一個點值的最優(yōu)值，但是如果我們的詢問變成所有的橫坐標(biāo)，該怎么做？

考慮 wqs 二分的一個經(jīng)典問題：給定長度為 \(n\) 的序列 \(a_i\)，要求對于每個 \(k=1,2,\cdots,n\)，恰好選出 \(k\) 個不相交的子區(qū)間，最大化所有不相交子區(qū)間內(nèi)權(quán)值和的和。

顯然這個問題可以構(gòu)建一個費(fèi)用流模型，如圖：

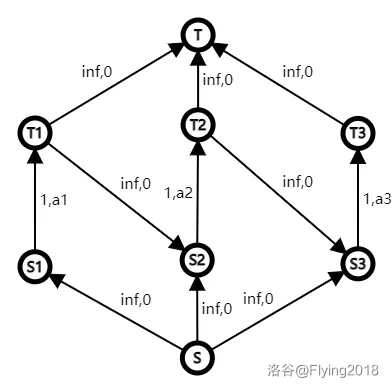
所以這是一個凸函數(shù)，可以用 wqs 二分來解決單個值的問題。考慮加強(qiáng)版的問題。

首先考慮一個 DP，設(shè) \(f_{l,r,k,0/1,0/1}\) 表示 \([l,r]\) 中選 \(k\) 個區(qū)間，左端點有沒有被覆蓋，右端點有沒有被覆蓋。加上后兩維的原因是可以合并相鄰的兩個區(qū)間。

考慮這個函數(shù)顯然關(guān)于 \(k\) 是一個凸函數(shù)，所以我們?nèi)我馊ヒ粋€分界點，總可以在 \(r-l\) 的時間內(nèi)求出。考慮閔可夫斯基和類似于歸并，我們可以取分界點為區(qū)間中點，類似分治，求出答案。