此分類用于記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下：

1. 原課程視頻鏈接：[雙語字幕]吳恩達深度學習deeplearning.ai
2. github課程資料，含課件與筆記:吳恩達深度學習教學資料
3. 課程配套練習（中英）與答案：吳恩達深度學習課后習題與答案

本篇為第一課第二周，在2.1之前的的基礎補充。

本周的課程以邏輯回歸為例詳細介紹了神經網絡的運行，傳播等過程，其中涉及大量機器學習的基礎知識和部分數學原理，如沒有一定的相關基礎，理解會較為困難。
因為，筆記并不直接復述視頻原理，而是從基礎開始，盡可能地創造一個較為絲滑的理解過程。

1.回歸

1.1什么是回歸？

首先依舊擺一個定義:

回歸（Regression）是統計學和機器學習中的一種方法，用于建立自變量（輸入特征）與因變量（輸出目標）之間的關系。回歸的目的是通過分析數據，找出輸入與輸出之間的函數關系，并且根據這個關系來預測連續型的輸出值,回歸模型的主要目標是預測連續變量。

簡單來說，回歸就是通過數據得到輸入輸出間的關系，再根據這個關系為輸入預測連續型的輸出。
之前在第一周中提到的用數據預測房價,就是回歸問題。

之所以一直在強調輸出的連續型，是為了和另一類問題：分類問題作區分，我們會在之后再展開，總之，回歸問題得到的最終結果一定是一個連續的數值，如價格，身高，重量等，而非一類標簽，如是或否等。

1.2 怎么回歸？

我們現在知道了回歸實現的效果，那如何實現回歸呢？即輸入輸出的關系怎么得到的？
簡單來說，就是通過輸入輸出得到擬合函數：

擬合函數可以是線性函數，多項式函數，分段函數等等，我們先忽略語境舉一個最簡單的例子：

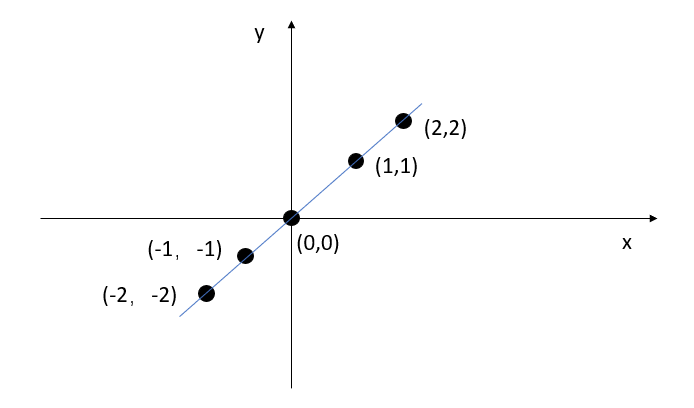
如圖所示，假設我們的數據即為圖中點，我們觀察數據，直接得到擬合關系：

我們通過把輸入代入擬合函數，即可預測其他輸入的輸出：輸入5，輸出5；輸入1.2得到1.2.

1.3 線性回歸

線性回歸可以說是最簡單的回歸算法，剛剛的 \(y=x\) 就是最簡單的線性回歸，線性回歸得到的擬合函數圖像一定是一條直線。
線性回歸的通式如下：

其中，在數學上，\(w\) 被稱為斜率，\(b\) 被稱為截距。
但在機器學習與神經網絡的背景下，二者通常有更切實的稱呼。

1. \(w\)（權重）： 對輸入特征的加權系數，表示輸入在網絡中的重要性。
2. \(b\) （偏置）：模型的“起始點”或“偏移量，作用是調整每個神經元的輸出。

了解了基礎的概念后，我們說回剛剛的例子：
假設在該題的語境下，所以的數據都完美滿足了\(y=x\) 這一擬合函數，實現了絕對精準的預測。
那就是說，我們只用線性回歸就實現了對該問題的完美解，但可惜的是，當我們引進現實的情境后，這幾乎是不可能做到的。

我們回顧一下最開始的房價預測的例子：

當時我們通過給神經網絡的隱藏層增加ReLU激活函數來解決了房屋價格和面積的都不可能為負的情況，可現在再觀察，我們發現圖里的分段線性擬合函數最多只能預測到一個大致的范圍。
結合現實我們也知道，影響房屋價格的因素復雜的，我們不能用線性回歸來精準的預測房屋價格，這便需要更復雜的回歸算法，如其他機器學習算法或者神經網絡。
而評價一個算法的好壞，首先便要看該算法在要解決問題的數據上的表現。
這便涉及到了更具體的評價指標，我們在之后遇到后再展開。

通過本篇，可以解了關于回歸的一些基本知識，而知道了這些基礎后，便可以比較通暢的學習2.1及之后的內容。