數據結構與算法（1）數據組織方式、空間利用率、算法的重要性——ZJU

1.1數據結構基本概念

1.1.1解決問題方法的效率， 跟數據的組織方式有關

思考問題：如何在書架上擺放圖書？

不同的擺放方法（即數據的組織方式），影響著插入新圖書與查找圖書的效率（即解決問題方法的效率），例如，亂放與按類歸類后按字母順序排列。

故有：解決問題方法的效率， 跟數據的組織方式有關

1.1.2解決問題方法的效率， 跟空間的利用效率有關

循環法與遞歸法實現例子

例2：寫程序實現一個函數PrintN，使得
傳入一個正整數為N的參數后，能順序
打印從1到N的全部正整數

循環法：

void PrintN ( int N )
{ int i;
for ( i=1; i<=N; i++ ){
printf(“%d\n”, i );
}
return;
}

遞歸法：

void PrintN ( int N )
{ if ( N ){//N!=0時進行遞歸調用，N==0時直接返回，故打印時從1開始
PrintN( N – 1 ); 
printf(“%d\n”, N );
}
return;
} 

運行后會發現遞歸法并不能滿足要求，直接跳出（吃內存），循環法正常運行。

故有：解決問題方法的效率， 跟空間的利用效率有關

1.1.3解決問題方法的效率， 跟算法的巧妙程度有關

冪指數多項式求和——循環累次相加和秦九韶算法

寫程序計算給定多項式在給定點x
處的值

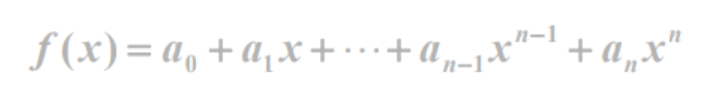
//循環累次相加:

double f( int n, double a[], double x )
{ int i;
double p = a[0];
for ( i=1; i<=n; i++ )
p += (a[i] * pow(x, i)); 
return p;
} 

//秦九韶算法:

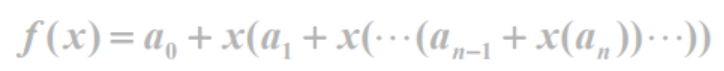
double f( int n, double a[], double x )
{ int i;
double p = a[n];
for ( i=n; i>0; i-- )
p = a[i-1] + x*p;
return p;
} 

兩者的運行時間是不相同的，進行運行測試：

其中注意幾點：

1. 使用clock()進行時鐘計時

   clock()：捕捉從程序開始運行到clock()被調用時所耗費的時間。這個
   時間單位是clock tick，即“時鐘打點”。
   //其中常數CLK_TCK(或CLOCKS_PER_SEC)：機器時鐘每秒所走的時鐘打點數
   

2. 當運行程序的時間太短但必須要進行計時時，可以重復運行N次（循環），測算時間后/N。

普通的運行一次計時程序：

#include <stdio.h>
#include <time.h>
clock_t start, stop;/* clock_t是clock()函數返回的變量類型 */
double duration;/* 記錄被測函數運行時間，以秒為單位 */
int main ()
{ /* 不在測試范圍內的準備工作寫在clock()調用之前*/
start = clock(); /* 開始計時 */
MyFunction(); /* 把被測函數加在這里 */
stop = clock(); /* 停止計時 */
duration = ((double)(stop - start))/CLK_TCK;
    /* 計算運行時間 */
    /* 其他不在測試范圍的處理寫在后面，例如輸出duration的值 */
return 0;
} 

添加了重復運行后的實現程序：

#include <stdio.h>
#include <time.h>
#include <math.h>
define MAXK 1e7 /* 被測函數最大重復調用次數 */
clock_t start, stop; 
double duration;
#define MAXN 10 /* 多項式最大項數，即多項式階數+1 */
double f1( int n, double a[], double x );
double f2( int n, double a[], double x );
int main ()
{ int i;
double a[MAXN]; /* 存儲多項式的系數 */
for ( i=0; i<MAXN; i++ ) a[i] = (double)i; 
start = clock();
for ( i=0; i<MAXK; i++ ) /* 重復調用函數以獲得充分多的時鐘打點數*/
	f1(MAXN-1, a, 1.1);
stop = clock();
duration = ((double)(stop - start))/CLK_TCK/MAXK; 
printf("ticks1 = %f\n", (double)(stop - start));
printf("duration1 = %6.2e\n", duration);
start = clock();
for ( i=0; i<MAXK; i++ ) /* 重復調用函數以獲得充分多的時鐘打點數*/
	f2(MAXN-1, a, 1.1); 
stop = clock();
duration = ((double)(stop - start))/CLK_TCK/MAXK; 
printf("ticks2 = %f\n", (double)(stop - start));
printf("duration2 = %6.2e\n", duration);
return 0
}

故有：解決問題方法的效率， 跟算法的巧妙程度有關

1.1.4抽象數據類型（Abstract Data Type ）

• 數據類型

  ? 數據對象集

  ? 數據集合相關聯的操作集

  （可能面向對象的編程語言更容易理解。）

• 抽象：描述數據類型的方法不依賴于具體實現

? 與存放數據的機器無關

? 與數據存儲的物理結構無關

? 與實現操作的算法和編程語言均無關

只描述數據對象集和相關操作集 “是什么 ”，并不涉及 “如何做到 ”的問題

個人的理解：

• 抽象數據類型類似于“概念”一說，并不涉及具體、個別，而是使用抽象的概括進行說明，可以認為即為大綱，不過分細分內容，不涉及如何具體實現，該抽象數據類型可以適用于個別具體的對象（對象集和操作集）。
• 數據結構的含義，大體為數據對象中數據的聯系及對數據的操作、函數。
• 該節課講的內容為：數據組織方式、空間利用率、算法的重要性。