[BJOI2018] 染色
神仙結論題，證明思路是 Alex_Wei 的。

我們設 \(S_u=(A,B)\) 表示 \(u\) 的顏色集合是 \(\{ A,B \}\)，\(a_u\) 表示 \(u\) 的顏色。
首先有一些比較顯然的事情：

1. 不是二分圖就一定無解，所以只有偶環。
2. 度數為 \(1\) 的點不影響答案，可以刪去，所以可以不斷去掉度數為 \(1\) 的點，下面假設圖上只存在度數 \(\ge 2\) 的點。
3. 每個連通塊可以分別考慮，下面假設圖連通。

性質

有兩個比較重要的性質。

性質一

考慮如下一條 \(S\) 相同的鏈，那么當第一個點的顏色確定了鏈上每個點的顏色也確定了，且以 \(2\) 為周期交替出現。

性質二

對于一個四元環，我們可以使得環上某個點只能取一種固定的顏色。

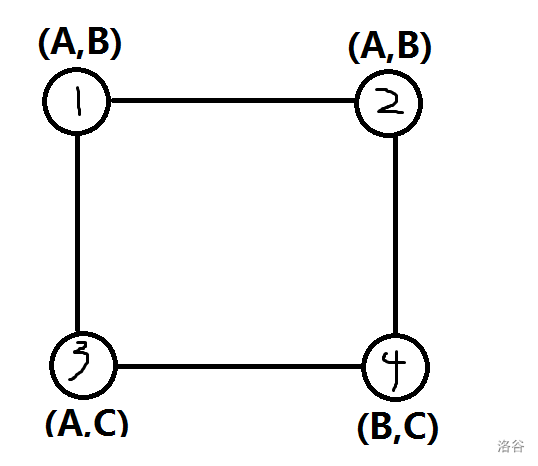
比如上圖我們就固定了 \(a_1\) 只能取 \(B\)。
進一步的，不難發現對于任何環我們都可以通過類似的構造使得環上某個點只能取一種固定的顏色。

一些無解情況

通過上面兩條性質我們可以推出一些無解情況。

兩個由路徑連接起來的簡單環

對兩個簡單環，如果他們之間由一條路徑連接起來，假設這條路徑的兩個端點為 \(u,v\)，其中 \(u,v\) 分別在兩個環上，那么我們可以讓這條路徑上的點 \(S\) 都相同（假設為 \((A,B)\)），然后根據性質二通過第一個環固定 \(a_u=A\)，進一步的根據性質一得出 \(v\) 的顏色，然后再通過第二個環把 \(a_v\) 固定成另一個顏色推出矛盾。所以這種情況無解。
特殊地，當兩個環相交于一點的時候，路徑退化成一個點，此時一樣無解。

兩條相交路徑

假設從 \(u\) 到 \(v\) 有兩條在除了端點處相交的路徑 \(P_1,P_2\)，設他們相交的點為 \(x_1,x_2,...,x_k\)（\(x_i\ne u,v\)），則 \(u-^{P_1}\to x_1-^{P_2}\to u\) 和 \(v-^{P_1}\to x_k-^{P_2}\to v\) 這兩個環通過一條 \(x_1 \to x_k\) 的路徑連接，無解。

四度點

這里的四度點指度數 \(\ge 4\) 的點

兩個四度點

我們將舉出反例證明此時無解。
這兩個四度點之間必定有四條路徑 \(P_1,P_2,P_3,P_4\)，且根據上面的分析這四條路徑互不相交。由于是二分圖，所以 \(P_1,P_2,P_3,P_4\) 長度的奇偶性相同。根據性質一如果某一條路徑的長度 \(>3\) 那么我們可以把它的長度 \(-2\)，不影響反例的正確性，所以下面認為他們的長度 \(\le 3\)。

• 如果他們的長度為奇數，那么因為沒有重邊，必定存在三條路徑的長為 \(3\)，反例如下：
  

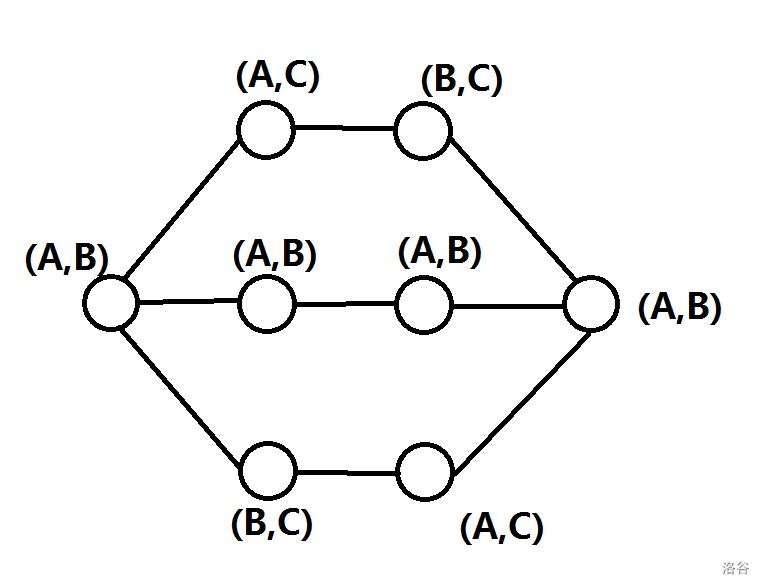
• 如果長度為偶數，那么長度均為 \(2\)，反例如下：
  

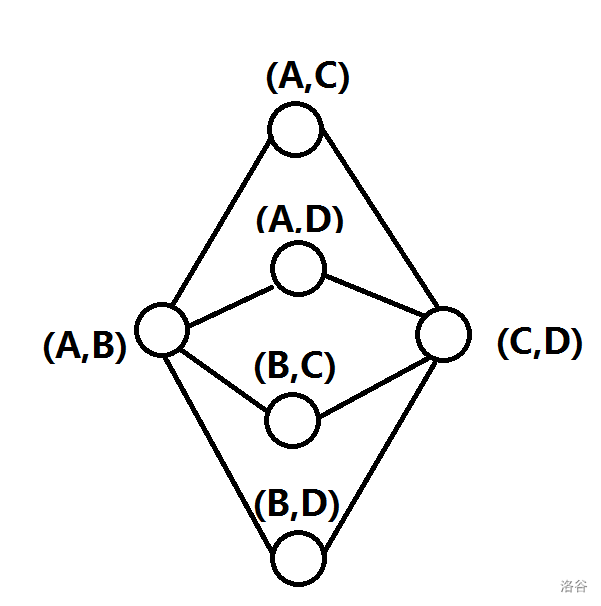
可以發現這兩個其實本質上還是兩個環的無解情況。

一個四度點

如果不存在三度點，那么剩下的只有二度點，圖形如兩個環交于一點，無解；如果存在三度點，那么因為度數之和為偶數，所以至少存在兩個三度點，而這兩個三度點之間的路徑必定交于這個四度點，無解。

綜上如果圖存在四度點就無解。

三度點

若存在三度點，那么至少存在兩個，而類似于上面"一個四度點"的后半部分的分析，只能存在兩個三度點。
仍然考察他們之間的三條不交路徑 \(P_1,P_2,P_3\)，假設 \(|P_1|\ge |P_2| \ge |P_3|\)。

如果長度為奇數，那么當 \(|P_1|=|P_2|=3,|P_3|=1\) 時，反例只需要把"兩個四度點的奇數情況"的反例中間那兩個點去掉即可。對于其他情況根據性質一都可以歸約到這個情況。、
所以長度只能是偶數，而根據 \(|P_1|=|P_2|=3,|P_3|=1\) 的反例不難構造出 \(|P_1|=|P_2|=4,|P_3|=2\) 的反例，所以有 \(|P_1|\ge 2,|P_2|=|P_3|=2\)，即圖長這個樣子：

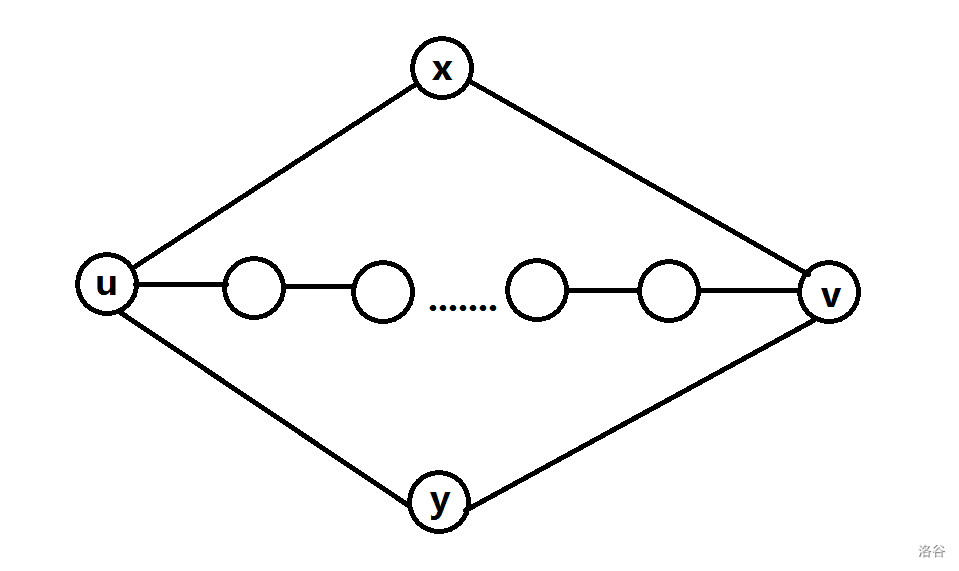
若 \(P_1\) 上的點的 \(S\) 都相同，那么因為 \(|P_1|\) 是偶數，所以 \(a_u=a_v\)，\(a_x,a_y\) 顯然有解。
否則，假設 \(S_u=(A,B)\)，那么當 \(a_u=A\) 時 \(a_v\) 兩種顏色都可以取，當 \(a_u=B\) 時 \(a_v\) 至少有一種取值可以取（或者反過來），也就是說 \(a_u,a_v\) 的組合至少有三種是合法的（一共四種）：

• \(| S_u \cap S_v | \le 1\)：此時三種組合互不相同，根據鴿巢原理，三種組合中至少有一種能使得 \(a_x,a_y\) 都有解。
• \(S_u=S_v\)：此時有兩種組合滿足 \(a_u=a_v\)，那么必定有一組是合法的，有解。

綜上有解當且僅當 \(|P_1|\ge 2,|P_2|=|P_3|=2\)。

結論

最后的結論就是，輸出 YES 當且僅當：

1. 只存在二度點，即圖是若干個不相交的簡單環。
2. 只存在度數 \(\le 3\) 的點，且恰好有兩個三度點，且有至少兩個二度點同時和這兩個三度點相鄰。