[COI 2025] 象掌獸 / Lirili Larila 題解
題目傳送門:[COI 2025] 象掌獸 / Lirili Larila。
我宣布 夏蟲 和 [Ynoi2007] rgxsxrs 的代碼難度在這題面前都弱爆了。
下面的題解幾乎完全復(fù)制了模擬賽的出題人的題解,稍微修改了一些小錯誤并加上了一些細節(jié)。但是因為我不知道出題人是誰,所以無法 @ 出他,對此我深感抱歉。如果這位出題人看到了這篇博客麻煩告知一下,我方便指出出處。順便讓我知道一下是哪位毒瘤把這個東西放 T2。
算法一
我會暴力!
枚舉 \(s,t\) 然后 \(O(n + m)\) BFS 跑最短路并判斷。
時間復(fù)雜度 \(O(n^2(n + m))\),期望得分 \(6\)。
算法二
我會樹!
以下稱 \(dis(s, u) < dis(t, u)\) 的點為 \(A\) 類點,\(dis(s, u) > dis(t, u)\) 的點為 \(B\) 類點,\(dis(s, u) = dis(t, u)\) 的點為 \(C\) 類點。
若 \(dis(s, t) \ge 3\),那么讓 \(s\) 和 \(t\) 分別朝向?qū)Ψ揭苿右徊剑悬c的類別不變。所以只用考慮 \(dis(s, t) \le 2\) 的情況。
若 \(dis(s, t) = 1\),枚舉這條邊,那么 \(A\) 類點在 \(s\) 子樹內(nèi),\(B\) 類點在 \(t\) 子樹內(nèi)。
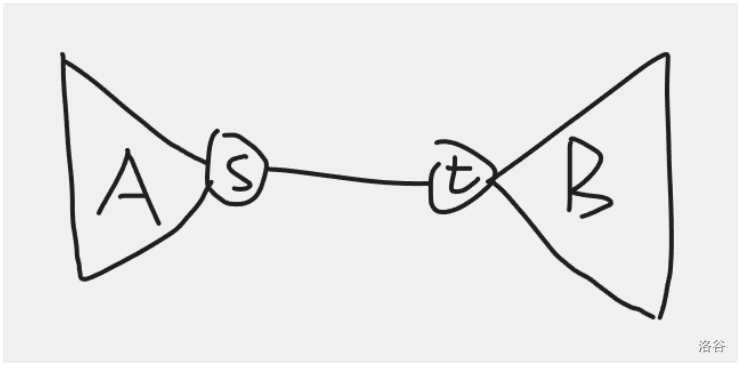
若 \(dis(s, t) = 2\),枚舉路徑中點 \(x\),那么以 \(x\) 為根,\(x\) 的所有子樹中,恰好有一棵子樹,其中所有點都是 \(A\) 類點,恰好有一棵子樹,其中所有點都是 \(B\) 類點。其他點都是 \(C\)類點。
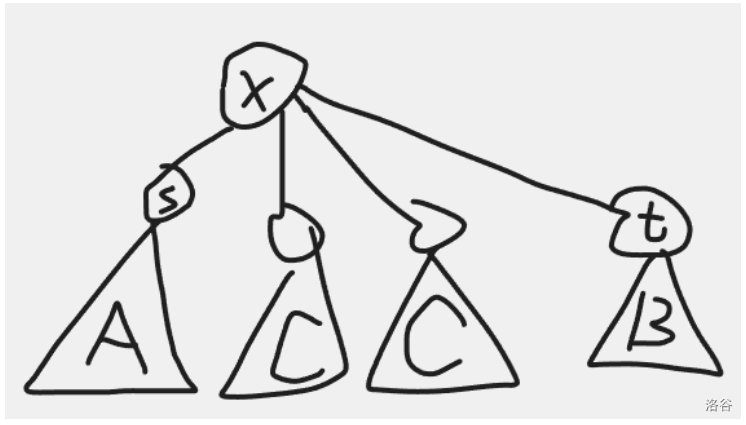
時間復(fù)雜度 \(O(n)\),結(jié)合算法一期望得分 \(39\)。
算法三
我會基環(huán)樹且 \(s,t\) 都在環(huán)上!
設(shè)環(huán)長為 \(l\)。若 \(l\) 是奇數(shù),那么環(huán)上有長度為 \(\frac{l?1}{2}\) 的一段子樹都是 \(A\) 類點,有長度為 \(\frac{l?1}{2}\) 的一段子樹都是 \(B\) 類點,恰好有一棵子樹是 \(C\) 類點。
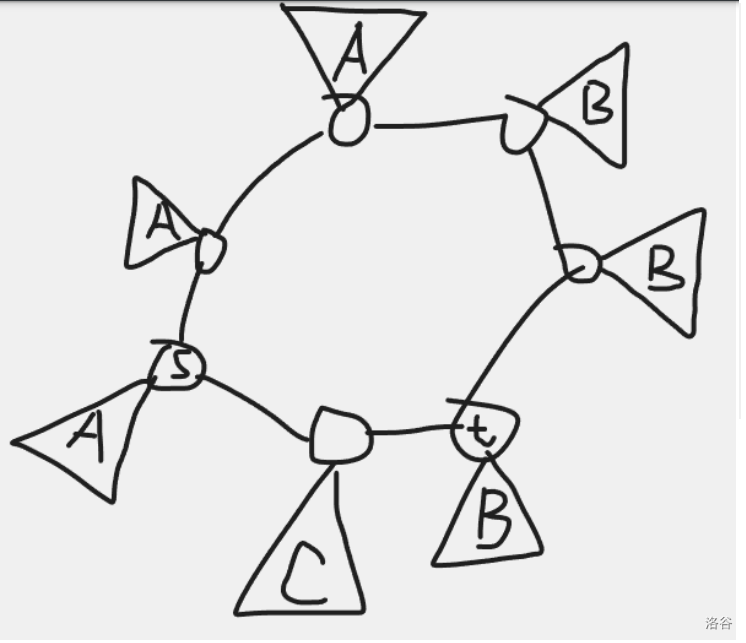
若 \(l\) 是偶數(shù),有兩種情況。
第一種情況是環(huán)上有長度為 \(\frac{l}{2}\) 的一段子樹都是 \(A\) 類點,有長度為 \(\frac{l}{2}\) 的一段子樹都是 \(B\) 類點,沒有 \(C\) 類點。
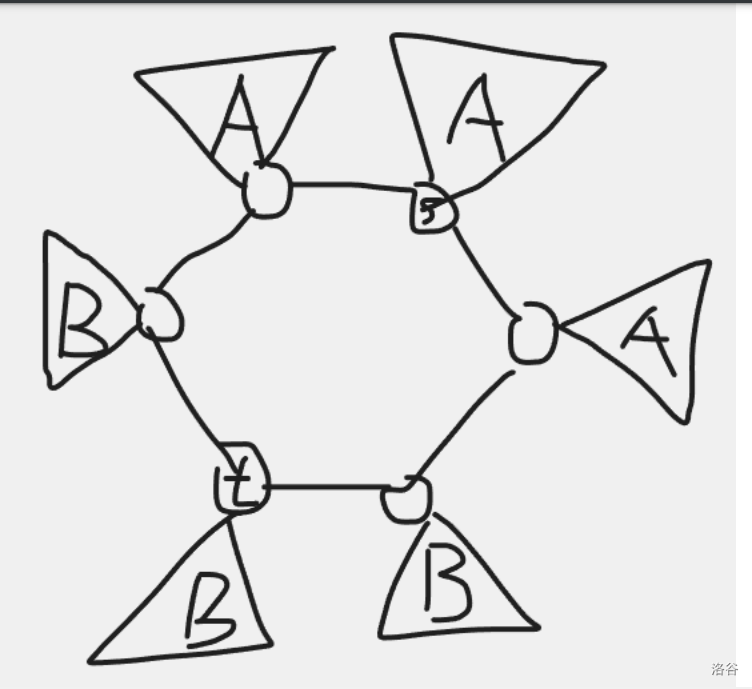
第二種情況是環(huán)上有長度為 \(\frac{l}{2}?1\) 的一段子樹都是 \(A\) 類點,有長度為 \(\frac{l}{2}?1\) 的一段子樹都是 \(B\) 類點,兩個區(qū)間之間有兩棵子樹是 \(C\) 類點。
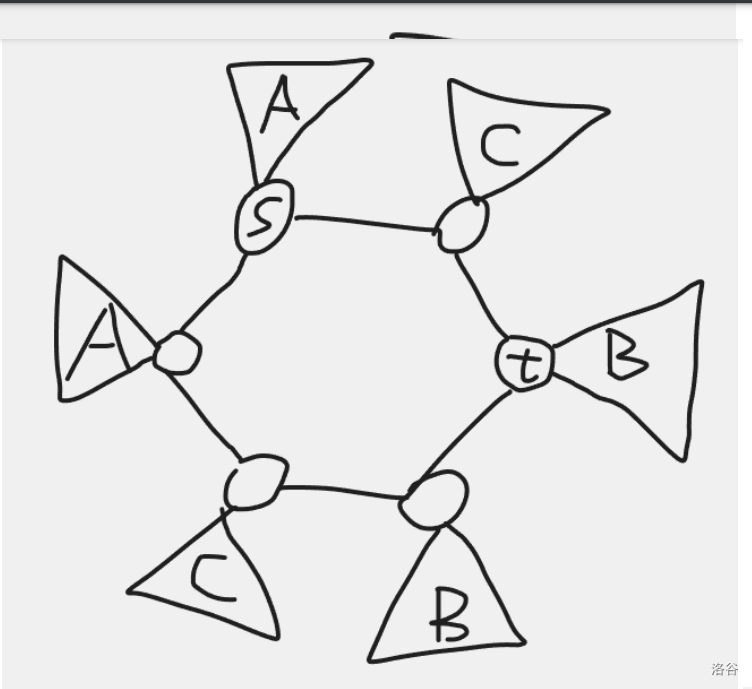
枚舉選的 \(A\) 類點子樹區(qū)間然后討論 \(C\) 類點子樹的位置即可確定 \(B\) 類點子樹區(qū)間。
時間復(fù)雜度 \(O(n)\),結(jié)合算法一和算法二期望得分 \(56\)。
算法四
我會基環(huán)樹!
若 \(s,t\) 的路徑不經(jīng)過環(huán),用樹的做法即可。
若 \(s,t\) 的路徑經(jīng)過環(huán),且 \(s\) 和 \(t\) 都不在環(huán)上,那么讓 \(s\) 和 \(t\) 分別朝向?qū)Ψ揭苿右徊剑悬c的類別不變。所以只用考慮 \(s\) 和 \(t\) 至少有一個在環(huán)上的情況。
若在環(huán)上的點為 \(t\),設(shè) \(s\) 在環(huán)上點 \(x\) 的子樹內(nèi),那么需要滿足 \(s\) 到 \(x\) 的最短路小于等于 \(t\) 到 \(x\) 的最短路,否則同樣可以通過移動歸約為 \(s,t\) 的路徑不經(jīng)過環(huán)的情況。反之亦然。
發(fā)現(xiàn)此時點的類別的情況和 \(s,t\) 都在環(huán)上的大致相同。設(shè)環(huán)長為 \(l\)。
若 \(l\) 是奇數(shù),那么環(huán)上有長度為 \(k (1 \le k \le l ? 2)\) 的一段子樹都是 \(A\) 類點,有長度為 \(l ? 1 ? k\) 的一段子樹都是 \(B\) 類點,恰好有一棵子樹是 \(C\) 類點。
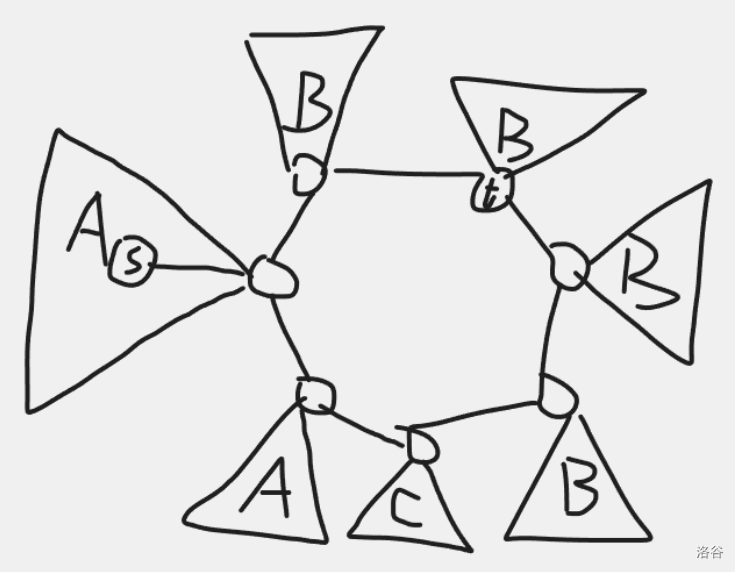
若 \(k \le l ? 1 ? k\)(如上圖),那么 \(t\) 在環(huán)上。我們需要在 \(A\) 類子樹找一個到環(huán)的距離 \(=\frac{l?1?2k}{2}\) 的點(可以用 ST 表查詢區(qū)間最大值位置求出在哪棵子樹內(nèi))。然后根據(jù) \(s\) 在哪棵子樹內(nèi)就可以確定 \(t\) 的位置。
\(k > l ? 1 ? k\) 的情況無非就是變成 \(s\) 在環(huán)上,交換一下 \(A,B\) 再做一遍即可。
若 \(l\) 是偶數(shù),有兩種情況。
第一種情況是環(huán)上有長度為 \(k (1 \le k \le l ? 1)\) 的一段子樹都是 \(A\) 類點,有長度為 \(l ? k\) 的一段子樹都是 \(B\) 類點,沒有 \(C\) 類點。
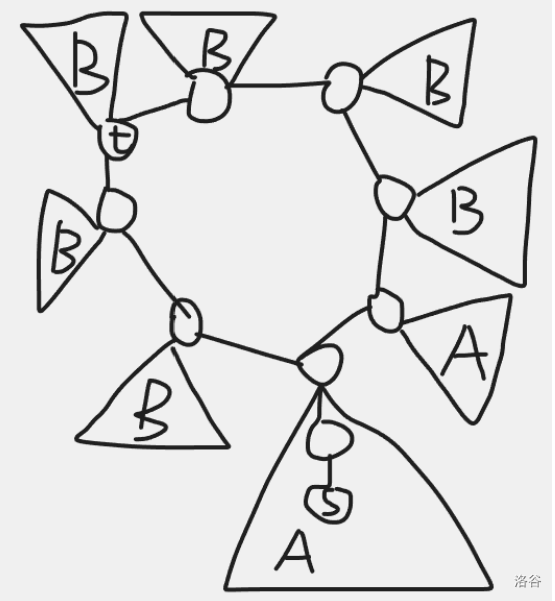
若 \(k \le l ? k\)(如上圖),那么 \(t\) 在環(huán)上。我們需要在 \(A\) 類子樹找一個到環(huán)的距離 \(=\frac{l?2k}{2}\) 的點。\(k > l ? k\) 的情況大致相同。
第二種情況是環(huán)上有長度為 \(k (1 \le k \le l ? 1)\) 的一段子樹都是 \(A\) 類點,有長度為 \(l ? 2 ? k\) 的一段子樹都是 \(B\) 類點,兩個區(qū)間之間有兩棵子樹是 \(C\) 類點。
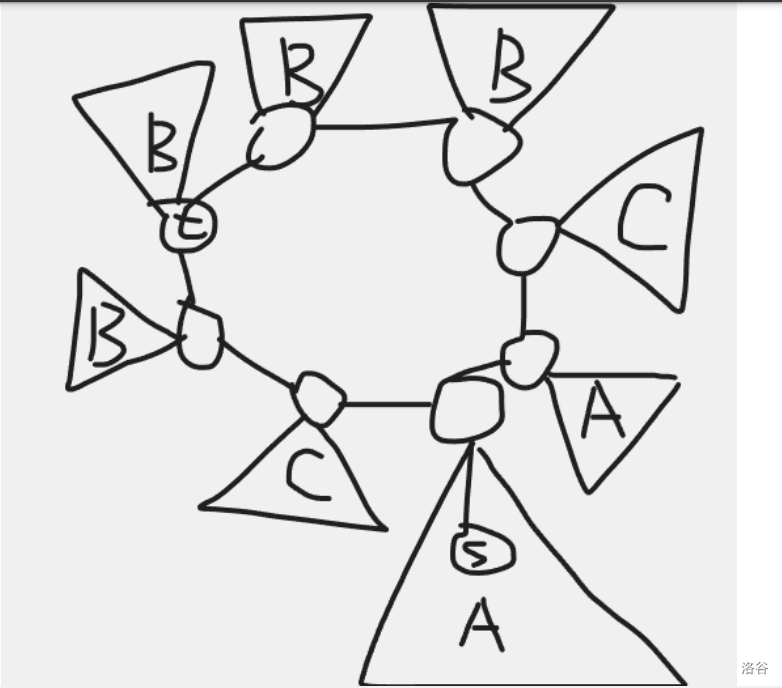
若 \(k \le l ? 2 ? k\)(如上圖),那么 \(t\) 在環(huán)上。我們需要在 \(A\) 類子樹找一個到環(huán)的距離 \(=\frac{l?2?2k}{2}\) 的點。\(k > l ? 2 ? k\) 的情況大致相同。
以上情況都可以枚舉 \(A\) 類子樹區(qū)間的左端點然后雙指針出第一個滿足區(qū)間子樹和 \(\ge A\)(這個 \(A\) 是題面給的 \(A\)) 的右端點,討論 \(C\) 類點子樹的位置即可確定 \(B\) 類點子樹區(qū)間,從而算出 \(t\) 的位置。
不過有一種特殊情況。
不妨設(shè)在環(huán)上的點為 \(t\),設(shè) \(s\) 在環(huán)上點 \(x\) 的子樹內(nèi),則特殊情況為 \(t\) 到 \(x\) 的最短路恰好等于 \(s\) 到 \(x\) 的最短路。此時環(huán)上恰好有一段 \(C\) 類點和一段 \(B\) 類點。特別地,\(x\) 往 \(s\) 方向的子樹是 \(A\) 類點,\(x\) 的其他子樹是 \(C\) 類點。
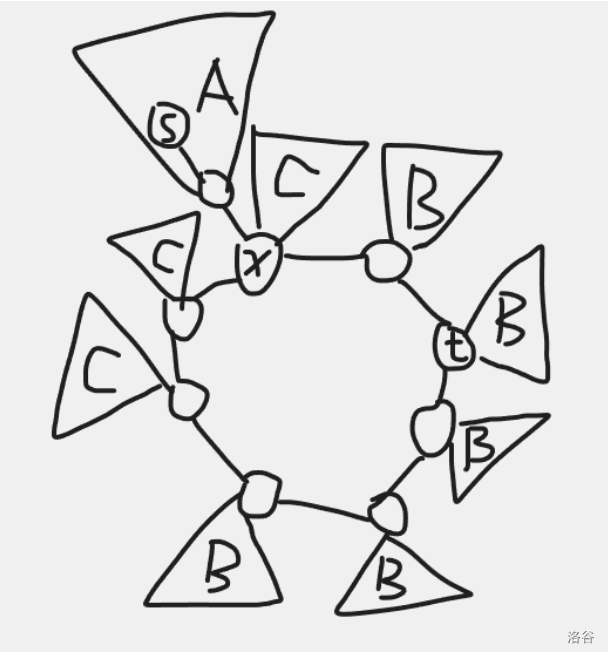
此時我們?nèi)ルp指針 \(B\) 類點子樹區(qū)間,并討論 \(x\) 是在這個區(qū)間的左邊還是右邊,設(shè)這個區(qū)間長度為 \(k\),環(huán)長為 \(l\)。那么 \(s\) 到 \(x\) 的距離需要等于 \(x\) 到 \(t\) 的距離也就是 \(k?\lfloor \frac{l?1}{2} \rfloor+1\)(注意這個時候得 check 一下 \(x\) 是否真的有大小為 \(A\) 的子樹)。
時間復(fù)雜度 \(O(n \log n)\),結(jié)合算法一和算法二期望得分 \(77\)。
算法五
我會正解!
考慮直接把樹和基環(huán)樹的想法結(jié)合起來。
先考慮 \(dis(s, t) = 1\) 且 \(s, t\) 不在同一個環(huán)的情況。再考慮 \(dis(s, t) = 2\) 且若設(shè) \(x\) 為 \(s\) 到 \(t\) 路徑中點則 \(s, x, t\) 都不在同一個環(huán)內(nèi)的情況。
接下來的想法和基環(huán)樹類似。若 \(s,t\) 兩個點都不在環(huán)上,那么讓 \(s\) 和 \(t\) 分別朝向?qū)Ψ揭苿右徊剑悬c的類別不變。
所以枚舉一個環(huán)使得 \(s, t\) 至少有一個在這個環(huán)上。不妨設(shè) \(t\) 在環(huán)上,\(x\) 為 \(s\) 到這個環(huán)的必經(jīng)點,那么需要滿足 \(s\) 到 \(x\) 的最短路小于等于 \(t\) 到 \(x\) 的最短路。
對原圖建出圓方樹后,我們需要求出每個點 \(u\) 子樹內(nèi)(記作 \(d_1\))和子樹外(記作 \(d_2\))所有點到 \(u\) 的最短路的長度最大值。可以通過換根 DP 求出。
換根時,圓點向方點的轉(zhuǎn)移是簡單的,只需要處理一下兒子的 \(d_1\) 的前綴和后綴 \(\max\) 即可快速轉(zhuǎn)移。
在方點向圓點轉(zhuǎn)移時,如果這個方點代表的環(huán)上的點是 \(u_1,u_2,...,u_l\) 要轉(zhuǎn)移的原點是 \(u_i\),相當于是說我們要求 \(\max_{j\ne i} (min(|i ? j|, l ? |i ? j|)+d(a_j))\),其中 \(d(u)\) 表示點 \(u\) 在環(huán)以外的子樹的最大深度(根據(jù)他的位置可能是 \(d_1\) 也可能是 \(d_2\))。用 ST 表維護區(qū)間 \(d(a_j)+j\) 和 \(d(a_j)-j\) 的最大值,轉(zhuǎn)移時根據(jù) \(|i ? j|\) 和 \(l ? |i ? j|\) 的關(guān)系分成兩部分轉(zhuǎn)移即可。
接下來的討論和算法四的部分沒有區(qū)別,故不贅述。
時間復(fù)雜度 \(O(n \log n)\),期望得分 \(100\) 分。
點擊查看代碼
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define eb emplace_back
#define P pair<pair<int,pair<int,int>>,int>
#define PII pair<int,int>
#define fi first
#define se second
#define mk make_pair
#define None mk(mk(0,mk(0,0)),0)
using namespace std;
const int N=2e5+5,M=4e5+5,inf=0x3f3f3f3f;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int T,n,m,A,B,s,t,tot,head[N],to[M<<1],Next[M<<1];
void add(int u,int v){ to[++tot]=v,Next[tot]=head[u],head[u]=tot; }
int c[N],dfn[N],low[N],siz[N<<1],cnt,num,sta[N],top;
int nxt[N],id[N],real_siz[N],real_dep[N]; //每個點在環(huán)上的后繼,編號,往外的子樹的大小以及最大深度
vector<int> G[N<<1];
void tarjan(int u){
dfn[u]=low[u]=++num,sta[++top]=u;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
++cnt;
vector<int> vec;
int x;
do{
siz[cnt]++;
x=sta[top--];
vec.eb(x);
G[x].eb(cnt),G[cnt].eb(x);
}while(x!=v);
siz[cnt]++;
G[u].eb(cnt),G[cnt].eb(u);
if(siz[cnt]>=3){
int lst=u;
c[u]=cnt;
for(int x:vec) c[x]=cnt,nxt[x]=lst,lst=x;
nxt[u]=lst;
}
}
}
else low[u]=min(low[u],dfn[v]);
}
}
int fa[N<<1],Size[N<<1],mxdep[N<<1];
void dfs(int u){
if(fa[u]) G[u].erase(find(G[u].begin(),G[u].end(),fa[u]));
if(u>n&&siz[u]>=3){
id[fa[u]]=0;
for(int x=fa[u];nxt[x]!=fa[u];x=nxt[x]) id[nxt[x]]=id[x]+1;
sort(G[u].begin(),G[u].end(),[&](int x,int y){return id[x]<id[y];});
}
Size[u]=(u<=n)?1:0,mxdep[u]=0;
int v_A=0,v_B=0;
for(int v:G[u]){
fa[v]=u;
dfs(v);
Size[u]+=Size[v];
if(u<=n) mxdep[u]=max(mxdep[u],mxdep[v]);
else if(siz[u]==2) mxdep[u]=mxdep[v]+1;
else mxdep[u]=max(mxdep[u],mxdep[v]+min(id[v],siz[u]-id[v]));
if(u<=n&&siz[v]==2){
if(Size[v]==A&&!v_A) v_A=G[v][0];
if(Size[v]==B) v_B=G[v][0];
if(Size[v]==B&&n-Size[v]==A) s=u,t=G[v][0];
if(Size[v]==A&&n-Size[v]==B) t=u,s=G[v][0];
}
}
if(u>n&&siz[u]>=3){
real_siz[fa[u]]=n-Size[u];
for(int v:G[u]) real_siz[v]=Size[v],real_dep[v]=mxdep[v];
}
if(u<=n&&siz[fa[u]]==2){
if(n-Size[u]==A&&!v_A) v_A=fa[fa[u]];
if(n-Size[u]==B) v_B=fa[fa[u]];
}
if(v_A&&v_B&&v_A!=v_B) s=v_A,t=v_B;
}
int mxdep2[N<<1],pre[N],suf[N];
struct ST{
PII st[20][N<<1];
int len;
void Insert(int x){++len,st[0][len]={x,len};}
void Init(){
for(int t=1;t<=__lg(len);t++){
for(int i=1;i+(1<<t)-1<=len;i++){
st[t][i]=max(st[t-1][i],st[t-1][i+(1<<(t-1))]);
}
}
}
PII RMQ(int l,int r){
if(l>r) return {-inf,0};
int k=__lg(r-l+1);
return max(st[k][l],st[k][r-(1<<k)+1]);
}
}st1,st2;
void dfs2(int u){ //換根 dp 求子樹外的最大深度
if(!G[u].size()) return;
if(u<=n){ //原點向方點貢獻,求出兒子的 mxdep 的前綴 max 和后綴 max 就可以快速轉(zhuǎn)移了
for(int i=0;i<G[u].size();i++){
pre[i]=mxdep[G[u][i]];
if(i) pre[i]=max(pre[i],pre[i-1]);
}
suf[G[u].size()]=0;
for(int i=G[u].size()-1;i>=0;i--) suf[i]=max(mxdep[G[u][i]],suf[i+1]);
for(int i=0;i<G[u].size();i++){
int v=G[u][i];
if(siz[v]==2) mxdep2[v]=max({mxdep2[u],(i==0)?0:pre[i-1],suf[i+1]})+1;
else{
mxdep2[v]=max({mxdep2[u],(i==0)?0:pre[i-1],suf[i+1]});
real_dep[u]=mxdep2[v];
}
}
for(int v:G[u]) dfs2(v); //注意都更新完了再往下遞歸,否則 pre,suf 被改掉了
}
else{
/*
方點向原點貢獻:環(huán)上的點 u 對點 v 的貢獻是 mxdep[u]+min(|id[v]-id[u]|,len-|id[v]-id[u]|),
所以用 ST 表維護區(qū)間 mxdep[u]+id 和 mxdep[u]-id 的最大值即可
*/
if(siz[u]>=3){
int len=siz[u];
st1.len=st2.len=0;
for(int v:G[u]) st1.Insert(mxdep[v]+id[v]),st2.Insert(mxdep[v]-id[v]);
st1.Insert(mxdep2[u]+len),st2.Insert(mxdep2[u]-len);
for(int v:G[u]) st1.Insert(mxdep[v]+id[v]+len),st2.Insert(mxdep[v]-(id[v]+len)); //復(fù)制兩遍
st1.Insert(mxdep2[u]+2*len),st2.Insert(mxdep2[u]-2*len);
st1.Init(),st2.Init();
for(int v:G[u]){
int l=id[v]+1,r=id[v]+len-1,mid=(len+2*id[v])/2;
mxdep2[v]=max(st1.RMQ(l,mid).fi-id[v],st2.RMQ(mid+1,r).fi+len+id[v]);
}
for(int v:G[u]) dfs2(v); //注意都更新完了再往下遞歸,否則 st 表被改掉了
}
else mxdep2[G[u][0]]=mxdep2[u],dfs2(G[u][0]);
}
}
int have_subtree(int u,int S,int d){ //check u 在環(huán)外是否有大小 =S,深度超過 d 的子樹
if(siz[fa[u]]==2&&n-Size[u]==S&&mxdep2[fa[u]]>=d) return fa[fa[u]];
for(int v:G[u]){
if(siz[v]==2&&Size[v]==S&&mxdep[v]>=d) return G[v][0];
}
return 0;
}
namespace Solve{
ST st;
int A,B,a[N<<1],siz[N<<1],dep[N<<1],n,len,S;
void Init(int x,int numA,int numB){
A=numA,B=numB,n=S=0;
int u=x;
do{
a[++n]=u,siz[n]=real_siz[u],dep[n]=real_dep[u],S+=siz[n];
u=nxt[u];
}while(u!=x);
len=n;
for(int i=1;i<=len;i++) a[++n]=a[i],siz[n]=siz[i],dep[n]=dep[i];
st.len=0;
for(int i=1;i<=n;i++) st.Insert(dep[i]);
st.Init();
}
int dist(int x,int y){return min(y-x,x+len-y);}
P solve1(){ //環(huán)長是奇數(shù)
for(int l=1,r=1,sum=0;l<=len;l++){
while(r<=l+len-1&&sum<A) sum+=siz[r],r++; //注意 [l,r) 左閉右開
int k=r-l,d=(len-2*k-1)/2; //k 算出來的是 A 區(qū)間的點的個數(shù)
PII mx=st.RMQ(l,r-1);
int x=mx.se,t=x+2*(r-x)+d;
if(sum!=A||2*k>len-1||mx.fi<d){sum-=siz[l]; continue;}
if(S-sum-siz[r]==B&&d<dist(x,t)){ //C 類點是 r
return {{a[x],{d,-1}},a[t]};
}
t--;
if(S-sum-siz[l+len-1]==B&&d<dist(x,t)){ //C 類點是 l-1
return {{a[x],{d,-1}},a[t]};
}
sum-=siz[l];
}
return None;
}
P solve2(){ //環(huán)長是偶數(shù),沒有 C 類點
for(int l=1,r=1,sum=0;l<=len;l++){
while(r<=l+len-1&&sum<A) sum+=siz[r],r++;
int k=r-l,d=(len-2*k)/2;
PII mx=st.RMQ(l,r-1);
int x=mx.se,t=r+(d+(r-x)-1);
if(sum!=A||2*k>len||mx.fi<d){sum-=siz[l]; continue;}
if(S-sum==B&&d<dist(x,t)){
return {{a[x],{d,-1}},a[t]};
}
sum-=siz[l];
}
return None;
}
P solve3(){ //環(huán)長是偶數(shù),有 C 類點
for(int l=1,r=1,sum=0;l<=len;l++){
while(r<=l+len-1&&sum<A) sum+=siz[r],r++;
int k=r-l,d=(len-2*k-2)/2;
PII mx=st.RMQ(l,r-1);
int x=mx.se,t=r+(d+(r-x));
if(sum!=A||2*k>len-2||mx.fi<d){sum-=siz[l]; continue;}
if(S-sum-siz[r]-siz[l-1+len]==B&&d<dist(x,t)){
return {{a[x],{d,-1}},a[t]};
}
sum-=siz[l];
}
return None;
}
P solve4(){ //特殊情況,此時需要雙指針 B 類區(qū)間
for(int l=1,r=1,sum=0;l<=len;l++){
while(r<=l+len-1&&sum<B) sum+=siz[r],r++;
if(sum!=B){sum-=siz[l]; continue;}
int y=(len-1)/2;
// x 是 l-1
int t=r-1-y,x=l-1+len,d=dist(l,t)+1;
if(t>=l&&d>0&&have_subtree(a[x],A,d)){
return {{a[x],{d,A}},a[t]};
}
// x 是 r
t=l+y,x=r,d=dist(t,x);
if(t<r&&d>0&&have_subtree(a[x],A,d)){
return {{a[x],{d,A}},a[t]};
}
sum-=siz[l];
}
return None;
}
P work(){ //返回值 {{x,{d,size}},y} 表示 s 是 x 大小是 size 的子樹內(nèi)深度為 d 的點,t 是 y
P res=solve4();
if(res!=None) return res;
if(len&1) return solve1();
else{
res=solve2();
if(res==None) res=solve3();
return res;
}
}
};
bool vis[N];
int find(int x,int d,int S){ //BFS 找要求的點
for(int i=1;i<=n;i++) vis[i]=0;
queue<PII> Q;
if(S==-1) Q.push({x,0}),vis[x]=true;
else{
int y=have_subtree(x,S,d);
Q.push({y,1}),vis[y]=true;
}
while(Q.size()){
int u=Q.front().fi,dis=Q.front().se; Q.pop();
if(dis==d) return u;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(vis[v]||c[v]==c[x]) continue;
Q.push({v,dis+1}),vis[v]=true;
}
}
}
void Init(){
tot=num=s=t=0;
for(int i=1;i<=n;i++) c[i]=head[i]=dfn[i]=low[i]=0;
for(int i=1;i<=cnt;i++) G[i].clear(),siz[i]=0,mxdep2[i]=0;
}
void work(){
Init();
n=read(),m=read(),A=read(),B=read();
for(int i=1;i<=m;i++){
int u=read(),v=read();
add(u,v),add(v,u);
}
cnt=n;
for(int i=1;i<=n;i++) if(!dfn[i]) top=0,tarjan(i);
dfs(1); if(s) return;
dfs2(1);
for(int i=n+1;i<=cnt;i++){
if(siz[i]==2) continue;
bool stater=false;
Solve::Init(fa[i],A,B);
P res=Solve::work();
if(res==None){
stater=true;
Solve::Init(fa[i],B,A);
res=Solve::work();
}
if(res==None) continue;
s=find(res.fi.fi,res.fi.se.fi,res.fi.se.se),t=res.se;
if(stater) swap(s,t);
return;
}
}
signed main(){
// freopen("recallrevenge.in","r",stdin);
// freopen("recallrevenge.out","w",stdout);
T=read();
while(T--) work(),printf("%d %d\n",s,t);
return 0;
}


 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號