這題的幾個 trick 還是比較重要的。

題目傳送門：洛谷&QOJ。

下面默認 \(\frac{n}{2}\) 下取整。

這種詢問樹上三個點的關系的題有一個經典策略是拉出一條鏈來考慮。

我們不妨先思考樹是一條鏈的情況。
首先容易用 \(n\) 次詢問找出這條鏈的兩端，具體來講就是先隨便欽定兩個點 \(l,r\)，然后詢問其他點 \(u\)，把 \(l,r\) 替換成 \(l,r,u\) 中不是 \(ask(l,r,u)\) 的那兩個點。
然后考慮隨機二分。
我們在鏈上每次隨機一個點 \(x\)，用 \(len\) 次詢問（\(len\) 是當前鏈長）求出它左邊和右邊的點的個數，如果點數均為 \(\frac{n}{2}\)，那它就是重心，否則遞歸到大的那一邊去做。
因為每一次期望刪掉 \(\frac{1}{4}\) 的點，所以總復雜度期望是 \(O(n+\frac{3}{4}n+\frac{9}{16}n+...)=O(n)\)。（差不多 \(4n\) 次詢問，算上開頭那 \(n\) 次剛剛好可以過鏈的部分分）。

接下來看一般情況。
因為重心的每個子樹大小不超過 \(\frac{n}{2}\)，所以每次隨機兩個點 \(x,y\) 重心在這兩個點的路徑上的概率至少是 \(\frac{1}{2}\)。

證明：假設重心的每棵子樹大小是 \(a_1,a_2,a_3,...,a_k\)，那么重心不在 \(x,y\) 路徑上的概率是 \(\frac{\sum_{i=1}^k a_i^2}{n^2}\)。
因為 \(\forall i\in [1,k]，a_i \le \frac{n}{2}\)，所以 \(k\ge 2\)，而由于 \(x^2+y^2\le (x+y)^2\)，所以要使分子取到最大值 \(k=2\)，即 \(a_1=a_2=\frac{n}{2}\)，此時概率是 \(\frac{1}{2}\)。

所以只需要隨機 \(O(1)\) 次就可以找到一條經過重心的鏈。
我們每次找出隨機的鏈上有可能是重心的點，并 check 它是否真的是重心就可以了。

假設當前的鏈是 \(x,y\)，點集是 \(S\)，初始時 \(S\) 是全集，我們用 \(|S|\) 次詢問就可以求出哪些點在鏈上，哪些點掛在 \(x,y\) 下面，哪些點掛在鏈上其他點的下面。
可能成為重心的點 \(u\) 需要滿足他左邊的點集（不包括自己） \(L\) 和右邊的點集（不包括自己） \(R\) 的大小都 \(\le \frac{n}{2}\)（容易證明一條鏈上這樣的 \(u\) 有且僅有一個），如下圖：

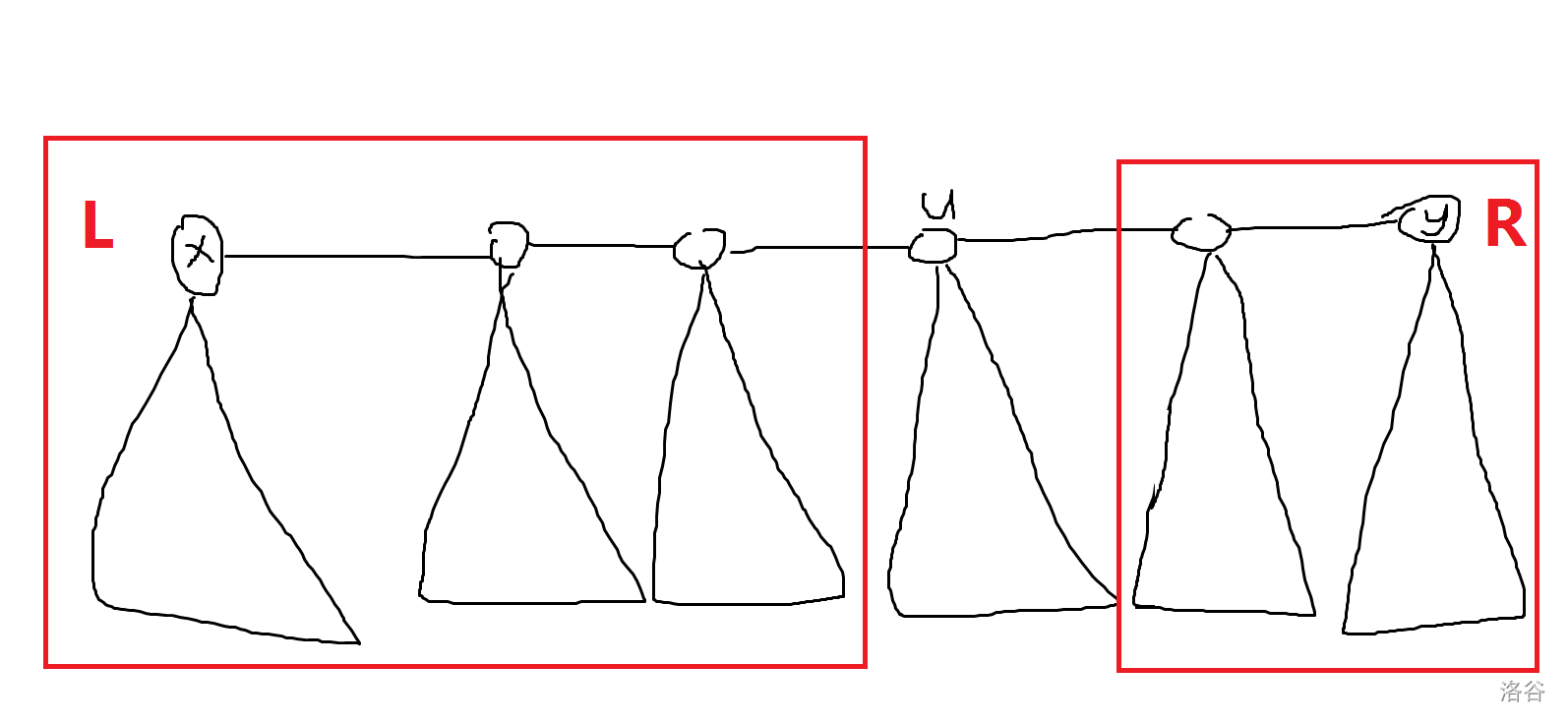
我們先判掉端點 \(x,y\) 是 \(u\) 的情況，下面只需要考慮 \(u\) 是鏈上其他點的情況。
如果我們隨機一個 \(u\)，那么可以用 \(|S|\) 次詢問求出一個點屬于 \(L,R\) 和 \(u\) 子樹中的哪個，具體來講對于一個點 \(v\)：

1. 如果 \(ask(x,u,v)\ne u\)，那 \(v\) 就屬于 \(L\)。
2. 否則如果 \(ask(y,u,v)\ne u\)，那 \(v\) 就屬于 \(R\)。
3. 其他情況 \(v\) 就屬于 \(u\) 子樹。

如果 \(L,R\) 的大小都不超過 \(\frac{n}{2}\)，那 \(u\) 就是要找的點，否則扔掉小的那部分遞歸去做。（\(u\) 子樹會被保留）
注意： 比如說 \(R> \frac{n}{2}\)，那么會扔掉 \(L\)，但是雖然之后 \(L\) 內的點不再屬于 \(S\)，但是他們仍然要考慮到之后的子問題的 \(L\) 中。

但是因為此時樹不再是一條鏈，所以每次隨機二分，并不能期望刪掉 \(\frac{1}{4}\) 的點（比如這條鏈上某一邊有個點的子樹特別大，但是你隨到的點一直在另一邊），復雜度和詢問次數都是錯的。
于是我們考慮帶權二分，原先每個點被隨到的概率都是一樣的，現在我們希望一個子樹大小是 \(siz\) 的點被隨到的概率是 \(\frac{siz}{|S|}\)。
但是現在我們并不知道樹的結構，也就不知道每個點的 \(siz\)，好像沒法帶權二分。
但是如果我們在 \(S\) 中隨機一個點 \(v\)，那么這個點是鏈上 \(u\) 子樹內的點的概率正好就是 \(\frac{siz}{S}\)。
所以我們只需要每次隨機一個點 \(v\) 并找到他所對應的鏈上的點就完成了帶權二分的過程。
要找到 \(v\) 所對應的點 \(u\) 可以先假定 \(u=x\) 然后遍歷鏈上的所有點，當遍歷到一個點 \(i\) 時如果 \(ask(v,u,i)=i\) 就令 \(u=i\)。

最后剩下的問題就是怎么 check 一個點 \(u\) 是不是重心。
如果 \(u\) 不是重心，那么必然有一個子樹的大小 \(>\frac{n}{2}\)，所以我們可以考慮用摩爾投票的方法求出這個最大的子樹。
回顧如何用摩爾投票求序列絕對眾數：設 \(x\) 是絕對眾數，并維護一個變量 \(cnt\)，初始時令 \(x\gets a_1,cnt\gets 1\)，對于序列中的其他數 \(y\)，如果 \(x=y\) 就令 \(cnt\gets cnt+1\)，否則令 \(cnt\gets cnt-1\)，如果此時 \(cnt\) 變成負數就令 \(x\gets y,cnt\gets 1\)，如果序列存在絕對眾數那最終的 \(x\) 就是絕對眾數。
同樣的，我們維護一個 \(x\) 表示最大的子樹中的點，同時維護一個變量 \(cnt\)。初始 \(x\) 任取一個點，\(cnt=1\)，當遍歷到一個點 \(y\) 時，如果 \(ask(x,y,u)\ne u\) 意味著 \(x,y\) 在同一個子樹，令 \(cnt\gets cnt+1\)，否則同理。
最后我們再用 \(n\) 次詢問去求出 \(x\) 所在子樹的真實大小看一下是否 \(>\frac{n}{2}\) 即可。

詢問次數是線性的，常數系數不知道。

code
下面這份代碼是以洛谷的交互庫為標準的。

#include<bits/stdc++.h>
#define PII pair<int,int>
#define PIII pair<int,pair<int,int> > 
#define fi first
#define se second 
#define eb emplace_back
#define Debug puts("----------------")
using namespace std;
extern "C"  int ask(int x,int y,int z);
int query(int x,int y,int z){
	if(x==y) return x;
	if(x==z) return x;
	if(y==z) return y;
	return ask(x,y,z);
}
mt19937 rnd(20100307);
int n;
bool flag[50005],in_subx[50005],in_suby[50005];
int solve(int x,int y,int sizL,int sizR,vector<int> node){
	vector<int> list,other;  
	int siz_x=0,siz_y=0;
	if(n==49999){
		siz_x=siz_y=1;
		for(int i:node){
			flag[i]=true;
			if(i==x) in_subx[i]=true; else in_subx[i]=false;
			if(i==y) in_suby[i]=true; else in_suby[i]=false;
			if(i!=x&&i!=y) other.eb(i);		
		}	
	}
	else{
		for(int i:node){
			int u=query(x,y,i);
			if(u==x) siz_x++,in_subx[i]=true; else in_subx[i]=false;
			if(u==y) siz_y++,in_suby[i]=true; else in_suby[i]=false;
			if(u==i) list.eb(i),flag[i]=true;
			else flag[i]=false;
			if(!in_subx[i]&&!in_suby[i]) other.eb(i);
		} 
	}
	
	if(node.size()-siz_x+sizR<=n/2) return x;   //排除 x,y 是重心的情況 
	if(node.size()-siz_y+sizL<=n/2) return y;
	
	int v=other[rnd()%(other.size())],u;
	if(flag[v]) u=v;
	else{
		u=x;
		for(int i:list){
			if(i==x) continue;
			if(query(u,i,v)==i) u=i;	
		}
	}
	
	vector<int> L,R,subtree;
	for(int i:node){
		if(in_subx[i]){
			L.eb(i);
			continue;
		}
		if(in_suby[i]){
			R.eb(i);
			continue;
		}
		if(n==49999){
			if(i==u) subtree.eb(i);
			else{
				int z=query(x,u,i);
				if(z==u) R.eb(i);
				else L.eb(i); 
			}
			continue;
		}
		int z=query(x,u,i);
		if(z==u){
			if(query(u,y,i)==u) subtree.eb(i);
			else R.eb(i);
		}
		else L.eb(i);
	}
	if(L.size()+sizL>n/2){
		for(int i:subtree) L.eb(i);
		return solve(x,u,sizL,sizR+R.size(),L);
	}
	else if(R.size()+sizR>n/2){
		for(int i:subtree) R.eb(i);
		return solve(u,y,sizL+L.size(),sizR,R);		
	}
	return u;
}
bool check(int u){
	int cnt=1,x=1,siz=0;
	if(x==u) x++;
	for(int y=x+1;y<=n;y++){
		if(y==u) continue;
		if(query(x,y,u)!=u) cnt++;
		else{
			cnt--;
			if(cnt<0) x=y,cnt=1;
		}
	}
	for(int y=1;y<=n;y++){
		if(y==u) continue;
		if(query(x,y,u)!=u) siz++;
	}
	return siz<=n/2;
}
extern "C"  int centroid(int id,int N,int M){
	if(N==3) return ask(1,2,3);
	map<PII,bool> mp;
	n=N;
	vector<int> all(n);
	for(int i=1;i<=n;i++) all[i-1]=i;
	if(n==49999){  //注意鏈的情況的特殊數據范圍 
		int l=1,r=2;
		for(int i=3;i<=n;i++){
			int u=query(l,r,i);
			if(u==l) l=i;
			else if(u==r) r=i;
		}	
		return solve(l,r,0,0,all);
	} 
	while(true){
		int x=rnd()%n+1,y=rnd()%n+1;
		while(mp[{x,y}]||x==y) x=rnd()%n+1,y=rnd()%n+1;
		mp[{x,y}]=true;
		int u=solve(x,y,0,0,all);
		if(check(u)) return u;
	}
}

弱弱地問一句，有沒有人會嚴格證明這個帶權二分的期望復雜度，寫的時候突然發現自己不是很會證。