NOI2025 廣東省隊集訓題解
寫在前面
- 只記錄模擬賽 Div1 的題。專題授課的題實在是太多了。
- 能找到原題的都標了。
- 如你所見,作者實力有限,所以很多 T3 都沒有寫(所以神犇們可以不用看了)。以后可能會考慮補。
- 有問題的可以寫在評論區或者私信。
Day1 模擬賽
A.最小生成樹
原題:Spanning Tree Game。
Tip:注意原題與這題的數據范圍的差別。
題意
給一張 \(n\) 個點,\(m\) 條邊的無向圖,每條邊有兩個可能的權值 \(a_i,b_i\),你需要對所有 \(k\in [0,m]\) 求出,當恰好有 \(k\) 條邊的權值是 \(a_i\),\(m-k\) 條邊的權值是 \(b_i\) 時,該圖的最小生成樹的邊權和的最大值是多少。
數據范圍:\(n\le 9,n-1\le m\le 100,a_i,b_i\le 10^8\),保證圖連通且無自環,不保證沒有重邊。
題解
考慮 Kruskal 的流程。
將每條邊拆成兩條邊 \((x,y,a)\) 和 \((x,y,b)\),我們稱他們互為對應邊。
然后把這 \(2m\) 條邊按照邊權升序排序。
依次考慮每條邊 \((x,y,w)\)。
- 他的對應邊還沒有出現過,那么這條邊選不選都可以(不選的話就代表這條邊選了另一個邊權),選的話如果此時 \(x,y\) 不連通就把 MST 的邊權和加上 \(w\)。
- 他的對應邊出現過了,那么如果 \(x,y\) 不連通這條邊就一定要選,并把 MST 的邊權和加上 \(w\),否則這條邊選不選都不影響 MST。
所以設 \(f_{i,j,S}\) 表示考慮了前 \(i\) 條邊,圖的連通性的狀態是 \(S\),有 \(j\) 條邊邊權選了 \(a\)。
轉移的決策就是在第一種情況中選還是不選(注意第二種情況是不會對 \(j\) 這一維產生影響的,因為貢獻在第一種情況里已經算過了),所以為了維護 \(j\) 這一維還需要記錄每條邊的 \(w\) 原來是 \(a\) 還是 \(b\)。
我們可以哈希并查集數組來記錄這個 \(S\)。
合法 \(S\) 的數量為 \(Bell(n)\le 21147\),所以復雜度是 \(O(m^2Bell(n))\),但是遠遠跑不滿。
code
#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
#define LL long long
#define ULL unsigned long long
using namespace std;
const int N=15,M=105,p=13331;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,ans[M];
struct Edge{
int id,x,y,w,op;
}E[M<<1];
bool flag[M<<1];
ULL End;
unordered_map<ULL,int> f[M<<1][M];
unordered_map<ULL,vector<int> > mp;
ULL HASH(vector<int> v){
ULL Hash=0;
for(int x:v) Hash=Hash*p+x;
mp[Hash]=v;
return Hash;
}
void Init(){
sort(E+1,E+2*m+1,[&](Edge e1,Edge e2){return e1.w<e2.w;});
for(int i=1;i<=2*m;i++){
for(int j=1;j<i;j++) if(E[j].id==E[i].id) flag[i]=true;
}
vector<int> v(n+1),v2(n+1);
for(int i=1;i<=n;i++) v[i]=i,v2[i]=1;
End=HASH(v2);
f[0][0][HASH(v)]=0;
}
void chkmax(int &x,int y){x=max(x,y);}
vector<int> merge(vector<int> fa,int x,int y){
int u=fa[x],v=fa[y];
if(u>v) swap(u,v);
for(int i=1;i<=n;i++) if(fa[i]==v) fa[i]=u;
return fa;
}
void dfs(int i){
if(i==2*m){
for(int j=0;j<=m;j++) ans[j]=f[i][j][End];
return;
}
int x=E[i+1].x,y=E[i+1].y,w=E[i+1].w,op=E[i+1].op;
for(int j=0;j<=min(i,m);j++){
for(pair<ULL,int> u:f[i][j]){
vector<int> fa=mp[u.fi];
int res=u.se;
if(flag[i+1]){
if(fa[x]!=fa[y]) chkmax(f[i+1][j][HASH(merge(fa,x,y))],res+w);
else chkmax(f[i+1][j][u.fi],res);
}
else{
chkmax(f[i+1][j+1-op][u.fi],res);
if(fa[x]!=fa[y]) chkmax(f[i+1][j+op][HASH(merge(fa,x,y))],res+w);
else chkmax(f[i+1][j+op][u.fi],res);
}
}
}
dfs(i+1);
}
signed main(){
freopen("mst.in","r",stdin);
freopen("mst.out","w",stdout);
n=read(),m=read();
for(int i=1;i<=m;i++){
int x=read(),y=read(),a=read(),b=read();
E[i]={i,x,y,a,1},E[i+m]={i,x,y,b,0};
}
Init();
dfs(0);
for(int i=0;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
B.操作
原題:Assign or Multiply
Tip:為了卡掉 bitset 本題在原題的基礎上加強了數據,并減少了時限。
題意
給定一個質數 \(p\) 和 \(n\) 個操作,操作有兩種類型:
0 x:表示將 \(w\) 修改為 \(x\)。1 x:表示將 \(w\) 修改為 \((w\times x) \bmod p\)。
其中 \(w\) 是一個初始為 \(1\) 的變量。
現在你可以任意重排這些操作,問 \([0,p-1]\) 中有多少個數無論怎么重排操作都無法得到。
多測,有 \(T\) 組數據。
數據范圍:\(1\le T\le 2,1\le n \le 10^6,2\le p \le 10^6,0\le x < p\),保證 \(p\) 是質數。
亂搞
來自模擬賽一位大佬的做法,直接貼上他的原題解。

實際上因為這個題加強了,所以亂搞比正解還快。
正解
不難發現題意就是問隨便選一個覆蓋操作和若干乘法操作可以得到多少數。特殊的,沒有覆蓋操作答案是 \(p-1\)。
首先取模的乘法沒有啥性質,但是注意到 \(p\) 是個質數,所以可以求出 \(p\) 的原根 \(g\),把每個數表示成 \(g^x\) 的形式(\(0\) 特判),所以就把乘法轉換成加法了。然后你就把覆蓋操作中的數當作背包的初值,接著對第二種操作做01背包即可,可以用 bitset 優化到 \(O(\frac{np}{w})\),顯然出題人不想讓你過去。
下面記 \(M=p-1\)。
觀察這個背包的轉移,不難發現如果現在加入的數是 \(v\) 就是要把所有滿足 \(f_i=true,f_{(i+v) \bmod M} =false\) 的 \(f_{(i+v) \bmod M}\) 設為 \(true\)。
所以實際上有效的修改只有 \(O(p)\) 次,我們如果能快速找到需要修改的位置就可以保證復雜度。
但是 \(f_i=true,f_{(i+v) \bmod M} =false\) 這個限制不太好判斷,不妨弱化一下,找到所有滿足 \(f_i \ne f_{(i+v)\bmod M}\) 的位置,這個可以段環成鏈之后用樹狀數組維護 \(f\) 數組的哈希值然后用二分 \(O(\log^2 p)\) 求出一個符合條件的位置。
可是這樣的復雜度好像不太對,因為你會找到 \(f_i=false,f_{(i+v) \bmod M} =true\) 這樣沒用的位置。
但是這題的背包體積這一維是在取模意義下的,換句話說,如果你按照 \(i \to (i+v)\bmod M\) 連邊,你連出的顯然是若干個環,這就意味此時 \(1\to 0\) 的邊的數量和 \(0\to 1\) 的邊的數量是相等的,所以你找出來了多少 \(1\to 0\) 的邊就也找出了多少條 \(0\to 1\) 的邊,而 \(1\to 0\) 的邊總共只能出現 \(O(p)\) 個,所以復雜度是對的。
放在原題 \(O(n\log^2 p)\) 是穩過的,但這題你可能會被卡常反正我被卡了,這里提供兩個可行的卡常方案:
- 采用二進制分組把相同的物品縮成 \(O(\log n)\) 個。
- 當加入一個物品時,先判斷一下是否有合法的位置,如果沒有就直接跳過這個物品,沒有必要二分。
code
#include<bits/stdc++.h>
#include<cctype>
#define ULL unsigned long long
using namespace std;
const int N=1e6+5,Base=100591,MB=1<<20;
struct FastIO{
char ib[MB+100],*p,*q;
char ob[MB+100],*r,stk[128];
int tp;
FastIO(){p=q=ib,r=ob,tp=0;}
~FastIO(){fwrite(ob,1,r-ob,stdout);}
char read_char() {
if(p==q){
p=ib,q=ib+fread(ib,1,MB,stdin);
if(p==q)return 0;
}
return *p++;
}
template<typename T>
void read_int(T& x) {
char c=read_char(),l=0;
for(x=0;!isdigit(c);c=read_char())l=c;
for(;isdigit(c);c=read_char())x=x*10-'0'+c;
if(l=='-')x=-x;
}
}IO;
int pri[N],cnt,mn[N],mx[N],phi[N];
bool stater[N],flag[N];
int qp(int a,int b,int p){
int ans=1;
while(b){
if(b&1) ans=1ll*ans*a%p;
b>>=1,a=1ll*a*a%p;
}
return ans;
}
void Eular(){
stater[1]=flag[1]=flag[2]=flag[4]=true;
phi[1]=1;
for(int i=2;i<N;i++){
if(!stater[i]){
pri[++cnt]=i;
phi[i]=i-1;
mn[i]=mx[i]=i;
if(i>2){
int x=i;
while(x<N){
flag[x]=true;
if(2*x<N) flag[2*x]=true;
if(x>(N/x)) break;
x*=x;
}
}
}
for(int j=1;pri[j]*i<N&&j<=cnt;j++){
int x=i*pri[j];
stater[x]=true;
mn[x]=pri[j];
if(i%pri[j]==0){
mx[x]=mx[i]*pri[j];
if(x!=mx[x]) phi[x]=phi[x/mx[x]]*phi[mx[x]];
else phi[x]=x/mn[x] * (mn[x]-1);
break;
}
else mx[x]=pri[j],phi[x]=phi[x/mn[x]]*phi[mn[x]];
}
}
}
int p[N],num;
void fenjie(int n){
num=0;
while(n>1) p[++num]=mn[n],n/=mx[n];
}
bool check(int g,int n){
if(__gcd(g,n)!=1) return false;
for(int i=1;i<=num;i++) if(qp(g,phi[n]/p[i],n)==1) return false;
return true;
}
int find(int n){
for(int i=1;i<n;i++) if(check(i,n)) return i;
}
int T,m,n,g,id[N],a[N],n1,b[N],n2,c[N],n3,mod;
bool zero,f[N];
ULL mi[N<<1];
int add(int x,int y){return (x+y)>=mod?(x+y-mod):x+y;}
struct BIT{
ULL c[N<<1];
void Init(){memset(c,0,sizeof c);}
void add(int i,ULL x){for(;i<=2*mod;i+=(i&-i)) c[i]+=x;}
ULL ask(int i){
ULL sum=0;
for(;i;i-=(i&-i)) sum+=c[i];
return sum;
}
void modify(int x){
x++;
add(x,mi[x-1]),add(x+mod,mi[x+mod-1]);
}
ULL query(int l,int r){
l++,r++;
return ask(r)-ask(l-1);
}
}Bit;
void Init(){
fenjie(phi[m]);
int g=find(m);
int x=1;
id[0]=m;
for(int i=1;i<=m-1;i++){
x=1ll*x*g%m;
id[x]=i%(m-1);
}
mod=m-1;
for(int i=1;i<=n1;i++) a[i]=id[a[i]];
for(int i=1;i<=n2;i++) b[i]=id[b[i]];
sort(a+1,a+n1+1);
n1=unique(a+1,a+n1+1)-a-1;
sort(b+1,b+n2+1);
for(int i=1;i<=n2;i++){
if(b[i]==m) break;
int j=i,len=0;
while(j<=n2&&b[j]==b[i]) j++,len++;
j--;
for(int k=1;k<=len;k<<=1) c[++n3]=1ll*b[i]*k%mod,len-=k;
if(len) c[++n3]=1ll*len*b[i]%mod;
i=j;
}
}
int pos[N],tot;
int work(){
int ans=0;
for(int i=1;i<=n1;i++){
if(a[i]==m) break;
f[a[i]]=true;
ans++;
Bit.modify(a[i]);
}
int l,r,res,mid,lst,x,C;
for(int i=1;i<=n3;i++){
lst=tot=0,C=c[i];
if(Bit.query(0,mod-1)*mi[C]==Bit.query(C,mod-1+C)) continue;
while(true){
l=lst,r=mod-1,res=-1;
while(l<=r){
mid=(l+r)>>1;
if(Bit.query(lst,mid)*mi[C]!=Bit.query(lst+C,mid+C)) res=mid,r=mid-1;
else l=mid+1;
}
if(res==-1) break;
if(f[res]) pos[++tot]=res;
lst=res+1;
}
ans+=tot;
for(int j=1;j<=tot;j++){
x=add(pos[j],C);
f[x]=true,Bit.modify(x);
}
}
return ans;
}
signed main(){
freopen("operation.in","r",stdin);
freopen("operation.out","w",stdout);
mi[0]=1;
for(int i=1;i<N*2;i++) mi[i]=mi[i-1]*Base;
Eular();
IO.read_int(T);
while(T--){
IO.read_int(m),IO.read_int(n),n1=n2=0;
zero=false;
int op,x;
for(int i=1;i<=n;i++){
IO.read_int(op),IO.read_int(x);
if(op==0) a[++n1]=x;
else b[++n2]=x;
zero|=(x==0);
}
if(!n1){
printf("%d\n",m-1);
continue;
}
Init();
printf("%d\n",m-(work()+zero));
if(T) memset(f,0,sizeof f),Bit.Init();
}
return 0;
}
C.排列
原題:[PA 2022] Chodzenie po linie
題意
給定一個長度為 \(n\) 的排列 \(p\) 由它生成一張無向圖 \(G\),兩個點 \(i,j\) 之間有邊當且僅當 \(i<j\) 且 \(p_i>p_j\),邊權均為 \(1\),記 \(dis(x,y)\) 表示 \(G\) 中兩點間的最短路,特殊的,如果 \(x,y\) 不連通 \(dis(x,y)=0\),請對每個 \(x\in [1,n]\) 求 \(\sum_{y=1}^n dis(x,y)\)。
數據范圍: \(1\le n \le 2\times 10^5\)。
題解
首先解決連通性問題,不難證明,如果有一個 \(i\) 滿足 \(\forall j \in [1,i],p_j < p_i\) 那 \([1,i]\) 和 \([i+1,n]\) 之間一定不可能相互到達,找出每個這樣的 \(i\) 就可以把原排列劃分成若干段連通的區間。
下面假設整個排列連通。
考慮如何計算單個 \(i\) 的答案,我們只考慮左邊對 \(i\) 的貢獻,右半邊只需要把排列翻轉再做一次即可。
直接算最短路顯然不好算,考慮改為計算有多少個最短路 \(>=t\),那么答案就是:\(\sum_{t\ge 1} \sum_j [dis(i,j)\ge t]\)。
首先 \(t=1\) 答案顯然是 \(i-1\),對于 \(t>1\) 的情況,我們把 \((i,p_i)\) 看成一個點放到平面上考慮。
那么顯然下圖中紅色矩形內的點可以被一步到達,左下角的矩形內的點都無法被到達,他們滿足 \(j<i,p_j<p_i\)。
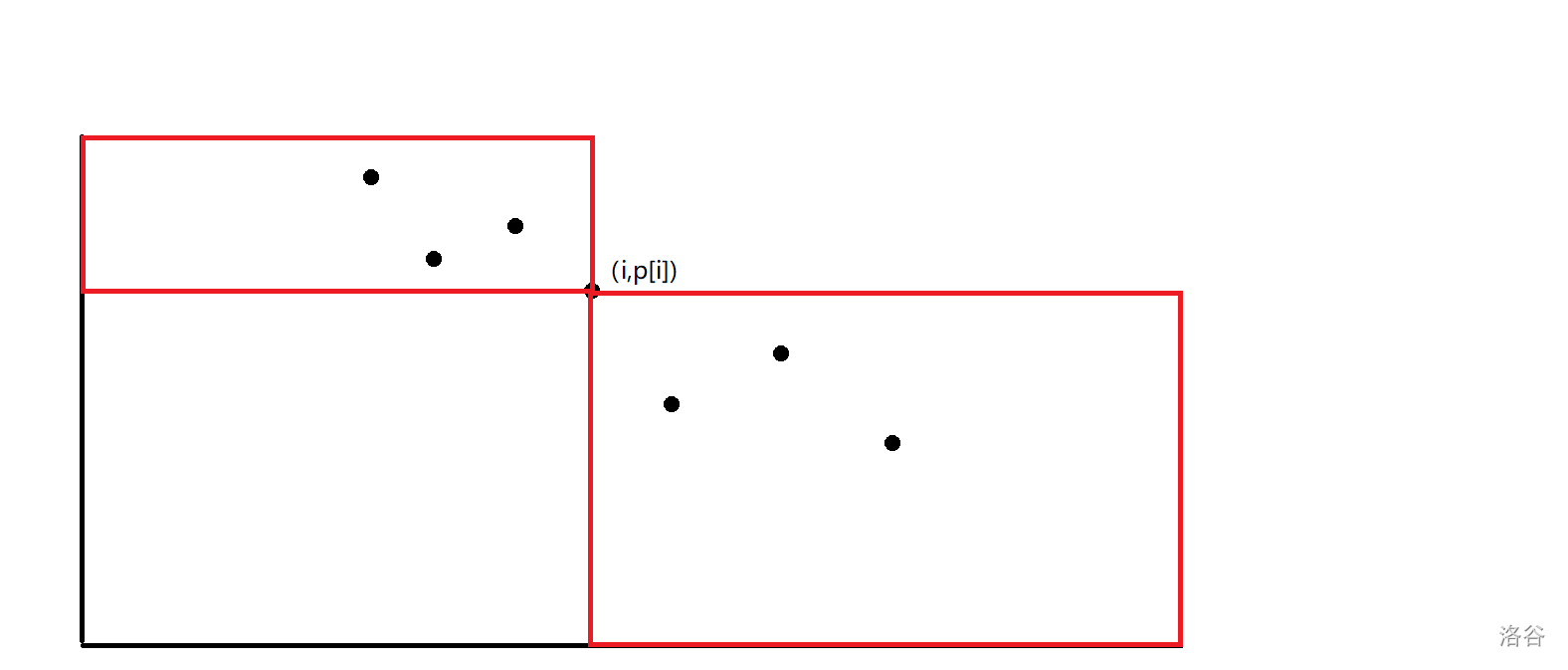
我們找到矩形 \(A\) 中最靠左的點和矩形 \(B\) 中最靠右的點,不難發現前者可以一步到達綠色矩形內的點,后者可以一步到達黃色矩形內的點,那么此時左下角那個更小的矩形就是 \(dis\ge 3\) 的點。
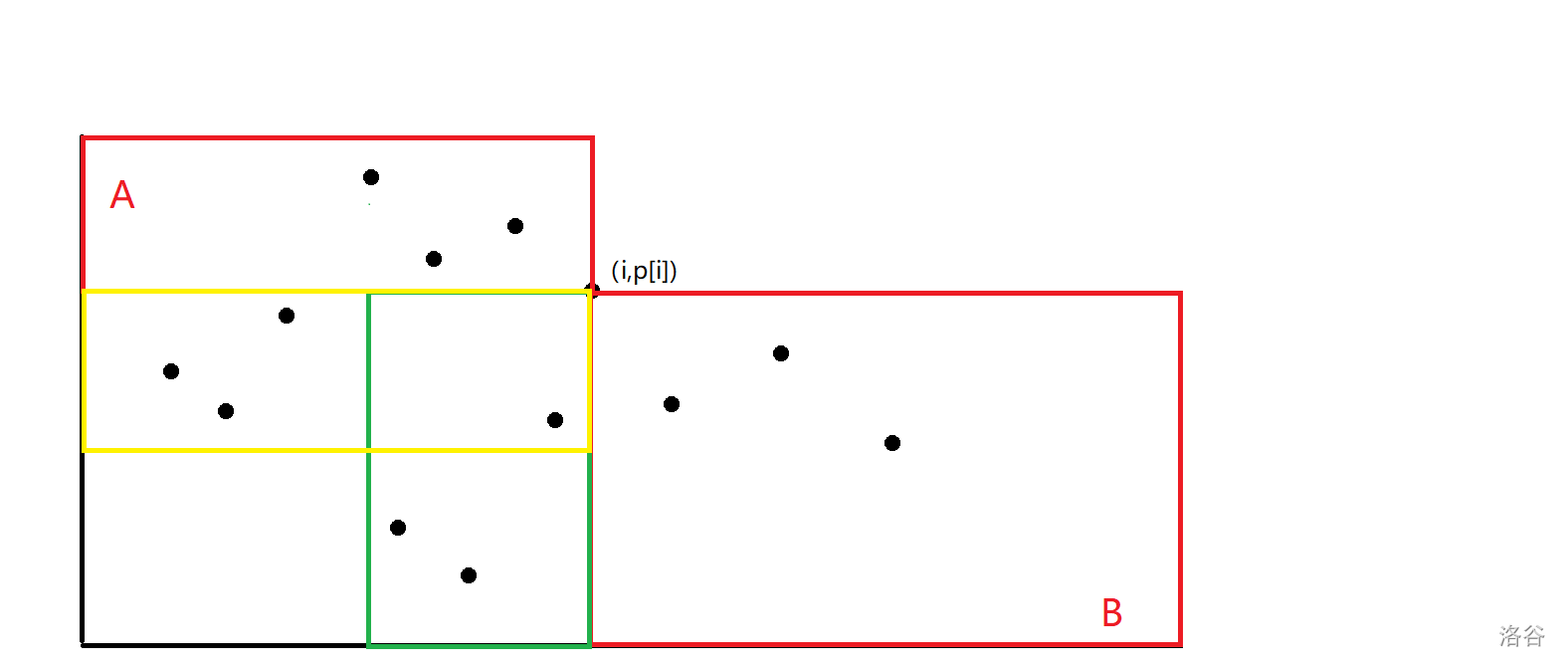
同理,我們繼續找到黃色矩形中最靠左的點和綠色矩形中最靠下的點,就可以得到 \(dis\ge 4\) 的點的范圍了,即圖中的紫色矩形。
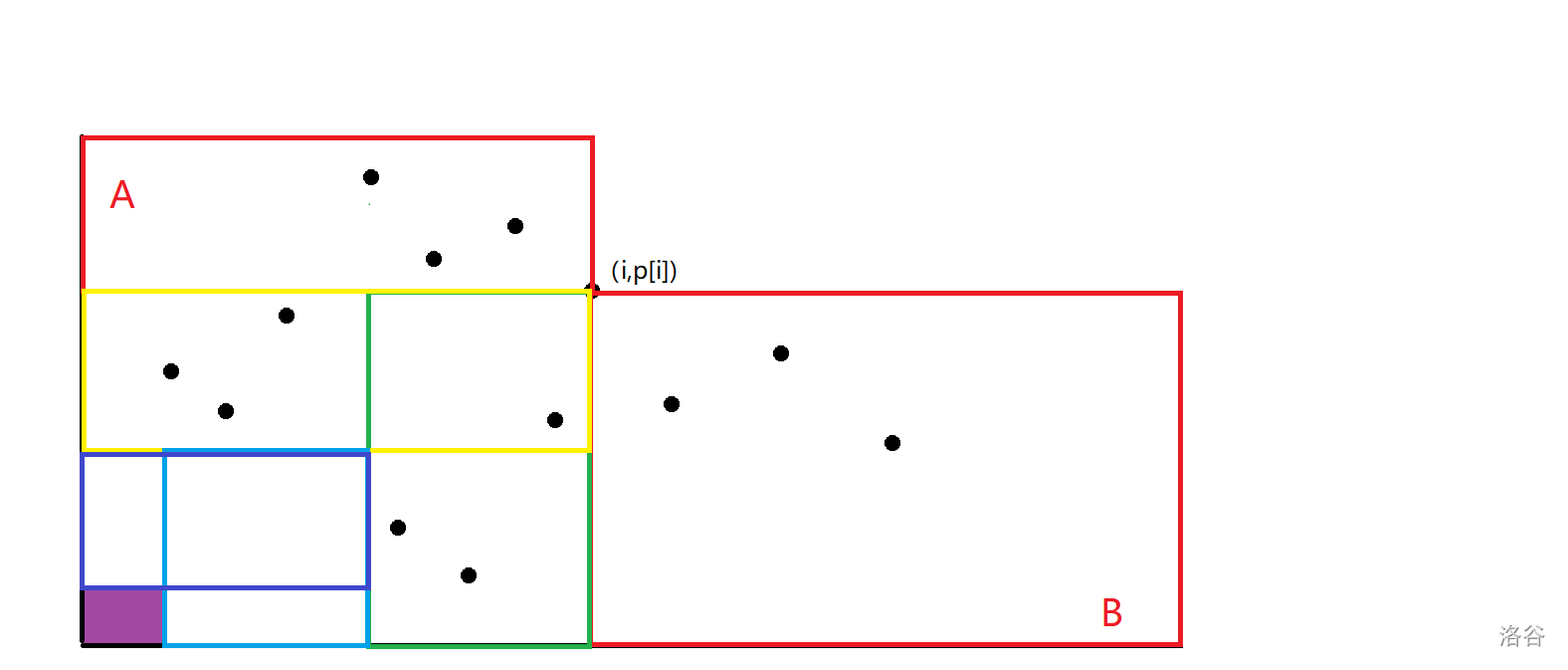
會發現對于每個 \(t\) 的答案都是一個矩形求和,設 \((a_t,b_t)\) 表示 \(t\) 的答案是所有滿足 \(j<a_t,p_j<p_{b_t}\) 的 \(j\) 的數量,那么根據上述過程容易發現,\((a_2,b_2)=(i,i)\),\((a_{t+1},b_{t+1})=(ls_{b_t},rs_{a_t})\),其中 \(ls_x\) 表示 \(x\) 能到達的最靠左的點,\(rs_x\) 表示 \(x\) 能到達的最靠下的點。所以你只要預處理二維前綴和就可以做到 \(O(n^2)\)。
如果把 \((x,y)\) 向 \((ls_y,rs_x)\) 連有向邊,會連出一個內向樹森林,我們要求的東西就是一條根鏈上每個點矩形和的總和,
接下來我們證明這個森林中所有會用到的點是 \(O(n\sqrt{n})\) 級別的。
根據點的生成過程不難發現有用的點 \((x,y)\) 一定滿足 \(x<y,p_x>p_y\)(除了那 \(n\) 個形如 \((i,i)\) 的點,但是他們的數量可以忽略)。所以對于一個 \(x\),我們找出所有滿足 \(y>x,p_y<p_x\) 的 \(y\),假設按照 \(p_y\) 從小到大排序后是 \(y_1,y_2,y_3,...\)。對于一個點 \((x,y_k)\) 如果 \(k\le \sqrt{n}\) 我們稱他為好點,否則為壞點。顯然好點的數量是 \(O(n\sqrt{n})\)。對于壞點 \((x,y_k)\) 他的下一步會跳到 \((ls_{y_k},y_1)\),顯然有 \(ls_{y_k}\le x,p_{y_1}\le p_{y_k} - \sqrt{n}\),因此一個壞點每跳一次都會使 \(x+p_y\) 減少至少 \(O(\sqrt{n})\),因為我們是從 \(n\) 個 \((x,x)\) 開始跳的,所以初始 \(x+p_y\) 的總和是 \(O(n^2)\),而 \(x+p_y\) 顯然不會增加,因此所有會跳到的壞點的數量是 \(O(n\sqrt{n})\) 的,而它一定大于等于有用的壞點數量。證畢。
有了這個結論之后就好做很多了,假設我們已經得到了這 \(O(n\sqrt{n})\) 個點,那么就有 \(O(n)\) 次單點加,\(O(n\sqrt{n})\) 次矩形求和,我們對 \(x\) 掃描線,維護 \(y\) 這一維,變成區間求和,用分塊平衡一下做到 \(O(n\sqrt{n})\)。同時注意到樹上 \((x,y)\) 的父親 \((x',y')\) 一定滿足 \(x'\le x\) ,也就是說父親會先被計算到,所以我們不需要去把樹建出來直接讓兒子繼承父親的貢獻就可以得到兒子的答案了。
接下來說如和得到所有有用的點。
實測你對每個 \((i,i)\) 暴力的跑出所有點并用 unordered_map 記錄是否被訪問過會被卡常。(反正我被卡了)
因為 \((x,y)\) 的父親 \((x',y')\) 一定滿足 \(x'\le x\),所以我們可以按照 \(x\) 從大往小來加點,初始時每個 \(x\) 的隊列中只有 \((x,x)\) 一個點,當掃到 \(x\) 時,遍歷他隊列中的每個點 \((x,y)\) 把 \((ls_y,rs_x)\) 加入到 \(ls_y\) 的集合中,同時容易證明 \(j\) 越小 \(p_{rs_j}\) 一定越小,也就是說此時的 \(rs_x\) 一定是 \(ls_y\) 隊列中 \(p\) 值最小的(初始的那一個元素特判即可),因此我們直接看隊尾和放進去的數是否一樣即可去重。
總復雜度 \(O(n\sqrt{n})\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define LL long long
using namespace std;
const int N=2e5+5,B=450;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
namespace Work{
int n,p[N];
LL res[N];
struct SegmentTree{
struct node{
int l,r,ming;
}t[N<<2];
void pushup(int p){
t[p].ming=min(t[p<<1].ming,t[p<<1|1].ming);
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r,t[p].ming=n+1;
if(l==r) return;
int mid=(l+r)>>1;
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
}
void change(int p,int x,int val){
if(t[p].l==t[p].r){
t[p].ming=val;
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid) change(p<<1,x,val);
else change(p<<1|1,x,val);
pushup(p);
}
int ask(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r) return t[p].ming;
int res=n+1,mid=(t[p].l+t[p].r)>>1;
if(l<=mid) res=min(res,ask(p<<1,l,r));
if(r>mid) res=min(res,ask(p<<1|1,l,r));
return res;
}
}Seg;
struct DS{
int L[N],R[N],id[N],s[N],pre[B];
void Init(){
for(int i=1;i<=n;i++){
id[i]=(i+B-1)/B,R[id[i]]=i;
if(i%B==1) L[id[i]]=i;
s[i]=0;
}
for(int i=1;i<=id[n];i++) pre[i]=0;
}
void add(int x,int val){
for(int i=x;i<=R[id[x]];i++) s[i]+=val;
for(int i=id[x];i<=id[n];i++) pre[i]+=val;
}
int query(int l,int r){
if(l==L[id[l]]) return s[r];
else return s[r]-s[l-1];
}
int ask(int l,int r){
if(l>r) return 0;
if(id[l]==id[r]) return query(l,r);
return query(l,R[id[l]])+query(L[id[r]],r)+pre[id[r]-1]-pre[id[l]];
}
}ds;
int ls[N],rs[N];
struct P{
int y,fa;
LL ans;
};
vector<P> v[N];
void Init(){
for(int i=1;i<=n;i++) v[i].clear();
Seg.build(1,1,n);
ds.Init();
}
void work(int op){
Init();
for(int i=1;i<=n;i++){
Seg.change(1,p[i],i);
ls[i]=Seg.ask(1,p[i],n);
}
int pos=n;
for(int i=n;i>=1;i--){
if(p[i]<p[pos]) pos=i;
rs[i]=pos;
}
for(int x=1;x<=n;x++) v[x].push_back({x,0,0});
for(int x=n;x>=1;x--){
for(int i=0;i<v[x].size();i++){
int y=v[x][i].y;
if(rs[x]!=v[ls[y]].back().y&&rs[x]!=ls[y]) v[ls[y]].push_back({rs[x],0,0});
v[x][i].fa=v[ls[y]].size()-1;
}
}
for(int x=1;x<=n;x++){
//此時 v[x] 中的 y 是按照 p[y] 降序排的,但是在計算答案的時候父親的 p[y'] <= 當前節點的 p[y],需要在之前被計算到,所以要把 y 按照 p[y] 升序排。
for(int i=v[x].size()-1;i>=0;i--){
int y=v[x][i].y;
v[x][i].ans=v[ls[y]][v[x][i].fa].ans+ds.ask(1,p[y]-1);
if(x==y){
if(op) res[n-x+1]+=v[x][i].ans+x-1;
else res[x]+=v[x][i].ans+x-1;
}
}
ds.add(p[x],1);
}
}
void Main(){
for(int i=1;i<=n;i++) res[i]=0;
work(0);
for(int i=1;i<=n;i++) p[i]=n-p[i]+1;
reverse(p+1,p+n+1);
work(1);
for(int i=1;i<=n;i++) printf("%lld ",res[i]);
}
}
int n,a[N];
signed main(){
freopen("permutation.in","r",stdin);
freopen("permutation.out","w",stdout);
n=read();
vector<int> pos;
int maxn=0;
for(int i=1;i<=n;i++){
a[i]=read();
maxn=max(maxn,a[i]);
if(maxn==i) pos.push_back(i);
}
int lst=1;
for(int x:pos){
Work::n=0;
for(int i=lst;i<=x;i++) Work::p[++Work::n]=a[i]-(lst-1);
lst=x+1;
Work::Main();
}
puts("");
return 0;
}
Day2 模擬賽
A.火力全開
題意
有 \(n\) 個敵人,每個敵人有兩個屬性 \(a_i\) 和 \(b_i\) 表示血條和抗爆能力。
你可以進行若干輪攻擊,每次選擇一下兩種方式中的一種:
- 指定一名敵人,花費 \(1\) 的代價,并對他造成 \(1\) 點真實傷害。
- 用一枚炸彈,對所有敵人造成一次爆炸傷害。
其中對于第 2 中攻擊方式,你初始有 \(m\) 枚炸彈,第 \(i\) 枚炸彈的代價是 \(c_i\),爆炸傷害是 \(d_i\),每次你都可以選擇一枚使用,每枚炸彈只能使用一次。
當第 \(i\) 個敵人受到 \(a_i\) 點真實傷害,或者受到 \(k\) 次大于等于 \(b_i\) 的爆炸傷害,他就會死亡。
現在你需要求出最少花費多少的代價可以殺死所有敵人。
當然這太簡單了,所以你先還需要支持 \(q\) 次修改,每次修改形如 op x y z,如果 \(op=1\) 表示令 \(y \to a_x,z \to b_x\),否則表示令 \(y\to c_x,z\to d_x\)。
你需要在每次修改完之后求出答案,修改之間不獨立。
數據范圍:\(1\le n,m,q\le 2.5\times 10^5,1\le k \le 10^4,kq\le 5\times 10^5,1\le a_i,b_i,c_i,d_i,y,z \le 10^9\)。
題解
首先有一個顯然的貪心,枚舉 \(k\) 個炮彈中最小的爆炸傷害 \(d\),那么此時的總代價是 \(\sum_{b_i>d}a_i + S(k,d)\),\(S(k,d)\) 表示爆炸傷害 \(\ge d\) 的炮彈中代價前 \(k\) 小的和。
但是這個貪心不太好直接維護。
注意到數據范圍中有一個很特殊的 \(kq\le 5\times 10^5\),這啟發我們去維護某些大小為 \(O(k)\) 的信息。
先把所有 \(d_i\) 以及 \(op=2\) 時的 \(z\) 離散化,建立值域線段樹。
對于線段樹上的每個節點 \(p\),我們去維護 \(mn_{p,i}\) 表示 \(p\) 所代表的區間中代價第 \(i\) 小的炮彈的代價,以及 \(f_{p,i}\) 表示從區間中選出 \(i\) 枚炸彈時的最小代價總和。那么答案就是 \(\min(\sum_{i=1}^n a_i,f_{1,k})\)。容易發現這兩個數組的長度都是 \(O(\min(k,siz))\) 的,\(siz\) 表示 \(p\) 所代表的區間中實際有的炮彈數量。
考慮 \(f\) 的轉移:
- \(i\) 個炮彈全來自右兒子:\(f_{rs,i} \to f_{p,i}\)。
- \(j\) 個炮彈來自左兒子,其余來自右兒子:\(f_{ls,j} + suma_{rs} + pre_{rs,i-j} \to f_{p,i}\),\(suma\) 表示區間中的敵人的 \(\sum a_i\),\(pre_{rs,i}=\sum_{j=1}^i mn_{rs,j}\)。
對于第 2 個轉移,\(suma_{rs}\) 是常量不去管,記 \(w(j,i)=f_{ls,j} + pre_{rs,i-j}\),容易證明他滿足四邊形不等式,所以第 2 個轉移可以決策單調性優化到 \(O(\min(siz,k)\log \min(siz,k))\)。
故線段樹的 pushup 的復雜度是 \(O(\min(siz,k)\log \min(siz,k))\)。
對于修改操作就是一個簡單的單點修改,不贅述。
關于總時空復雜度(\(n\) 代表線段樹值域大小):
- 空間復雜度:因為線段樹的每個節點開的數組大小不是 \(O(k)\) 而是 \(O(\min(siz,k))\) 所以線段樹的每一層的空間是 \(O(n)\) 的,整顆線段樹的總空間是 \(O(n\log n)\)。
- 時間復雜度:類似的可以證明線段樹建樹的復雜度是 \(O(n\log k \log n)\),而一次修改操作會
pushup\(O(\log n)\) 次,所以修改的總復雜度是 \(O(qk\log k\log n)\)。
code
#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N=250000+5;
const LL inf=3e14;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,T,k,a[N],b[N],c[N],d[N],dis[N<<1],cnt;
LL Sum;
int Dis(int x){return lower_bound(dis+1,dis+cnt+1,x)-dis;}
struct Que{
int op,x,y,z;
}q[N];
vector<int> v[2][N<<1];
struct SegmentTree{
struct node{
int l,r,siz;
LL sum;
vector<LL> mn,pre,f;
void Init(){
siz=min(k,(int)v[0][l].size()),sum=0;
mn.resize(siz+1),f.resize(siz+1),pre.resize(siz+1);
sort(v[0][l].begin(),v[0][l].end(),[&](int x,int y){return c[x]<c[y];}); //注意要先對 vector 排序在賦值給 mn,而不能先賦值再對 mn 排序
for(int i=0;i<siz;i++) mn[i+1]=c[v[0][l][i]];
for(int id:v[1][l]) sum+=a[id];
f[0]=sum;
for(int i=1;i<=siz;i++) f[i]=f[i-1]+mn[i],pre[i]=pre[i-1]+mn[i];
}
}t[N<<4];
LL Pre(int p,int x){ return (x<=t[p].siz)?t[p].pre[x]:inf; }
void solve(int p,int l,int r,int L,int R){
if(l>r) return;
int mid=(l+r)>>1,opt=L,ls=p<<1,rs=p<<1|1;
LL res=t[rs].sum+t[ls].f[L]+Pre(rs,mid-L);
for(int i=L+1;i<=min(R,mid);i++){
if(t[rs].sum+t[ls].f[i]+Pre(rs,mid-i)<res){
opt=i;
res=t[rs].sum+t[ls].f[i]+Pre(rs,mid-i);
}
}
t[p].f[mid]=res;
solve(p,l,mid-1,L,opt),solve(p,mid+1,r,opt,R);
}
void pushup(int p){
int ls=p<<1,rs=p<<1|1;
t[p].siz=min(k,t[ls].siz+t[rs].siz);
t[p].sum=t[ls].sum+t[rs].sum;
t[p].mn.resize(t[p].siz+1),t[p].pre.resize(t[p].siz+1),t[p].f.resize(t[p].siz+1);
int i=1,j=1;
for(int x=1;x<=t[p].siz;x++){
if(i<=t[ls].siz&&(j>t[rs].siz||t[ls].mn[i]<t[rs].mn[j])) t[p].mn[x]=t[ls].mn[i++];
else t[p].mn[x]=t[rs].mn[j++];
t[p].pre[x]=t[p].pre[x-1]+t[p].mn[x];
}
solve(p,0,t[p].siz,0,t[ls].siz);
for(int i=0;i<=min(t[rs].siz,t[p].siz);i++) t[p].f[i]=min(t[p].f[i],t[rs].f[i]);
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r;
if(l==r){
t[p].Init();
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
pushup(p);
}
void update(int p,int x){
if(x==0) return;
if(t[p].l==t[p].r){
t[p].Init();
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid) update(p<<1,x);
else update(p<<1|1,x);
pushup(p);
}
}Seg;
void Init(){
sort(dis+1,dis+cnt+1);
cnt=unique(dis+1,dis+cnt+1)-dis-1;
for(int i=1;i<=n;i++) b[i]=Dis(b[i])-1,v[1][b[i]].push_back(i);
for(int i=1;i<=m;i++) d[i]=Dis(d[i]),v[0][d[i]].push_back(i);
for(int i=1;i<=T;i++){
if(q[i].op==1) q[i].z=Dis(q[i].z)-1;
else q[i].z=Dis(q[i].z);
}
Seg.build(1,1,cnt);
}
void Add(int x,int op,int pos){
v[op][pos].push_back(x);
Seg.update(1,pos);
}
void Del(int x,int op,int pos){
for(vector<int>::iterator it=v[op][pos].begin();it!=v[op][pos].end();++it){
if((*it)==x){
v[op][pos].erase(it);
break;
}
}
Seg.update(1,pos);
}
signed main(){
freopen("fire.in","r",stdin);
freopen("fire.out","w",stdout);
n=read(),m=read(),T=read(),k=read();
for(int i=1;i<=n;i++) a[i]=read(),b[i]=read(),Sum+=a[i];
for(int i=1;i<=m;i++) c[i]=read(),d[i]=read(),dis[++cnt]=d[i];
for(int i=1;i<=T;i++){
int op=read(),x=read(),y=read(),z=read();
q[i]={op,x,y,z};
if(op==2) dis[++cnt]=z;
}
Init();
for(int i=1;i<=T;i++){
if(q[i].op==1){
Del(q[i].x,1,b[q[i].x]);
Sum-=a[q[i].x];
a[q[i].x]=q[i].y,b[q[i].x]=q[i].z;
Sum+=a[q[i].x];
Add(q[i].x,1,q[i].z);
}
else{
Del(q[i].x,0,d[q[i].x]);
c[q[i].x]=q[i].y,d[q[i].x]=q[i].z;
Add(q[i].x,0,q[i].z);
}
printf("%lld\n",min(Sum,Seg.t[1].f[k])); //注意 Seg.t[1].sum!=Sum
}
return 0;
}
閑話
關于我大樣例沒過,結果一交 AC 這件事。數據沒有大樣例強是這樣的。(這個數據甚至還是在賽時加了兩個 hack 的)。
B.異或癥測試 3
題意
給定一個大小為 \(n\) 的集合 \(B\) 和一個數 \(X\),問集合 \(S=\{1,2,...,X \}\) 有多少非空子集 \(T\) 滿足 \(B\) 是 \(T\) 的線性基。對 \(998244353\) 取模。
稱 \(B\) 是 \(T\) 的線性基當且僅當 \(T\) 中所有元素都可以由 \(B\) 中的若干元素異或得到,且 \(B\) 是所有滿足條件的集合中大小最小的。(當然一個集合的線性基可能不止一個)
\(B\) 中的數以及 \(X\) 都以一個 \(m\) 位二進制數的形式給出。
數據范圍:\(1\le n,m\le 2\times 10^3\)。
C.樹上鄰鄰域數點
題意
這是一道交互題。
給定一課 \(n\) 個點的樹,節點編號 \(\in [0,n-1]\),每個點有一個未知的屬于 \([0,31]\) 的點權,每次你可以向交互庫詢問 \((x,d,v)\) 表示樹上與 \(x\) 距離恰好為 \(d\) 的點中有多少個點的點權 \(\le v\),同時你需要保證每次詢問的 \(v\) 不小于一個的給定的數 \(L\)。
你需要在 \(2.5 \times 10^5\) 次詢問內求出每個點的點權。
數據范圍:\(n=50000,0\le L\le 2\)。
附上附件中交互庫的使用方法:
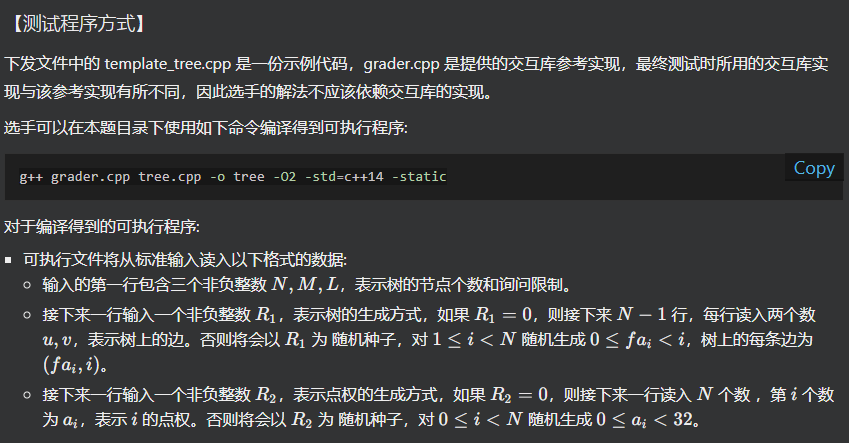
Day4 模擬賽
A.樹
原題:Equal Trees。
題意
給你兩棵編號從 \(1\) 到 \(n\),以 \(1\) 為根的有根樹,定義一次操作形如:選擇一棵樹以及一個點 \(x\)(\(x\ne 1\)),把 \(x\) 的所有兒子接到 \(fa_x\) 上,并刪除 \(x\) 以及和他相連的所有邊。
定義兩棵有根樹是相同的當且僅當他們節點編號的集合相同且相同編號的點的父親在兩棵樹中的編號相同,問最少操作幾次才能使兩棵樹變成相同的。
注意:相同 \(\ne\) 同構。
數據范圍:\(1\le n \le 40\)。
題解
正難則反,考慮求出最多保留多少點。
容易發現一個保留的點集 \(S\) 合法當且僅當不存在 \(x,y \in S\),且 \(x\) 在其中一棵樹上是 \(y\) 的祖先但是在另一棵樹上不是(\(y\) 是 \(x\) 的祖先同理)。
所以我們按照這個規則連邊,答案就是這張無向圖上的最大獨立集。
因為 \(n\) 很小,所以 meet in the middle 即可,我的復雜度是 \(O(n2^{\frac{n}{2}})\)。
code
#include<bits/stdc++.h>
#define DEBUG puts("-------------------------")
using namespace std;
const int N=(1<<20)+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,fa[2][50],tmp[2][50],dep[2][50];
vector<int> G[2][50];
void dfs(int u,int op){
dep[op][u]=dep[op][fa[op][u]]+1;
for(int v:G[op][u]){
if(v==fa[op][u]) continue;
fa[op][v]=u;
dfs(v,op);
}
}
int LCA(int x,int y,int op){
if(dep[op][x]>dep[op][y]) swap(x,y);
while(dep[op][y]>dep[op][x]) y=fa[op][y];
while(x!=y) x=fa[op][x],y=fa[op][y];
return x;
}
struct Graph{
int tot,head[50],to[2000],Next[2000];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
bool flag[50],stater[50];
int f[N],g[N];
void dfs(int u,int Max,int cnt){
if(u==Max+1){
if(Max==n/2){
int S=0;
for(int i=n/2+1;i<=n;i++) if(!flag[i]) S|=(1<<(i-n/2-1));
f[S]=max(f[S],cnt);
}
else{
int S=0;
for(int i=n/2+1;i<=n;i++) if(stater[i]) S|=(1<<(i-n/2-1));
g[S]=max(g[S],cnt);
}
return;
}
dfs(u+1,Max,cnt);
if(!flag[u]){
vector<int> vec;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(!flag[v]) vec.push_back(v),flag[v]=true;
}
stater[u]=true;
dfs(u+1,Max,cnt+1);
for(int v:vec) flag[v]=false;
stater[u]=false;
}
}
void work(){
dfs(1,n/2,0),dfs(n/2+1,n,0);
for(int i=0;i<=n-n/2-1;i++){
for(int S=0;S<(1<<(n-n/2));S++){
if(S>>i&1){
g[S]=max(g[S],g[S^(1<<i)]);
}
}
}
int ans=0;
for(int S=0;S<(1<<(n-n/2));S++) ans=max(ans,f[S]+g[S]);
printf("%d\n",2*n-2*ans);
}
}T;
signed main(){
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
n=read();
for(int op=0;op<=1;op++)
for(int i=1;i<n;i++){
int u=read(),v=read();
G[op][u].push_back(v),G[op][v].push_back(u);
}
dfs(1,0),dfs(1,1);
for(int i=2;i<=n;i++){
for(int j=i+1;j<=n;j++){
int x=LCA(i,j,0),y=LCA(i,j,1);
if((x==i&&y!=i)||(x==j&&y!=j)||(y==i&&x!=i)||(y==j&&x!=j)){
T.add(i,j),T.add(j,i);
}
}
}
T.work();
return 0;
}
B.序列
原題:[ARC066F] Contest with Drinks Hard
題意
給你一個長度為 \(n\) 的序列 \(a\),和一個正整數 \(C\) 求:
你還需要支持 \(m\) 次修改,每次修改形如 x,y 表示將 \(a_x\) 修改為 \(y\) 之后的答案,修改之間互相獨立。
你需要求出初始以及每次修改之后總共 \(m+1\) 個答案。
數據范圍:\(1\le n \le 3\times 10^5,0\le m \le 3\times 10^5,1\le C\le 10^5,0\le a_i,y \le 10^9\)。
題解
不難設計出 DP,\(f_i\) 表示第 \(i\) 個數不選,前 \(i\) 個數的最大權值,轉移如下:
\(f_i = \max_{j=0}^{i-1} (f_j+\binom{i-j}{2} C-pre_{i-1}+pre_j)\)。
不難發現可以用斜率優化把復雜度降下來。
對于單點修改的題目,有一個經典套路是把前后拼起來,所以我們再預處理出來 \(g_i\) 表示從后往前考慮,不選第 \(i\) 個數,\([i,n]\) 的最大權值,以及 \(h_x\) 表示選第 \(i\) 個數時全局的答案。
那么當把 \(a_x\) 修改為 \(y\) 則答案就是 \(\max(f_x+g_x,h_x+a_x-y)\)。
其中 \(g\) 的轉移如 \(f\),主要看 \(h\) 的轉移。
暴力轉移的話,我們可以枚舉 \(i\) 前面和后面第一個沒選的位置 \(p\) 和 \(q\),那么有轉移:\(f_p+g_q+\binom{q-p}{2} C-pre_{q-1}+pre_p\)。
注意到這個式子跟 \(i\) 無關,對 \(p,q\) 的要求只有先后順序,所以考慮分治,具體的,當考慮到分治區間 \([l,r]\) 時,我們求出所有 \(p\in [l-1,mid],q\in [mid+1,r+1]\) 的 \(p,q\) 的貢獻,以左半邊為例,我們枚舉 \(p\in [l-1,mid]\) 用斜率優化求出此時最優的答案,然后貢獻到區間 \([p+1,mid]\)。右半邊同理。
因為這個斜率優化的斜率是單調的,所以可以用雙指針優化到線性,因此分治的復雜度是 \(O(n\log n)\)。
復雜度是 \(O(n\log n+q)\)。
code
#include<bits/stdc++.h>
#define DEBUG puts("-------------------------")
#define int long long
using namespace std;
const int N=3e5+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,C,a[N],pre[N],f[N],g[N],h[N];
int st[N],top;
int x(int j,int op){return 2*C*j;}
int y(int j,int op){
if(op==0) return 2*f[j]+C*j*j+C*j+2*pre[j];
else return 2*g[j]+C*j*j-C*j-2*pre[j-1];
}
bool check(int mid,int k,int op){return (y(st[mid+1],op)-y(st[mid],op))<k*(x(st[mid+1],op)-x(st[mid],op));}
int find(int k){
int l=1,r=top-1,mid,res=top;
while(l<=r){
mid=(l+r)>>1;
if(check(mid,k,0)) r=mid-1,res=mid;
else l=mid+1;
}
return st[res];
}
void Insert(int i,int op){
while(top>=2 && (__int128)(y(st[top],op)-y(st[top-1],op)) * (x(i,op)-x(st[top],op)) < (__int128)(x(st[top],op)-x(st[top-1],op)) * (y(i,op)-y(st[top],op)) ) top--;
st[++top]=i;
}
void work(){
for(int i=1;i<=n+1;i++) pre[i]=pre[i-1]+a[i];
int ans=0;
f[0]=0;
top=0;
st[++top]=0;
for(int i=1;i<=n+1;i++){
int j=find(i);
f[i]=(y(j,0)-i*x(j,0)-C*i+C*i*i-2*pre[i-1])/2;
Insert(i,0);
}
}
int calc(int p,int q){return f[p]+g[q]+C*((q-p)*(q-p-1))/2-pre[q-1]+pre[p];}
int tmp[N];
void solve(int l,int r){
if(l==r){
h[l]=max(h[l],calc(l-1,r+1));
return;
}
int mid=(l+r)>>1;
top=0;
for(int p=l-1;p<=mid;p++) Insert(p,0);
for(int q=mid+2,R=top;q<=r+1;q++){
while(R>1&&check(R-1,q,0)) R--;
tmp[q-1]=calc(st[R],q);
}
for(int i=r-1;i>=mid+1;i--) tmp[i]=max(tmp[i+1],tmp[i]);
for(int i=mid+1;i<=r;i++) h[i]=max(h[i],tmp[i]);
top=0;
for(int q=mid+1;q<=r+1;q++) Insert(q,1);
for(int p=l-1,R=top;p<=mid-1;p++){
while(R>1&&check(R-1,p,1)) R--;
tmp[p+1]=calc(p,st[R]);
}
for(int i=l+1;i<=mid;i++) tmp[i]=max(tmp[i],tmp[i-1]);
for(int i=l;i<=mid;i++) h[i]=max(h[i],tmp[i]);
solve(l,mid),solve(mid+1,r);
}
void Init(){
work();
reverse(a+1,a+n+1);
for(int i=0;i<=n+1;i++) tmp[i]=f[i];
memset(f,0,sizeof f);
work();
reverse(a+1,a+n+1);
for(int i=0;i<=n+1;i++) g[i]=f[n+1-i];
for(int i=0;i<=n+1;i++) f[i]=tmp[i];
for(int i=1;i<=n+1;i++) pre[i]=pre[i-1]+a[i];
memset(h,-0x3f,sizeof h);
solve(1,n);
}
signed main(){
freopen("sequence.in","r",stdin);
freopen("sequence.out","w",stdout);
n=read(),m=read(),C=read();
for(int i=1;i<=n;i++) a[i]=read();
Init();
printf("%lld\n",f[n+1]);
for(int i=1;i<=m;i++){
int x=read(),y=read();
printf("%lld\n",max(f[x]+g[x],h[x]+a[x]-y));
}
return 0;
}
C.棧
有三個棧 \(S1,S2,S3\) 初始時 \(S1\) 自頂向下是 \(p_1,p_2,p_3,...,p_n\)(保證 \(p\) 是排列),\(S2,S3\) 為空,你可以進行若干次操作,每次操作有兩種選擇:
- 選擇一個數 \(x\le A\) 把 \(S1\) 棧頂的 \(x\) 個數作為一個整體放入 \(S2\)。(即不改變相對順序)。
- 選擇一個數 \(x\le B\) 把 \(S2\) 棧頂的 \(x\) 個數作為一個整體放入 \(S3\)。(即不改變相對順序)。
現在需要讓 \(S3\) 自頂向下是 \(1,2,3,...n\) 請構造方案或報告無解。
多測。
數據范圍:\(1\le \sum n\le 10^6,1\le A,B\le n\) 且 \(p\) 是排列。
Day5 模擬賽
A.圖上的游戲
題意
小 A 和小 B 在一張 n 個點,m 條邊的有向圖上玩游戲,初始每個點有點權,范圍在 \([0,2]\),兩人輪流操作,小 A 先手。一個人操作時需要選擇一個點權為 \(2\) 的點并把它的點權修改為 \(0/1\)。當圖上沒有點權為 \(2\) 的點時游戲結束,此時小 A 的分數為圖上滿足 \(c_u=0,c_v=1\) 的邊 \(u\to v\) 的數量,小 B 的分數是 \(c_u=1,c_v=0\) 的邊 \(u\to v\) 的數量。定義此時這張圖的權值 \(Z=\) 小 A 的分數 \(-\) 小 B 的分數。小 A 希望讓 \(Z\) 盡量大,小 B 希望讓 \(Z\) 盡量小,問兩人都絕頂聰明的情況下最終的 \(Z\) 會是多少。
觀戰者小 C 給了你一個長度為 \(n\) 的序列 \(c_1,c_2,...,c_n\) 以及一個數 \(m\),現在需要你對每個 \((N,M)\) 滿足 \(1\le N \le n,1\le M \le m\) 求出:
對于一張 \(N\) 個點,每個點的初始點權是 \(c_1,c_2,...,c_N\) 的圖,隨機連 \(M\) 條邊(允許重邊和自環),所有 \(n^{2m}\) 種連邊方案的最終權值 \(Z\) 的和。
數據范圍:\(1\le n,m\le 50,c_i \in {0,1,2}\)。
題解
先考慮對于一張給定的圖怎么求最終權值 \(Z\)。
由于現在貢獻是在邊上的,但是操作的是點,所以考慮把貢獻轉移到點上。具體的,對于一條邊 \(u\to v\) 如果 \(c_u=0\) 就認為 \(u\) 在這條邊的貢獻是 \(1\) 否則是 \(-1\),如果 \(c_v=1\) 則認為 \(v\) 在這條邊的貢獻是 \(1\) 否則是 \(-1\)。
容易證明,此時圖上所有點的貢獻和就是 \(2Z\)。
而對于權值為 \(2\) 的點,設他的出度減去入度為 \(d\),那么如果它的點權修改為 \(0\),則貢獻就是 \(d\),否則就是 \(-d\)。因為一個人操作的時候可以把點權為 \(2\) 的點修改為任意權值,因此如果小 A 操作,那最后這個點的貢獻就是 \(|d|\),如果是小 B 操作,最后這個點的貢獻就是 \(-|d|\)。因此兩人的最優策略就是把所有權值為 \(2\) 的點按照 \(d\) 從大到小排序之后輪流取,奇數位貢獻為 \(|d|\),偶數位貢獻為 \(-|d|\)。
最后把原先點權就是 \(0/1\) 的點的貢獻加上再除個 \(2\) 就是 \(Z\)。
根據這個計算方法,我們還可以發現一個性質,記 \(ans(N,M)\) 表示題目中要你求的對于 \((N,M)\) 的答案,那么那些原先權值就是 \(0/1\) 的點對 \(ans(N,M)\) 的貢獻一定是 \(0\)。
這是因為這些點的貢獻只跟他們的出度-入度有關,而我們只需要把一張圖的邊全部反向就可以使他們的貢獻取反(容易證明如果這張圖的邊全部取反之后和原圖是一樣的,那么此時每個點的貢獻一定全是 \(0\),因此不需要考慮這種情況)。
所以我們只需要考慮權值為 \(2\) 的點的貢獻。
如果我們已經確定了每個點的出度和入度,那么方案數就是兩個可重集排列數的乘積。所以 DP 過程就是給每個點確定出度和入度。
因為權值為 \(0/1\) 的點和權值為 \(2\) 的點是相對獨立的,可以分開考慮。(權值為 \(0/1\) 的點雖然本身不產生貢獻但是會對方案數產生影響)
對于權值為 \(0/1\) 的點,DP 是簡單的,設 \(f_{i,j,k}\) 表示給 \(i\) 個點分配 \(j\) 個出度和 \(k\) 個入度的方案數,轉移顯然。
對于權值為 \(2\) 的點,注意到我們最開始的那個貪心過程要求我們對 \(|d|\) 從大到小排序,所以我們 DP 的時候需要按照 \(|d|\) 從大到小加入,不難發現這其實是一個高維背包,二元組 \((x,y)\)(\(x\) 表示出度,\(y\) 表示入度)就表示一個物品,我們需要按照 \(|x-y|\) 從大到小把物品加入背包。那么設 \(g_{i,j,u,v}\) 表示考慮到第 \(i\) 個物品,分配了 \(j\) 個點,\(u\) 個出度,\(v\) 個入度的貢獻之和,為了輔助轉移還需要記錄 \(h_{i,j,u,v}\) 表示方案數。轉移時就去枚舉當前物品分配給了幾個點。直接做是 \(O(n^2m^4)\),但是發現轉移時有個調和級數,于是變成 \(O(n^2m^3\log m)\),稍微剪枝可過。
算答案的時候就是把兩個 DP 數組合并一下。需要注意的是在算 \(g,h\) 時我們欽定了順序,但實際上分配是隨便分配的(欽定順序只是為了方便計算貢獻),所以方案數還需要乘上一個可重集排列數。
具體實現時就是把幾個可重集排列數的分子分母拆開,分母放到 DP 里面,分子由于是定值在最后算答案的時候乘上即可。
code
#include<bits/stdc++.h>
#define DEBUG puts("-------------------------")
using namespace std;
const int N=50+5,mod=1e9+7,inv2=(mod+1)/2;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,c[N],fact[N],inv[N],cnt;
int f[N][N][N],g[2][N][N][N],h[2][N][N][N];
void add(int &x,int y){x+=y; if(x>=mod) x-=mod;}
int qp(int a,int b){
int ans=1;
while(b){
if(b&1) ans=1ll*ans*a%mod;
b>>=1,a=1ll*a*a%mod;
}
return ans;
}
struct node{
int x,y,d;
}a[N*N];
int val(int s1,int s2,int x){
if(s2&1){
if(s1&1) return mod-x;
return x;
}
return 0;
}
signed main(){
freopen("game.in","r",stdin);
freopen("game.out","w",stdout);
n=read(),m=read();
int c2=0;
for(int i=1;i<=n;i++) c[i]=read(),c2+=(c[i]==2);
fact[0]=1;
for(int i=1;i<=n;i++) fact[i]=1ll*fact[i-1]*i%mod;
inv[1]=inv[0]=1;
for(int i=2;i<=n;i++) inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
for(int i=1;i<=n;i++) inv[i]=1ll*inv[i-1]*inv[i]%mod;
f[0][0][0]=1;
for(int i=1;i<=n-c2;i++)
for(int j=0;j<=m;j++)
for(int k=0;k<=m;k++){
for(int x=0;x<=j;x++)
for(int y=0;y<=k;y++)
add(f[i][j][k],1ll*f[i-1][j-x][k-y]*inv[x]%mod*inv[y]%mod);
}
for(int x=0;x<=m;x++) for(int y=0;y<=m;y++) a[++cnt]={x,y,abs(x-y)};
sort(a+1,a+cnt+1,[&](node u,node v){return u.d>v.d;});
h[0][0][0][0]=1;
for(int i=1;i<=cnt;i++){
memset(g[i&1],0,sizeof g[i&1]);
memset(h[i&1],0,sizeof h[i&1]);
int x=a[i].x,y=a[i].y,d=a[i].d;
for(int j=0;j<=c2;j++){
for(int u=0;u<=m;u++){
for(int v=0;v<=m;v++){
if(h[i&1^1][j][u][v]){
for(int k=0;j+k<=c2&&u+k*x<=m&&v+k*y<=m;k++){
int t1=1ll*qp(1ll*inv[x]*inv[y]%mod,k)*inv[k]%mod,t2=1ll*h[i&1^1][j][u][v]*t1%mod;
add(h[i&1][j+k][u+k*x][v+k*y],t2);
add(g[i&1][j+k][u+k*x][v+k*y],(1ll*g[i&1^1][j][u][v]*t1%mod+1ll*val(j,k,d)*t2%mod)%mod);
}
}
}
}
}
}
int num1=0,num2=0;
for(int i=1;i<=n;i++){
if(c[i]<2) num1++;
else num2++;
for(int M=1;M<=m;M++){
int ans=0;
for(int j=0;j<=M;j++){
for(int k=0;k<=M;k++){
add(ans,1ll*f[num1][j][k]*g[cnt&1][num2][M-j][M-k]%mod*fact[M]%mod*fact[M]%mod*fact[num2]%mod);
}
}
printf("%d ",1ll*ans*inv2%mod);
}
puts("");
}
return 0;
}
B.修理
題意
對于一個正整數序列 \(b\) 定義它的代價為最少的操作次數使他變成全 \(0\),一次操作有兩種選擇:
- 令 \(x\) 加一。
- 選擇一個 \(b_i\) 并讓他變成 \(b_i \oplus x\)。
其中 \(x\) 是一個初始為 \(0\) 的變量。
現在給定一個長度為 \(n\) 的序列 \(a\),有 \(Q\) 次詢問,每次詢問 \([l,r]\) 表示詢問 \(a_l,a_{l+1},...,a_r\) 的代價。
強制在線。
數據范圍:\(1\le n,Q \le 2\times 10^5,1\le a_i < 2^{60}\)。
提示: 根號是沒有前途的。
題解
首先不難發現要把一個序列 \(b\) 變成全 \(0\),那么 \(x\) 至少要加到 \(2^k\),其中 \(k\) 是 \(b\) 中所有數的二進制最高位的最大值,否則沒有辦法把這一位消掉。然后對于那些 \(\le x\) 的 \(b_i\) 可以一步解決,對于那些 \(>x\) 的 \(b_i\) 可以兩步解決。
所以區間 \([l,r]\) 的答案就是 \(r-l+1+\min_{x\ge 2^k}(x+\sum_{i=l}^r[a_i>x])\)。
發現會對 \(∑_{i=l}^r[a_i>x]\) 產生貢獻的是 \([2^k+1,2^{k+1}-1]\) 中的數,所以我們可以把 \(a\) 序列按照二進制最高位分成 \(\log V\) 個子序列,每一個子序列單獨考慮。
對于二進制最高位為 \(k\) 的子序列,可以把里面的數全都減去 \(2^k\),這樣值域下界就變成了 \(1\),要求的就可以寫成:\(\min_{x\ge 0}(x+\sum_{i=l}^r[a_i>x])\)。
發現當 \(x=0\) 時 \(\min_{x\ge 0}(x+\sum_{i=l}^r[a_i>x])\) 的值是 \(r-l+1\),所以 \(x\) 一定不超過 \(r-l+1\),也就只需要考慮那些值域在 \(O(n)\) 范圍內的 \(a_i\)。(注意:雖然我們不去考慮那些 \(>n\) 的 \(a_i\) 但是他們對答案是有貢獻的,在最后算答案的時候要加上。),下面默認所有 \(a_i\) 的值域是 \([1,n]\)。
進一步轉換,\(\min_{x\ge 0}(x+\sum_{i=l}^r[a_i>x])=r-l+1+\min_{x\ge 0}(x-\sum_{i=l}^r[a_i\le x])=r-l+1-\max_{x\ge 0}(\sum_{i=l}^r[a_i\le x]-x)\)。所以我們只需要最小化 \(r-l+1-\max_{x\ge 0}(\sum_{i=l}^r[a_i\le x]-x)\),發現這個東西長得很像擴展 Hall 定理:
- 對于一個有 \(n\) 個左部點的二分圖,他的最大匹配是 \(n-\max(|S|-|N(S)|)\)。
再看回要求的那個式子,我們可以按照下面這種方式構造一張二分圖:所有左部點是 \(\{a_i|l\le i \le r\}\),所有右部點是 \(\{1,2,3,...,n\}\),\(a_i\) 和 \(j\) 之間有邊當且僅當 \(j\le a_i\)。會發現上面那個式子的最優值肯定是取在 \(x\) 等于某個 \(a_i\) 的時候,所以在考慮 Hall 定理的時候只需要考慮那些 \(S=\{a_i|a_i\le x\},N(S)=\{1,2,3,...,x\}\) 的情況,那么容易發現此時 \(r-l+1-\max_{x\ge 0}(\sum_{i=l}^r[a_i\le x]-x)\) 剛剛好就是這張二分圖的最大匹配。
因為這張二分圖的性質很好,我們有一個很簡單的貪心求最大匹配的方法:按任意順序加入左部點,加入到 \(a_i\) 的時候貪心地把最大的還沒匹配過的 \(x\le a_i\) 和 \(a_i\) 匹配。
觀察這個過程,容易發現這個過程并不會使得已經匹配過的點失配,那么如果可以離線的話,我們可以統一處理右端點為 \(r\) 的詢問,按順序加入 \(a_r,a_{r-1},a_{r-2},...a_1\),然后對于一個詢問 \([l,r]\) 就是看最終匹配的左部點里有多少個數的下標在 \([l,r]\) 范圍內。于是就得到了一個 \(O(n^2)\) 的離線做法。
如果想要優化這個做法,那么我們就需要知道當 \(r\to r+1\) 時,左部點的匹配狀態變成了什么樣。
因為此時 \(a_{r+1}\) 的優先級是最高的,所以我們需要強制 \(a_{r+1}=val\) 和右部的 \(val\) 點匹配,如果能直接加那最好,但是如果右部點 \(val\) 已經被匹配了,這樣會使得原先和右部點 \(val\) 匹配的左部點失配,于是我們就需要去找增廣路,但顯然這太麻煩了。
我們考慮用普通的 Hall 定理來判斷一個匹配的合法性,如果一個匹配的左部點的集合為 \(S\),那么這個匹配合法當且僅當 \(\forall x \in [1,n],(x-\sum_{a_i\in S} [x\le a_i])\ge 0\)。我們記 \(w_x = x-\sum_{a_i\in S} [x\le a_i]\),那么我們需要讓所有的 \(w\) 非負,當往匹配中加入一個 \(a_{r+1}\) 時,可能會使得某些 \(w_x<0\),我們找到其中最小的 \(x\) 滿足 \(w_x<0\),那么我們就是要在所有 \(a_i\in S,a_i\le x\) 中挑一個出來從匹配中刪掉,因為我們的貪心是按照下標從后往前加點的,所以我們需要把其中下標(注意不是值)最小的從匹配中刪掉。
用一棵線段樹維護 \(w_x\),用一棵線段樹維護還沒被刪掉的左部點,上面的過程都可以輕松維護,把維護左部點的線段樹可持久化就可以在線回答詢問了。
因為我們分成的 \(\log V\) 個子序列的點數之和是 \(O(n)\) 的,所以總復雜度是 \(O((n+Q)\log n)\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define LL long long
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2e5+5,inf=N;
int n,Q,t,st[20][N];
LL a[N];
int RMQ(int l,int r){
int k=__lg(r-l+1);
return max(st[k][l],st[k][r-(1<<k)+1]);
}
struct SegmentTree{
#define ls(p) t[p].ls
#define rs(p) t[p].rs
int tot=0;
struct node{
int ls,rs,cnt;
PII ming;
}t[N*40];
void build(){
t[0].cnt=t[0].ls=t[0].rs=0;
t[0].ming={inf,inf};
}
int New(int p){
t[++tot]=t[p];
return tot;
}
void pushup(int p){
t[p].cnt=t[ls(p)].cnt+t[rs(p)].cnt;
t[p].ming=min(t[ls(p)].ming,t[rs(p)].ming);
}
int change(int p,int l,int r,int x,int val){
int q=New(p);
if(l==r){
t[q].ming={val,l};
t[q].cnt=(val!=inf);
return q;
}
int mid=(l+r)>>1;
if(x<=mid) t[q].ls=change(ls(q),l,mid,x,val);
else t[q].rs=change(rs(q),mid+1,r,x,val);
pushup(q);
return q;
}
PII find(int p,int l,int r,int R){
if(l==r) return t[p].ming;
int mid=(l+r)>>1;
if(t[ls(p)].ming.fi<=R) return find(ls(p),l,mid,R);
else return find(rs(p),mid+1,r,R);
}
int ask(int p,int l,int r,int L,int R){
if(L<=l&&r<=R) return t[p].cnt;
int mid=(l+r)>>1,sum=0;
if(L<=mid) sum+=ask(ls(p),l,mid,L,R);
if(R>mid) sum+=ask(rs(p),mid+1,r,L,R);
return sum;
}
}Seg;
struct SegmentTree2{
struct node{
int l,r,add;
PII ming;
void tag(int d){
ming.fi+=d,add+=d;
}
}t[N<<2];
void pushup(int p){t[p].ming=min(t[p<<1].ming,t[p<<1|1].ming);}
void spread(int p){
if(t[p].add){
t[p<<1].tag(t[p].add);
t[p<<1|1].tag(t[p].add);
t[p].add=0;
}
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r,t[p].add=0;
if(l==r){
t[p].ming={l,l};
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid),build(p<<1|1,mid+1,r);
pushup(p);
}
void change(int p,int l,int r,int d){
if(l<=t[p].l&&t[p].r<=r){
t[p].tag(d);
return;
}
spread(p);
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) change(p<<1,l,r,d);
if(r>mid) change(p<<1|1,l,r,d);
pushup(p);
}
}Seg2;
struct WORK{
int rt[N];
int cnt=0,m=0,id[N],a[N],ID[N];
void insert(int i,LL val){
if(val==0) return;
if(val<=n) id[++cnt]=i,a[cnt]=val;
else ID[++m]=i;
}
void work(int K){
if(!cnt&&!m) return;
Seg2.build(1,1,n);
for(int i=1;i<=cnt;i++){
rt[i]=Seg.change(rt[i-1],1,n,id[i],a[i]);
Seg2.change(1,a[i],n,-1);
if(Seg2.t[1].ming.fi<0){
PII x=Seg.find(rt[i],1,n,Seg2.t[1].ming.se);
rt[i]=Seg.change(rt[i],1,n,x.se,inf);
Seg2.change(1,x.fi,n,1);
}
}
}
int query(int l,int r){
int L,R=upper_bound(id+1,id+cnt+1,r)-id-1,ans=0;
if(id[R]>=l) ans+=Seg.ask(rt[R],1,n,l,r);
L=lower_bound(ID+1,ID+m+1,l)-ID,R=upper_bound(ID+1,ID+m+1,r)-ID-1;
return ans+R-L+1;
}
}T[65];
void Init(){
for(int t=1;t<=__lg(n);t++)
for(int i=1;i+(1<<t)-1<=n;i++)
st[t][i]=max(st[t-1][i],st[t-1][i+(1<<(t-1))]);
for(int i=1;i<=n;i++) T[__lg(a[i])].insert(i,a[i]-(1ll<<__lg(a[i])));
Seg.build();
for(int i=0;i<60;i++) T[i].work(i);
}
signed main(){
freopen("repair.in","r",stdin);
freopen("repair.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>Q>>t;
for(int i=1;i<=n;i++) cin>>a[i],st[0][i]=__lg(a[i]);
Init();
LL lstans=0;
while(Q--){
LL l,r; cin>>l>>r;
if(t==2) l^=lstans,r^=lstans;
if(l>r) swap(l,r);
int k=RMQ(l,r);
printf("%lld\n",(lstans=r-l+1+(1ll<<k)+T[k].query(l,r)));
}
return 0;
}
C.人員調度 2
題意
有一張有 \(n\) 個左部點和 \(n\) 個右部點的二分圖,左部點 \(i\) 和右部點 \(j\) 之間有一條權值為 \(a_i + b_j + a_i \oplus b_j\) 的邊。
同時這張圖還有 \(m\) 條特殊邊,一條特殊邊 \((x,y,w)\) 表示左部點 \(x\) 和右部點 \(y\) 之間的邊的邊權在原來的基礎上再加 \(w\)。
給定一個 \(K\),對于每個 \(k\in [1,K]\),求這張二分圖大小為 \(k\) 的匹配中邊權和最大的匹配,輸出這個匹配的邊權和即可。
數據范圍: \(1\le n\le 10^5,0\le m \le 5\times 10^5,1\le K \le \min(300,n),0\le a_i,b_i < 2^{12},0\le w \le 10^5\) 保證不存在兩條特殊邊的 \(x,y\) 均相同。
時限: \(5s\)。
Day7 模擬賽
A.序列變換
題意
給一個長度為 \(n\) 下標從 \(1\) 開始的序列 \(a\),可以進行下列操作若干次:
- 選擇一個區間 \([l,r]\),對于所有 \(i\in N,x\in \{0,1\},l+3i+x\le r\) 將 \(a_{l+3i+x}\) 加上 \((-1)^x\)。
問最少需要操作幾次可以把 \(a\) 變成全 \(0\),無解輸出 \(-1\)。
多測。
數據范圍:\(T=30,n\le 3\times 10^4,|a_i|\le 10^{10}\)。
題解
神秘貪心題,完全不會做。
不妨設那些 \(i<1\) 或者 \(i>n\) 的 \(a_i\) 都是 \(0\),求出一個長度為 \(n+2\) 的序列 \(b\) 滿足 \(b_i=a_i+a_{i-1}+a_{i-2}\)。
那么一次操作其實只有兩種情況:
- \(l \equiv r \pmod 3\)(就是最后剩一個 \(+1\)):相當于是把 \(b_l+1,b_{r+1}+1,b_{r+2}+1\)。
- \(l \equiv r+1 \pmod 3\)(就是區間中 \(+1\) 和 \(-1\) 的數量相等)(\(l \equiv r-1 \pmod 3\) 的情況是等價的):相當于是把 \(b_l+1,b_{r+1}-1\)。
并且不難發現 1. 中的 \(l,r+1,r+2\) 模 \(3\) 兩兩不同余,2. 中的 \(l,r+1\) 模 \(3\) 同余。
目標就是把 \(b\) 全變成 \(0\)。
顯然操作 1 一定會讓 \(\sum b_i\) 加 \(3\),操作 2 不影響 \(\sum b_i\),因此操作 1 的操作次數已經確定了。并且如果 \(\sum b_i\) 不是 \(3\) 的倍數或者他 \(>0\) 就無解。
不妨先假設沒有操作 2,此時有一個貪心做法。
從后往前考慮每個 \(i\),如果有 \(b_i,b_{i-1}<0\),在上面執行一次操作 1,但是此時我們不知道前面的 \(l\) 是哪個位置,不過我們可以知道 \(l\bmod 3\) 的值,所以我們先用一個變量存儲,之后再去用。
如果當前的 \(b_i<0\) 但是 \(b_{i-1}=0\) 或者使用次數沒有了,那么我們就從之前存的對應的變量中取出一些填到這個位置上。
現在加上操作 2。
會發現只有操作 1 的情況不能做有 \(b_i>0\) 的情況,但是有了操作 2 就可以做了,因為操作 \(2\) 可以把某個數 \(-1\)。
還是考慮貪心,從后往前考慮,假設當前考慮到 \(t\),且 \(b_i (i>t)\) 已經都是 \(0\) 了,分類討論:
(1) \(b_t=0\):不管,跳過。
(2) \(b_t>0\):用操作 2,此時我們還是不去管前面的 \(l\) 到底是哪個位置,因為我們知道 \(l \equiv t \pmod 3\) 所以仍然用一個臨時變量存下來,之后再用。
(3) \(b_t<0\):依次進行下列過程:
- 如果 \(b_{t-1}<0\),那么就一直用操作 1 直到操作次數用完了,或者 \(max(b_t,b_{t-1})=0\)。
- 如果 \(b_t\) 還是 \(<0\),我們先去用之前存下來的那些值填上去。
- 如果 \(b_t\) 仍然 \(<0\),那就沒辦法了,我們只能用操作 2 強行把 \(b_{t-1}\) 壓下去變成和 \(b_t\) 一樣,然后再用操作 1,顯然此時如果操作次數不夠了就無解了。
正確性的話感性理解一下就是對的。
\(O(Tn)\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define int long long
using namespace std;
const int N=3e4+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int T,n,a[N],b[N];
int calc(int x,int y){
if(x!=0&&y!=0) return 0;
if(x!=1&&y!=1) return 1;
if(x!=2&&y!=2) return 2;
}
signed main(){
freopen("trans.in","r",stdin);
freopen("trans.out","w",stdout);
T=read(),n=read();
while(T--){
for(int i=1;i<=n;i++) a[i]=read();
a[n+1]=a[n+2]=0;
int sum=0;
for(int i=1;i<=n+2;i++) b[i]=a[i]+a[i-1]+((i==1)?0:a[i-2]),sum+=-b[i];
if(sum<0||sum%3!=0){
puts("-1");
continue;
}
int num[3]={0,0,0},cnt=sum/3,ans=0;
bool stater=true;
for(int i=n+2;i>=1;i--){
if(b[i]==0) continue;
if(b[i]>0) num[i%3]+=b[i],ans+=b[i];
else{
if(b[i-1]<0){
int deta=min(cnt,min(-b[i],-b[i-1]));
num[calc(i%3,(i-1)%3)]+=deta;
b[i]+=deta,b[i-1]+=deta;
cnt-=deta;
ans+=deta;
}
if(b[i]<0){
int deta=min(num[i%3],-b[i]);
num[i%3]-=deta;
b[i]+=deta;
}
if(b[i]<0){
if(!cnt||i==1){
stater=false;
break;
}
int deta=b[i-1]-b[i];
num[(i-1)%3]+=deta;
b[i-1]-=deta;
ans+=deta;
if(cnt<-b[i]){
stater=false;
break;
}
cnt-=-b[i];
num[calc(i%3,(i-1)%3)]+=-b[i];
ans+=-b[i];
b[i-1]+=-b[i],b[i]=0;
}
}
}
if(!stater) puts("-1");
else printf("%lld\n",ans);
}
return 0;
}
B.追憶
題意
給定一個數 \(n\) 和一個種子 \(seed\),由他生成一個 DAG,具體的生成過程如下:
- 對于所有 \(2\le i \le n\),在 \([1,i)\) 中隨機兩個數作為 \(a_i,b_i\),并由 \(i\) 向 \(a_i,b_i\) 連有向邊。
給你 \(n-1\) 個詢問,第 \(i\) 個詢問 \(x_i\) 滿足 \(1\le x_i \le i\),表示求 \(i+1\) 到 \(x_i\) 的最短路,到達不了答案就是 \(-1\)。
輸出 \(\oplus_{i=1}^{n-1} (ans_i+2)\times i\)。
數據范圍: \(1\le n \le 2\times 10^6\)。
題解
首先我們先證明一個點 \(x\) 可以到達的點的期望是 \(O(\sqrt{x})\) 的。
證明:\(<\sqrt{x}\) 的點有 \(O(\sqrt{x})\) 個,對于大于 \(O(\sqrt{x})\) 的點,如果我從 \(x\) 開始一直走,只走 \(>\sqrt{x}\) 的點,那么由圖的生成過程可知,每走一步點的編號期望 \(\times \frac{1}{2}\),因此期望只能走 \(O(\log_2 \frac{x}{\sqrt{x}})\) 步,每一步有兩種選擇,總共最多走不超過 \(O(2^{\log_2 \frac{x}{\sqrt{x}}})=O(\sqrt{x})\) 個點。
所以我們設一個閾值 \(B\),暴力預處理出 \(O(B^2)\) 個點對間的最短路,時間復雜度是 \(O(\sum_{i=1}^B \sqrt{i})=O(B^{\frac{3}{2}})\)。
對于詢問 \(dist(i+1,x_i)\),如果 \(i+1\le B\) 直接查表,否則從他開始 BFS,只走 \(> B\) 的點,走到 \(\le B\) 的點就直接查表之后返回。同理可以得到一次 BFS 的復雜度是 \(O(\frac{n}{B})\),因此回答詢問的總復雜度是 \(O(\frac{n^2}{B})\)。
平衡一下,取 \(B=n^{\frac{4}{5}}\approx 10^5\),時間復雜度是 \(O(n^{\frac{6}{5}})\)。
但是注意到你開不了 \(O(B^2)\) 的數組,所以可以把要用到的詢問離線下來之后統一處理。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define LL long long
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2e6+5,B=1e5;
int n,x[N],a[N],b[N],ans[N];
unsigned int seed;
unsigned shift(unsigned &a){
a^=a<<13;
a^=a>>7;
a^=a<<17;
return a;
}
void init(unsigned seed){
for(int i=2;i<=n;i++)
a[i]=shift(seed)%(i-1)+1,
b[i]=shift(seed)%(i-1)+1;
}
struct node{
int x,Dist,id;
};
vector<node> Que[B+5];
queue<int> Q;
int dist[B+5];
vector<int> vec;
void BFS(int s){
Q.push(s);
dist[s]=0;
while(Q.size()){
int u=Q.front(); Q.pop();
vec.emplace_back(u);
if(u==1) continue;
if(dist[a[u]]==n+5) dist[a[u]]=dist[u]+1,Q.push(a[u]);
if(dist[b[u]]==n+5) dist[b[u]]=dist[u]+1,Q.push(b[u]);
}
for(node que:Que[s]) ans[que.id]=min(ans[que.id],que.Dist+dist[que.x]);
for(int x:vec) dist[x]=n+5;
vec.clear();
}
void work(){
for(int i=1;i<=B;i++) dist[i]=n+5;
for(int i=1;i<=min(B,n);i++) BFS(i);
}
int BFS2(int s,int t){
queue<PII> Q;
Q.push({s,0});
while(Q.size()){
int u=Q.front().fi,Dist=Q.front().se; Q.pop();
int x=a[u],y=b[u];
if(x==t||y==t) return Dist+1;
if(x>B) Q.push({x,Dist+1});
else if(t<=B) Que[x].push_back({t,Dist+1,s-1});
if(y>B) Q.push({y,Dist+1});
else if(t<=B) Que[y].push_back({t,Dist+1,s-1});
}
return n+5;
}
signed main(){
freopen("recall.in","r",stdin);
freopen("recall.out","w",stdout);
scanf("%d%u",&n,&seed);
init(seed);
for(int i=1;i<n;i++) scanf("%d",&x[i]),ans[i]=n+5;
for(int i=1;i<n;i++){
if(i+1<=B) Que[i+1].push_back({x[i],0,i});
else ans[i]=BFS2(i+1,x[i]);
}
work();
LL res=0;
for(int i=1;i<n;i++){
if(ans[i]==n+5) ans[i]=-1;
res^=1ll*(ans[i]+2)*i;
}
printf("%lld\n",res);
return 0;
}
C.小方的疑惑
題意
有一個長度為 \(n\) 的非負整數序列 \(a\) 和一個長度為 \(n-1\) 的正整數序列 \(b\),其中 \(b_i\) 滿足 \(1\le b_i \le i\)。
可以執行以下操作若干次:
- 選擇一個 \(i\in [1,n)\),滿足 \(a_{b_i}>0\),將 \(a_{b_i}\) 減去 \(1\),將 \(a_{i+1}\) 加上 \(1\)。
求有多少種本質不同的序列 \(a\) 可以被生成,對 \(10^9+7\) 取模。
數據范圍:\(1\le n \le 8\times 10^3,0\le a_i \le 10^9\)。
Day8 模擬賽
A.平衡樹
題意
有一棵 \(n\) 個點的無根樹,每個點有點權 \(a_i\),其中有一些邊是關鍵邊,定義一條關鍵邊的不平衡度為:刪除這條邊之后,分成的兩棵子樹的點權和的差的絕對值。定義一棵樹的不平衡度為所有關鍵邊的不平衡度的最大值。
\(Q\) 次詢問,每次給出 \(k\) 條關鍵邊以及兩個非負整數 \(L,R\),一次操作定義為給一個點的點權 \(+1\),你至少操作 \(L\) 次,至多操作 \(R\) 次,問最終這棵樹的不平衡度最小是多少。
數據范圍:\(2\le n\le 3\times 10^5,1\le Q \le n,0\le a_i \le 10^6,0\le L,R \le 10^9,1\le k \le n-1,1\le \sum k \le n\)。
題解
首先不難證明如果有三條關鍵邊在同一條鏈上,那么中間的那條一定沒用,因為左右兩邊總有一條關鍵邊的不平衡度比他大。
也就是說如果我們把不包含關鍵邊的連通塊縮成一個點,那么會得到一棵只含關鍵邊的樹,此時有用的關鍵邊只有葉子連出去的邊。
再換句話說,有用的關鍵邊會形成一個菊花圖。
所以只要考慮菊花圖怎么做。
設此時所有點權之和是 \(S\),第 \(i\) 個葉子的點權為 \(s_i\),雖然可能會出現 \(2s_i>S\) 的情況,但容易證明這樣的 \(s_i\) 只有至多一個,且他無論如何不會成為不平衡度最大的,所以可以認為每條邊的不平衡度就是 \(S-2s_i\)。
顯然要這個式子取到最大值需要讓 \(s_i\) 盡可能小,所以我們先把 \(s_i\) 升序排序。
會發現我們每把最小值 \(+1\),不平衡度就會 \(-1\),但是當把最小值加到和次小值一樣時,之后一旦要改變最小值就得至少操作 \(\ge 2\) 次,不會減少不平衡度,因此最優策略就是把最小值加到和次小值一樣時就停手。
但是有了 \(L\) 的限制意味著我們在把最小值加到次小值之后可能還得繼續加,直到加滿 \(L\) 次。
不難 \(O(k)\) 地去模擬這個過程。
還有一個需要注意的點是,如果加到 \(L\) 次之后,場上剛剛好只有唯一的一個最小值,那么我們再花一次操作把這個最小值 \(+1\) 就能再讓不平衡度 \(-1\),此時就要花費 \(L+1\) 次操作了。
最后就是怎么搞出這個菊花圖,因為你不能直接像邊雙縮點那樣把整棵樹遍歷一遍,但是可以先用 樹狀數組+dfn序 來判斷出每條關鍵邊是否有用,如果有用意味著這條關鍵邊兩側的兩棵子樹一定有一棵不含任何關鍵邊,那么這棵子樹可以直接縮成一個點,且他就是這個菊花的一個葉子。
可能需要特判一下 \(k=1\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define int long long
using namespace std;
const int N=3e5+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,T,a[N],tot,head[N],to[N<<1],Next[N<<1];
struct Edge{
int u,v;
}E[N];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
int num,dfn[N],Size[N],fa[N],Sum[N];
void dfs(int u,int fa){
::fa[u]=fa;
dfn[u]=++num;
Size[u]=1;
Sum[u]=a[u];
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa) continue;
dfs(v,u);
Sum[u]+=Sum[v];
Size[u]+=Size[v];
}
}
struct BIT{
int c[N];
int lowbit(int x){return x&(-x);}
void add(int i,int x){for(;i<=n;i+=lowbit(i)) c[i]+=x;}
int ask(int i,int sum=0){
for(;i;i-=lowbit(i)) sum+=c[i];
return sum;
}
int query(int x,int y){
return ask(y)-ask(x-1);
}
}Bit;
int k,L,R,cnt,id[N],s[N];
void work(){
sort(s+1,s+cnt+1);
int lst=L,i;
for(i=1;i<cnt;i++){
if(i*(s[i+1]-s[i])<lst) lst-=i*(s[i+1]-s[i]);
else break;
}
if(i==1){
int deta=min(R,s[i+1]-s[i]);
printf("%lld\n",(Sum[1]+deta)-2*(s[i]+deta));
return;
}
int x=lst/i,y=lst%i;
s[i]+=x;
if(y==i-1&&L<R) printf("%lld\n",(Sum[1]+L+1)-2*(s[i]+1));
else printf("%lld\n",(Sum[1]+L)-2*s[i]);
}
signed main(){
freopen("balance.in","r",stdin);
freopen("balance.out","w",stdout);
n=read(),T=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
E[i]={u,v};
add(u,v),add(v,u);
}
dfs(1,0);
for(int i=1;i<n;i++) if(E[i].u==fa[E[i].v]) swap(E[i].u,E[i].v);
while(T--){
k=read(),L=read(),R=read();
for(int i=1;i<=k;i++){
id[i]=read();
Bit.add(dfn[E[id[i]].u],1);
}
if(k==1){
int x=Sum[E[id[1]].u],y=Sum[1]-x;
if(x>y) swap(x,y);
if(L<=y-x&&y-x<=R) puts("0");
else if(x+R<y) printf("%lld\n",y-x-R);
else if(x+L>y){
int z=y-x;
if((L-z)%2==0||L!=R) puts("0");
else puts("1");
}
}
else{
cnt=0;
for(int i=1;i<=k;i++){
int u=E[id[i]].u,num=Bit.query(dfn[u],dfn[u]+Size[u]-1);
if(k==1) s[++cnt]=min(Sum[u],Sum[1]-Sum[u]);
else if(num==1) s[++cnt]=Sum[u];
else if(num==k) s[++cnt]=Sum[1]-Sum[u];
}
work();
}
for(int i=1;i<=k;i++) Bit.add(dfn[E[id[i]].u],-1);
}
return 0;
}
B.上升樹
題意
有一棵 \(n\) 個點的樹,點有點權,一條路徑的權值定義為其上面的點按順序構成的序列的 \(LIS\)。
詢問刪除一個點后剩下的森林的所有路徑的權值的最大值最小是多少,你只需要回答這個最小值而不需要輸出具體刪除哪個點。
數據范圍:\(1\le n \le 10^5,1\le a_i \le n\)。
題解
首先指定根的情況下,求每個子樹內的最大 \(LIS\) 是個經典問題,有多種解法,如線段樹合并,長鏈剖分,dsu on tree 等等,選擇你喜歡的方式實現即可,這里不贅述。(不會的可以看 [THUSC 2021] 白蘭地廳的西瓜 或者 CF490F)。
下面默認用的是線段樹合并,復雜度 \(O(n\log n)\)。
解法一
首先考慮一個樹是鏈的情況的做法,我們先求出刪掉中點之后左右兩邊哪個 \(LIS\) 大,那么顯然要使 \(LIS\) 更小就要去更大的那一邊刪。每次取中點的話就需要求 \(O(\log n)\) 次 \(LIS\),總復雜度 \(O(n\log^2 n)\)。
考慮把他拓展到樹上,我們先求出刪去根之后的全局最長 \(LIS\),計入答案。然后看一下最長的 \(LIS\) 在哪棵子樹中,那么同理要使 \(LIS\) 變得更小一定是去那棵子樹里面刪。我們每次像點分治那樣選取重心作為根,那么就需要做 \(O(\log n)\) 次,總復雜度 \(O(n\log^2 n)\)。
解法二
考慮優化解法一,會發現其實遞歸到子樹里面去刪點之后沒有必要把整棵樹都重新做一遍,比如此時的根是 \(rt\),他有三棵子樹 \(v_1,v_2,v_3\),最長 \(LIS\) 在 \(v_1\) 子樹中,現在要遞歸到以 \(v_1\) 子樹的重心 \(u\) 為根來求答案。
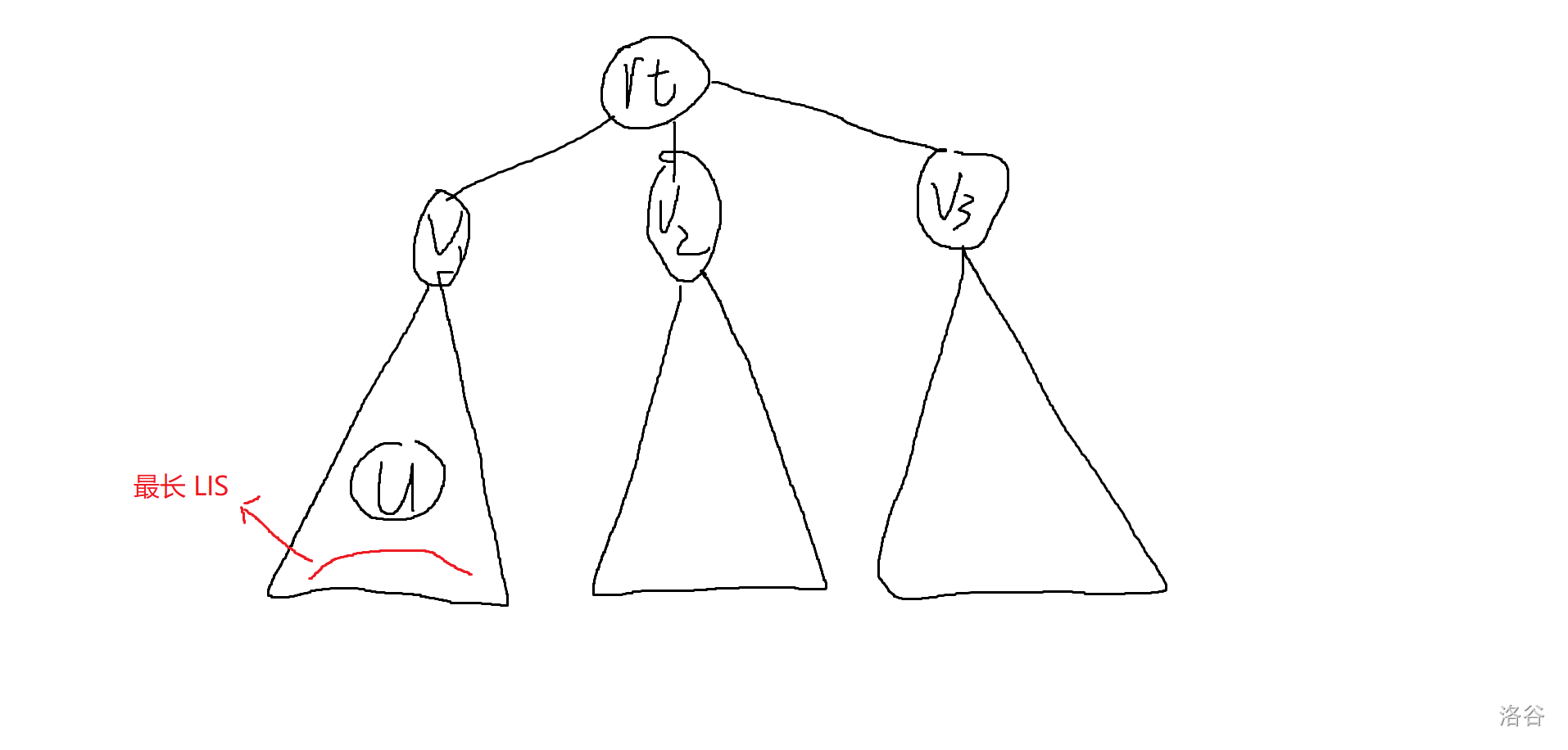
可能換根之后長這樣:
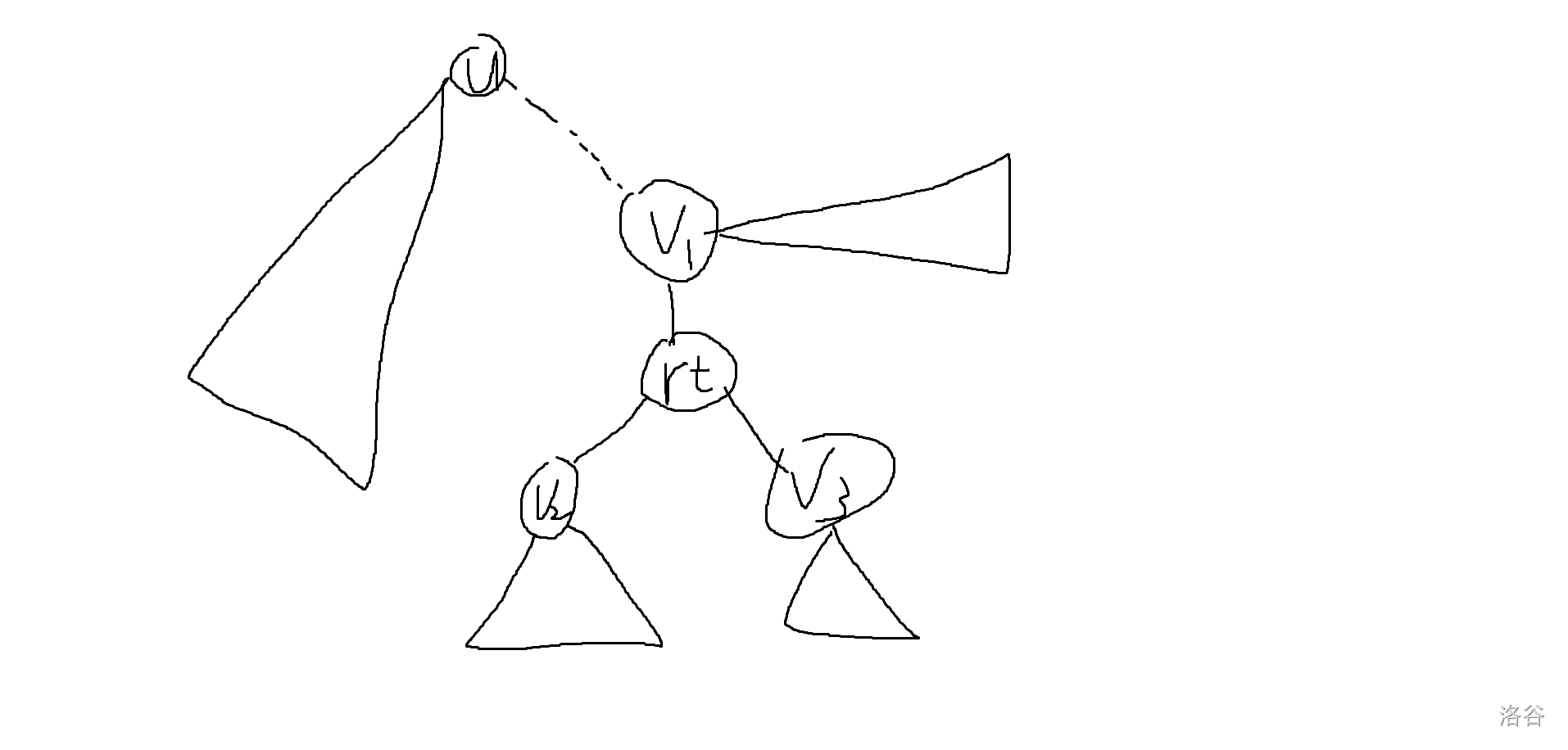
會發現其實我們沒有必要重新算一遍子樹 \(v2,v3\) 的答案,因為他們的形態并沒有改變,之后也不會再改變,同理 \(rt\) 這棵子樹之后的形態也不會變了,可以直接用 \(v2,v3\) 更新出他的信息。
所以我們在算以 \(u\) 為根的答案時,沒有必要再去做 \(rt\) 這棵子樹。
這樣每一次要重新做的樹的大小就是 \(n,\frac{n}{2},\frac{n}{4},...\),總復雜度就是 \(O(n\log n)\)。
解法三
如果我們能求出每個點子樹內和子樹外的最長 \(LIS\),那就可以快速求出刪掉每個點之后的答案。
但很可惜,子樹外的最長 \(LIS\) 并不好求。
換個角度考慮,我們剛才的思路是要使最長 LIS 變短就必須去他所在的子樹里面刪,但其實可以更進一步,容易證明我們要刪的一定是最長 \(LIS\) 所在鏈上面的點。
那么我們需要子樹外的最長 \(LIS\) 的那些點就只有這條鏈上的點的兒子或者父親,而這些信息只需要分別以這條鏈的兩端為根跑 dfs 就變成子樹內的信息了。
所以只需要會求子樹內的最長 \(LIS\) 即可。
因為筆者是懶蟲,所以只實現了最好實現的解法一。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define ls(p) t[p].ls
#define rs(p) t[p].rs
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1e5+5,inf=1e5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,a[N],tot,head[N],to[N<<1],Next[N<<1],Ans=N;
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
namespace Work{
PII operator + (const PII&x,const PII&y){return {max(x.fi,y.fi),max(x.se,y.se)};}
int rt[N],tot,ans[N];
struct node{
int ls,rs,f,g;
}t[N*20];
int New(){
++tot;
t[tot]={0,0,0,0};
return tot;
}
void pushup(int p){
t[p].f=max(t[ls(p)].f,t[rs(p)].f);
t[p].g=max(t[ls(p)].g,t[rs(p)].g);
}
void change(int &p,int L,int R,int x,int maxn1,int maxn2){
if(!p) p=New();
if(L==R){
t[p].f=max(t[p].f,maxn1);
t[p].g=max(t[p].g,maxn2);
return;
}
int mid=(L+R)>>1;
if(x<=mid) change(t[p].ls,L,mid,x,maxn1,maxn2);
else change(t[p].rs,mid+1,R,x,maxn1,maxn2);
pushup(p);
}
PII ask(int p,int L,int R,int l,int r){
if(!p||l>r) return {0,0};
if(l<=L&&R<=r) return {t[p].f,t[p].g};
int mid=(L+R)>>1;
if(r<=mid) return ask(t[p].ls,L,mid,l,r);
else if(l>mid) return ask(t[p].rs,mid+1,R,l,r);
else return ask(t[p].ls,L,mid,l,r)+ask(t[p].rs,mid+1,R,l,r);
}
int merge(int p,int q,int L,int R,int u){
if(!p||!q) return p+q;
if(L==R){
t[p].f=max(t[p].f,t[q].f);
t[p].g=max(t[p].g,t[q].g);
return p;
}
ans[u]=max({ans[u],t[ls(p)].f+t[rs(q)].g,t[ls(q)].f+t[rs(p)].g}); //統計經過 u 但是 u 不在 LIS 里的路徑的貢獻
int mid=(L+R)>>1;
t[p].ls=merge(t[p].ls,t[q].ls,L,mid,u);
t[p].rs=merge(t[p].rs,t[q].rs,mid+1,R,u);
pushup(p);
return p;
}
void dfs(int u,int fa){
ans[u]=1;
int maxn1=1,maxn2=1;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa) continue;
dfs(v,u);
ans[u]=max(ans[u],ans[v]);
int Up=ask(rt[v],1,inf,1,a[u]-1).fi,Down=ask(rt[v],1,inf,a[u]+1,inf).se;
maxn1=max(maxn1,Up+1);
maxn2=max(maxn2,Down+1);
ans[u]=max(ans[u],ask(rt[u],1,inf,1,a[u]-1).fi+1+Down);
ans[u]=max(ans[u],Up+1+ask(rt[u],1,inf,a[u]+1,inf).se);
rt[u]=merge(rt[u],rt[v],1,inf,u);
}
change(rt[u],1,inf,a[u],maxn1,maxn2);
ans[u]=max({ans[u],t[rt[u]].f,t[rt[u]].g});
}
int Main(int root){
tot=0;
for(int i=1;i<=n;i++) rt[i]=ans[i]=0;
dfs(root,0);
int son=0;
for(int i=head[root];i;i=Next[i]){
int v=to[i];
if(ans[v]>ans[son]) son=v;
}
Ans=min(Ans,ans[son]);
return son;
}
};
int Size[N],rt,num,maxn[N];
bool vis[N];
void dfs(int u,int fa,bool op){
Size[u]=1,maxn[u]=0;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa||vis[v]) continue;
dfs(v,u,op);
Size[u]+=Size[v];
if(op) maxn[u]=max(maxn[u],Size[v]);
}
if(op){
maxn[u]=max(maxn[u],num-Size[u]);
if(maxn[u]<maxn[rt]) rt=u;
}
}
void solve(int t){
vis[t]=true;
int u=Work::Main(t);
if(vis[u]) return;
rt=0;
maxn[rt]=num=Size[u];
dfs(u,0,1);
dfs(u,0,0);
solve(rt);
}
signed main(){
freopen("lis.in","r",stdin);
freopen("lis.out","w",stdout);
n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v),add(v,u);
}
rt=0;
maxn[rt]=num=n;
dfs(1,0,1);
dfs(rt,0,0);
solve(rt);
printf("%d\n",Ans);
return 0;
}
C.并行程序
題意
有 \(n\) 個程序,所有程序共享一個全局整形變量 \(x\),同時第 \(i\) 個程序有一個專屬的私有計數器 \(y\),第 \(i\) 個程序由 \(l_i\) 個指令組成,每個指令都屬于以下四種類型:
W:將全局變量 \(x\) 的值寫入私有計數器 \(y\),即令 \(x\to y\)。Z:將私有計數器 \(y\) 的值寫入全局變量 \(x\),即令 \(x\gets y\)。+ c:表示將私有計數器 \(y\) 的值加上正常數 \(c\)。- c:表示將私有計數器 \(y\) 的值減去正常數 \(c\)。
初始時 \(x\) 和所有 \(y\) 都是 \(0\)。
你需要指定某種順序來執行這 \(n\) 個程序,具體的,記某一時刻第 \(i\) 個程序已經執行了 \(a_i\) 個指令,那么下一個時刻你需要選擇一個 \(i\in [1,n],a_i<l_i\),并執行這個程序的第 \(a_i+1\) 個指令。
問所有程序都執行完畢后,\(x\) 的值最小可能是多少。
多測。
數據范圍:\(1\le T,n,l_i \le 10^6,1\le c \le 10^9\),一個測試點中所有數據的 \(\sum l_i\) 之和不超過 \(10^6\)。
時限: \(9s\)。
題解
Day10 模擬賽
什么網格專場。
A.這是第一題
題意
一張 \(n\times m\) 的網格,下標從 \(1\) 開始,列之間是循環的,即 \(m+1\) 列其實是第 \(1\) 列,\(-1\) 列其實是第 \(m\) 列。(行是不循環的)
有些格子上有障礙(#),有些格子上有硬幣 (B),其余格子都是空地(.),Alice 和 Bob 在上面博弈,輪流操作,Alice 先手,操作的人需要選擇一個硬幣,假設他的坐標是 \((i,j)\),并把這個硬幣移到 \((i+1,j),(i,j+1),(i,j-1)\) 三個位置中的一個。需要保證每個硬幣不能重復經過一個格子兩次(不同的硬幣之間互不影響,允許硬幣重疊)。不能操作的人輸。
請求出獲勝者是誰。
數據范圍:\(1\le n,m\le 10^3\)。
題解
題意等價于求出每個棋子的 SG 值。
設 \(F(x,y,[l,r])\) 表示目前在位置 \((x,y)\),第 \(x\) 行的 \([l,r]\) 已經被走過了(如果 \(l>r\) 意味著走過的是 \([l,m]\cup [1,r]\)),此時的 SG 值。容易發現除了 \(l=r\) 的情況必然有 \(y=l\)(即只能往左走) 或者 \(y=r\)(即只能往右走)。那么 \(SG(x,y)\) 就等于 \(mex(SG(x+1,y),F(x,y-1,[y-1,y]),F(x,y+1,[y,y+1]))\)。
以 \(y=l<r\) 為例。
雖然狀態數還是有 \(O(nm^2)\),但是會發現 SG 值的值域很小,只有 \(0,1,2,3\) 四種情況,且 \(F(x,y,[y,r])\) 的值在知道 \(F(x,m,[m,r])\) 后就可以推出來了,那么可以設 \(G(x,y,c)\) 表示當 \(F(x,m,[m,r])=c\) 時 \(F(x,y,[y,r])\) 的值,\(G\) 可以 \(O(m)\) 遞推。對于不合法情況 SG 值就設為 \(-1\)。
現在還需要知道每個 \(r\) 對應的 \(F(x,m,[m,r])\)。同樣的,\(F(x,m,[m,r])\) 在知道 \(F(x,t,[t,r]),t\ge r\) 的值之后就可以推出來了。所以設 \(H(x,t,c)\) 表示當 \(F(x,t,[t,r])=c\) 時 \(F(x,m,[m,r])\) 的值,\(H\) 也可以 \(O(m)\) 遞推。那么 \(F(x,m,[m,r])\) 就等于 \(H(x,r,-1)\)。
復雜度 \(O(nm)\)。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define eb emplace_back
#define LEFT 1
#define RIGHT 0
using namespace std;
const int N=1e3+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
int n,m,SG[N][N],f[N][N][3];;
char c[N][N];
bool stater[N];
bool flag[4];
bool check(int i,int j){ return c[i][j]!='#'; }
int mex(vector<int> vec){
flag[0]=flag[1]=flag[2]=flag[3]=0;
for(int x:vec) if(x<=3) flag[x]=true;
int ans=0;
while(flag[ans]) ans++;
return ans;
}
int mex2(int x,int y){
if(x!=0&&y!=0) return 0;
if(x!=1&&y!=1) return 1;
return 2;
}
int dfs(int i,int j,int op){
if(f[i][j][op]!=-1) return f[i][j][op];
vector<int> vec;
if(i<n&&check(i+1,j)) vec.eb(SG[i+1][j]);
if(op==2){
if(check(i,(j-1+m)%m)) vec.eb(dfs(i,(j-1+m)%m,LEFT));
if(check(i,(j+1)%m)) vec.eb(dfs(i,(j+1)%m,RIGHT));
}
else if(op==LEFT){
if(check(i,(j-1+m)%m)) vec.eb(dfs(i,(j-1+m)%m,LEFT));
}
else{
if(check(i,(j+1)%m)) vec.eb(dfs(i,(j+1)%m,RIGHT));
}
return f[i][j][op]=mex(vec);
}
int G[N][4],F[N],H[N][4],Left[N],Right[N];
void work(int x,int f[]){
for(int y=0;y<m;y++){
for(int c=0;c<=3;c++){
if(y==0) G[y][c]=mex2(c,SG[x+1][y]);
else if(y==m-1) G[y][c]=c;
else G[y][c]=mex2(G[y-1][c],SG[x+1][y]);
}
}
for(int t=m-1;t>=0;t--){
for(int c=0;c<=3;c++){
if(t==m-1) H[t][c]=c;
else H[t][c]=H[t+1][mex2(c,SG[x+1][t+1])];
}
}
for(int r=0;r<m;r++) F[r]=H[r][3];
for(int y=0;y<m;y++) f[y]=G[(y-1+m)%m][F[y]];
}
signed main(){
freopen("first.in","r",stdin);
freopen("first.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=0;j<m;j++){
cin>>c[i][j];
if(c[i][j]=='#') stater[i]=true;
f[i][j][0]=f[i][j][1]=f[i][j][2]=-1;
}
}
for(int j=0;j<m;j++) SG[n+1][j]=4;
int res=0;
for(int x=n;x>=1;x--){
if(m==1){
if(c[x][0]=='#') SG[x][0]=4;
else SG[x][0]=(SG[x+1][0]==0)?1:0;
}
else if(stater[x]){
for(int y=0;y<m;y++){
if(c[x][y]=='#') SG[x][y]=4;
else SG[x][y]=dfs(x,y,2);
}
}
else{
work(x,Left);
reverse(c[x],c[x]+m);
for(int i=0;i<m-1-i;i++) swap(SG[x+1][i],SG[x+1][m-1-i]);
work(x,Right);
reverse(Right,Right+m);
reverse(c[x],c[x]+m);
for(int i=0;i<m-1-i;i++) swap(SG[x+1][i],SG[x+1][m-1-i]);
for(int y=0;y<m;y++){
vector<int> vec;
vec.eb(Left[y]),vec.eb(Right[y]),vec.eb(SG[x+1][y]);
SG[x][y]=mex(vec);
}
}
for(int y=0;y<m;y++) if(c[x][y]=='B') res^=SG[x][y];
}
puts(res?"Alice":"Bob");
return 0;
}
B.這是第二題
題意
有一個 \(2n\times 2m\) 的網格,下標從 \(0\) 開始,初始網格的 \((i,j)\) 格子上的數是 \(2mi+j+1\)。并對網格按照 \(2\times 2\) 為單位進行交替黑白染色。
你需要維護下面五個操作:
- \(\forall 0\le j < m\),交換 \(2j,2j+1\) 這兩列。
- \(\forall 0\le j<m-1\),交換 \(2j+1,2j+2\) 這兩列。
- \(\forall 0\le i < n\),交換 \(2i,2i+1\) 這兩行。
- \(\forall 0\le i<n-1\),交換 \(2i+1,2i+2\) 這兩行。
- 對于每一個黑色 \(2\times 2\) 正方形,把里面的數按照順時針旋轉;對于每一個白色 \(2\times 2\) 正方形,把里面的數按照逆時針旋轉。
現在給出一個長度為 \(Q\) 的操作序列,請輸出最終的網格。
數據范圍:\(1\le Q,nm\le 10^6\)。
題解
會發現 \(2,4\) 操作非常不友好,因為他們并不會操作到第一列(行)和最后一列(行)。
我們可以把原圖不斷地鏡像對稱,鋪滿整個平面,但注意此時依舊是交替進行黑白染色,不是復制原圖的顏色,比如當 \(n=2,m=2\) 時鏡像三次就如下圖所示(黑框中的數就是染黑的):
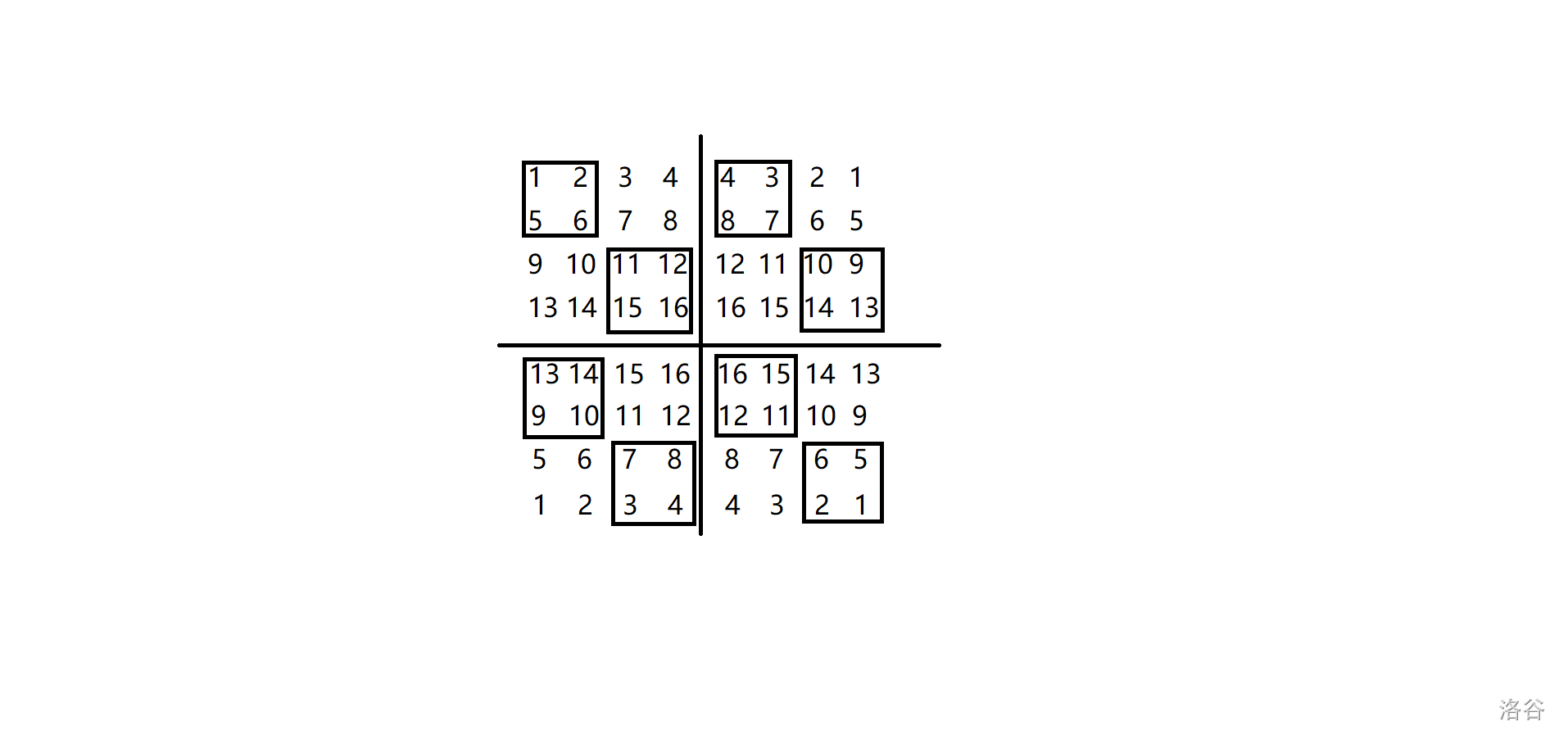
會發現此時相鄰邊界上的數是一模一樣的,也就是說此時進行 \(2\) 操作可以認為是交換所有的 \(2j+1,2j+2\) 列(\(4\) 操作同理)。
并且不難驗證此時 \(1,3,5\) 操作操作完同樣可保證相鄰邊界上的數一樣
所以此時一個點最終橫縱坐標的平移量只跟他初始橫縱坐標的奇偶性和顏色決定,因此只需要模擬 \(2\times 2\times 2\) 個點的軌跡即可。
最后再把每個點的坐標鏡像回去就可以了。
code
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1e6+5;
inline int read(){
int w=1,s=0;
char c=getchar();
for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
return w*s;
}
PII operator + (const PII&x,const PII&y){ return {x.fi+y.fi,x.se+y.se}; }
int n,m,Q,x[N];
bool staterA=true,staterC=true;
int Val(int i,int j){return 2*m*i+j+1;}
PII deta[2][2][2];
int calc(int val){
if(val>=0) return val/2;
else return (val-1)/2;
}
int calc1(int y){return (y%2==0)?1:(-1);}
int calc2(int y){return (y%2==0)?(-1):1;}
int calc3(int x){return (x%2==0)?1:(-1);}
int calc4(int x){return (x%2==0)?(-1):1;}
int get(int i,int j,int k,int x,int y){
bool flag=0;
if(calc(x+i)%2!=0) flag^=1;
if(calc(y+j)%2!=0) flag^=1;
return k^flag;
}
PII calc5(int x,int y,int c){
x=abs(x%2),y=abs(y%2);
if(c==0){ //Black
if(x==0&&y==0) return {0,1};
if(x==0&&y==1) return {1,0};
if(x==1&&y==1) return {0,-1};
if(x==1&&y==0) return {-1,0};
}
else{ //White
if(x==0&&y==0) return {1,0};
if(x==0&&y==1) return {0,-1};
if(x==1&&y==1) return {-1,0};
if(x==1&&y==0) return {0,1};
}
}
vector<vector<int> > a;
int Get(int x,int n){
int cnt=1+x/(2*n);
x=x%(2*n);
if(cnt&1) return x;
else return 2*n-1-x;
}
signed main(){
freopen("second.in","r",stdin);
freopen("second.out","w",stdout);
n=read(),m=read(),Q=read();
for(int i=0;i<=1;i++) for(int j=0;j<=1;j++) for(int k=0;k<=1;k++) deta[i][j][k]={0,0};
for(int _=1;_<=Q;_++){
x[_]=read();
for(int i=0;i<=1;i++){
for(int j=0;j<=1;j++){
for(int k=0;k<=1;k++){
if(x[_]==1) deta[i][j][k].se+=calc1(j+deta[i][j][k].se);
if(x[_]==2) deta[i][j][k].se+=calc2(j+deta[i][j][k].se);
if(x[_]==3) deta[i][j][k].fi+=calc3(i+deta[i][j][k].fi);
if(x[_]==4) deta[i][j][k].fi+=calc4(i+deta[i][j][k].fi);
if(x[_]==5) deta[i][j][k]=deta[i][j][k]+calc5(i+deta[i][j][k].fi,j+deta[i][j][k].se,get(i,j,k,deta[i][j][k].fi,deta[i][j][k].se));
}
}
}
}
a.resize(2*n);
for(int i=0;i<2*n;i++) a[i].resize(2*m);
for(int i=0;i<2*n;i++){
for(int j=0;j<2*m;j++){
int x=i+deta[i&1][j&1][(i/2%2+j/2%2)%2].fi,y=j+deta[i&1][j&1][(i/2%2+j/2%2)%2].se;
if(x<0) x=-x-1;
if(y<0) y=-y-1;
x=Get(x,n),y=Get(y,m);
a[x][y]=Val(i,j);
}
}
for(int i=0;i<2*n;i++){
for(int j=0;j<2*m;j++){
printf("%d ",a[i][j]);
}
puts("");
}
return 0;
}
C.這是第三題
題意
有一個大小為 \(n\times m\) 的網格,初始有一些格子上有棋子,現在你需要在一些空格子上再放上一些棋子,使得存在唯一的一種匹配棋子的方式。你需要輸出最少新放的棋子數,或者報告無解。
一種匹配棋子的方式合法當且僅當每個棋子都在一組匹配中,且一組匹配中的兩個棋子在同一行或者同一列。
數據范圍:\(1\le n,m\le 10^3\)。
Day11 模擬賽
A.硬幣
題意
這是一道交互題。
有 \(n\) 堆硬幣,下標從 \(0\) 開始,第 \(i\) 堆硬幣的硬幣數量是 \(a_i\),有且僅有一堆硬幣全是假幣,其余都是真幣。一枚真幣的重量是 \(5\),一枚假幣的重量是 \(6\)。
每次你可以向交互庫詢問一個長度為 \(n\) 的數組 \(p\) 滿足 \(0\le p_i \le a_i\) 表示從第 \(i\) 堆硬幣中取出 \(p_i\) 個硬幣,最后交互庫會返回從這 \(n\) 堆硬幣中取出的所有硬幣的重量和。
你需要求出假硬幣是哪一個堆,并最小化詢問次數。
數據范圍: \(1\le n\le 10^6,1\le a_i\le 10^9\)。
題解
首先詢問返回的結果等價于取出的硬幣中假幣的數量,換句話說,如果取出的假幣的數量是 \(x\),那么假幣只能在那些 \(p_i=x\) 的堆中。
所以每一次詢問相當于把硬幣分成若干個集合,然后可以知道假幣具體在哪個集合中。
所以詢問策略就是一棵樹,有 \(n\) 個葉子,每個葉子代表一堆硬幣,非葉結點的 \(p\) 值需要小于等于子樹中所有葉子的 \(a\) 值。
容易發現如果一個集合中的數在排序后滿足 \(a_i\ge i-1\),那么可以把他們的 \(p_i\) 依次設為 \(0,1,2,...\),因為 \(p_i\) 互不相同所以可以直接確定假幣在哪一堆。否則無法一次詢問直接找出假幣。因此上面劃分集合的時候需要滿足這個限制。
所以可以得到答案的下界:\(\max_{x\ge 2}(\log_x (\sum_{y<x} cnt_y))\),其中 \(cnt_y\) 表示 \(a_i=y\) 的數量。
證明:顯然對于每一個 \(x\),原問題比 \(\sum_{y<x} cnt_y\) 個 \(x-1\) 要難,而這個新問題的最優策略顯然是 \(x\) 叉樹(即每次選出來 \(x\) 個數放到一個集合,\(p_i\) 分別分配 \(0,1,2,...,x-1\)),此時答案是 \(\log_x(\sum_{y<x} cnt_y)\)。
要想達到這個下界可以直接貪心,從下往上構造這棵樹,每次把點排序后從前往后考慮,如果他能放到當前的某個集合中就放,否則新開一個集合。最后把得到的每個集合當做上一層的節點,權值就設為集合中點權的最小值即可。
復雜度隨便實現基本都是對的。
code
#include "coins.h"
#include<bits/stdc++.h>
#define fi first
#define se second
#define LL long long
#define PIV pair<int,vector<int> >
#define PII pair<int,int>
#define Debug puts("-----------------------------")
using namespace std;
const int N=1e6+5;
int n,a[N];
int solve(vector<PIV> vec){
if(vec.size()==1) return 0;
vector<int> b(vec.size());
for(int i=0;i<vec.size();i++) b[i]=i;
sort(b.begin(),b.end(),[&](int x,int y){return vec[x].fi<vec[y].fi;});
vector<PIV> node;
vector<vector<int> > ID;
int num=0;
set<PII> S;
for(int _=0;_<vec.size();_++){
PIV u=vec[b[_]];
int pos=0;
if(S.size()&&u.fi>=(*S.begin()).fi) pos=(*S.begin()).se,S.erase(S.begin());
else ++num,pos=num-1,node.resize(num),ID.resize(num),node[num-1].fi=INT_MAX;
node[pos].fi=min(node[pos].fi,u.fi);
ID[pos].emplace_back(b[_]);
S.insert({ID[pos].size(),pos});
for(int x:u.se) node[pos].se.emplace_back(x);
}
int number=solve(node);
vector<int> p(n);
LL sum=0;
for(int i=0;i<ID[number].size();i++){
int x=ID[number][i];
for(int y:vec[x].se) sum+=i,p[y]=i;
}
LL deta=weigh(p)-5*sum;
return ID[number][deta];
}
int solve(vector<int> A) {
n=A.size();
vector<pair<int,vector<int> > > all(n);
for(int i=0;i<n;i++) a[i]=A[i],all[i]={a[i],{i}};
return solve(all);
}
B.厵神
題意
有一個大小為 \(n\times m\) 的網格 \(a\),初始每個 \(a_{i,j}=1\)。
每一秒結束時,\(a_{i,j}\) 都會變成 \(a_{i,j-1}+a_{i,j+1}+a_{i-1,j}+a_{i+1,j}\)(越界的話就當做 \(0\))。
特殊的,在第 \(t\) 秒結束時,\(a_{x,y}\) 會變成 \(0\)。
現在請你求出在第 \(t'\) 秒結束時,\(a_{x',y'}\) 對 \(1004535809\) 取模的值。
數據范圍:\(2\le n\le 10^9,1\le m \le 10^9,1\le x,x' \le n,1\le y,y' \le m,1\le t \le 2\times 10^9,1\le t' \le 10^5\)。
C.區間壓縮
題意
太長了,直接上圖。

數據范圍: \(1\le n,q \le 5\times 10^5,1\le l_i\le r_i \le 10^6,1\le x_i\le y_i \le 10^6\)。


 浙公網安備 33010602011771號
浙公網安備 33010602011771號