求任意多邊形的面積（轉）

原文地址：http://blog.csdn.net/sun_shine_/article/details/18799739

給定多邊形的頂點坐標（有序），讓你來求這個多邊形的面積，你會怎么做？
我們知道，任意多邊形都可以分割為N個三角形，所以，如果以這為突破點，那么我們第一步就是把給定的多邊形，分割為數個三角形，分別求面積，最后累加就可以了，把多邊形分割為三角形的方式多種多樣，在這里，我們按照如下圖的方法分割：

圖1

S點作為起始點（點1），a->e依次作為點2,3……。
一個三角形的面積是怎樣的呢？
根據線性代數的知識，我們有如下的三角形面積公式，稱之為有向面積(signed area)：

將這個行列式以第三列展開可以得到：

這就是以點1、2、3構成的三角形的有向面積（點如果是順時針給出，有向面積為負，逆時針給出，有向面積為正），那么繼續我們的工作，通過三角形的面積公式，來得到多邊形的面積公式：
對于圖1而言，多邊形的面積就是：
S(1->6)=S(1,2,3)+S(1,3,4)+S(1,4,5)+S(1,5,6)
這里我們不免有些疑問，第一，圖1所給出的是凸多邊形，那這種算法對于非凸多邊形是否同樣適用呢？比如下面這個最簡單的凸多邊形的圖形：

圖2

用剛才的劃分方法的話，就會出現一個詭異的問題，那就是有一個三角形出現在了圖形的外面，而另外一個又超出了多邊形的范圍（劃分為了Sab，Sbc兩個圖形），那么這樣再用剛才的公式求面積，結果還是正確的么？
S(1->4)=S(1,2,3)+S(1,3,4)
先公布結論，這個式子是正確的，等等，為什么？還記得剛才我提到了那個“有向面積”的概念么？忘了的話，請回頭看看加重了的字。
請注意從圖中看，Sab點為順時針排列，Sbc點為逆時針排列，面積從數值上就是從Sab這個超過范圍的大三角形中去掉Sbc這個小三角形，最后的結果神奇的就是多邊形Sabc的面積，那么這個結論能否推廣到任意多邊形呢？

圖3

在這里不做證明，下面給出的公式，就是任意多邊形的面積公式：

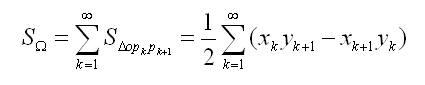
例題：

Input

輸入數據包含多個測試實例，每個測試實例占一行，每行的開始是一個整數n(3<=n<=100)，它表示多邊形的邊數（當然也是頂點數），然后是按照逆時針順序給出的n個頂點的坐標（x1, y1, x2, y2... xn, yn）,為了簡化問題，這里的所有坐標都用整數表示。 
輸入數據中所有的整數都在32位整數范圍內，n=0表示數據的結束，不做處理。 

 

Output

對于每個測試實例，請輸出對應的多邊形面積，結果精確到小數點后一位小數。 
每個實例的輸出占一行。 

 

Sample Input

3 0 0 1 0 0 1 4 1 0 0 1 -1 0 0 -1 0

 

Sample Output

0.5 2.0

 

 代碼：

#include<cstdio>
#include<cmath>

int main(){
     int n;
     int p[110][2];
     while(scanf("%d",&n)&& n){
          for(int i = 0; i < n; i ++)
          scanf("%d%d",&p[i][0],&p[i][1]);
          p[n][0] = p[0][0];
          p[n][1] = p[0][1];
          int s = 0;
          for(int i = 0; i < n; i ++){
               s += (p[i][0]*p[i+1][1] - p[i+1][0]*p[i][1]);
          }
          printf("%.1lf\n",s/2.0);
     }
return 0;
}

View Code

注意上面的公式是循環一周的，最后Xn*Y1-X1*Yn也要加進去 = =