【圖像處理筆記】小波變換
0 引言
1987年,小波被證明是多分辨率信號處理和分析的基礎。多分辨率理論融合并統一了來自不同學科的技術,包括來自信號處理的子帶編碼、來自數字語音識別的正交鏡像濾波及金字塔圖像處理。顧名思義,多分辨率理論涉及多個分辨率下的信號(或圖像)表示與分析。
曾經有人問我有關haar的東西,我沒答上來,耿耿于懷,所以我從傅里葉變換學到小波變換再到haar小波,驀然回首,才發現他當時問的是haar特征。但是,學都學了...ps:Haar-like特征是計算機視覺領域一種常用的特征描述算子,也稱為Haar特征,這是因為Haar-like是受到一維haar小波的啟示而發明的,所以稱為類Haar特征。
1 從傅里葉變換到小波變換
1.1 傅里葉變換
對于大多數信號而言, 傅立葉分析絕對是非常有用的,因為頻率分析在大多數情況下都非常重要。 那么為什么我們還需要研究短時傅里葉變換呢(STFT)?原因是因為傅立葉分析有一個非常嚴重的缺點, 在將信號從時間域變換到頻率域去的時候,把時間信息丟失了。 當我們在用傅立葉變化去分析一個具體信號的時候, 我們不知道哪個頻率是對應在哪個時間點出現的,在哪個時間點消失的。假設有兩個信號,這兩個信號都是由sin(t)和sin(5t)組成的,y1是先出現了sin(5t),再出現了sin(t),y2是先出現了sin(t),再出現了sin(5t)。
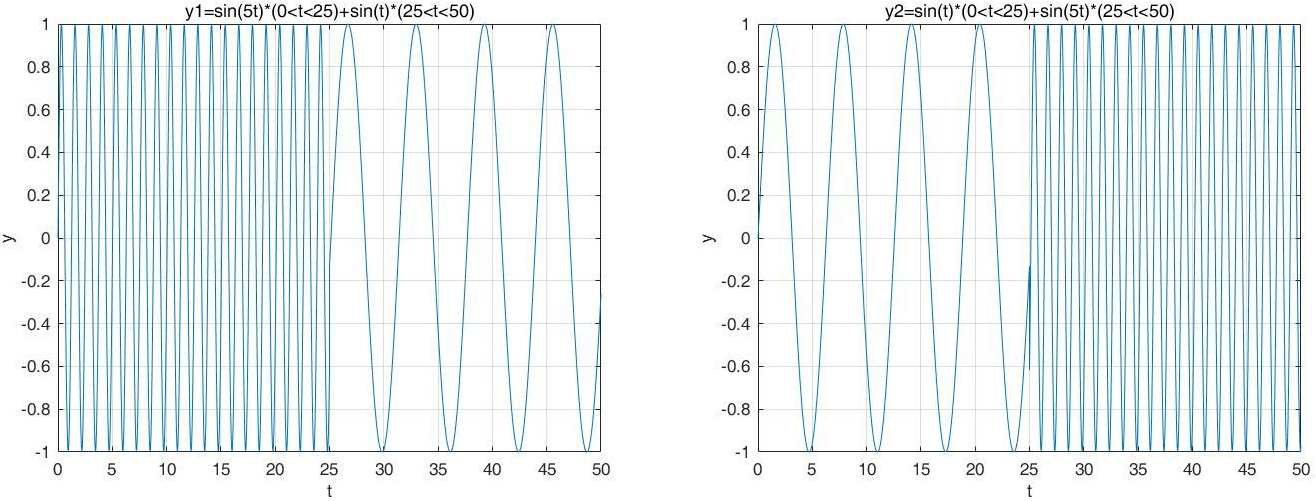
進行傅里葉變換后的頻譜為
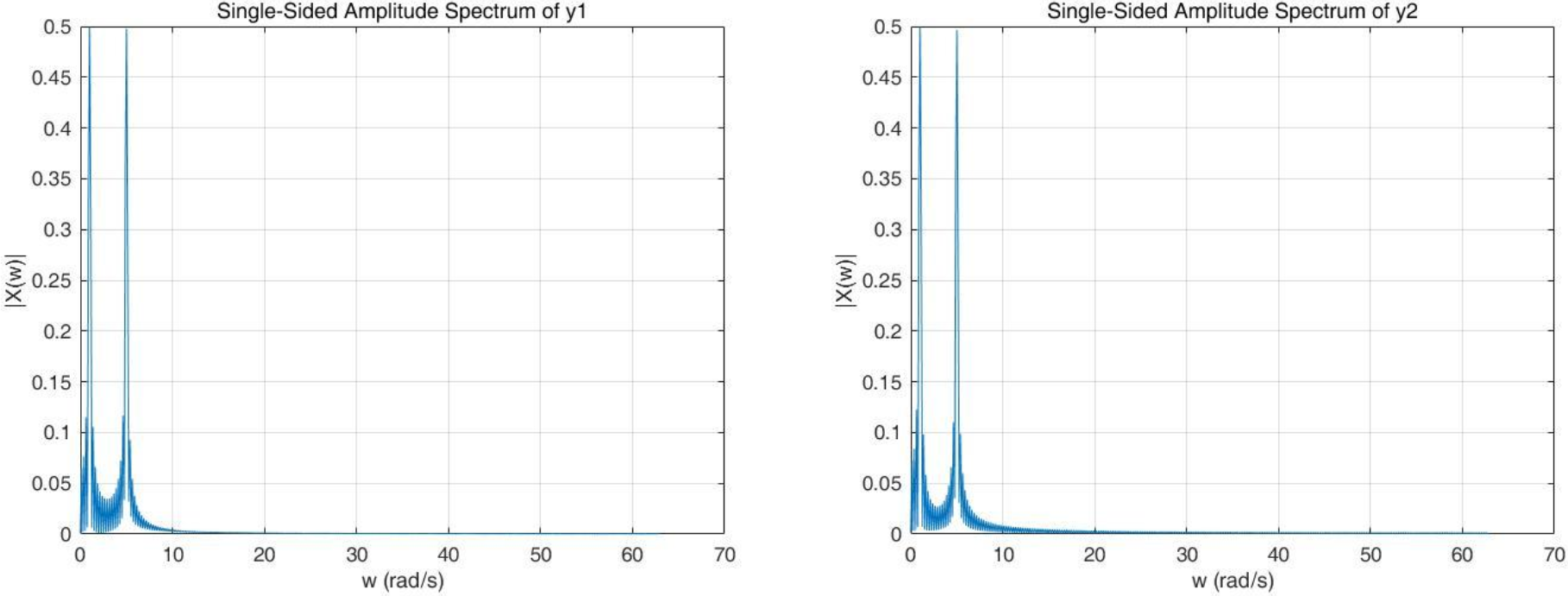
可以看出,變換后的結果是一模一樣的,都在w=1rad/s和w=5rad/s出現了峰值,這就可以說明FT的缺點了——FT只能提供頻域信息,而完全丟失了時域信息。不管某一頻率的信號出現的時間是早還是晚,FT都是將它一視同仁地乘上sin和cos(FT的變換基函數),然后在整個時間區間加和。因此,它不能提供某一頻率信號出現的時間。如果一個信號的頻率并不隨著時間變化, 那么我們稱它為平穩信號。 那么知道哪一個頻率的信號在哪一個時間點出現的就不那么重要了。可是如果現實生活中我們研究的大多數信號都是非平穩信號,他們都許多非常短暫變化的特性, 這些特點對于我們信號分析的特點,傅立葉分析并不適合去做這種分析,而短時傅里葉變換則可以。
1.2 短時傅里葉變換
我們將信號從中間截斷,左邊進行一次FT,右邊進行一次FT,便可以得到,在y1中(0, 25)的信號是5rad/s的頻率,(25, 50)的信號是5rad/s的頻率,y2恰好相反。這就是短時傅里葉變換的基本原理。截斷的方法在專業上將叫分窗——有一個窗子在信號上從左向右滑動,每次只能看到信號的一部分,相當于把整個時域過程分解成無數個等長的小過程,再傅里葉變換,就知道在哪個時間點上出現了什么頻率了。
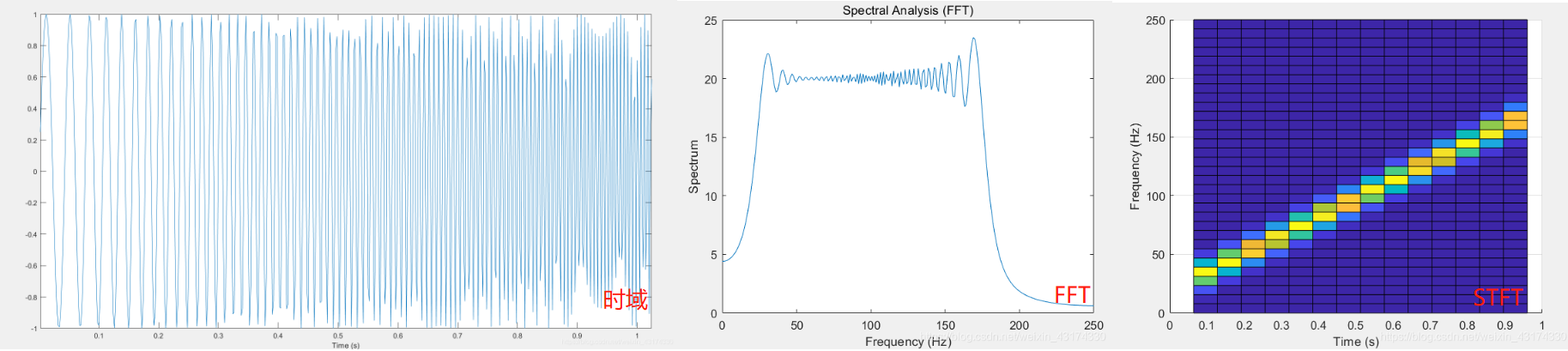
短時傅里葉變換輸出為三維圖形,分別為時間、頻率、強度三個軸(顏色即為對應時間、頻率下的信號強度),時間頻率軸上可明顯觀察到該信號的頻率成分,隨時間逐漸由20Hz線性增加到100Hz。
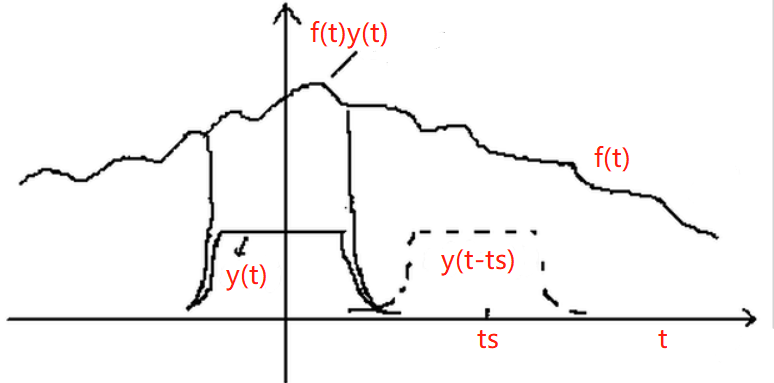
定義方窗函數為ywindow,窗長為width,將方窗函數向右平移了ts,再與原信號相乘,由于方窗函數除了中心的width部分是1外,其他部分都是0,這就相當于提取出了原信號在t=ts處,寬度為width的部分。因此,短時傅里葉變換可以表示為
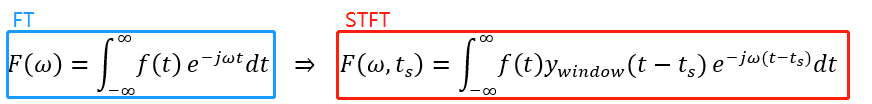
這里之所以e?jωt要變成e?jω(t?ts),是為了保證做FT的時候相乘的基函數具有統一性。
在線性代數中,基是描述、刻畫向量空間的基本工具。向量空間的基是它的一個特殊的子集,基的元素稱為基向量。向量空間中任意一個元素,都可以唯一地表示成基向量的線性組合。比如,向量空間的一個向量可以分解在x,y方向,同時在各個方向定義單位向量e1、e2,這樣任意一個向量都可以表示為a=xe1+ye2,這是二維空間的基。
在變換中,我們將原始信號乘上的信號稱為基函數。在傅里葉變換中,e-jwt是這個變換的基函數。STFT將基函數乘上一個方窗函數,形成了一個新的基函數:
![]()
假設用正弦函數sin(5t)表示原來的基函數e?jwt ,那么FT基函數和STFT基函數如下:
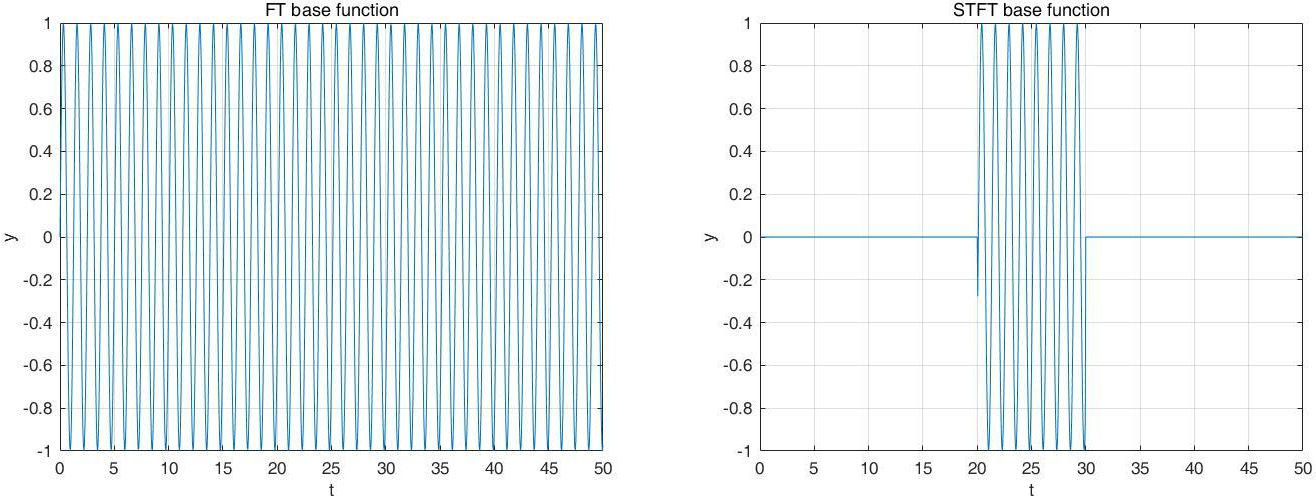
FT的基函數是在時域無限延伸的,因此,無論怎么平移,都是任分布在整個時域的,起不到分窗的作用。而STFT的基函數只在時域一段不為0,在剩下的時域都是0,因此,STFT的基函數的平移,就相當于自動加了窗子。STFT的本質是基函數的改變。
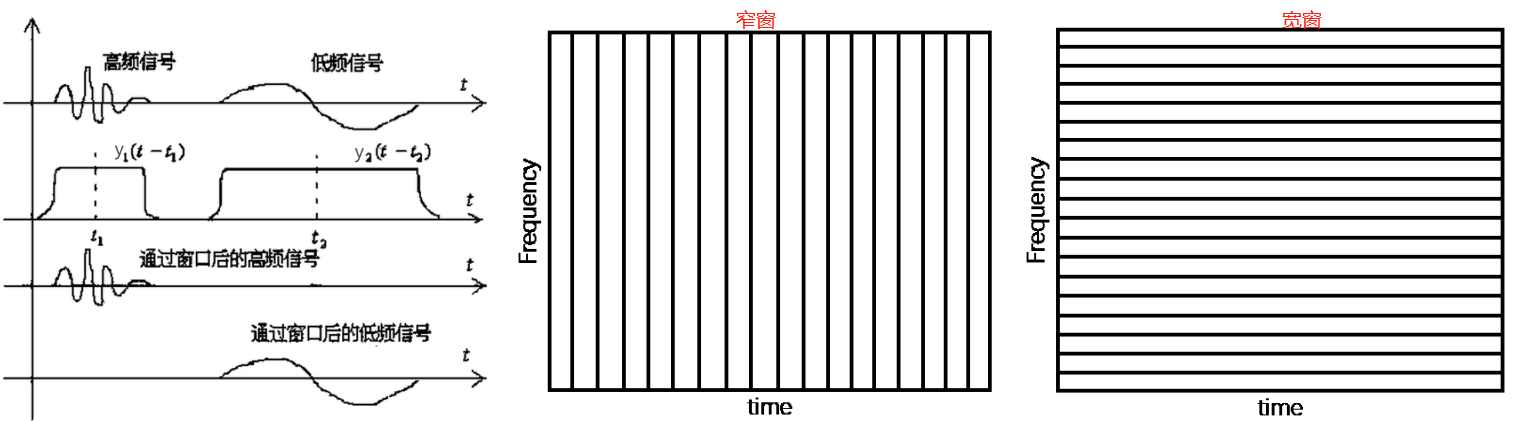
海森堡測不準原理: ΔtΔf>C,Δt為信號的時間不確定度,Δf為信號的頻率不確定度。即,我們永遠無法同時確定一個信號的確切時間和確切頻率。
- 對于低頻信號,為了更好地確定頻率,我們希望,時域區間寬一些,即時間不確定度Δt大一些,根據海森堡測不準原理,頻率不確定度Δf自然小一些;即低頻信號,我們希望:寬窗子,低的時域分辨率,高的頻域分辨率。
- 對于高頻信號,為了更好地在時域定位,我們希望,時域區間窄一些,即時間不確定度Δt小一些,根據海森堡測不準原理,頻率不確定度Δf自然大一些;即高頻信號,我們希望:窄窗子,高的時域分辨率,低的頻域分辨率。
高頻部分適合用小窗(短周期),低頻部分適合用大窗(長周期)。然而,在一次STFT中,窗口的寬度是固定,即時域分辨率是固定的,根據海森堡測不準原理,其頻域分辨率也是固定的。也就是說,不論高頻低頻,其時域和頻域分辨率都不可調,這是STFT的缺點。
1.3 連續小波變換
小波分析在時間域和頻率域同時具有良好的局部化性質,即在低頻部分具有較高的頻率分辨率和較低的時間分辨率,在高頻部分具有較高的時間分辨率和較低的頻率分辨率,因此有“顯微鏡”之稱。小波變換具有對信號的自適應能力,因而比傅里葉分析更適合處理非平穩信號。小波做的改變就在于,將無限長的三角函數基換成了有限長的會衰減的小波基。

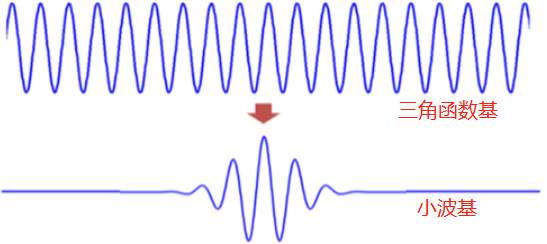
從公式可以看出,不同于傅里葉變換,變量只有頻率ω,小波變換有兩個變量:尺度a(scale)和平移量τ(translation)。尺度a控制小波函數的伸縮,平移量τ控制小波函數的平移。尺度就對應于頻率(反比),平移量τ就對應于時間。比如下圖,中間的小波s較小,相當于擠壓;右邊的s較大,相當于拉伸。
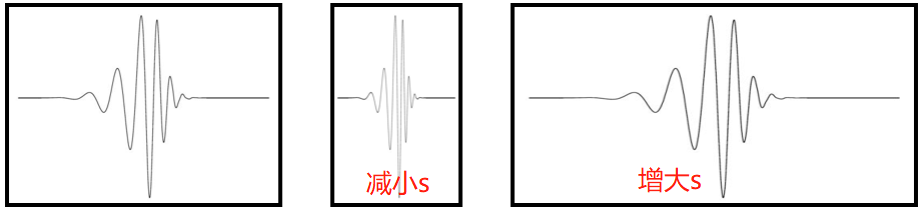
根據上面講的,滑動相當于分窗,窗的長度是基函數不為零的長度。中間的圖,s較小,相當于擠壓,頻率提高了,窗長變小了。右側的圖,s較大,相當于拉伸,頻率降低了,窗長變大了。正是我們需要的動態分辨率---低頻,寬窗,差的時間分辨率,好的頻域分辨率;高頻,窄窗,好的時間分辨率,差的頻域分辨率。
CWT的變換過程
Step1:把小波ψ(t)和原始信號f(t)的開始部分進行比較,計算系數C。系數C表示該部分信號與小波的近似程度,C的值越高表示信號與小波越相似。
Step2:把小波向右移,距離為τ,得到小波ψ(t-τ),重復步驟1。再把小波右移,得到小波ψ(t-2τ),重復步驟1。按上述步驟一直重復下去,知道信號f(t)結束。
Step3:拓展小波ψ(t),例如擴展一倍,得到的小波函數ψ(t/s),重復步驟1-2。
Step4:重復步驟1-3。
接下來我們對一個信號就行一次連續小波變換(CWT)。下圖中藍色部分為小波函數,黃色部分為信號。
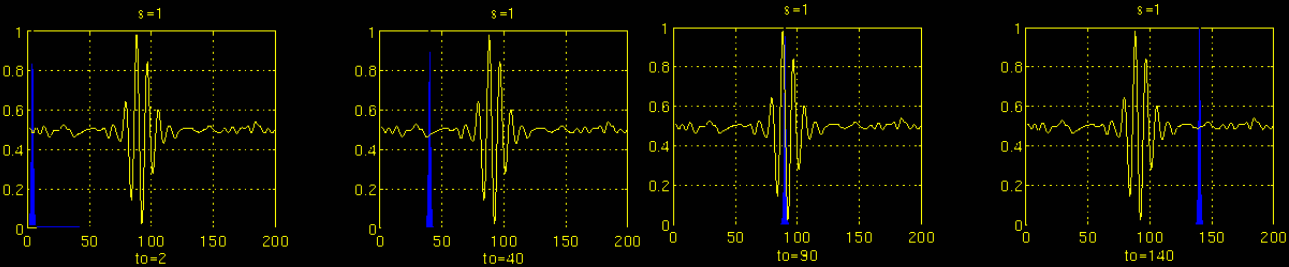
如上圖,選擇較小的s 對小波母函數進行縮放,此時小波函數頻率較高,窗子較窄(小波函數不為0的部分窄),用來篩選高頻部分。小波函數在時間軸上平移,每一次平移就先相乘,再積分,篩選出信號中與自己頻率相近的部分。此時,窗子較窄(小波函數不為0的部分窄),時間分辨率好,頻率分辨率差。
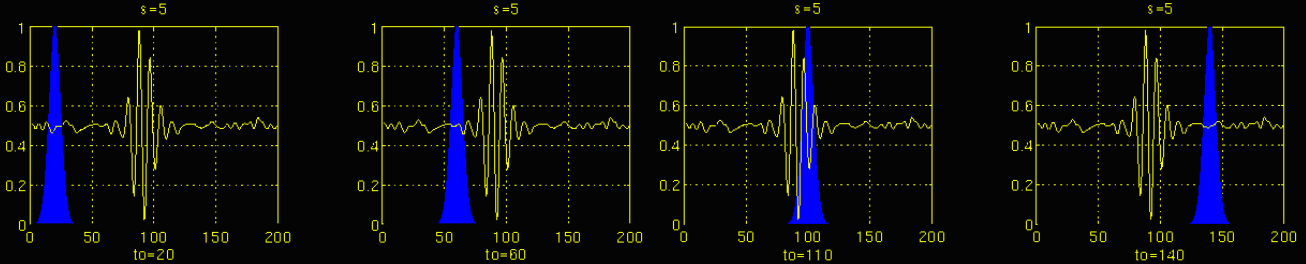
如上圖,將s 增大,對小波母函數進行縮放,此時小波函數頻率降低,窗子變寬(小波函數不為0的部分變寬),用來篩選中頻部分。小波函數在時間軸上平移,每一次平移就先相乘,再積分,篩選出信號中與自己頻率相近的部分。此時,窗子變寬了(小波函數不為0的部分變寬),時間分辨率變差,頻率分辨率變好。
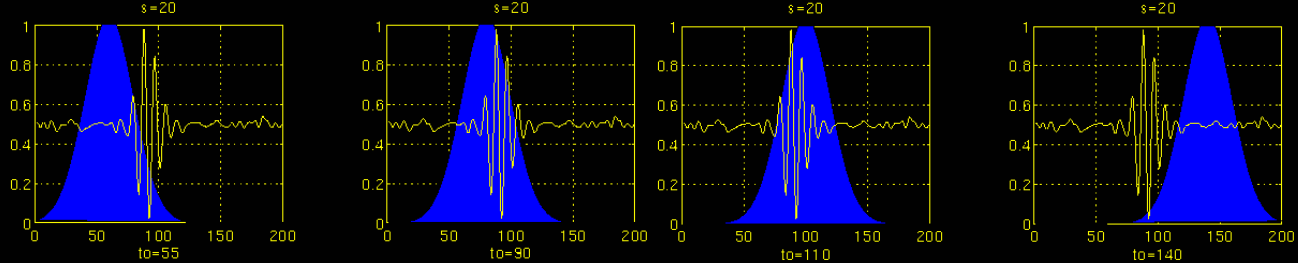
如上圖,將s 進一步增大,對小波母函數進行縮放,此時小波函數頻率再次降低,窗子更寬(小波函數不為0的部分更寬),用來篩選低頻部分。小波函數在時間軸上平移,每一次平移就先相乘,再積分,篩選出信號中與自己頻率相近的部分。此時,窗子很寬(小波函數不為0的部分很寬),時間分辨率差,頻率分辨率很好。
1.4 總結
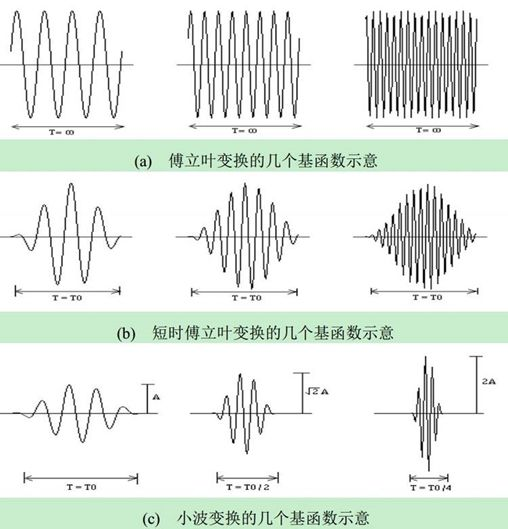
- FT的基函數,是分布在(?∞,+∞)的sin,cos,不具有緊支撐性,只能篩選頻率,使得FT完全喪失了時間信息,不具有時間分辨率。
- STFT的基函數,是用窗函數截斷的sin,cos (圖中是被高斯窗截斷的),具有了緊支撐性,時域平移等同于分窗,使得STFT既能篩選頻率,也能篩選時間。但是STFT基函數是:先確定頻率,再與窗函數相乘構成的。因此不同的頻率,具有同樣的時間和頻率分辨率。另外,窗函數的長短也比較難以確定。
- CWT的基函數,是小波函數,具有緊支撐性,時域平移等同于分窗,使得CWT既能篩選頻率,也能篩選時間。小波函數在改變頻率的時候,是通過“縮放”實現的,這使得小波函數在改變頻率的同時,改變了窗長。因此不同的頻率,具有不同的時間和頻率分辨率,實現了分辨率動態可調。

2 從小波變換到haar小波
2.1 離散小波變換
離散小波變換是對基本小波的尺度和平移進行離散化。為了解決計算量問題,縮放因子和平移參數都選擇2j的倍數。執行離散小波變換的有效方法是使用濾波器。該方法時Mallat再1988年開發的,叫做Mallat算法。這種方法實際上是一種信號的分解方法,在數字信號處理中稱為雙通道子帶編碼。
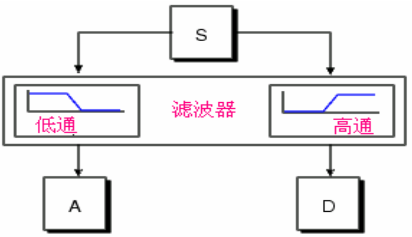
首先將原始信號作為輸入信號,通過一組正交的小波基分解成高頻部分和低頻部分,A表示信號的近似值(approximations),是大的縮放因子產生的系數,表示信號的低頻分量。D表示信號的細節值(detail),是小的縮放因子產生的系數,表示信號的高頻分量。然后將得到的低頻部分作為輸入信號,又進行小波分解,得到下一級的高頻部分和低頻部分,以此類推。隨著小波分解的級數增加,其在頻域上的分辨率就越高。這就是多分辨率分析(MRA,MultiResolution Analysis)。
離散小波變換可以被表示成由低通濾波器和高通濾波器組成的一棵樹。原始信號通過這樣的一對濾波器進行的分解叫做一級分解。信號的分解過程可以進行多級分解,分解級數的多少取決于要被分析的數據和用戶的需要。小波分解樹只對信號的低頻分量進行連續分解。把分解的系數還原成原始信號的過程叫做小波重構,數學上叫做逆離散小波變換。
任何小波變換的基函數,其實就是對母小波和父小波縮放和平移的集合。縮放倍數都是2的級數,平移的大小和當前其縮放的程度有關。小波系統有很多種,不同的母小波,衍生的小波基就完全不同。小波展開的近似形式是這樣的:
![]()
其中的ψj,k(t)就是小波級數,這些級數的組合就形成了小波變換中的基。
2.2 haar小波函數
最簡單的基函數是haar基函數,是由一組分段常值函數組成的函數集合,其父小波,也叫尺度函數(scaling function)
![]()
其中,i=0,1,...,(2j-1)。j是尺度因子,改變j使函數圖形縮小或者放大;i為平移參數,改變i使函數沿x軸方向平移。
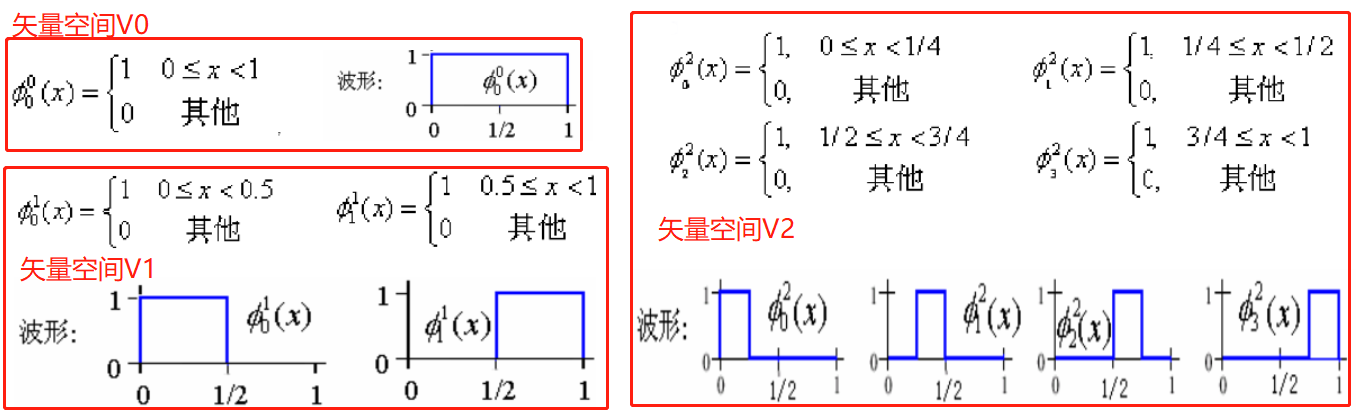
尺度函數可以代表一個空間,可以看出,假如有一個函數他屬于一個某空間,那你將其在時域上平移,它還是屬于這個空間。但如果你對它頻域的放大或縮小,它就會相應移到下一個或者上一個空間了。在矢量空間Vj中的每一個矢量被包含在矢量空間Vj+1中。我個人的理解,Φ00可以由Φ01和Φ11表示,Φ01可以由Φ02和Φ12表示等等,即任何尺度平移的尺度函數,都可以用更加精細的尺度層面上的尺度函數構建出來。j越大,尺度函數所做的時域上的平移幅度會越小,相應的在j子空間里面得到的f(t)表示粒度會很細,細節展現很多。不同的子空間有不同的分辨率,這就是用不同的分辨率去看目標信號。
母小波
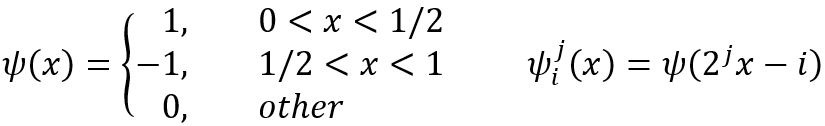
其中,i=0,1,...,(2j-1)。j是尺度因子,改變j使函數圖形縮小或者放大;i為平移參數,改變i使函數沿x軸方向平移。
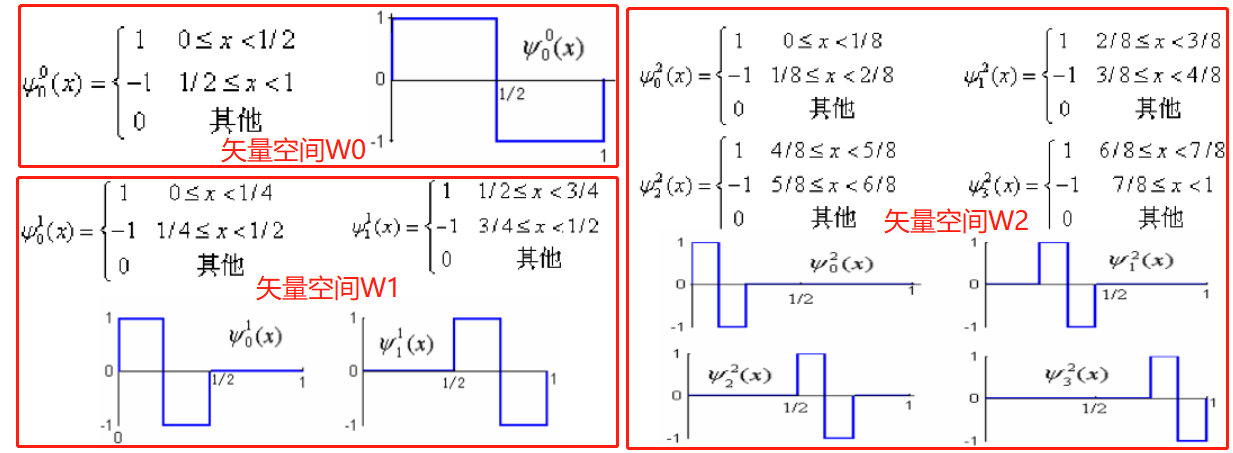
矢量空間Wj中的每一個矢量也被包含在矢量空間Wj+1中。下面我們對一個原始信號進行多解析度分析:
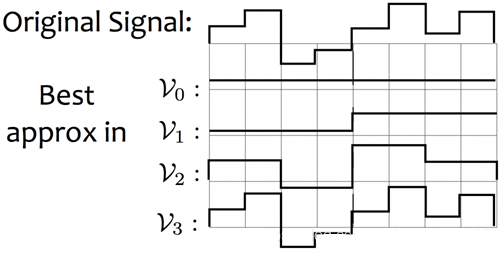
可以看出,在不同的子空間,對于同一個信號就有不同的詮釋。詮釋最好的是V3,完全不損失細節。這就是多解析度的意義。我們可以有嵌套的,由尺度函數演變的基函數集合,每一個集合都提供對原始信號的某種近似,解析度越高,近似越精確。
從上面也可以看出,直接用尺度函數就可以,或者母小波就可以還原信號。為什么要用兩個呢?
回顧上面的矢量空間圖,矢量空間W0中的小波函數,和V0中的尺度函數,可以構建V1中的尺度函數。矢量空間W1中的小波函數,和V1中的尺度函數,可以構建V2中的尺度函數。繼續推導下去,可以發現,尺度j下的小波函數,可以用來將Vj的基拓展到Vj+1中。這代表著,對任何一個子空間Vj,我們現在有兩種方法去得到它的正交基:(1)用它原本的基Φj,k(2)用上一級子空間的Φj-1,k和上一級子空間的小波函數ψj-1,k。第二種選擇能給我們帶來額外的好處,那就是我們可以循環不斷地用上一級子空間的尺度函數以及小波函數的組合來作為當前子空間的基。換句話說,如果針對V3這個子空間,它實際上就有四種不同的,但是等價的正交基。
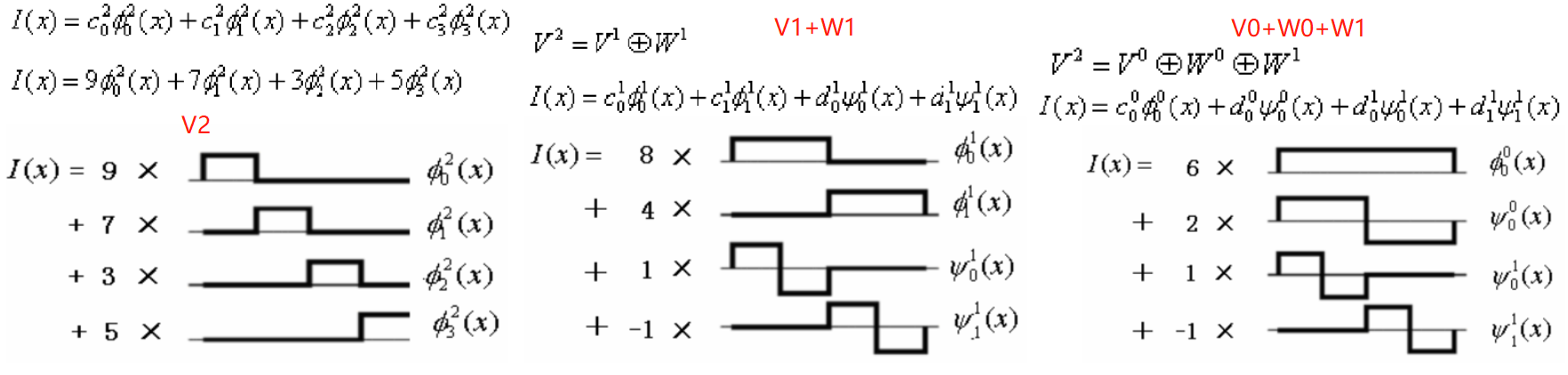
下面是V3子空間的第二種可選擇的正交基,V2的尺度函數和W2的小波函數:(上面沒歸一化,這邊歸一化了)
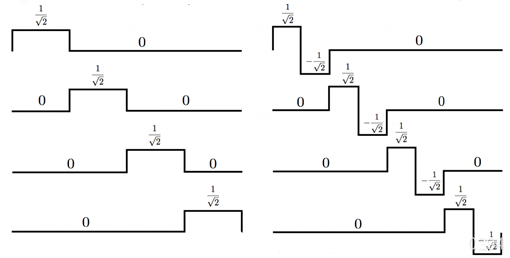
左邊這四個基和原始信號作內積,表征的是信號的平均。而右邊的這四個基和原始信號作內積則表征了在平均中丟失的信號細節。得益于此,多解析度分析能夠對信號在越來越寬的區域上取平均,等同于做低通濾波,而且,它還能保留因為平均而損失的信號細節,等同于做高通濾波。也就是說,尺度函數和小波函數背后的物理意義是:小波函數等同于對信號做高通濾波保留變化細節,而尺度函數等同于對信號做低通濾波保留平滑的形狀。
所有信號空間中的信號都可以寫成組成這個基的函數的線性組合:
![]()
對應的系數的計算和平常一樣:
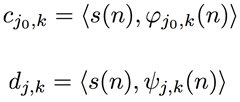
小波變換的基礎流程:
1. 選取合適的小波函數和尺度函數,從已有的信號中,反算出系數c和d。
2. 對系數做對應處理
3. 從處理后的系數中重新構建信號。
這里的系數處理是區別你的應用的重點。比如圖像或者視頻壓縮,就希望選取能將能量聚集到很小一部分系數中的小波,然后拋棄那些能量很小的小波系數,只保留少數的這些大頭系數,再反變換回去。這樣的話,圖像信號的能量并沒有怎么丟失,圖像體積卻大大減小了。
3 應用
3.1 一維harr小波分解
示例:求只有4個像素[9 7 3 5]的圖像的哈爾小波變換系數
步驟1:求均值(averaging),也叫Approximation。計算相鄰像素對的平均值,得到一幅分辨率比較低的新圖像,新的圖像的分辨率是原來的1/2,相應的像素值為:[8 4]
步驟2:求差值(differencing)。很明顯,用2個像素表示這幅圖像時,圖像的信息已經部分丟失。為了能夠從由2個像素組成的圖像重構出由4個像素組成的原始圖像,就需要存儲一些圖像的細節系數(detail coefficient),以便在重構時找回丟失的信息。方法是使用這個像素對的差值除以2,(9-7)/2=1,(3-5)/2=-1,結果為[1 -1]。到此為止,小波變換的一級分解結束,結果為[8 4 1 -1]。下面是小波變換的二級分解,即對低頻部分[8,4]進行分解。
步驟3:重復第1,2步,把由第一步分解得到的圖像進一步分解成分辨率更低的圖像和細節系數,結果為[6 2 1 -1]。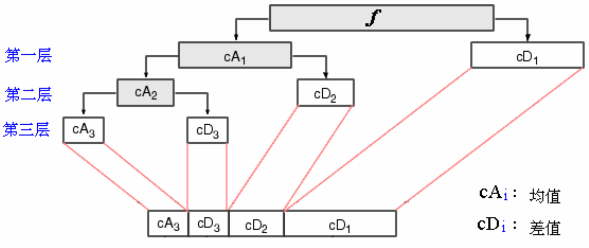
在變換過程沒有丟失信息,因為能夠從所記錄的數據中重構出原始圖像。首先在分辨率為1的圖像上重構出分辨率為2的圖像,在分辨率為2的圖像上重構出分辨率為4的圖像。通過變換之后產生的細節系數的幅度值比較小,這就為圖像壓縮提供了一種途徑,例如去掉一些微不足道的細節系數并不影響對重構圖像的理解。上面的分解其實就是之前說的,可以在不同的矢量空間用不同的基表示該圖像,用不同的分辨率去看圖像:
3.2 二維harr小波分解與重構
以離散余弦變換為基礎的JPEG標準算法,把圖片分塊處理會產生塊效應,在小波變換中,由于小波變換中適用的基函數的長度是可變的,因此無需把輸入圖像進行分塊,避免了塊效應。下圖為進行多級小波變換后,圖像各部分存放的是不同級數的小波系數。左上角的元素表示整個圖像塊的像素值的平均值,其余是該圖像塊的細節系數,h水平細節,v垂直細節,c對角細節。如果從矩陣中去掉圖像的某些細節系數,而且重構的圖像質量仍然可以接受,則可實現壓縮。具體做法是設置一個閾值,當細節系數小于這個閾值,就當做0來看待。
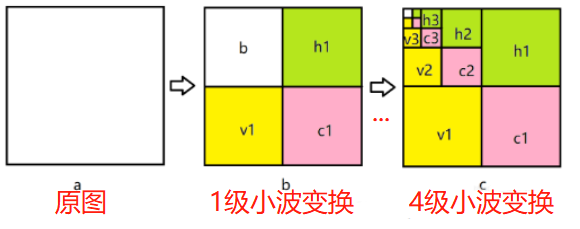
示例 小波圖像分解→閾值處理→重構
# include<opencv.hpp>
# include<iostream>
using namespace std;
using namespace cv;
Mat waveletTransform2D(Mat& img, int level) {
int width = img.cols;
int height = img.rows;
int depth = level;
int depthcount = 1;
Mat wavelet = Mat::zeros(img.size(), CV_32FC1);
Mat tmp = Mat::zeros(img.size(), CV_32FC1);
Mat imgtmp = img.clone();
imshow("src", imgtmp);
imgtmp.convertTo(imgtmp, CV_32FC1, 1.0);
while (depthcount <= depth)
{
height = img.rows / depthcount;
width = img.cols / depthcount;
// 水平
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width / 2; j++)
{
tmp.at<float>(i, j) = (imgtmp.at<float>(i, 2 * j) + imgtmp.at<float>(i, 2 * j + 1)) / 2; //水平方向求均值
tmp.at<float>(i, j + width / 2) = (imgtmp.at<float>(i, 2 * j) - imgtmp.at<float>(i, 2 * j + 1)) / 2; //水平方向求差值
}
}
// 豎直
for (int i = 0; i < height / 2; i++)
{
for (int j = 0; j < width; j++)
{
wavelet.at<float>(i, j) = (tmp.at<float>(2 * i, j) + tmp.at<float>(2 * i + 1, j)) / 2; //得到總均值和水平方向差值
wavelet.at<float>(i + height / 2, j) = (tmp.at<float>(2 * i, j) - tmp.at<float>(2 * i + 1, j)) / 2;//得到豎直方向均值和對角差值
}
}
imgtmp = wavelet.clone();
depthcount++;
}
return wavelet;
}
Mat invWaveletTransform2D(Mat& img, int level) {
int width = img.cols;
int height = img.rows;
int depth = level;
Mat tmp = Mat::ones(img.size(), CV_32FC1);
Mat wavelet = img.clone();
Mat imgtmp = img.clone();
while (depth > 0)
{
height = img.rows / depth;
width = img.cols / depth;
// 豎直
for (int i = 0; i < height; i+=2)
{
for (int j = 0; j < width; j++)
{
tmp.at<float>(i, j) = (imgtmp.at<float>(i/2, j) + imgtmp.at<float>(i/ 2+height / 2, j));
tmp.at<float>(i + 1, j) = (imgtmp.at<float>(i/2, j) - imgtmp.at<float>(i/ 2 + height / 2, j)) ;
}
}
// 水平
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j+=2)
{
wavelet.at<float>(i, j) = (tmp.at<float>(i, j/2) + tmp.at<float>(i, j/2+width/2));
wavelet.at<float>(i, j + 1) = (tmp.at<float>(i, j/2) - tmp.at<float>(i, j/2 + width / 2));
}
}
imgtmp = wavelet;
depth--;
}
return wavelet;
}
int main()
{
Mat img = imread("./2.tif", cv::IMREAD_GRAYSCALE);
//Mat img = (Mat_<uchar>(4, 4)<<1, 2, 3, 4,5,6,7,8,9,10,11,12,13,14,15,16);
// 1.小波變換
Mat wavelet = waveletTransform2D(img, 2);
// 2.閾值處理
for (int i = 0; i < wavelet.rows; i++)
{
for (int j = 0; j < wavelet.cols; j ++)
{
if (abs(wavelet.at<float>(i, j)) < 15)
wavelet.at<float>(i, j) = 0;
}
}
// 3.逆向小波變換
Mat dst = invWaveletTransform2D(wavelet, 2);
dst.convertTo(dst, CV_8UC1);
imshow("dst", dst);
waitKey(0);
return 0;
}
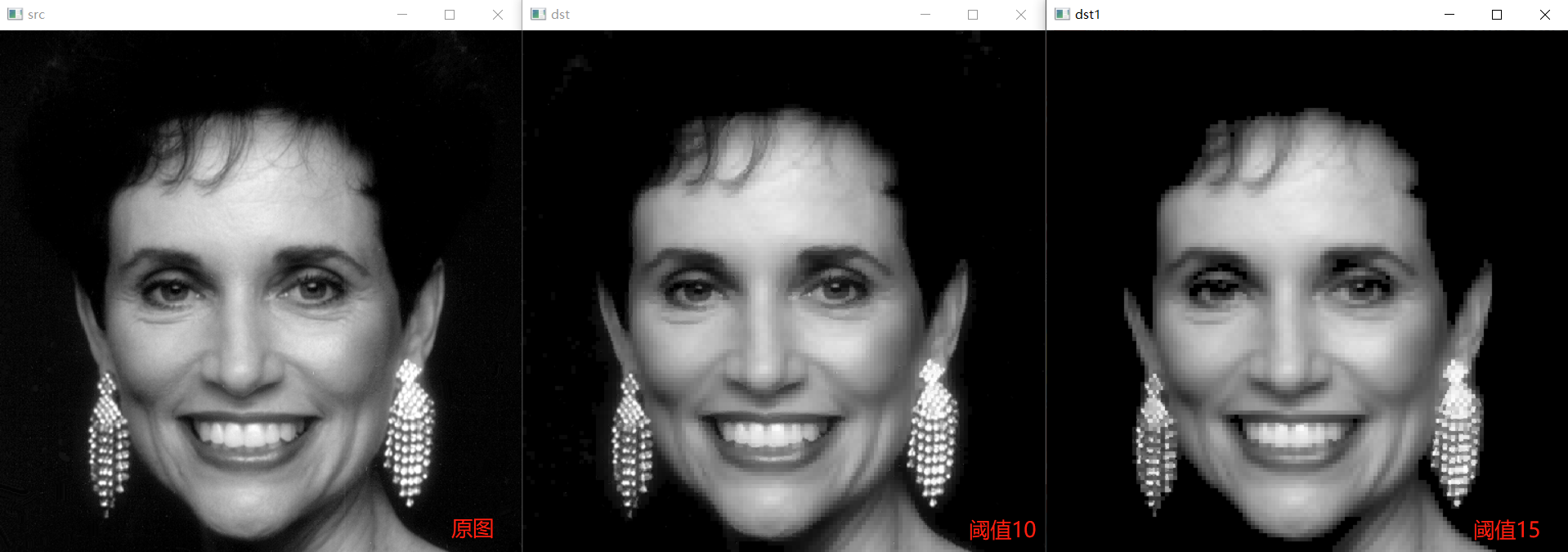
一般,有用信號表現為低頻信號或者是一些比較平穩的信號,而噪聲信號則通常表現為高頻信號,因此根據噪聲與信號在不同尺度(即不同頻率)上的小波譜具有不同表現的特點,將噪聲小波譜占主導地位的那些尺度上的小波分量去掉,而實現去噪。根據博客基于小波變換實現圖像增強:
- 小波分解后刪除高頻,即低通濾波,可以讓圖像變得平滑,濾除圖像中的噪聲。
- 小波分解后刪除低頻,即高通濾波,可以提取圖像邊緣,進而銳化圖像
- 小波分解后弱化高頻,增強低頻,可以增強對比度
該博客用matlab中的wavedec2函數 [c,s]=wavedec2(X,N,’wname’),c為各層分解系數,s為各層分解系數長度。c是一個行向量,c=[A(N)|H(N)|V(N)|D(N)|H(N-1)|V(N-1)|D(N-1)|H(N-2)|V(N-2)|D(N-2)|…|H(1)|V(1)|D(1)],A(N)代表第N層低頻系數,H(N)|V(N)|D(N)代表第N層高頻系數,分別是水平,垂直,對角高頻,以此類推,到H(1)|V(1)|D(1)。比如,設一級高頻系數為0,也就是c的最后部分H(1)|V(1)|D(1)置為0,對應c++這邊,就是將分解得到的圖像右半邊和下半邊都置為0。
參考:
1. 岡薩雷斯《數字圖像處理(第四版)》Chapter7(所有圖片可在鏈接中下載)
2. 短時傅里葉變換(Short Time Fourier Transform)
4. 小波變換(深入淺出)
6. 圖像處理-小波變換
9. 小波變換(wavelet transform)的通俗解釋
10. 基于小波變換實現圖像增強


 浙公網安備 33010602011771號
浙公網安備 33010602011771號