縱橫二劍

　　題目來源于《R語言的科學編程與仿真》第18章第18題，原題如下：

參數為$\alpha$的柯西分布的概率密度函數為

$$f_{X}(x)=\frac{\alpha}{\pi\left(\alpha^{2}+x^2 \right )},-\infty<x<+\infty$$

使用逆變換法編寫一個程序模擬柯西分布。現在考慮根據廣義拒絕法使用一個柯西包絡生成服從標準正態分布的隨機變量。

　　先介紹一下逆變換法。假設給定$U\sim U(0,1)$，并且我們準備模擬具有累積分布函數為$F_{X}$的連續型隨機變量$X$。令$Y=F_{X}^{-1}(U)$，那么我們有

\[F_{Y}(y)=P(Y\leqslant y)=P(F_{X}^{-1}(U)\leqslant y)=P(U\leqslant F_{X}(y))=F_{X}(y)\]

也即是，$Y$與$X$具有相同的分布。因此，如果我們能模擬服從$U(0,1)$分布的隨機變量，那么我們就能模擬任意已知$F_{X}^{-1}$的隨機變量$X$。

　　然后是廣義拒絕法。為了模擬密度函數$f_{X}$，我們假設有可以模擬的包絡密度$h$以及$k<\infty$使得$sup_{x}\frac{f_{X}(x)}{h(x)}\leqslant k$。具體步驟如下：

1.由$h$模擬$X$。

2.生成$Y\sim U(0,kh(X))$。

3.如果$Y<f_{X}(x)$那么返回$X$，否則返回步驟1。

　　為了提高廣義拒絕法的效率，我們需要選擇的$k$是越小越好。此題中，$h(x)=\frac{\alpha }{\pi \left ( \alpha ^{2}+x^2 \right )},f_{X}(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$。經過計算，當$k=\sqrt{2\pi}\frac{1}{\alpha}e^{\frac{\alpha^2}{2}-1},\alpha=1$時，k取得最小值。此時柯西分布的$\alpha$參數取值為1，剛好是標準柯西分布。

　　結合上述分析，具體代碼實現如下：

cauchy<-function(x,alpha){
  alpha/(pi*(alpha^2+x^2))
} # 柯西分布的概率密度函數
cauchy_sim<-function(alpha){

if(alpha<=0){

stop('alpha should be greater than zero')

}

U<-runif(1)

return(alpha*tanpi(U-1/2))

} # 逆變換法模擬柯西分布
k<-function(alpha){sqrt(2pi)/alphaexp(alpha^2/2-1)} # k是alpha的函數
norm_sim<-function(h,hsim,k,...){ # 用 ... 將參數alpha傳給h()和hsim()函數

while(TRUE){

x<-hsim(...)

x1<-h(x=x,...)

y<-runif(n=1,min=0,max=k(...)*h(x,...))

if(y<dnorm(x,mean=0,sd=1)){

return(x) # 利用return()終止循環

}

}

} # 模擬標準正態分布取值的函數
norm_sim(h=cauchy,hsim=cauchy_sim,k=k,alpha=1)

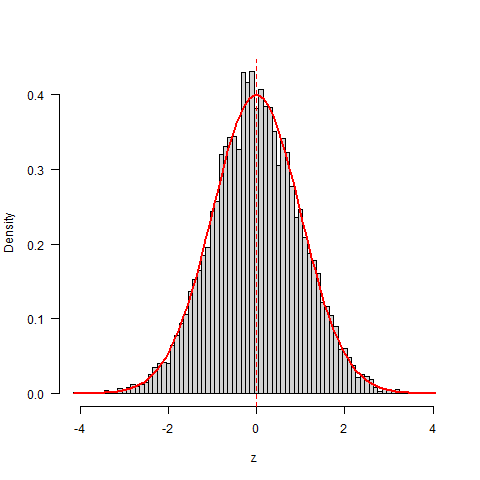
 　　下面畫圖比較模擬分布和真實分布的之間差異。

z<-replicate(1e4,
norm_sim(h=cauchy,hsim=cauchy_sim,
         k=sqrt(2*pi)/exp(0.5),alpha=1)) # 模擬一萬個觀測，用頻率估計概率
breaks<-seq(range(z)[1]-0.1,range(z)[2]+0.1,0.1)
par(las=1)
hist(z,breaks=breaks,freq=FALSE,main='') # 模擬分布直方圖
lines(breaks,dnorm(breaks,mean=0,sd=1),col='red',lwd=2) # 真實分布概率密度曲線
abline(v=0,col='red',lty=2)               

 　　圖形如下：