省選模擬賽
又雙叒開始記這個東西了,最好別又記一半不計了。
省選模擬4
15+4+60
A.我醉
這個 \([0,1000]\) 的值域很不對勁,想了很久,不出意外也是和正解沒有關系。打了個70的暴力還掛了。我醉。
考慮分討串的奇偶性并二分答案,對于當前待驗證的長度 \(L\) 用點分治+hash處理,具體地對于已經處理過的枝杈用一個什么東西存一下已有的hash值和深度二元組 \((H,dep)\),新引出來的枝杈就去查是否存在一個 \((H',L-dep)\) 使得兩段hash能拼一個回文串,復雜度 \(O(nlog^2n)\)。話是這么說的實現卻比較蛋疼。就比如說這個判斷回文就比較有說法因為 \(dep\) 和 \(L-dep\) 分別對應短鏈和長鏈所以先在長鏈里按 \(L\) 之類找一個對稱中心看一下滿不滿足子串是回文串,是了之后再用短鏈取匹配剩下的部分。
然后卡常啊很煩注意到不刻意構造的情況下答案很小所以答案上界削一下就能過了要不然跟暴力坐一桌。
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
#define MAXN 100005
#define ull unsigned long long
#define pii pair<ull,int>
#define mp make_pair
#define fi first
#define se second
using namespace std;
const ull p=13331;
ull pw[MAXN],has1[MAXN],has2[MAXN];
int n;
set<pii>sav,stac;
struct node{
int v,w,nxt;
}edge[MAXN<<1];
int h[MAXN],tmp;
inline void add(int u,int v,int w){
edge[++tmp]=(node){v,w,h[u]};
h[u]=tmp;
}
int ans=1;
bool vis[MAXN],F;
int lim,typ,L;
int siz[MAXN],dp[MAXN],root,sum;
inline void getrt(int u,int fa){
if(F)return;
dp[u]=0;
siz[u]=1;
for(int i=h[u];i;i=edge[i].nxt){
int v=edge[i].v;
if(vis[v]||v==fa)continue;
getrt(v,u);
siz[u]+=siz[v];
dp[u]=max(dp[u],siz[v]);
}
dp[u]=max(dp[u],sum-siz[u]);
if(dp[u]<dp[root])root=u;
}
inline void getdis(int u,int fa,int dep){
if(dep<=lim){
stac.insert(mp(has1[dep],dep));
pii tar=mp(has1[dep],L-dep);
if(*(sav.lower_bound(tar))==tar){
F=1;
return ;
}
}
else{
if(L&1){
ull Hpp=has1[dep-lim]*pw[dep-lim-1],Hps=has2[2*(dep-lim)-1]-has2[dep-lim-1];
if(Hpp==Hps){
stac.insert(mp(has1[dep]-has1[2*(dep-lim)-1]*pw[2*lim-dep+1],dep));
pii tar=mp(has1[dep]-has1[2*(dep-lim)-1]*pw[2*lim-dep+1],L-dep);
if(*(sav.lower_bound(tar))==tar){
F=1;
return ;
}
}
}
else{
ull Hpp=has1[dep-lim]*pw[dep-lim],Hps=has2[2*(dep-lim)]-has2[dep-lim];
if(Hpp==Hps){
stac.insert(mp(has1[dep]-has1[2*(dep-lim)]*pw[2*lim-dep],dep));
pii tar=mp(has1[dep]-has1[2*(dep-lim)]*pw[2*lim-dep],L-dep);
if(*(sav.lower_bound(tar))==tar){
F=1;
return ;
}
}
}
}
for(int i=h[u];i;i=edge[i].nxt){
int v=edge[i].v,w=edge[i].w;
if(v==fa||vis[v])continue;
has1[dep+1]=has1[dep]*p+w;
has2[dep+1]=has2[dep]+w*pw[dep];
getdis(v,u,dep+1);
}
}
inline void work(int u){
if(F)return ;
sav.clear();
sav.insert(mp(0,0));
for(int i=h[u];i;i=edge[i].nxt){
int v=edge[i].v,w=edge[i].w;
if(vis[v])continue;
has1[1]=has2[1]=w;
stac.clear();
getdis(v,u,1);
for(set<pii>::iterator it=stac.begin();it!=stac.end();it++)sav.insert(*it);
}
}
inline void solve(int u){
if(F)return ;
work(u);
vis[u]=1;
for(int i=h[u];i;i=edge[i].nxt){
int v=edge[i].v;
if(vis[v])continue;
sum=siz[v],root=0,dp[root]=n;
getrt(v,u);
solve(root);
}
}
inline bool check(int tar){
memset(vis,0,sizeof(vis));
F=0;lim=tar/2;
root=0,dp[root]=sum=n;
L=tar;
getrt(1,0);
solve(root);
return F;
}
signed main(){
freopen("name.in","r",stdin);
freopen("name.out","w",stdout);
pw[0]=1;
for(int i=1;i<MAXN;i++)pw[i]=pw[i-1]*p;
scanf("%d",&n);
for(int i=1,u,v,w;i<n;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,w);
}
int l=1,r=1650;
while(r>=l){
int mid=l+r>>1;
if(check(mid*2))ans=mid*2,l=mid+1;
else r=mid-1;
}
l=1,r=1800;
while(r>=l){
int mid=l+r>>1;
if(check(mid*2-1))ans=max(ans,mid*2-1),l=mid+1;
else r=mid-1;
}
printf("%d\n",ans);
return 0;
}
B.梧桐依舊
轉化題意為求 \(N*N\) 的矩陣 \(A\) 在滿秩矩陣 \(B\) 和 \(\times\) 構成的置換群中的不動點個數。轉化失敗遺憾離場說是。
把 Burnside 引理轉化一下
其中 \(|G|\) 就是滿秩矩陣 \(B\) 的個數,因為從一開始到 \(i\) 填充的向量要保證線性無關統計一下應該是
好玩的是考場上觀察出來答案總包含這么個形式,然后棄了。
然后求一下軌道即等價類個數,欽定秩的個數為 \(x\) 的時候求 \(B\times A\) 的不同個數,這個可以枚舉一下然后算
然后這個是 \(O(n^2)\),你反著跑一遍分母可以 \(O(n)\) 跑出來,復雜度就是 \(O(n)\)。
C.卿且去
白送60pts還是比較友善的。
60pts也要用的一個結論:顯然取 \((\lfloor\frac{n}{2}\rfloor,n]\) 是最優的,然后觀察數據范圍和設問應該是一個亞線性篩子題。
然后容易得到答案式子可以表示為
\(\pi(n)\) 可以 min25篩
,后面那一坨也可以 min25。
#include<bits/stdc++.h>
#define int long long
#define MAXN 200005
#define idx(x) ((x)<=V?id[0][(x)]:id[1][n/(x)])
using namespace std;
const int mod=998244353,inv2=499122177;
int n;
bool vis[MAXN];
int prime[MAXN],tot;
int id[2][MAXN],V,w[MAXN],cnt;
int g[MAXN];
inline void INIT(int n){
vis[1]=1;
for(int i=2;i<=n;i++){
if(!vis[i])prime[++tot]=i;
for(int j=1;j<=tot&&i*prime[j]<=n;j++){
vis[i*prime[j]]=1;
if(i%prime[j]==0)break;
}
}
}
inline int qpow(int base,int power){
int res=1;
while(power){
if(power&1)res=res*base%mod;
base=base*base%mod;
power>>=1;
}
return res%mod;
}
inline int S(int x,int i){
if(x<2||prime[i]>=x)return 0;
int res=(g[idx(x)]-i*inv2%mod+mod)%mod;
for(int j=i+1;j<=tot&&prime[j]*prime[j]<=x;j++){
for(int k=1,p=prime[j];p<=x;p*=prime[j],k++){
res=(res+(S(x/p,j)+(k>1?1:0))*inv2%mod+mod)%mod;
}
}
return res%mod;
}
int Pi,val,ans;
signed main(){
freopen("yyds.in","r",stdin);
freopen("yyds.out","w",stdout);
scanf("%lld",&n);
V=sqrt(n);
for(int l=1,r=0;l<=n;l=r+1){
r=n/(n/l);
w[++cnt]=n/l;
if(w[cnt]<=V)id[0][w[cnt]]=cnt;
else id[1][n/w[cnt]]=cnt;
}
INIT(V);
for(int i=1;i<=cnt;i++)g[i]=(w[i]-1)%mod;
for(int j=1;j<=tot;j++){
for(int i=1;i<=cnt&&prime[j]*prime[j]<=w[i];i++)
g[i]=(g[i]-g[idx(w[i]/prime[j])]+j-1+mod)%mod;
}
Pi=g[1];
for(int i=1;i<=cnt;i++)g[i]=g[i]*inv2%mod;
val=(S(n,0)-S(n>>1,0)+mod)%mod;
ans=qpow(2,Pi)*((n-(n>>1))-val+mod)%mod;
printf("%lld\n",ans);
return 0;
}
省選模擬5
10+30+100
A.蛋糕
然蛋題面。
考慮轉化方案為這樣的構造:對一條直線橫向地連到它相鄰的點上,然后順時針或者逆時針旋轉且不切到其他點,這一部分答案應為 \(4n(n-1)\),然后考慮兩點之間不單為橫/縱的情況,設兩個偏移為 \((i,j)\),有匯總答案:
后面一部分就莫反一下,推出來之后可以給前面的匯總成
這三個長得很篩子,前兩個分別分配一個 \(1,\text{id}\) 狄卷,是板子了,第三個可以參考這道題給一個 \((\text{id})^2\) 卷完杜教篩是一個
的形式,就可以做了。
B.巧克力
送30還是比較香的。
30pts可以用維護lst跑,先轉成tj里的nxt然后答案式子是
不可持久化的話,就拿set維護一下nxt的修改,對于答案計算就用線段樹維護全區間答案和最小的next以及它所屬的下標,信息合并可以線段樹二分一個左邊最靠右的比右邊min小的點然后合成新的右邊的min,重算一下答案,單次復雜度 \(O(logn)\)。詢問就從左到右合并區間求答案,總復雜度是 \(O(nlog^2n)\) 的。
然后加一下可持久化,相當于是把原先存nxt的set和其他數組換成主席樹,時間復雜度不變,空間卡一卡。
話是這么說的但是實現的細節挺惡心的,先擺個碼。
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
#define ll long long
#define MAXN 100005
using namespace std;
int n,q;
int a[MAXN],loc[MAXN],nxt[MAXN];
namespace Segment_Tree_ValIndex{
#define ls(p) tree[p].lson
#define rs(p) tree[p].rson
#define Ls(p) Tree[p].lson
#define Rs(p) Tree[p].rson
struct TREE{
int lson,rson;
int val;
}tree[(MAXN<<2)*18],Tree[(MAXN<<2)*18];
int rt[MAXN],tot;
inline void modify(int l,int r,int x,int k,int &p,int pre){
p=++tot;
tree[p]=tree[pre];
tree[p].val+=k;
if(l==r)return ;
int mid=l+r>>1;
if(x<=mid)modify(l,mid,x,k,ls(p),ls(pre));
else modify(mid+1,r,x,k,rs(p),rs(pre));
}
inline int lgetloc(int l,int r,int x,int p){
if(!tree[p].val)return 0;
if(l==r)return l;
int mid=l+r>>1;
int res=0;
if(x<=mid)return lgetloc(l,mid,x,ls(p));
res=lgetloc(mid+1,r,x,rs(p));
if(res)return res;
return lgetloc(l,mid,mid,ls(p));
}
inline int rgetloc(int l,int r,int x,int p){
if(!tree[p].val)return n+1;
if(l==r)return l;
int mid=l+r>>1;
int res=0;
if(x>mid)return rgetloc(mid+1,r,x,rs(p));
res=rgetloc(l,mid,x,ls(p));
if(res!=n+1)return res;
return rgetloc(mid+1,r,mid+1,rs(p));
}
int cnt,Rt[MAXN<<1];
inline void build(int l,int r,int &p){
p=++cnt;
if(l==r){
Tree[p].val=rt[l];
return;
}
int mid=l+r>>1;
build(l,mid,Ls(p));
build(mid+1,r,Rs(p));
}
inline void Modify(int l,int r,int x,int k,int &p,int pre){
p=++cnt;
Tree[p]=Tree[pre];
if(l==r){
Tree[p].val=k;
return ;
}
int mid=l+r>>1;
if(x<=mid)Modify(l,mid,x,k,Ls(p),Ls(pre));
else Modify(mid+1,r,x,k,Rs(p),Rs(pre));
}
inline int query(int l,int r,int x,int p){
if(l==r)return Tree[p].val;
int mid=l+r>>1;
if(x<=mid)return query(l,mid,x,Ls(p));
else return query(mid+1,r,x,Rs(p));
}
#undef ls(p)
#undef rs(p)
#undef Ls(p)
#undef Rs(p)
}
using Segment_Tree_ValIndex::Rt;
using Segment_Tree_ValIndex::rt;
using Segment_Tree_ValIndex::cnt;
using Segment_Tree_ValIndex::tot;
struct Segment_Tree{
#define ls(p) tree[p].lson
#define rs(p) tree[p].rson
struct TREE{
int lson,rson;
ll val,sum;
int nval,loc;
}tree[(MAXN<<2)*18];
int tot,rt[MAXN<<1];
inline int ask(int l,int r,int x,ll &y,int p){
if(l==r)return l;
int mid=l+r>>1;
if(tree[rs(p)].nval<x)return ask(mid+1,r,x,y,rs(p));
y+=tree[rs(p)].sum+tree[p].val;
return ask(l,mid,x,y,ls(p));
}
inline void push_up(int l,int r,int ls,int rs,int p){
if(tree[rs].nval<=tree[ls].nval){
tree[p].nval=tree[rs].nval;
tree[p].loc=tree[rs].loc;
tree[p].sum=tree[rs].sum;
return ;
}
tree[p].val=0;
tree[p].sum=tree[ls].sum+tree[rs].sum+(tree[p].val=(ll)tree[rs].nval*(tree[rs].loc-ask(l,r,tree[rs].nval,tree[p].val,ls))-tree[p].val);
tree[p].nval=tree[ls].nval;
tree[p].loc=tree[ls].loc;
}
inline void build(int l,int r,int &p){
p=++tot;
if(l==r){
tree[p].val=a[l];
tree[p].nval=nxt[l];
tree[p].loc=l;
return ;
}
int mid=l+r>>1;
build(l,mid,ls(p));
build(mid+1,r,rs(p));
push_up(l,mid,ls(p),rs(p),p);
}
inline void modify(int l,int r,int x,int d,int y,int &p,int pre){
p=++tot;
ls(p)=ls(pre),rs(p)=rs(pre);
if(l==r){
tree[p].nval=d;
tree[p].loc=l;
tree[p].val=y;
return ;
}
int mid=l+r>>1;
if(x<=mid)modify(l,mid,x,d,y,ls(p),ls(pre));
else modify(mid+1,r,x,d,y,rs(p),rs(pre));
push_up(l,mid,ls(p),rs(p),p);
}
inline int query(int l,int r,int x,int p){
if(l==r)return p;
int mid=l+r>>1;
if(x<=mid)return query(l,mid,x,ls(p));
else return query(mid+1,r,x,rs(p));
}
inline void change(int l,int r,int ul,int ur,int p){
if(l>=ul&&r<=ur){
push_up(l,r,p,tot+1,tot+1);
return ;
}
int mid=l+r>>1;
if(ur>mid)change(mid+1,r,ul,ur,rs(p));
if(ul<=mid)change(l,mid,ul,ur,ls(p));
}
}ST;
#define loc(p) ST.tree[p].loc
#define nval(p) ST.tree[p].nval
#define sum(p) ST.tree[p].sum
#define val(p) ST.tree[p].val
int T;
ll lans;
signed main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]),loc[i]=n+1;
for(int i=n;i>=1;i--){
nxt[i]=loc[a[i]];
loc[a[i]]=i;
Segment_Tree_ValIndex::modify(1,n,i,1,rt[a[i]],rt[a[i]]);
}
ST.build(1,n,ST.rt[0]);
Segment_Tree_ValIndex::build(1,n,Rt[0]);
scanf("%d",&q);
for(int i=1,opt,x,l,r;i<=q;i++){
scanf("%d%d%d%d",&opt,&x,&l,&r);
l=(l+lans)%n+1;
r=(r+lans)%n+1;
if(opt==1){
++T;
ST.rt[T]=ST.rt[x];
Rt[T]=Rt[x];
int loc=ST.query(1,n,l,ST.rt[T]);
int p=Segment_Tree_ValIndex::query(1,n,val(loc),Rt[T]);
if(val(loc)==r)continue;
Segment_Tree_ValIndex::modify(1,n,l,-1,p,p);
Segment_Tree_ValIndex::Modify(1,n,val(loc),p,Rt[T],Rt[T]);
p=Segment_Tree_ValIndex::lgetloc(1,n,l,p);
if(p)ST.modify(1,n,p,nval(loc),val(loc),ST.rt[T],ST.rt[T]);
p=Segment_Tree_ValIndex::query(1,n,r,Rt[x]);
ST.modify(1,n,l,Segment_Tree_ValIndex::rgetloc(1,n,l,p),r,ST.rt[T],ST.rt[T]);
int tar=Segment_Tree_ValIndex::lgetloc(1,n,l,p);
if(tar)ST.modify(1,n,tar,l,r,ST.rt[T],ST.rt[T]);
Segment_Tree_ValIndex::modify(1,n,l,1,p,p);
Segment_Tree_ValIndex::Modify(1,n,r,p,Rt[T],Rt[T]);
}
else{
nval(ST.tot+1)=r+1;
sum(ST.tot+1)=0;
loc(ST.tot+1)=r;
ST.change(1,n,l,r,ST.rt[x]);
printf("%lld\n",lans=sum(ST.tot+1)+(ll)nval(ST.tot+1)*(loc(ST.tot+1)-l+1)-(ll)(l+r)*(r-l+1)/2);
}
}
return 0;
}
C.奶酪
喜歡簡單題放T3。
抽一條直徑出來。以一個直徑端點為根dp子樹直徑,求答案的時候分討一下。如果是非直徑邊肯定有一個答案就是直徑,另一個可以dp。如果是直徑邊那有一個答案可以dp,另一個答案就把根換到另一個直徑端點再dp一遍求出。
省選模擬6
100+10+25
A.鸕鶿
考慮把矩形按上端點排序,逐個插入即可實現一個踢隊尾的均攤效果,然而合并是不太容易的,用線段樹維護 \(x\) 坐標并分別在每個節點記錄完全覆蓋它的和在它之內的矩形,顯然這兩種元素在單個線段樹節點內可以相消(只需要 \(y\)) 相交,這樣的話時間復雜度是均攤 \(O(nlogn)\) 的,空間復雜度也是...吧。
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
#define MAXN 100005
#define M 2000005
using namespace std;
int n,top;
namespace MYYY_Fast_IO{
inline int read(){
int w{1},x{};
char c=getchar();
while(c<'0'||c>'9'){if(c == '-')w=-1;c=getchar();}
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0',c=getchar();
return w * x;
}
inline void write(int x){
if(x<0) x=-x,putchar('-');
if(x>9)write(x/10);
putchar(x%10+'0');
}
inline void writeln(int x){write(x);putchar(10);}
inline void writek(int x){write(x);putchar(' ');}
}
using namespace MYYY_Fast_IO;
struct node{
int x1,x2,y1,y2;
bool operator<(const node &pre)const{
if(x1!=pre.x1)return x1<pre.x1;
if(x2!=pre.x2)return x2<pre.x2;
if(y1!=pre.y1)return y1<pre.y1;
return y2<pre.y2;
}
}sq[MAXN],ans[MAXN];
bool del[MAXN];
int hp[M];
int refl[M],tot,lfer[M],cnt;
inline bool cmp(node pre,node b){
return pre.y2<b.y2;
}
inline bool check(int x,int y){
node pre=sq[x],b=sq[y];
return pre.y2>b.y1&&pre.y1<b.y2&&pre.x2>b.x1&&pre.x1<b.x2;
}
inline void merge(int x,int y){
sq[x].x1=min(sq[x].x1,sq[y].x1);
sq[x].y1=min(sq[x].y1,sq[y].y1);
sq[x].x2=max(sq[x].x2,sq[y].x2);
sq[x].y2=max(sq[x].y2,sq[y].y2);
}
struct Segment_Tree{
#define ls(p) p<<1
#define rs(p) p<<1|1
#define sav(p) tree[p].sav
#define stac(p) tree[p].stac
struct TREE{
vector<int>sav,stac;
}tree[MAXN<<3];
inline void modify(int l,int r,int ul,int ur,int id,int p){
stac(p).emplace_back(id);
if(l>=ul&&r<=ur){
sav(p).emplace_back(id);
return;
}
int mid=l+r>>1;
if(ul<=mid)modify(l,mid,ul,ur,id,ls(p));
if(ur>mid)modify(mid+1,r,ul,ur,id,rs(p));
}
inline bool fix(int p,int id){
int res=0;
while(!stac(p).empty()){
if(del[stac(p).back()])stac(p).pop_back();
else if(check(stac(p).back(),id)){
int u=stac(p).back();
del[u]=1;
merge(id,u);
res=1;
stac(p).pop_back();
}
else break;
}
return res;
}
inline bool update(int l,int r,int ul,int ur,int id,int p){
bool f=0;
while(!sav(p).empty()){
if(del[sav(p).back()])sav(p).pop_back();
else if(check(sav(p).back(),id)){
int u=sav(p).back();
del[u]=1;
merge(id,u);
f=1;
sav(p).pop_back();
}
else break;
}
if(f)return 1;
if(l>=ul&&r<=ur)return fix(p,id);
int mid=l+r>>1;
int res=0;
if(ul<=mid)res|=update(l,mid,ul,ur,id,ls(p));
if(ur>mid)res|=update(mid+1,r,ul,ur,id,rs(p));
return res;
}
}ST;
signed main(){
// freopen("T1i.in","r",stdin);
//freopen("T1o.out","w",stdout);
n=read();
for(int i=1;i<=n;i++){
sq[i].x1=read();
sq[i].x2=read();
sq[i].y1=read();
sq[i].y2=read();
hp[++tot]=sq[i].x1,hp[++tot]=sq[i].x2;
}
sort(hp+1,hp+1+tot);
for(int i=1;i<=tot;i++){
if(!refl[hp[i]])refl[hp[i]]=++cnt,lfer[cnt]=hp[i];
}
sort(sq+1,sq+1+n,cmp);
for(int i=1;i<=n;i++){
sq[i].x1=refl[sq[i].x1];
sq[i].x2=refl[sq[i].x2];
while(ST.update(1,cnt,sq[i].x1,sq[i].x2,i,1));
ST.modify(1,cnt,sq[i].x1,sq[i].x2,i,1);
}
for(int i=1;i<=n;i++){
if(del[i])continue;
ans[++top]=sq[i];
ans[top].x1=lfer[ans[top].x1];
ans[top].x2=lfer[ans[top].x2];
}
sort(ans+1,ans+1+top);
writeln(top);
for(int i=1;i<=top;i++)writek(ans[i].x1),writek(ans[i].x2),writek(ans[i].y1),writeln(ans[i].y2);
return 0;
}
/*
5
7 8 1 4
1 5 2 3
4 5 2 7
2 3 5 9
4 6 8 9
*/
B.雪雀
就是問你一個 \(3\times N\) 的矩陣的全點對最短路和,這個 3 顯然是有說法的,可以發現最短路一定僅會穿過一個 \(x=x_0\) 至多兩次,因為三次就是S型了會相鄰,一定不優,兩次的話相當于 \(x=x_0\) 的一側是一個U型。
考慮分治解決這個問題,每次從 \(n\) 這條邊劈開一個 \(x=x_0\),然后處理左右兩側的最短路和,比如現在整從左到右的,線左右側六個點從上到下是 \(L_1,R_1,L_2,R_2,L_3,R_3\),根據上面的結論在這條線上只會存在 \(L_i\rightarrow R_i\) 的路徑,然后就要求他們仨分別負責了哪些路徑的最短路,這個你直接寫個最短路就行了。
后面忘了,嘻嘻。
C.燕鷗
這個是打表找規律題。
假設不進行欽定發現序列會以一個 \(a_i=3(a_{i-1}+1)\) 的規律清零,這樣零點個數是 \(O(log_3n)\) 的,且兩個零點之間的序列成波動狀,這個求區段就會很簡單,改完之后發現這個 \(a_i\) 其實沒什么變化所以你 \(O(nlog_3n)\) 就能枚舉修改下標跑完。然后更牛逼的是兩個零點間的這些元素你挑一個原本要減的改一下會發現改完三格之內序列會恢復到一個相同的規律,除非說你改到這一段末尾了。然后求答案的時候你掃一下 \(a_i,a_i+3,a_{i+1}-2\) 這三個位置特判一下,單個段詢問一下 \(O(log_3n)\),復雜度 \(O(log^2_3n)\)。
然后就是到 \(n,n-1\) 的時候恢復不回去了所以你特判一下。
省選模擬7
100+50+0,致敬傳奇模擬賽之排行榜分數極差15pts。
A.電車
改一個非質數的話質數那塊也是要改的,所以直接考慮質數的互換,兩個質數能交換當且僅當在 \([1,n]\) 范圍內影響到的數字個數相同,就是 \(\lfloor \frac{n}{p_i}\rfloor=\lfloor \frac{n}{p_j}\rfloor\),數論分塊一下同 \([l,r]\) 內的全部質數可以互換,沒了。
B.波長
大便。
設 \(f(x,d_i)\) 表示把最大子段和砍到 \(x\) 要在 \([1,i]\) 操作次數的前綴和,則 \(\forall i>j,\sum_{k=j}^ia_k-(d_i-d_{j-1})\le x,d_i\ge d_{i-1}\)。這個長得特別差分約束,但是比較蛋疼,設 \(D_i=d_i-\sum_{i=1}^ia_i\),則原式等價于
第二個就是可以選擇對一段連跳若干個 \(x\),這個段數是 \(O(n)\) 的,每次可以貪心取最大子段和然后將區間反轉。
進而答案的取值變為若干個一次函數形成一個下凸包 \(F(x)\),答案為對于直線 \(y=K\) 求 \(\sum_{i=1}^{F(i)=K}F(i)\),考慮維護一個線凸包,一段答案可以用等差數列求出。
綜上需要:一個線凸包的維護和一個支持查最大子段和和區間反轉的數據結構,考慮用線段樹維護區間最大子段和和區間最小子段和答案所在區間下標和反轉tag,std給了一種非常簡潔的實現。
#include<bits/stdc++.h>//34390
#define int long long
#define MAXN 100005
#define pii pair<int,int>
#define mp make_pair
#define fi first
#define se second
#define db long double
using namespace std;
int n,a[MAXN];
const int mod=998244353;
int K;
struct Segment_Tree{
struct data{
int v,l,r;
data(){}
inline data(int _v,int _l,int _r){v=_v,l=_l,r=_r;}
inline bool operator<(const data &X)const{return v<X.v;}
inline data operator+(const data &X)const{return data(v+X.v,l,X.r);}
};
struct seg{
data sum,lans,rans,xv;
seg(){}
inline seg(data _s,data _l,data _r,data _x){sum=_s,lans=_l,rans=_r,xv=_x;}
inline seg operator+(const seg &X)const{
return seg(sum+X.sum,max(lans,sum+X.lans),max(X.rans,rans+X.sum),max({xv,X.xv,rans+X.lans}));
}
};
struct Node{
Node *ls,*rs;
bool tag;seg X,N;
inline void push_up(){assert(ls&&rs);X=ls->X+rs->X,N=ls->N+rs->N;}
inline void down(){swap(X,N),tag^=1;}
inline void spread(){if(!tag)return ;ls->down(),rs->down(),tag=0;}
};
Node *rt;
vector<Node>tree;
inline void build(int l,int r,Node *&p){
tree.emplace_back();
p=&tree.back();
if(l==r){
p->X.sum=p->X.lans=p->X.rans=p->X.xv=data(a[l],l,l);
p->N.sum=p->N.lans=p->N.rans=p->N.xv=data(-a[l],l,l);
return ;
}
int mid=l+r>>1;
build(l,mid,p->ls);
build(mid+1,r,p->rs);
p->push_up();
}
inline void modify(int l,int r,int ul,int ur,Node *p){
if(l>=ul&&r<=ur){p->down();return ;}
p->spread();
int mid=l+r>>1;
if(ul<=mid)modify(l,mid,ul,ur,p->ls);
if(ur>mid)modify(mid+1,r,ul,ur,p->rs);
p->push_up();
}
}ST;
vector<pii>sav;
int ans;
inline void insert(int k,int b){//convexhull maintain
while(sav.size()>1){
pii A=sav.back(),B=sav[sav.size()-2];
db V=(db)(A.se-B.se)/(A.fi-B.fi);
if(V*k-b<=V*A.fi-A.se)sav.pop_back();
else break;
}
sav.emplace_back(mp(k,b));
}
signed main(){
// freopen("hacho14.in","r",stdin);
scanf("%lld%lld",&n,&K);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
ST.tree.reserve(2*n+5);
ST.tree.clear();
ST.build(1,n,ST.rt);
// printf("ced\n");
sav.emplace_back(mp(0,0));
int w=0;
for(int i=1;i<=n;i++){
if(ST.rt->X.xv.v<=0)break;
w+=ST.rt->X.xv.v;
insert(i,w);
ST.modify(1,n,ST.rt->X.xv.l,ST.rt->X.xv.r,ST.rt);
}
sort(a,a+1+n);
reverse(a,a+1+n);
for(int i=sav.back().fi+1;i<=n;i++)
if(a[i]<=0){
w+=a[i],insert(i,w);
}
// for(int i=0;i<sav.size();i++)if(sav[i].fi==34390){
// printf("What the fuck\n");
// return 0;
// }
int L=ceil((db)(sav.back().se-K)/sav.back().fi),R=0;
bool flag=0;
while(sav.size()>1){
pii A=sav.back();
sav.pop_back();
pii B=sav.back();
db V=(db)(A.se-B.se)/(A.fi-B.fi);
if (V<L){
L=ceil((db)(B.se-K)/B.fi);
continue;
}
R=ceil(V);
if(L<R){
if(!flag)ans=(K+(A.fi*L-A.se))%mod*L%mod,flag=1;
ans=(ans+(__int128)(L+R+1)*(R-L)/2%mod*A.fi-R+L)%mod;
}
L=R;
}
printf("%lld\n",(ans%mod+mod)%mod);
return 0;
}
C.捕獲
沒改嘻嘻。
省選模擬8
30+20+0,網絡流專題說是。
AGC031E
題面是二改的,令人忍俊不禁。
限制和數據范圍是難以處理的,所以用網絡流解決(?),比如現在考慮限制 \(L_i\) 不超過 \(b_i\) 個,可以認為第 \(b_i\) 個在 \(L_i\) 右側,進而就能求出對于一個維度的第 \(i\) 個點的坐標下界。
話是這么說的但是網絡流沒法四個維度一起考慮。考慮枚舉選了 \(K\) 個點那根據每個點可能的坐標范圍就可以對一個坐標求出一個點能否成為從左往右/從上往下第 \(x\) 個點。
所以你考慮兩個維度進行坐標的選,大概是這么個意思。
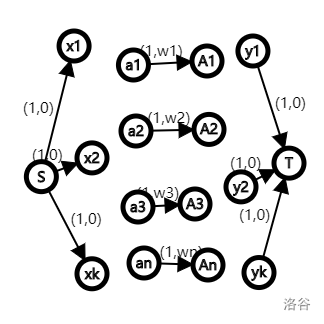
\(w_i\) 是 \(i\) 的價值,然后跑最大費用最大流,在maxflow=k后可以算答案。
CF1572D
顯然匹配點形成二分圖,按二進制1個數奇偶性分組之后左部點連一些右部點和匯點然后右部點連一個和超匯有K流量限制的假匯點就可以費用流。
但是邊數嚴重超時,發現一個人匹配后會踢掉 \(O(n)\) 條邊,但實際上分掉的是兩個人,所以匹配 \(k\) 次就會卡掉 \(k(2n-1)\) 種匹配,反過來看如果有 \(2nk\) 種匹配那應該就一定存在一組兩兩匹配了,所以只保留最大的 \(2nk\) 條邊即可。另外可以點優化,連邊的時候沒這個點再開點,就會很快,排序用快排,寫丑的桶排非常慢。
CF708D
一直以為給的圖是一個最大流圖哈哈。現在看是簡單題不知道為啥考場上沒一點想法。
考慮如何將原圖修改成可行的。對于 \(f\le c\) 顯然沒有別的邊的需求是不必改的,要改就是要么花 1 的費用增加或減少的流量 \(c-f,f\) 的,再就是用 2 的費用無限制擴大 \(f,c\)。對于 \(f>c\) 顯然要強制扣掉 \(f-c\) 先變成合法的,然后可以給變成一個 \([c,f]\) 建德滿流(這個就不用花費了) 或者砍成 \(f'<c\) 的不滿流,這個要費用,也可以花2無線擴大。
注意原圖中的流量是必須保證的,建完圖之后跑最小費用可行流。
省選模擬9
喜歡出原題。
100+70+100
A.染色
維護黑點到根的路徑,節點答案可以用換根求出,換根式子內的系數可以用樹剖維護,比原題簡單。
B.寢室管理
對于樹的情況:點分治后樹狀數組即可,也可以用多項式卷一下,沒必要。
對于基環樹的情況,拆一條環邊然后維護每個樹的答案,每個樹之間按距離乘一下就完事了。
C.基因合成
原題。[CERC2014]Virus synthesis。
省選模擬10
40+100+20
A.矩形
你先敲個50pts,把維護子段和的線段樹改成可持久化樹,一行一個樹然后set維護行最大連續區間*最大高度。掛分。
B.往事
喜歡出原題,記一下。
求Trie樹上lcs+lca深度(lcp)和的最大值。給Trie建一個廣義SAM,根據性質parent樹上兩點的lcs就是他們的lca長度,建完跑lca然后存一下可能作為答案的點跑set啟發式合并,set按dfn排完序可以直接找前后繼求答案。
C.時空穿梭
第一道場上出正解的數論,但是讓卡常了,而且正解沒時間打嘻嘻。
枚舉左下右上端點 \((i,j),(x,y)\),兩點之間的整點為 \((gcd(x-i,y-j)-1)\),貢獻就是 \(\binom{gcd(x-i,y-j)-1}{C-2}\)
考慮二維的情況,答案應為
帶入然后指標換一下
設 \(T=dx\),考慮 \(f(n,T)=\sum_{i=1}^n\lfloor\frac{i}{T}\rfloor\) 怎么算。
發現這個東西分為 \([1,T-1],[T,2T-1]...[xt,\lfloor\frac{n}{T}\rfloor T-1]\) 的整塊,這一部分每段長為 \(T\) 而且貢獻依次為 \(0,1,2..\lfloor\frac{n}{T}\rfloor-1\),剩下不足成段的拿分塊思路求即可。
后面一部分可以楊輝三角后調和級數預處理,答案擴展到 \(n\) 維就是
這樣就可以 \(O(Tnm)\) 求解了,再優化是我懶得看的,然后直接卡卡常就過了。
省選模擬11
0(100)+5+5
A.劃分
臥槽比賽好難沒分臥槽我他媽跟t1爆了臥槽我t1切了臥槽出分了臥槽ub是什么歌??臥槽rk1->rk倒1不嘻嘻。
這個看著就特別不能dp,還是二進制最優化題那就考慮貪心,經過構造發現,假設 \(n>m\) 可以前面全給b后面全給a,然后調整a,因為a終究更長所以收益總的來說大所以1就給a了0的話就拿掉b里先前最后的1這樣發現給a移位之后每個1最后表示出的數是一樣的所以一波操作的收益其實是+a加的那個1位-b扣的那個1位,顯然前者遞減后者遞增發現這樣調整不優之后就退出。
B.樹
不會。
C.劃分樹

省選模擬12
0+100+15
A.逆序對
白送56但是來不及寫了嘻嘻。
就是你先寫一個暴力狀壓,然后時空爆炸,然后考慮優化狀態數,可以通過詭異的數學證明把狀態數干成 \(3^{n/3}\),寫個hash表存狀態dp,或者寫一個長度進制數存狀態,跑的比較快。
B.網格圖
這不是我們燕鷗嗎怎么跑到這了。
n=3之前寫了,n=2的話一樣考慮分治,然后上面的較優當且僅當滿足一個偏序上樹狀數組,n=2本來跑的就快拿最短路寫得了就別分討大dp了。
C.種蘋果
詭異題目,這個叫做大容量小值域背包,因為物品大小只有12345然后直接對余數分類來dp,這個東西還滿足決策單調性你寫個單隊就行,也可以整體二分,后者比較短。
#include<bits/stdc++.h>
#define MAXN 300005
#define int long long
using namespace std;
const int mod=998244353,bas=20201205;
int n,b[MAXN],V,ans;
int dp[6][5*MAXN];
vector<int>W[6],sum[6];
inline void dfs(int now,int lst,int l,int r,int L,int R){
if(L>R)return;
int mid=L+R>>1,k=-1;
for(int i=max(l,mid-(int)W[now].size()),xr=min(mid,r);i<=xr;i++)
if(k==-1||dp[now-1][i*now+lst]+sum[now][mid-i]>dp[now-1][k*now+lst]+sum[now][mid-k])k=i;
dp[now][mid*now+lst]=dp[now-1][k*now+lst]+sum[now][mid-k];
dfs(now,lst,l,k,L,mid-1);
dfs(now,lst,k,r,mid+1,R);
}
signed main(){
freopen("apple.in","r",stdin);
freopen("apple.out","w",stdout);
scanf("%lld",&n);
for(int i=1;i<=n;i++)scanf("%lld",&b[i]),V+=b[i];
for(int i=1,c;i<=n;i++){
scanf("%lld",&c);
W[b[i]].emplace_back(c);
}
for(int i=1;i<=5;i++){
sort(W[i].begin(),W[i].end(),greater<>());
int s=0;
sum[i].emplace_back(0);
for(int x:W[i])s+=x,sum[i].emplace_back(s);
}
for(int i=1;i<=5;i++){
for (int r=0;r<i;r++)dfs(i,r,0,(V-r)/i,0,(V-r)/i);
}
int hp=1;
for (int i=0;i<=V;i++){
hp=hp*bas%mod;
ans=(ans+hp*(dp[5][i]%mod)%mod%mod+mod)%mod;
}
printf("%lld",ans%mod);
return 0;
}
省選模擬13
65+24+40
A.區間
有一個事情就是記區間最大值為 \(V\),長度為 \(L\) 則這段區間最后等于的 \(2^x\) 滿足 \(V\le x \le V+\log L\),這個是好證的。
樹上全點對路徑問題考慮點分治怎么數組上子序列問題就忘了分治了,我是傻逼嗎。對于很大的值的取等可以用hash處理,光速冪預處理冪次。然后就是在序列上分治,跑出來一個最大值然后考慮短的一側對長側的貢獻。按上面的結論直接枚舉可能取等的和然后hash判貢獻。
B.圣誕樹
考場上一秒想到2sat,然后我一想感覺方案是難以得到的然后棄了。哈哈。
考慮這樣的建模:設 \(vdc_{i,u,1/0}\) 表示第 \(i\) 個禮物是否在節點 \(u\) 子樹中。在一節點則一定在節點父親,在節點一兒子則一定不在節點另外兒子,這個是基本的樹應該保證的。對于詢問發現位置可重,看似難以處理實則只需不刻意限制,考慮這樣:\(a\) 不在 \(c\) 子樹則 \(b\) 一定要在 \(c\) 子樹,\(a\) 在 \(c\) 的兒子的子樹則 \(b\) 一定不在那個子樹,前者就可以有效規避"a在b不在"狀連邊導致的無法處理兩者同在 \(c\) 或者一者在 \(c\) 另一者在子樹的問題。
連邊和逆反命題,對每個點從根往下一直找合法的兒子直到不能跳為止。
C.神奇國度
沒看懂。
省選模擬14
70+10(60)+0
打的啥。
A.數
墜機題,開考之后急的要死兩個小時沒分,糊了個70走人了,不知道在急什么。
列個不等式然后兩邊式子一提,貢獻可以枚舉 \(x-y,x+y\) 單獨計算,沒了。
B.樹
一眼輪狀病毒+polya。答案就是
\(F(d)\) 就是不考慮旋轉同構時的答案,就是輪狀病毒那題。考場上一直算著 \(F(3)=18\) 然后就以為不是polya,唐唐的,剩二十分鐘頓悟了沒時間調。
需要一些手法,比如那個 \(\frac{1}{n}\) 因為模數任意就會特別蛋疼,然后就考慮一種手法就是把 \(mod\leftarrow mod*n\),最后給答案就能正常除了,又是從未出現的經典技巧呢。然后 \(F_i=3*F_{i-1}-F_{i-2}+2\) 這樣矩快是 27 常數的,然后不難發現 \(F_i=f_{2i}+f_{2i-2}-2\),其中 \(f_i\) 就是斐波那契數列,這樣矩快就會比較極速,還可以預處理 \(2^i\) 階系數矩陣用二進制拆解算答案,會快一些。
書
不難,但是沒改。
省選模擬15
60+0(10)+0(20)
喜歡打完暴力不拍。
A.單峰序列
60pts可以貪心,考場上一直在寫假,但是最后還是真了要不然保齡了。
從小到大填每次考慮向左向右較小的那個放。考慮動態加入的過程對左側是沒有影響的,右側則遞增,對于新加入的這個值影響的也是大于它的那一部分,狀態的影響其實可以用一個線段樹均攤實現。
B.劃分線段
這個是樹,但是合并就比較惡心了,因為貢獻的合并或者最優化沒法直接在當前節點處理,然后tj給出了一個比較牛逼的操作就是設 \(dp_{u,i,x,y}\) 表示的是節點 \(u\) 要確認 \(i\) 個段,當前 \(u\) 左右側是否有未補全的段,這個 \(i\) 是總不小于 \(siz_u\) 的,意思就是在確立 \(u\) 子樹的這些段的基礎上我又提前預留了 \(i-siz_u\) 個父親節點的位置。\(x,y\) 的有無就是說要不要有這個節點的一段延伸出去和其他一個節點拼起來。
對于葉子節點的初始化有
dp[u][0][0][0]=sav[u].se-sav[u].fi;
dp[u][0][0][1]=-sav[u].fi;
dp[u][0][1][0]=sav[u].se;
dp[u][0][1][1]=0;
第二維為了省空間自減了一個 \(siz_u\),如果不預留其他的段的話貢獻可以直接在當前節點處理成 \(r-l\),否則有殘留一段的情況下就只保留一部分前綴和的貢獻,如果兩邊都有的話就現不在這塊處理貢獻了,因為它這一段以后會和左右側分別合并。
對于合并兩個子樹 \(u,v\) 的過程,本質上是在做 \(dp_{u,{s1+s2+y},x,z}\leftarrow dp_{u,s1,x,y}+dp_{v,s2,y,z}\)。\(y\) 是要求同步的因為定義,而且如果都有預留段的話就在這個時候合并即段數+1。跑完輸出就行了。
另外轉移到最后一個子樹時要進行消預留段的操作就是
if(x)dp[u][i][0][y]=max(dp[u][i][0][y],g[typ][i][x][y]-sav[u].fi);
if(y)dp[u][i][x][0]=max(dp[u][i][x][0],g[typ][i][x][y]+sav[u].se);
還有一個比較手法的補足操作
if(x||y)dp[u][i][x][y]=max(dp[u][i][x][y],g[typ][i][x][y]);
這個的意思是,如果我的兩側有至少一個待補足的段,我可以讓它們在我中間就被補足,從而留下來至少一個空缺的段,此時有 \(dp_{u',i,x,y}\rightarrow dp_{u,i+1,x,y}\) 因為 \(siz_u=siz_{u'}+1\) 所以在移位后直接就是i->i但是如果沒有待補足的段我肯定不能憑空預留出來一個,所以有一個 x||y 的前置條件。
C.紅藍樹
想這樣一個事情:每個右括號的顏色都會影響到它右側的第一個左括號的顏色,顯然這是一個多對一的關系,進而這樣的影響關系當形成一棵樹,如果 \(r=n\) 的話就是整棵樹的一部分的某個藍點會讓它的整個根鏈變藍。
先預處理出這個樹,并每次遇到一個新的左括號就新開一個節點同時也是這個節點的 \(dfn\),這樣就實現了如果 \(dfn_x<dfn_y\) 則兩點在原序列的位置也一定滿足 \(x<y\),這個很重要,設想一下整棵樹的dfn是倒過來的。
現在不考慮反轉顏色的操作,則棧信息可以用線段樹來合并,具體地對于一個dfn 小的左子樹和大的右子樹(認為子樹已經合并完成),考慮對每個節點維護區間內最小和最大的藍色點dfn,即答案,則合并時相當于是額外加了左子樹最大->右子樹最小這一段的dfn的藍色點貢獻,這一部分可以直接倍增求出。
inline int getval(int l,int r){
int res=1;
if(!l)return 0;
for(int i=MAXK-1;i>=0;i--)if(father[i][l]<r)res+=(1<<i),l=father[i][l];
return res;
}
然后就可以合并了,查詢的時候查一下兩端最近的有效點的答案,最后把剩下來的一段 \([ans.xdfn,r+1)\) 單獨算個貢獻即可。
對于有修改的情況,你會發現這個線段樹的維護性能有點過于牛逼了,直接同時維護紅點和藍點的信息,反轉的時候打個rev標記就行,然后就做出來了。
關于一個corner case:當且僅當兩節點都有藍點的時候才進行合并貢獻,否則只進行最大最小值的維護和答案簡單相加,知道某一次出現兩側都有藍點時才進行合并,如果自始至終只有左側某一個藍點則會在最后對 \([ans.xdfn,r+1)\) 這一段處理時加上。



 浙公網安備 33010602011771號
浙公網安備 33010602011771號