【譯】使用SQL生成非均勻隨機數

    正如”隨機數的生成過程非常重要因此我們不能對其視而不見”(引自Robert R -橡樹嶺國家實驗室),我們希望占用您一點點寶貴的時間在基于SQL Server MVP Jeff Moden的成果的基礎上完成這項工作。對于使用SQL來產生隨機數來說，我們會重點講解從均勻分布隨機數(non-uniformly distributed random numbers)的基礎上生成非均勻分布隨機數(uniformly distributed random numbers);包括一些統計分布的基礎來幫你起步。

    正如我們所知，隨機數在仿真中非常重要(尤其是蒙特卡洛仿真法）,還有隨機數在密碼學以及其它高科技領域中也扮演了同樣重要的角色。除此之外在我們的SQL Server中有時也需要產生大量的隨機數據來測試SQL的性能。

    因為我并不是統計學家，因此我們這里僅僅來看用SQL生成并且能顯而易見的看出其隨機性的的隨機數字,而并不會深入到數學原理來看這個隨機性是真正的“隨機”還是“貌似隨機”我們的意圖是文章中算法的正確性以及這個算法在非關鍵領域是否足夠使用。

   通常來說，由均勻隨機數轉換成非均勻隨機數的技術是將均勻隨機數乘以累計分布函數(CDF)對于目標數據的反轉。但在實踐中，累計分布函數是否針對特定分布存在有效哪怕是接近的函數并不好估計。但幸運的是，比我們聰明許多的那幫家伙已經分析過了多個領域的多種分布函數我們可以直接拿來使用,這些函數可以滿足我們的大多數需求。

測試工具

    在我們的測試中，我們采用標準的SQL技術來使用偽URN(均勻分布隨機數)函數生成Float類型的參數傳給轉換函數.,我們將使用標量(Scalar)函數包括SCHEMABINDING關鍵字解決性能問題然而，或許你還想使用同等的表值函數來測試性能是否還可以進一步提升。首先，來生成測試數據。

-- Data definition and setup
DECLARE @NumberOfRNs   INT
       ,@Lambda        FLOAT     -- For the Poisson NURNs
       ,@GaussianMean  FLOAT     -- For the Normal NURNs
       ,@GaussianSTDEV FLOAT
       ,@LambdaEXP     FLOAT     -- For the Exponential NURNs
       ,@WeibullAlpha  FLOAT     -- For the Weibull NURNs
       ,@WeibullBeta   FLOAT
       ,@Laplaceu      FLOAT     -- For the Laplace NURNs
       ,@Laplaceb      FLOAT

SELECT @NumberOfRNs    = 10000
      ,@Lambda         = 4.0     -- Lambda for the Poisson Distribution
      ,@GaussianMean   = 5       -- Mean for the Normal Distribution
      ,@GaussianSTDEV  = 1.5     -- Standard Deviation for the Normal Distribution
      ,@LambdaEXP      = 1.5     -- Lambda for the Exponential Distribution
      ,@WeibullAlpha   = 1.0     -- Alpha (scale) for the Weibull Distribution
      ,@WeibullBeta    = 1.5     -- Beta (shape) for the Weibull Distribution
      ,@Laplaceu       = 4.0     -- Mu (location) for the Laplace Distribution
      ,@Laplaceb       = 1.0     -- Beta (scale) for the Laplace Distribution

--CREATE TYPE Distribution AS TABLE (EventID INT, EventProb FLOAT, CumProb FLOAT)

DECLARE @Binomial      AS Distribution
    ,@DUniform         AS Distribution
    ,@Multinomial      AS Distribution

-- Simulate a coin toss with a Binomial Distribution
INSERT INTO @Binomial
SELECT 0, 0.5, 0.5 UNION ALL SELECT 1, 0.5, 1.0

-- Events returned by this Discrete Uniform distribution are the 6
-- Fibonacci numbers starting with the second occurrence of 1
INSERT INTO @DUniform
SELECT 1, 1./6., 1./6. UNION ALL SELECT 2, 1./6., 2./6.
UNION ALL SELECT 3, 1./6., 3./6. UNION ALL SELECT 5, 1./6., 4./6.
UNION ALL SELECT 8, 1./6., 5./6. UNION ALL SELECT 13, 1./6., 1.

-- Events returned by this Multinomial distribution are the 5
-- Mersenne primes discovered in 1952 by Raphael M. Robinson
INSERT INTO @Multinomial
SELECT 521, .10, .10 UNION ALL SELECT 607, .25, .35 UNION ALL SELECT 1279, .30, .65
UNION ALL SELECT 2203, .15, .80 UNION ALL SELECT 2281, .2, 1.

   下面是測試工具，為了我們期望的目標分布生成NURNs(非均勻分布隨機數):

-- Create random numbers for the selected distributions
SELECT TOP (@NumberOfRNs)
     RandomUniform     = URN
    --,RandomPoisson     = dbo.RN_POISSON(@Lambda, URN)
    ,RandomBinomial    = dbo.RN_MULTINOMIAL(@Binomial, URN)
    ,RandomDUniform    = dbo.RN_MULTINOMIAL(@DUniform, URN)
    ,RandomMultinomial = dbo.RN_MULTINOMIAL(@Multinomial, URN)
    ,RandomNormal      = dbo.RN_NORMAL(@GaussianMean, @GaussianSTDEV, URN, RAND(CHECKSUM(NEWID())))
    ,RandomExponential = dbo.RN_EXPONENTIAL(@LambdaEXP, URN)
    ,RandomWeibull     = dbo.RN_WEIBULL(@WeibullAlpha, @WeibullBeta, URN)
    ,RandomLaplace     = dbo.RN_LAPLACE(@Laplaceu, @Laplaceb, URN)
 INTO #MyRandomNumbers
 FROM sys.all_columns a1 CROSS APPLY sys.all_columns a2
 CROSS APPLY (SELECT RAND(CHECKSUM(NEWID()))) URN(URN)

       接下來，我們將會逐個介紹每種分布類型，但是在此之前，首先闡述一下關于我們的測試工具你可能會問到的問題:

•     生成高斯分布NURN的算法需要兩個URN
•     我們使用RN_MULTINOMIAL 函數來生成三種不同的分布類型，因為其比另外兩種更加通用（會在文章后面詳細解釋）
•     在創建函數RN_MULTINOMIAL之前，首先需要創建自定義表類型。自定義表類型是在SQL Server 2008引入的，因此在SQL Server 2005中你不能使用這種方式，另一種替代方式是使用XML
•     我已經在文章附件中附加上了腳本，你首先運行Function.sql,然后運行NURNs.sql。生成100W的數據大概需要4.5分鐘（譯者注：在我的筆記本上跑了2.5分鐘）

均勻分布隨機數(Uniform Random Numbers) -----怎么個均勻法？

    因為接下來我們所有的數據分布都是基于均勻隨機數之上，所以我們來看一下這些由標準SQL生成的隨機數是怎么個均勻法。如果這些所謂的“均勻數”如果并不是那么”均勻”的話，那或多或少會對我們后面的結果產生影響。

    在｛0，1｝之間的URN概率很簡單，就是0.5。對于這一區間的方差則為1/12。對于使用SQL SERVER內置的AVG（）和VAR()函數來匯總我們生成的100W條數據。結果和我們期望的差不多。

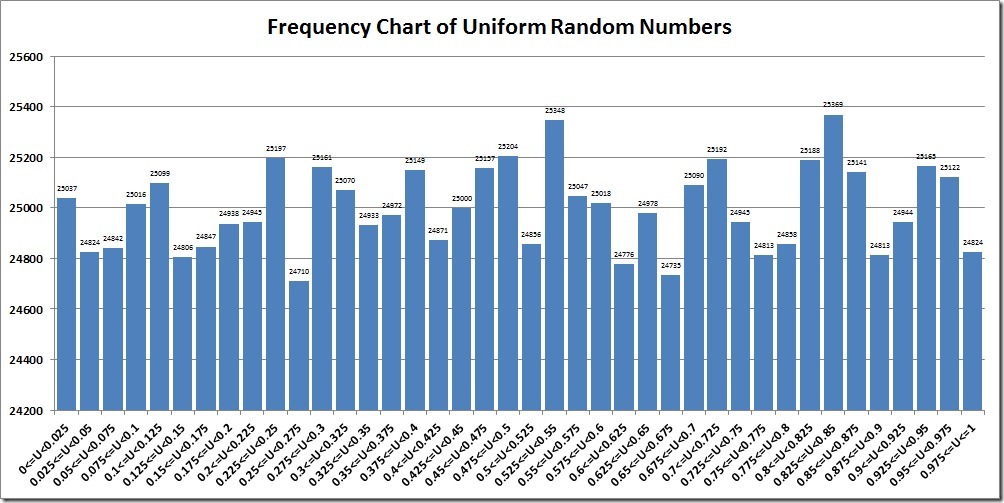
    下面的柱狀圖可以清晰的看到對于我們預定義區間的數據的分布：

    正如我們所看到的結果，雖然結果并不是非常的“標準”但是已經足夠對于我們這種并不需要那么精確的測試了。這里需要注意的是，我經過多次測試選擇的上述結果，并沒有特別的選取某個結果，如果你自己跑一遍SQL,你會發現你得到的結果也差不多。

多項式隨機數

    在我們開始討論多項分布之前，我們首先看一下其它兩種類型的離散分布。

    人們所熟知的拋硬幣概率其實就是柏松分布。這種用來表示二選一（正面或者反面）發生的概率,返回0或者1（或是其它某個數）來表示事件是否發生(也可以理解成“成功”或”失敗”)。當然了，就拋硬幣而言出現正面和反面概率是對等的，都是50%。但是柏松分布也允許其它非50%的概率，畢竟人生不總是那么公平嘛。

    離散均勻分布則描述了多于2個事件，比如說仍骰子，每一面出現的概率都是相同的。當然，這也是和我們生成給定范圍內隨機整數的方法是類似的。Jeff Moden曾經在這里給出過描述。

    多項式隨機數比上述兩種分布類型還要寬泛，它模擬了在一系列事件中每一個單獨事件發生的概率并不相同的情況。

    記住，我們的事件并不必要是一系列簡單數字的集合，比如0，1，2，3。還可以是任何數字（包括負數）的集合.比如，在我們的多項式分布中我們選擇了由Raphael M. Robinson在1952年發現的梅森尼質數,對于我們的離散均勻分布來說，我們采用了以1為開始的斐波納契數列的前6個數。我們還可以通過修改用戶自定義表類型Distribution的EventID列由INT改為FLOAT來將事件改為FLOAT類型。

    現在我們來看上面我們所設立用于測試的三個表變量，我們可以發現:

•     @Binomial定義了兩個事件(0,1),事件發生的概率P為50%，事件不發生的概率為1-p
•     @DUniform定義了6個事件(1, 2, 3, 5, 8, 13)，就像扔骰子一樣，每一個事件的概率都是1/6
•     @Multinomial定義了5個事件(521, 607, 1279, 2203, 2281),每一個事件發生的概率各不同

CREATE FUNCTION dbo.RN_MULTINOMIAL
    (@Multinomial Distribution READONLY, @URN FLOAT)
 RETURNS INT --Cannot use WITH SCHEMABINDING
AS
BEGIN
    RETURN
        ISNULL(
            (   SELECT TOP 1 EventID
                FROM @Multinomial
                WHERE @URN < CumProb
                ORDER BY CumProb)
            -- Handle unlikely case where URN = exactly 1.0
            ,(  SELECT MAX(EventID)
                FROM @Multinomial))
END

    對于我們測試的每一種分布，我們都進行了大量的測試結果后概率百分比如下表:

RandomBinomial     BinomialFreq     EventProb   ActPercentOfEvents

0                  499778           0.5         0.499778000000

1                  500222           0.5         0.500222000000

RandomDUniform     DUniformFreq     EventProb   ActPercentOfEvents

1                  166288           0.166666    0.166288000000

2                  166620           0.166666    0.166620000000

3                  166870           0.166666    0.166870000000

5                  166539           0.166666    0.166539000000

8                  166693           0.166666    0.166693000000

13                 166990           0.166666    0.166990000000

RandomMultinomial  MultinomialFreq  EventProb   ActPercentOfEvents

521                99719            0.1         0.099719000000

607                249706           0.25        0.249706000000

1279               300376           0.3         0.300376000000

2203               149633           0.15        0.149633000000

2281               200566           0.2         0.200566000000

通過上面的表格不難發現，這個概率和我們所期望的概率基本吻合。

高斯(或正態)分布隨機數

    在最近的討論中,SSC論壇的會員GPO發帖詢問基于高斯（正態）分布生成隨機數的問題。所以我開始研究這個問題（這其實也是本篇文章的靈感來源）并使用了博克斯·馬勒變換方法,基于我的RN_GAUSSIAN函數,你可以忽視我在這個帖子中對于如何利用URN生成NURN的算法.

    高斯分布是一個連續分布,對于熟悉這種分布需要我們一點點解釋，它經常采用平均數附近的“標準”樣本進行分析。

     出了平均數之外，還必須指定標準偏差。下面的函數幫助我們認識能夠幫我們了解示例總體數據正態分布的形狀。

CREATE FUNCTION dbo.RN_NORMAL
    (@Mean FLOAT, @StDev FLOAT, @URN1 FLOAT, @URN2 FLOAT)
 RETURNS FLOAT WITH SCHEMABINDING
AS
BEGIN
    -- Based on the Box-Muller Transform
    RETURN (@StDev * SQRT(-2 * LOG(@URN1))*COS(2*ACOS(-1.)*@URN2)) + @Mean
END

    首先我們先來比較總體（期望）平均數和方差與示例平均數和方差的比較來看這兩者之間是否接近。

PopulationMean   PopulationSTDEV   SampleMean         SampleSTDEV

5                1.5               5.00049965700704   1.50020497041145


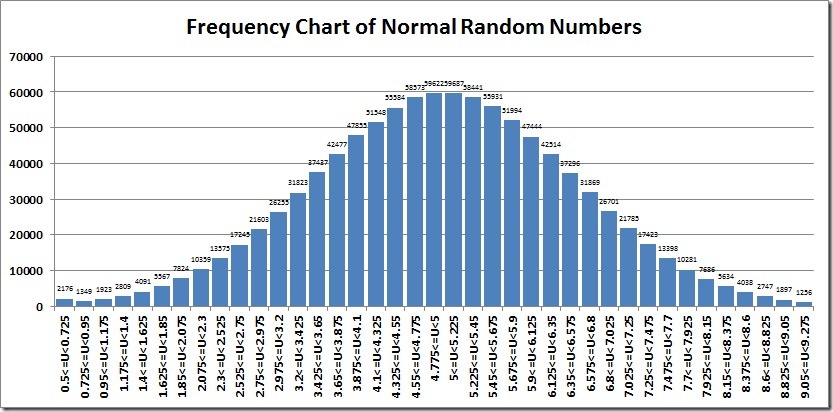
  然后，我們再來看圖表。圖中的間隔是加上或者減去3個平均數的標準差.

     讀者如果熟悉”正態”分布就會體會到這張圖是多么的”標準(正態)”,我們還認識到1,000,000中有998,596(99.86%)在我們的3個平均數的標準差之內。這也是我們所期望的結果。

指數隨機數

    指數隨機分布是可以用CDF(累計分布函數)進行分布，并且可以很容易的用接近的表達式表達出來的分布。指數隨機被應用于物理學,水理學，可靠性，等待時間等候論領域。

CREATE FUNCTION dbo.RN_EXPONENTIAL (@Lambda FLOAT, @URN FLOAT)
 RETURNS FLOAT WITH SCHEMABINDING
AS
BEGIN
    RETURN -LOG(@URN)/@Lambda
END

    首先要知道總體平均數是1/Lambda，標準方差是1/Lambda的平方,我們可以看到我們的總體平均數和方差和示例數據十分接近。

   PopulationMean   PopulationVAR   SampleMean   SampleVAR

   0.6667           0.4444          0.666        0.4444

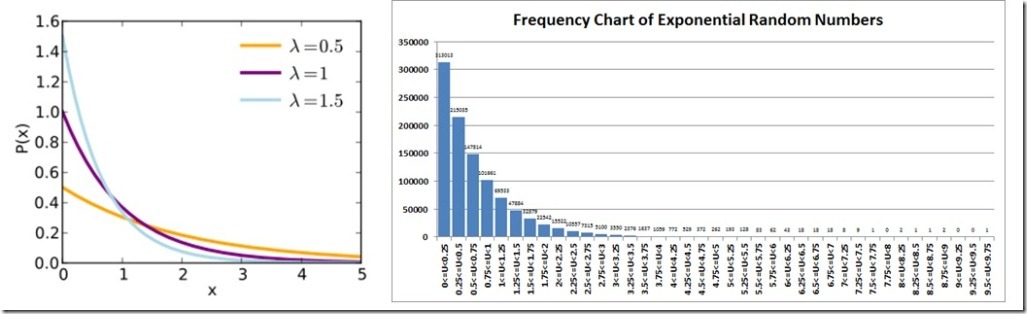
  我們可以看由維基百科上提供的概率密度曲線，當Lambda取值為1.5時(藍色的線)和我們的數據比較非常相似。

韋伯分布隨機數

    在大學中對韋伯分布已經小有研究,按照我的理解韋伯分布也是十分規律的，所以非常適合我們在這里生成非均勻隨機數(NURN).韋伯分布在很多統計和工程領域都有應用，包括天氣預報，保險，水理學,存活分析,可靠性工程（我教這門課的大學教授一定會為我驕傲的）以及其它領域。

    生成韋伯分布的公式我們可以在維基百科找到。而在我們這里實現這個方式的RN_WEIBULL函數實現起來也非常簡單。兩個參數分別為形狀和尺度參數(@WeibullAlpha,@WeibullBeta)

CREATE FUNCTION dbo.RN_WEIBULL (@Alpha FLOAT, @Beta FLOAT, @URN FLOAT)
 RETURNS FLOAT WITH SCHEMABINDING
AS
BEGIN
    RETURN POWER((-1. / @Alpha) * LOG(1. - @URN), 1./@Beta)
END

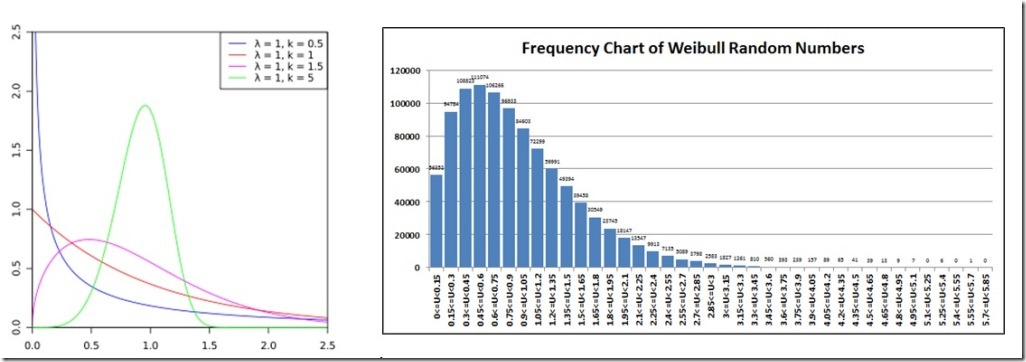
   韋伯分布的并不是那么容易計算，因為表達式使用了伽馬分布。下面是我們使用了形狀參數為1.0尺度參數為1.5的圖形，并與維基百科提供的圖形進行了對比。

拉普拉斯隨機數

    或許是因為我是一個geek，還是由于我們大學教這門課的老師非常牛逼。我非常喜歡拉普拉斯變換這門課。當我知道拉普拉斯還發明了拉普拉斯統分布時，我將這種分布加入到本文中來表達對拉普拉斯的敬意。

    拉普拉斯分布是一種連續分布,所幸的是，它的累計分布函數(CDF)非常簡單,在我們的函數中一個是位置參數，一個是尺度參數。

CREATE FUNCTION dbo.RN_LAPLACE (@u FLOAT, @b FLOAT, @URN FLOAT)
 RETURNS FLOAT WITH SCHEMABINDING
AS
BEGIN
    RETURN @u - @b * LOG(1 - 2 * ABS(@URN - 0.5)) *
        CASE WHEN 0 < @URN - 0.5 THEN 1 
             WHEN 0 > @URN - 0.5 THEN -1 
             ELSE 0 
        END
END

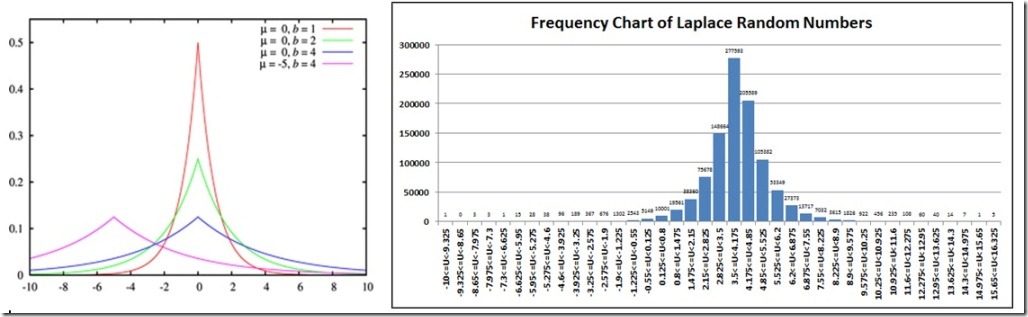
    拉普拉斯分布有著很容易計算的平均數(@u)和標準方差(2*@b^2)所以我們再一次將我們的總體樣本數據和示例數據進行比較。

   PopulationMean   PopulationVAR   SampleMean   SampleVAR

   4                2               4.0009       1.9975

  我們再一次使用我們的數據和維基百科提供的數據分布圖進行比較。在這里我們取@b=4(圖中紅線)

總結

    從本文的研究中我們得出結論，生成的非均勻隨機數基本是正確的，起碼和維基百科提供的數據比來說是正確的。此外我們還發現總體平均數和方差的對應關系。我們所有示例數據都在附件的EXCEL中。

    在自然界，人類和其它領域，隨機是無所不在的。而工具模擬了這些隨機性幫助我們在這個混亂的世界中找到規律。
    “創新其實就是在充滿不確定的自然界中引入規律”---- Eric Hoffer

    科學和工程的研究往往要使用隨機數來模擬自然界的現象。我希望我們的研究可以對這些領域的人有所幫助。

    對于那些好奇為什么我們不用柏松分布來產生非均勻隨機數的人。因為在SQL的內置函數中不允許我們生成多個隨機數（不使用NEWID() 和 RAND()是因為它們有“副作用”）,我們將繼續尋找在SQL Server中生成隨機數更好的辦法。
    本文闡述了在統計學中普遍存在的Alpha, Beta, Gamma和F分布。但是在生成非均勻隨機數背后的數學原理更加復雜，所以有興趣的高端讀者可以自行查找資料。
    我希望感謝那些勇猛無畏把本文讀完的讀者，尤其是那些一路跟著思考的讀者。謝謝它們對于非均勻隨機數的興趣和我們對于這個領域能提供更有用的例子。

------------------------------------------------------------------------------------------------------------

原文鏈接：Generating Non-uniform Random Numbers with SQL

Translated by CareySon

譯者注：因為本文的概念略多，所以里面對于英文版維基百科的鏈接我全部把鏈接替換到了百度知道。