2025杭電多校第九場 乘法逆元、阿斯蒂芬、計算幾何 個人題解
計算幾何
計算幾何
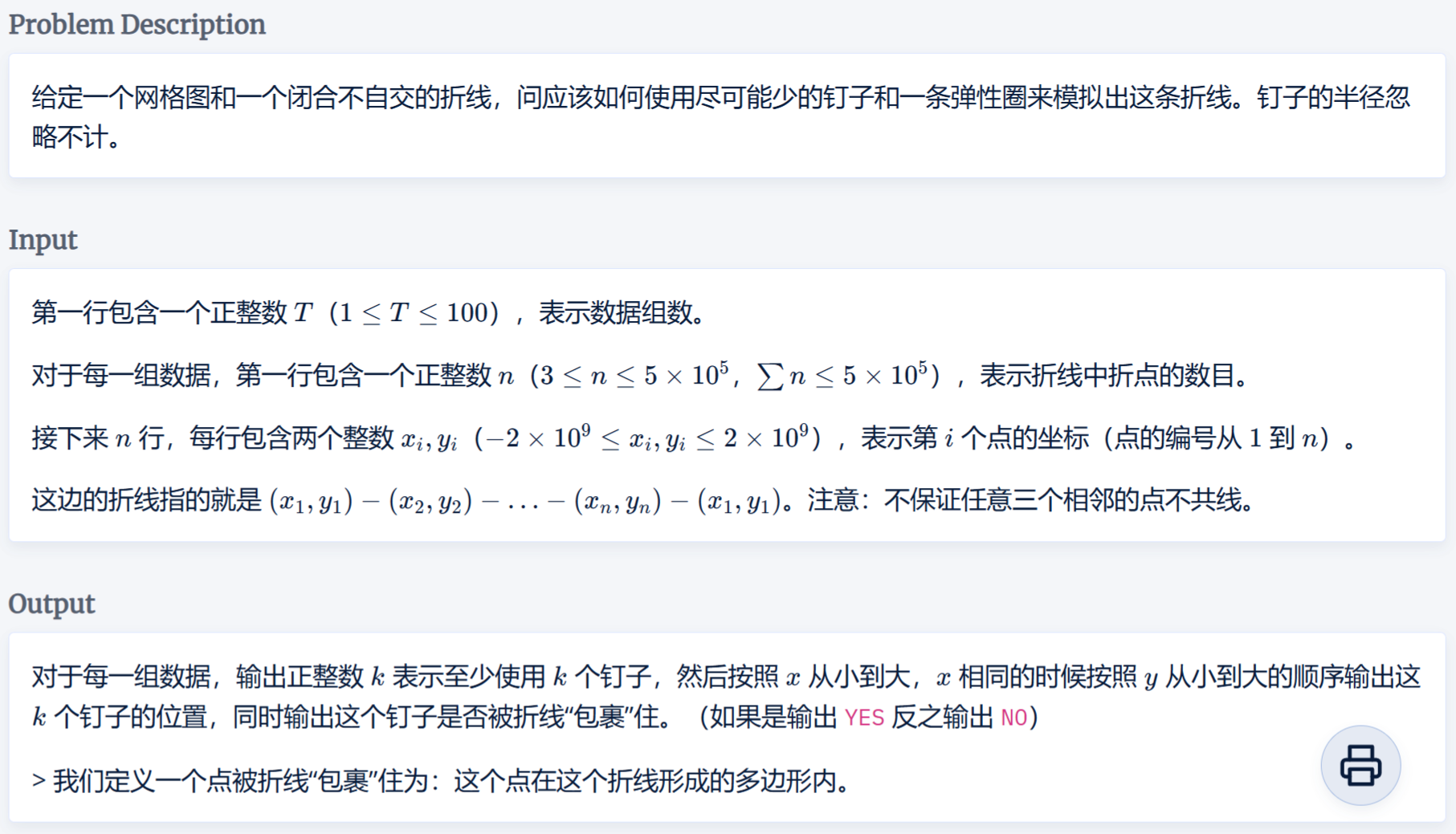
題目
思路
由于給定的是一條不自交的折線，因此可以直接沿著給定的折線來走
如果下一個點相對于當前的前進方向是向左，那么當前點標記為1，否則為0
判斷方向可以通過相鄰的兩個線段的向量的叉乘正負性
最后根據給定的折線是順時針還是逆時針來判斷1、0對應的是\(YES,NO\)
如何判斷給定的折線是順時針還是逆時針呢？
可以對相鄰的兩個點的向量進行叉乘后累加，計算這個多邊形的面積，最后判斷總面積的正負形就可以知道給定的折線是順時針還是逆時針了
特別需要注意的是，由于給定的點都是整數，叉乘計算出來的數也是整數，如果用板子里自帶的\(double\)類型的變量和函數，將會出現精度問題！！
賽時因為這個問題\(WA\)了8發
代碼實現
#include<iostream>
#include<vector>
#include<cmath>
#include<queue>
#include<algorithm>
#include<unordered_map>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr int inf = 1e9 ;
#define double ll
#define int ll
const double eps=1e-6;
const int N=5e5+5;
const double pi=acos(1.0*-1);
struct Vector {
double x, y;
Vector():x(0),y(0){}
Vector(double a, double b) :x(a), y(b) {}
bool operator<(const Vector&t)const{
if(x!=t.x)return x<t.x;
return y<t.y;
}
};
struct node{
Vector v;
int pd;
bool operator<(const node&t)const{
return v<t.v;
}
}a[N];
Vector operator+(Vector a, Vector b) {
return Vector(a.x + b.x, a.y + b.y);
}
Vector operator-(Vector a, Vector b) {
return Vector(a.x - b.x, a.y - b.y);
}
double operator*(Vector a, Vector b) {
return a.x * b.y - a.y * b.x;
}
double cross(Vector a, Vector b, Vector c) {
return (b - a) * (c - a);
}
double operator&(Vector a, Vector b) {
return a.x * b.x + a.y * b.y;
}
double dot(Vector a, Vector b, Vector c) {
return (b - a) & (c - a);
}
void eachT() {
int n;cin>>n;
int cnt=0;
rep(i,1,n){
cin>>a[i].v.x>>a[i].v.y;
}
Vector v=a[n].v-a[n-1].v;
Vector last=a[n].v;
int S=0;
rep(i,1,n){
Vector p,now;
S+=a[i].v*a[(i-1-1+n)%n+1].v;
p=a[i].v;
now=p-last;
if((v*now)==0){
a[(i-1-1+n)%n+1].pd=0;
last=p;
v=now;
continue;
}else if(v*now>0){
a[(i-1-1+n)%n+1].pd=1;
}else{
a[(i-1-1+n)%n+1].pd=-1;
}
cnt++;
last=p;
v=now;
}
sort(a+1,a+1+n);
cout<<cnt<<'\n';
if(S<0){
rep(i,1,n){
if(a[i].pd!=0){
cout<<a[i].v.x<<" "<<a[i].v.y<<" ";
if(a[i].pd==1)cout<<"YES\n";
else cout<<"NO\n";
}
}
}else{
rep(i,1,n){
if(a[i].pd!=0){
cout<<a[i].v.x<<" "<<a[i].v.y<<" ";
if(a[i].pd==-1)cout<<"YES\n";
else cout<<"NO\n";
}
}
}
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
ll t = 1;
cin >> t;
while (t--) {
eachT();
}
}
阿斯蒂芬
強聯通分量 #dfs
題目
思路
易知，對于一個強聯通分量，其中的點都可以互相抵達，那么能量就可以在這個塊中無限增長
而題目中有一個特別容易出錯的細節，沉寂操作只能不讓該節點的能量累積到\(T\)中，實際上能量還是在塊中無限增長的
也就是說，如果當前連通塊內有能量，那么連通塊能夠到達的點也都會能量無限增長，這些點也都必須要沉寂！
首先很明顯需要\(tarjan\)縮點，縮點時需要將點的權值以及點的大小記錄下來，縮點后的新圖是一個有向無環圖
為了沉寂連通塊也能到達的點，建新圖的時候需要反向建邊，相當于從能量源頭出發dfs
接下來在新圖上進行dfs：
數組\(vis[N]\)有三個狀態：
- \(vis[u]=1\)代表返回節點\(u\)的路上包含縮過的點，并且含有能量
- \(vis[u]=2\)代表返回節點\(u\)的路上都是沒縮過的點，并且含有能量
- \(vis[u]=3\)代表返回節點\(u\)的路上沒有能量
通過這樣三種狀態，我們可以一邊dfs一邊染色一邊更新答案
對于\(vis[u]=1\)的點，這個點是必須要沉寂的，可以直接算入答案中
偽代碼： - 入點：
- \(bool\)型變量\(val\)代表當前點\(u\)是否有能量，初始為\(0\)
- 遍歷所有子節點\(son\)：
- 如果\(vis[son]=3\)，兒子節點無能量，\(continue\)
- 如果\(vis[son]=2\)，兒子節點有能量，更新\(val\)，\(continue\)
- 如果\(vis[son]=1\)，兒子節點有能量并且路上包含縮過的點，\(vis[u]=1\)，\(break\)
- \(val\ |\ =dfs(son,u)\)，遞歸dfs
- 回溯：如果\(vis[son]=1\)，兒子節點有能量并且路上包含縮過的點，\(vis[u]=1\)，\(break\)
- 離點：
- 如果\(u\)本身就有能量，更新\(val\)
- 如果\(vis[u]\)還沒被更新過：
- 如果\(val=0\)，\(vis[u]=3\)，不包含能量
- 否則如果\(size[u]>1\)，\(vis[u]=1\)，包含縮過的點且有能量
- 否則\(vis[u]=2\)，不包含縮過的點但有能量
- 如果\(vis[u]=1\)，更新答案，加入\(size[u]\)個需要沉寂的點
- 返回\(val\)
代碼實現
#include<iostream>
#include<vector>
#include<cmath>
#include<queue>
#include<algorithm>
#include<set>
#include<stack>
#include<unordered_map>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
const int N = 5e5 + 5;
int n, w[N], b[N];
struct node {
vector<int>e;
int dfn, low, in, scc;
}a[N];
struct node1 {
set<int>e;
int siz, w;
}na[N];
stack<int>st;
int tot, cnt;
void tarjan(int u) {
a[u].dfn = a[u].low = ++tot;
st.push(u), a[u].in = 1;
for (auto& son : a[u].e) {
if (!a[son].dfn) {
tarjan(son);
a[u].low = min(a[u].low, a[son].low);
} else if (a[son].in) {
a[u].low = min(a[u].low, a[son].low);
}
}
if (a[u].dfn == a[u].low) {
int v;++cnt;
do {
v = st.top(), st.pop(), a[v].in = 0;
a[v].scc = cnt, ++na[cnt].siz;
na[cnt].w += w[v];
} while (u != v);
}
}
void build(int n) {
rep(i, 1, n) {
for (auto& son : a[i].e) {
if (a[i].scc != a[son].scc) {
na[a[son].scc].e.insert(a[i].scc);
}
}
}
}
unordered_map<int, int>vis;
int ans;
bool dfs(int u, int fa) {
bool val = 0;
for (auto& son : na[u].e) {
if (son == fa || vis[son] == 3)continue;//3 無能量
if (vis[son] == 2) { val |= 1;continue; }//2 無環有能量
if (vis[son] == 1) { vis[u] = 1;break; }//1 有環有能量
val |= dfs(son, u);
if (vis[son] == 1) { vis[u] = 1; }
}
val |= (na[u].w > 0);
if (vis[u] != 1) {
if (!val)vis[u] = 3;
else if (na[u].siz > 1)vis[u] = 1;
else vis[u] = 2;
}
if (vis[u] == 1)ans += na[u].siz;
return val;
}
void init() {
vis.clear();
ans = tot = cnt = 0;
while (st.size())st.pop();
rep(i, 1, n) {
a[i].e.clear();
a[i].dfn = a[i].in = a[i].low = a[i].scc = 0;
na[i].e.clear();
na[i].siz = na[i].w = 0;
}
}
void eachT() {
cin >> n;
init();
rep(i, 1, n)cin >> w[i];
rep(i, 1, n)cin >> b[i];
rep(i, 1, n) {
rep(j, 1, b[i]) {
int x;cin >> x;
a[i].e.push_back(x);
}
}
rep(i, 1, n) {
if (!a[i].scc)tarjan(i);
}
build(n);
rep(i, 1, cnt) {
if (vis[i] == 0)dfs(i, 0);
}
cout << ans << '\n';
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
ll t = 1;
cin >> t;
while (t--) {
eachT();
}
}
乘法逆元
數學 #位運算
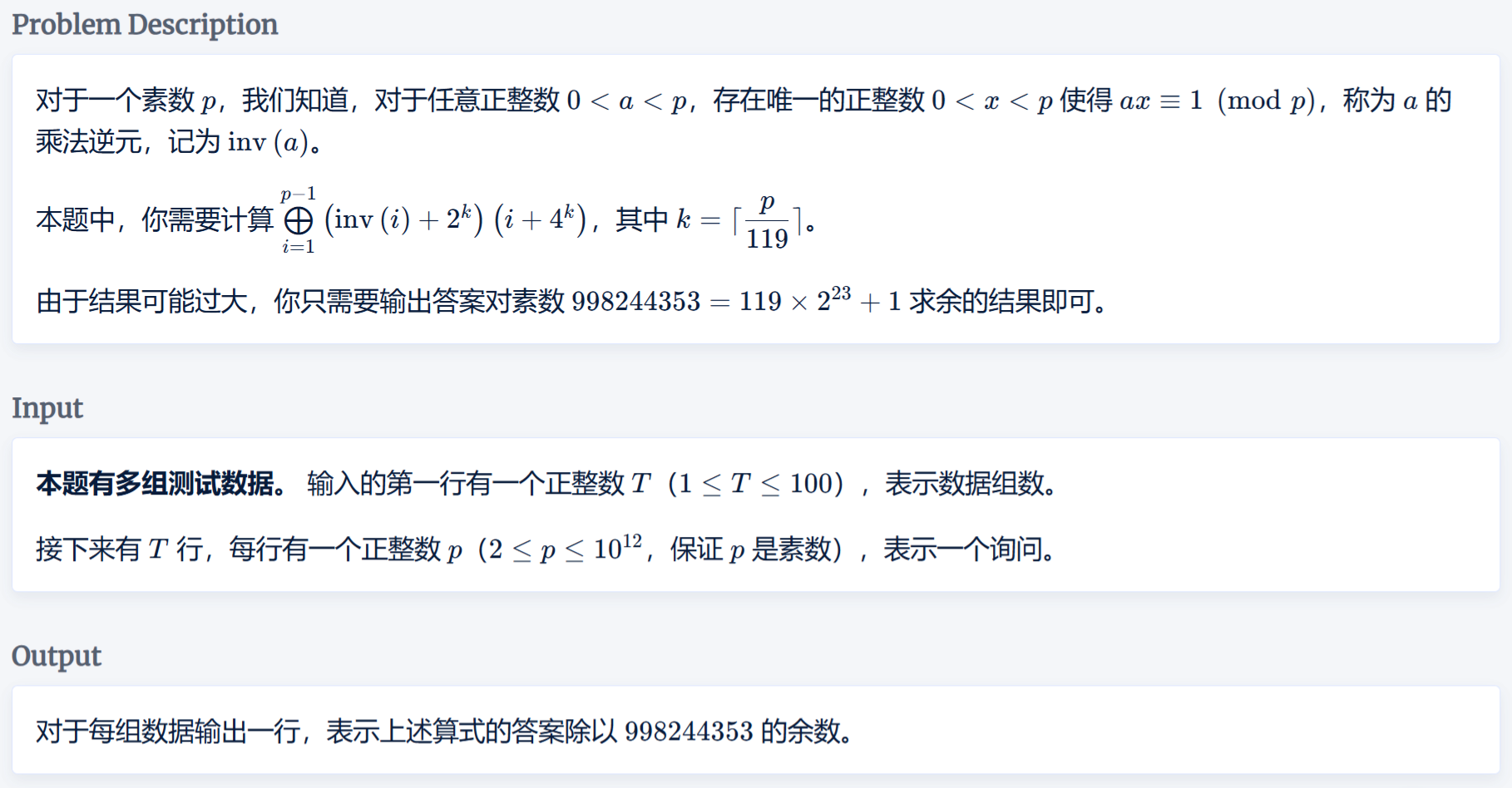
題目
思路
\[\begin{align}
&\bigoplus_{i=1}^{p-1}(inv(i)+2^k)(i+4^k)\mod{M}\\ \\
&=\bigoplus_{i=1}^{p-1}i\times inv(i)+i\times2^k+inv(i)\times 2^{2k}+2^{3k} \mod{M}
\end{align}
\]
當\(k\geq 23\)時，\(p\leq 23\times 119<2^{23}\leq 2^k\)
則有\(i<p<2^k,inv(i)<p<2^k\)
則有：
\[\begin{align}
\begin{array}{lc}
&i\times inv(i)&<i\times2^k&<2^k\times 2^k&<inv(i)\times2^k&<2^{3k} \\ \\
&0\sim 2^k &2^{k}\sim 2^{2\times k}& &2^{2\times k}\sim2^{3\times k}&2^{3\times k}
\end{array}
\end{align}
\]
發現四個項的值所在的區間完全錯開，這就意味著他們的二進制表示的位數范圍是完全錯開的，意味著他們的二進制運算是互不干擾的
因此原式可以轉化為：
\[\bigoplus_{i=1}^{p-1}i\times inv(i)+\bigoplus_{i=1}^{p-1}i\times2^k+\bigoplus_{i=1}^{p-1}inv(i)\times 2^{2k}+\bigoplus_{i=1}^{p-1}2^{3k}\mod{M}
\]
由于\(i\leq p,inv(i)\leq p\)且\(i\)與\(inv(i)\)一一對應，所以\(inv(i)\)為\(1\sim p-1\)的排列
則有\(\bigoplus_{i=1}^{p-1}i=\bigoplus_{i=1}^{p-1}inv(i)\)
對于\(\bigoplus_{i=1}^{p-1}i\times inv(i)\)：
- 由于\(i\times inv(i)\equiv 1\mod{p}\)，則\(inv(1)=1,inv(p-1)=p-1\)
- 對于\([a\times inv(a)]\oplus[b\times inv(b)]\)，若\(b=inv(a)\)，則\(a\times inv(a)=inv(b)\times inv(inv(b))=inv(b)\times b\)，則\([a\times inv(a)]\oplus[b\times inv(b)]=0\)
- 在\(1\sim p\)中，除了\(1,p-1\)以外，剩下的都可以\(a=inv(b)\)一一配對消去
- 因此\(\bigoplus_{i=1}^{p-1}i\times inv(i)=1\oplus(p-1)^2\)
- 為素數，\(p-1\)則必為偶數，\((p-1)^2\)必為偶數，與1異或后不變
- 因此\(\bigoplus_{i=1}^{p-1}i\times inv(i)=(p-1)^2\)
對于\(\bigoplus_{i=1}^{p-1}i\times2^k\)：
- 由于與2的冪次做乘法就相當于右移，所以\(\bigoplus_{i=1}^{p-1}i\times2^k=2^k\times\bigoplus_{i=1}^{p-1}i\)
- 對于\(\oplus_{i=1}^{p-1}i\)，發現\(i\oplus i+1\oplus i+2\oplus i+3=0\)，記\(c=(p-1)\%4\)，則原式等于序列最后\(c\)項的異或和
- 將最后\(c\)項的異或和記為\(S\)，則\(\bigoplus_{i=1}^{p-1}i\times2^k=2^k\times S\)
對于\(\bigoplus_{i=1}^{p-1}inv(i)\times 2^{2k}\)：
- 同理等于\(2^{2k}\times \oplus_{i=1}^{p-1}inv(i)\)
- 由\(\bigoplus_{i=1}^{p-1}i=\bigoplus_{i=1}^{p-1}inv(i)\)，原式等于\(2^{2k}\times \oplus_{i=1}^{p-1}i=2^{2k}\times S\)
對于\(\bigoplus_{i=1}^{p-1}2^{3k}\)：
- \(p\)為素數，則\(p-1\)必為偶數，\(\bigoplus_{i=1}^{p-1}2^{3k}=2^{3k}\times\oplus_{i=1}^{p-1}1=0\)
則題干要求的原式可以化為：
\[(p-1)^2+(2^k+2^{2k})\times S\mod{M}
\]
計算時要注意減法取模前要加模數\(M\)
當\(k<23\)時，暴力計算即可
但是需要注意，異或運算不可以一邊取模一邊算，所以再算完異或和之后再取模
代碼實現
#include<iostream>
#include<vector>
#include<map>
#include<cmath>
#include<set>
#include<stack>
#include<unordered_map>
using namespace std;
using ll = long long;
using ull =unsigned long long;
#define int ull
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr int inf = 1e9 + 5;
constexpr int mod=998244353;
int p;
int qpow(int a,int b,int m){
int ans=1;a%=m;
while(b){
if(b%2){ans*=a;ans%=m;}
a*=a;a%=m;b>>=1;
}
return ans%m;
}
void eachT() {
cin>>p;
int k=(p+118)/119;
if(k<=22){
int ans=0;
rep(i,1,p-1){
ans^= (qpow(i,p-2,p)+(1ull<<k))*(i+(1ull<<2*k));
}
cout<<ans%mod<<'\n';
}else{
int cnt=(p-1)%4,s=0;
rep(i,0,cnt)s^=p-1-i;
s%=mod;
int pw2=qpow(2,k,mod);
int part1=(pw2*pw2+pw2)%mod*s%mod;
p%=mod;
int part2=(p*p%mod-2*p%mod+2+mod)%mod;
cout<<(part1+part2)%mod<<'\n';
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
ll t = 1;
cin >> t;
while (t--) {
eachT();
}
}
浙公網安備 33010602011771號