01. 數(shù)字信號(hào)處理概述
符號(hào)規(guī)定
| \(\Omega\) | 模擬角頻率 |
|---|---|
| \(\omega\) | 數(shù)字角頻率 |
| \(T\) | 采樣周期 |
| \(\Omega_{s}\) | 采樣角頻率 |
| \(\Omega_N\) | 連續(xù)信號(hào)最大角頻率 |
連續(xù)信號(hào)的采樣
對(duì)于一個(gè)連續(xù)信號(hào)\(x_{c}(t)\),其經(jīng)過(guò)沖擊采樣之后獲得之后變成一個(gè)沖擊串函數(shù)\(x_{s}(t)\),即:
顯然,對(duì)于\(x_{s}(t)\)任然是一個(gè)連續(xù)信號(hào),我們需要經(jīng)過(guò)量化之后獲得我們所需要的離散信號(hào)\(x[n]\),有\(x[n] = x_{c}{nT}\)
流程如圖:
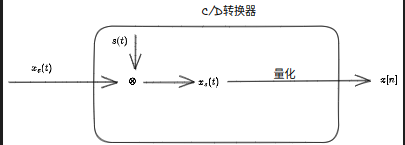
頻域分析
對(duì)\(x_{s}(t)\)進(jìn)行連續(xù)傅里葉變換有:
其中
所以有:
顯然,采樣后的頻域是對(duì)原本連續(xù)信號(hào)頻域的周期延拓,這里面要求有:
這里\(\Omega_{N}\)稱(chēng)之為奈奎斯特頻率,\(2\Omega_{N}\)稱(chēng)之為奈奎斯特率
在對(duì)\(x[n]\)進(jìn)行DTFT,有:
對(duì)比上述式子,有:
所以上面沖擊串函數(shù)的在數(shù)字頻域上可以表示:
即對(duì)采樣之后在數(shù)字角頻域進(jìn)行了歸一化
例1
假設(shè)\(T=1/600\),模擬連續(xù)信號(hào)\(x_{c}(t) = cos400\pi t\)
可以計(jì)算出:\(\Omega_{s}=1200\pi, \Omega_{N} = 800\pi\)
由時(shí)域采樣定理知:可以用一組離散信號(hào)表示原連續(xù)信號(hào)
此時(shí)\(X_{s}(j\Omega)\)圖像如下:
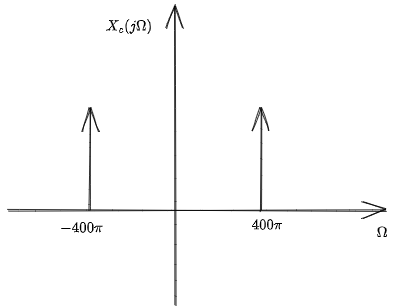
在進(jìn)行歸一化有:
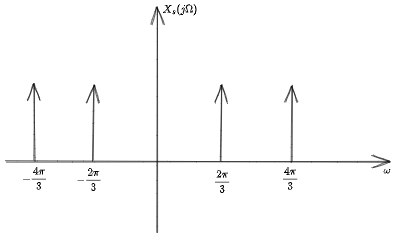
連續(xù)信號(hào)的復(fù)原
對(duì)于數(shù)字序列\(x[n]\),我們可以構(gòu)造一個(gè)連續(xù)的沖擊串函數(shù)\(x_{s}{t}\),有:
對(duì)于這個(gè)函數(shù),我們已知其在頻域上等于原連續(xù)信號(hào)的周期延拓,所以我們希望使用一個(gè)低通濾波器對(duì)其進(jìn)行濾波再添加一個(gè)T倍的增益,該門(mén)函數(shù)的截止頻率一般取\(\Omega_N\)的一般。
對(duì)于截止頻率為\(\Omega_{H}\),頻率增益為A的門(mén)函數(shù),其時(shí)域形式為:
所以有:
所以在頻域上將\(X_{s}(j\Omega)與H(j\Omega)\)相乘,在時(shí)域上表現(xiàn)為卷積,有:
則可以抽象成一個(gè)D/C轉(zhuǎn)換器
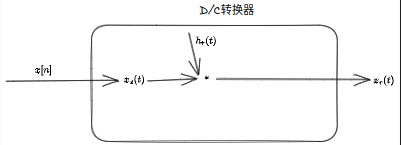
完整的步驟
時(shí)域連續(xù)信號(hào)在進(jìn)過(guò)采樣之后變成數(shù)字序列,而DSP處理的對(duì)象即為數(shù)字序列,經(jīng)過(guò)輸入到系統(tǒng)中后輸入一個(gè)響應(yīng),將輸出響應(yīng)再進(jìn)行復(fù)原成時(shí)域連續(xù)信號(hào)。
后面我們將圍繞中間系統(tǒng)部分詳細(xì)展開(kāi)。



 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)