時域采樣定理
對于一個信號，我們想對其進行采樣轉化成數字信號，顯然，當我們采樣頻率越改，我們所能保留的信息越多，但是當高采樣頻率對我們的采樣設備要求也高，我們希望找到采樣頻率和模擬信號頻率之間的一些關系
有模擬信號\(x_{a}(t)\)，我們對其進行理想采樣，即采樣信號\(\hat{x}_{a}{(t) =}x_{a}(t)\sum\limits \delta(t-nT)\)
兩邊同時進行傅里葉變換有：
\[\hat{X}_{a}(\omega) = \frac{1}{2\pi}[ X(\omega)* \Delta(\omega) ]
\]
其中\(\Delta (\omega)\)是周期函數\(\delta_{t}(t)\)的傅里葉變換
對于周期函數\(\delta_{T}(t)\)，有傅里葉級數：
\[\delta_{T}(t) = \sum\limits_{n=-\infty }^{\infty} c_{n}e^{jn\Omega_{s}t}
\]
\(\Omega_{s}\)是采樣角頻率，其中的\(c_{n}\)有：
\[\begin{aligned}
c_{n} &= \frac{1}{T}\int_{-\frac{T}{2} }^ {\frac{T}{2}}\delta_{T}(t)e^{-j\Omega_{s}t}dt\\
&=\frac{1}{T}
\end{aligned}
\]
帶入上式有：
\[\Delta(w) = \mathcal{F}\left[\frac{1}{T}\sum\limits_{n=-\infty}^{\infty}e^{jn\Omega_{s}t}\right]= \frac{1}{T}\sum\limits_{k=-\infty}^{\infty}2\pi \delta(\omega-k\Omega_{s} )
\]
再帶入上式進行卷積運算有：
\[\hat{X}_{a}(\omega) = \frac{1}{T}\sum\limits_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}X_{a}(j\theta)\cdot \delta(j(\omega - \Omega_s)-j\theta)d\theta = \frac{1}{T}\sum\limits_{k=-\infty}^{\infty}X_{a}(j\omega - jk\Omega_{s})
\]
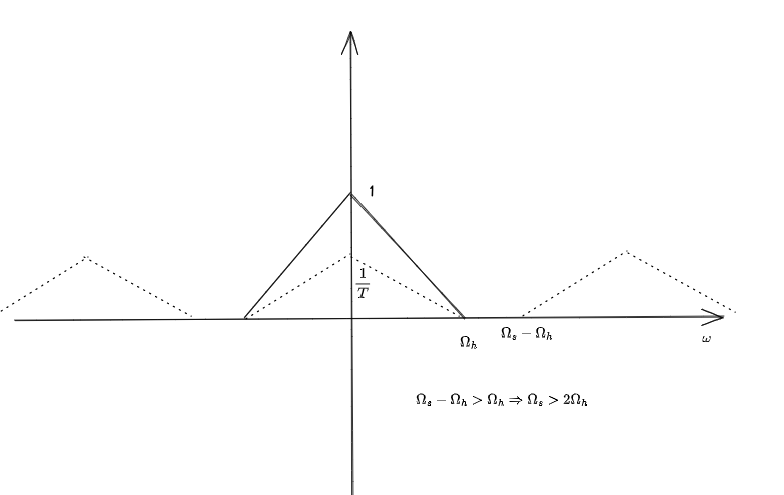
可以看到，在采樣周期為T的情況下，采樣頻率是原頻率的一個周期延拓。
可以假設如圖，原序列最高頻率為 \(\Omega_h\)，則要想周期延拓后頻率不發生交集，則必須有：
\[\Omega_{s}>2\Omega_h
\]
或者：
\[2f_{s}<f_{h}
\]
至于復原，可以乘以一個適當的傅域“禮帽序列”
浙公網安備 33010602011771號