一、 復變函數的基本知識

由于在實數域中無法表示負數開根號問題，故將數系進行擴充，定義有\(i^{2}=-1\)

1. 復數的表示法

其四則運算略

2. 幅角求解

對于\(z = x + iy\)，其幅角主值（即\((-\pi, \pi]\)部分）有：

上述公式其實很容易證明，可以現場推導，不需要死記。
畫個圖示意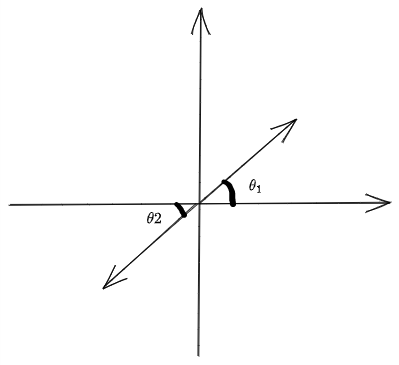

對于幅角主值，就是從\(-\pi\)轉到\(\pi\)的范圍，并且逆時針為正，顯然，對于 x>0 的時候，這個角度就等于y/x的反正切，對于 x < 0 ，以2舉例，其反正切等于1， 如果我們要由1 得到 2， 那么 1 就應該旋轉某個角度， 如果是逆時針，則角度就會超過 \(\pi\)，所以只能是順指針，即減去\(\pi\)

3. 復變函數

定義在復數域上，將一個復數映射成另一個復數。下面是一些基礎知識，建議去找專門的書籍查看詳細定義。

1. 極限

和實變函數一致，簡單點說就是從任意一個方向趨向于某個數，函數都等于同一個值；復雜點說就是 \(\epsilon - \delta\) 定義

2. 連續

如果函數在任意一點極限存在且等于函數值，怎稱其連續

3. 導數

和實變函數一樣，在某點的導數等于在該點處產生無窮小的變化時函數變化率的極限，如果該極限存在，則函數在該點可導，并且對于一般函數，其求導公式與實變函數一致

4. 解析

函數在某點的一個鄰域內處處可導，則稱函數在該點解析
如果在一個區域內處處解析，則稱在該區域解析，該函數則稱之為在該區域內的解析函數或者全純函數

5. C-R條件

4. 點、區域可導、解析的關系

如圖

5. 調和函數

定義拉普拉斯算子 $$\Delta = \frac{\partial^{2}}{x{2}} + \frac{\partial^{2}}{y{2}} $$
如果一個函數f，滿足\(f\cdot \Delta=0\) ，則稱其為調和函數
如果一個函數解析，則其實部和虛部函數都為調和函數，反之不一定，但是加上C-R條件則成立

二、復變函數的積分

1. 定義

略，簡單點說就是沿某條路徑上的第二型曲線積分

2. 計算方法

和二元第二型曲線積分類似，在復平面上，如果有參數方程

則 \(dz = df + i dg\) ， 帶入原積分，轉換成定積分
常用公式

其中 \(z_{0}\)是該閉合曲線中唯一的不解析點

3. 柯西古薩定理

在一個區域內（單聯通和復聯通都成立，方向正確即可），在其中處處解析，則在該區域中的閉合曲線上的積分為0

4. 柯西積分公式

有：

高階導數公式

三、復數項級數

1. 復數項級數的基本概念

定義 \(c_{n} = a_{n}+ib_{n}\)為復數項級數，其中的兩個為實數項級數

1. 收斂性判斷

\(c_{n}\)收斂的充要條件是\(a_{n},b_{n}\)收斂，則轉化成了判斷實數項級數
大概回顧一下實數項級數的判斷方法（懷念我的高數老師，hh）
首先有絕對收斂必收斂的概念，并且有必要條件\(\lim_{n\to\infty}a_{n} = 0\)

1. 比較法和極限比較法 --> 對于兩個正項數列，較大的收斂，較小的也收斂，較小的發散，較大的一定發散
2. 根值法 --> \(lim_{n\to\infty} a_{n}^{\frac{1}{n}} = \lambda\) ，當\(\lambda <1\) 收斂
3. 比值法 --> 類似于根值法
   上面三種是正項級數的常用判別法，一般都是利用絕對收斂再加上上述方法，并且常用比較對象是p級數和等比級數

對于交錯級數 ：絕對值單調遞減并且極限為0則收斂

同理、復數項級數也滿足絕對收斂

2. 冪級數

1. 收斂半徑

即滿足

2. 阿貝爾定理

如果冪級數在\(z_0\)處收斂，在\(|z|<|z_{0}|\)內絕對收斂，由此可通過收斂半徑得到收斂域

3. 泰勒展開

和實函數一致，并且常用的展開也一致

4. 洛朗展開

泰勒展開的推廣，一般還是改變形式轉化成常用泰勒展開的范圍去展開

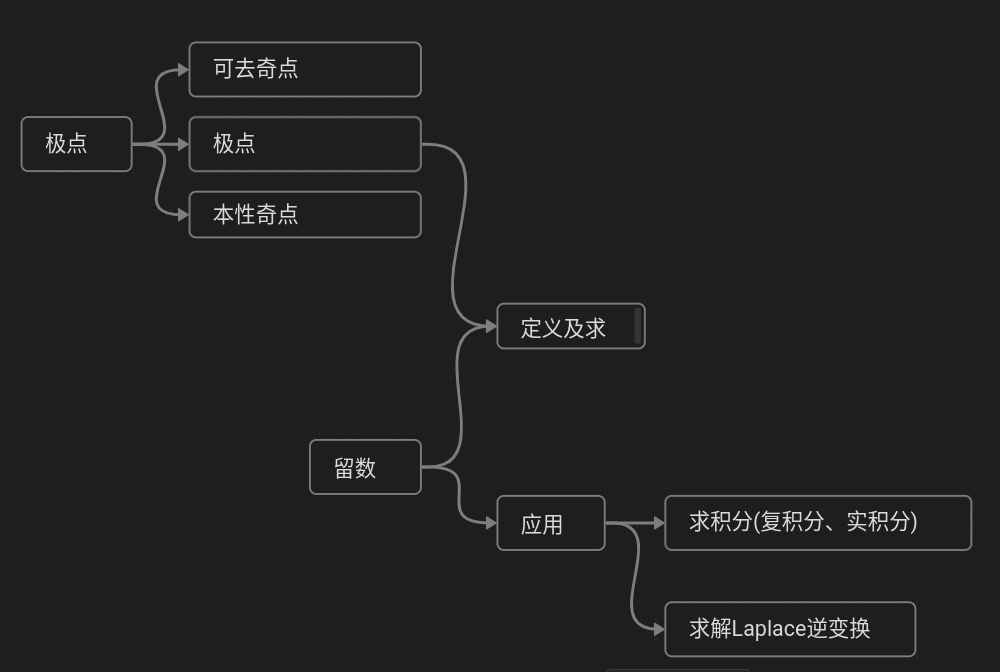
四、留數及其應用

定義留數等于洛朗展開 負一次冪的系數
后面累了，不想搞了QAQ