一致性模型（consistency model）是擴(kuò)散模型（Diffusion Models）的圖像生成加速方法，通過將隨機(jī)過程轉(zhuǎn)化為常微分方程（ODE），引入Consistency Regularization實(shí)現(xiàn)一步或少數(shù)幾步生成。LCM/LCM-Lora進(jìn)一步通過Skipping-Step和Classifier-free guidance（CFG）優(yōu)化，代碼可參考diffusers庫實(shí)踐。

前面已經(jīng)介紹了擴(kuò)散模型，在最后的結(jié)論里面提到一點(diǎn)：擴(kuò)散模型往往需要多步才能生成較為滿意的圖像。不過現(xiàn)在有一種新的方式來加速（旨在通過少數(shù)迭代步驟）生成圖像：一致性模型（consistency model），因此這里主要是介紹一致性模型（consistency model）基本原理以及代碼實(shí)踐，值得注意的是本文不會(huì)過多解釋數(shù)學(xué)原理，數(shù)學(xué)原理推導(dǎo)可以參考：

具體代碼推導(dǎo)可以直接看最后對(duì)于LCM代碼分析。介紹一致性模型之前需要了解幾個(gè)知識(shí)：在傳統(tǒng)的擴(kuò)散模型中無論是加噪還是解噪過程都是隨機(jī)的，在論文^[1]中（也就是CM作者宋博士的另外一篇論文）將這個(gè)隨機(jī)過程（也就是隨機(jī)微分方程SDE）轉(zhuǎn)化成“固定的”過程（也就是常微分方程ODE），只有過程可控才能保證下面公式成立。

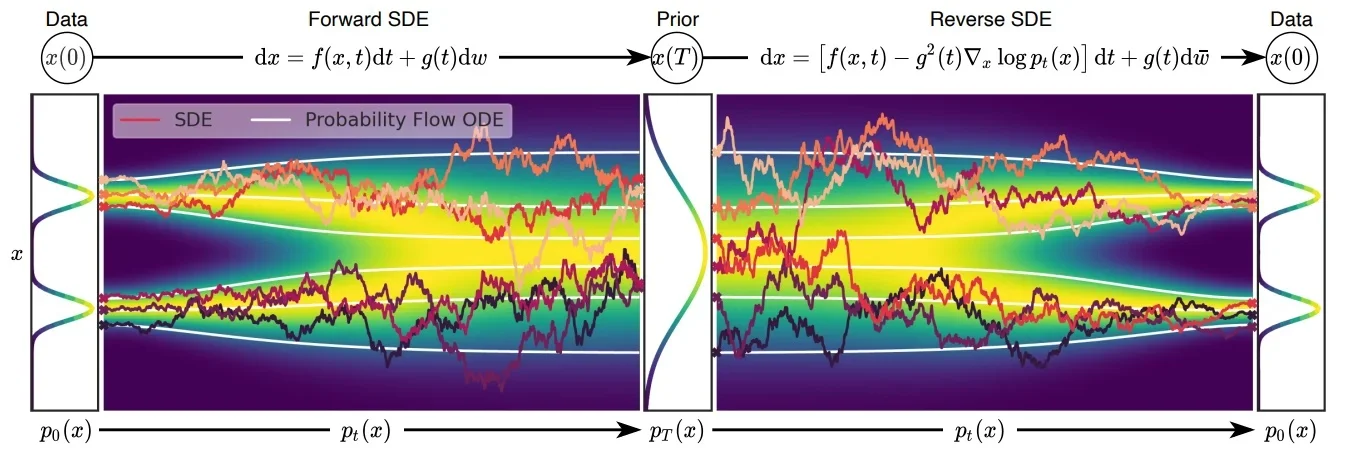
一致性模型（Consistency Model）

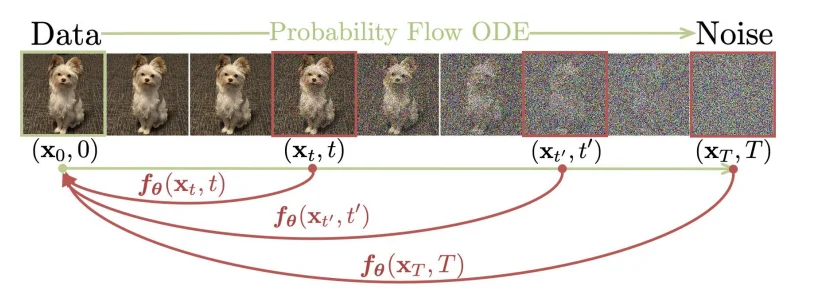
其中ODE（常微分方程），在傳統(tǒng)的擴(kuò)散模型（Diffusion Models, DM）中，前向過程是從原始圖像 \(x_0\)開始，不斷添加噪聲，經(jīng)過 \(T\)步得到高斯噪聲圖像 \(x_T\)。反向過程（如 DDPM）通常通過訓(xùn)練一個(gè)逐步去噪的模型，將 \(x_T\)逐步還原為 \(x_0\) ，每一步估計(jì)一個(gè)中間狀態(tài)，因此推理成本高（需迭代 T 步）。而在 Consistency Models（CM） 中，模型訓(xùn)練時(shí)引入了 Consistency Regularization，使得模型在不同的時(shí)間步 \(t\)都能一致地預(yù)測(cè)干凈圖像。這樣在推理時(shí)，無需迭代多步，而是可以通過一個(gè)單一函數(shù)\(f(x ,t)\) 直接將任意噪聲圖像\(x_t\) 還原為目標(biāo)圖像\(x_0\) 。這大大減少了推理時(shí)間，實(shí)現(xiàn)了一步（或少數(shù)幾步）生成。

一致性模型（consistency model）在論文^[2]里面主要是通過使用常微分方程角度出發(fā)進(jìn)行解釋的。Consistency Model 在 Diffusion Model 的基礎(chǔ)上，新增了一個(gè)約束：從某個(gè)樣本到某個(gè)噪聲的加噪軌跡上的每一個(gè)點(diǎn)，都可以經(jīng)過一個(gè)函數(shù) \(f\) 映射為這條軌跡的起點(diǎn)（也就是通過擴(kuò)散處理的圖像在不同的時(shí)間 \(t\) 都可以直接轉(zhuǎn)化為最開始的圖像 \(x_0\)），用數(shù)學(xué)描述就是：\(f:(x_t, t)\rightarrow x_\epsilon\)，換言之就是需要滿足： \(f(x_t,t)=f(x_{t^\prime},t^\prime)\) 其中 \(t,t^\prime \in [\epsilon,T]\)，正如論文里面的圖片描述：

要滿足上面的計(jì)算關(guān)系，作者在論文里面定義如下的等式關(guān)系（下面等式關(guān)系就是CM中核心概念）：

其中等式需要滿足：\(c_{skip}(\epsilon)=1,c_{out}(\epsilon)=0\) （\(c_{skip}(t)=\frac{\sigma_{data}^2}{(t- \epsilon)^2+ \sigma_{data}^2}\)， \(c_{out}(t)=\frac{\sigma_{data}(t-\epsilon)}{\sqrt{\sigma_{data}^2+ t^2}}\)），隨著解噪過程（時(shí)間從：\(T \rightarrow \epsilon\) 其中 \(c_{skip}\) 的值逐漸增大，也就是當(dāng)前的解噪圖像占比權(quán)重增加），其中我的 \(F_\theta\) 就是我們的神經(jīng)網(wǎng)絡(luò)模型（比如Unet）。既然使用了神經(jīng)網(wǎng)絡(luò)那么必定就需要設(shè)計(jì)一個(gè)損失函數(shù)，在論文里面作者設(shè)計(jì)的損失函數(shù)為：兩個(gè)時(shí)間步之間生成得到的圖像距離通過最小化這個(gè)值（比如說 \(\Vert x_{t+1} - x_t \Vert_2\)）來優(yōu)化模型參數(shù)。作者對(duì)于模型訓(xùn)練給出兩種訓(xùn)練方式

直接通過蒸餾模型進(jìn)行優(yōu)化

通過直接蒸餾的方式對(duì)模型參數(shù)進(jìn)行優(yōu)化，其中設(shè)計(jì)的損失函數(shù)為：

其中 \(d\)代表距離（比如 \(l_1\) 或者 \(l_2\) ）對(duì)于上面公式代表的含義是：從樣本集中得到一個(gè)樣本，而后加噪得到 \(x_{t_{n+1}}\) ，然后利用預(yù)訓(xùn)練的 Diffusion 模型去一次噪，預(yù)測(cè)到另外一個(gè)點(diǎn) \(\hat{x}_{t_n}^{\phi}\) 然后計(jì)算這兩個(gè)點(diǎn)送入后的結(jié)果，用特定損失函數(shù)約束其一致（也就是： 模型在兩個(gè)時(shí)間步之間的預(yù)測(cè)結(jié)果是否一致 也就是 \(f_\theta(t_{n+k})=f_\theta(t_n)\)，其他的DF模型一般學(xué)的是噪聲是不是一致的）。其中預(yù)測(cè)過程就是使用ODE solver進(jìn)行處理，比如說：

其中DDIM、DPM++就是ODE solver一種。

歐拉法： \(y_{n+1}= y_n+h*f(t_n, y_n)\) 其中h代表時(shí)間步長(zhǎng)，f代表當(dāng)前導(dǎo)數(shù)估計(jì)。不過值得進(jìn)一步了解的是，在DL中大部分函數(shù)都是直接通過神經(jīng)網(wǎng)絡(luò)進(jìn)行“估算的”，也就是說對(duì)于上面的 \(\nabla_{x_{t_{n+1}}}\log p_{t_{n+1}} \textcolor{red}{≈} s_\theta(x_{t_{n+1}},t_{n+1})\) 其中 \(s_\theta\)代表的是訓(xùn)練好的去噪網(wǎng)絡(luò)。

那么這樣一來整個(gè)過程就變成了：

直接訓(xùn)練模型進(jìn)行優(yōu)化

直接訓(xùn)練模型進(jìn)行優(yōu)化，其中具體的過程為：

LCM/LCM-Lora

潛在一致性模型（Latent Consistency Model）^[3]以及LCM-Lora^[4]（LCM的Lora優(yōu)微調(diào)）通過再latent space中使用一致性模型（stable diffusion model通過VAE將圖像進(jìn)行壓縮到latent sapce而后通過DF模型訓(xùn)練并且最后再通過VAE decoder輸出），在LCM中主要提出兩點(diǎn)：
1、Skipping-Step：因?yàn)樵谧铋_始的CM中計(jì)算兩個(gè)相鄰的時(shí)間步之間的loss由于時(shí)間步過于接近，就會(huì)導(dǎo)致loss很小，因此通過跳步解決這個(gè)問題，這樣loss就會(huì)變成：\(d(f(x_{t_{n+\textcolor{red}{k}}}, t_{n+\textcolor{red}{k}}), f(x_{t_n}, t_n))\)。
2、引入Classifier-free guidance (CFG) 那么整個(gè)loss計(jì)算就會(huì)變成：\(d(f(x_{t_{n+\textcolor{red}{k}}}, \textcolor{red}{w}+ \textcolor{red}{c}, t_{n+\textcolor{red}{k}}), f(x_{t_n}, \textcolor{red}{w}+ \textcolor{red}{c}+ t_n))\)，公式中c代表文本，對(duì)于CFG而言其實(shí)就是一個(gè)改進(jìn)的ODE solver（見下面算法流程中的藍(lán)色部分）

對(duì)于LCD算法流程，其中藍(lán)色部分為L(zhǎng)CM所修改的內(nèi)容：

對(duì)于最后得到的實(shí)驗(yàn)結(jié)果分析：

• 不同的k對(duì)結(jié)果的影響

在DPM-solver++和DPM-Solver中基本只需要 2000 步迭代，LCM 4 步采樣的 FID 就已經(jīng)基本收斂了

• 不同的Guidance Scale對(duì)結(jié)果的影響

LCM 作者用不同 LCM 的迭代次數(shù)與不同 Guidance Scale 做了對(duì)比。發(fā)現(xiàn) \(w\) 增加有助于提升 CLIP Score，但是損失了 FID 指標(biāo)（即多樣性）的表現(xiàn)。另外，LCM 迭代次數(shù)為 2、4、8 時(shí)，CLIP Score 和 FID 相差都不大，說明了 LCM 的蒸餾性能確實(shí)非常強(qiáng)悍，兩步前向的效果可能都足夠好了，只是一步前向的結(jié)果還差些。
總得來說，在LCM中主要是做了如下幾點(diǎn)改進(jìn)：1、使用skipping-step來“拉大”相鄰點(diǎn)之間的距離計(jì)算；2、改進(jìn)了ODE solver。

LCM蒸餾訓(xùn)練到底在做什么？

通過結(jié)合代碼理解

首先直接使用我們使用我們訓(xùn)練好的unet模型（unet = UNet2DConditionModel.from_pretrained）作為函數(shù)\(f_\theta\)。因?yàn)樵贑M中基于ODE（常微分方程）保證“路徑”一致，并且CM核心觀點(diǎn)就是希望模型學(xué)習(xí)從一個(gè)“晚”的時(shí)間步（接近噪聲狀態(tài)）預(yù)測(cè)出一個(gè)“早”的時(shí)間步（接近干凈圖像）下的表示（讓模型學(xué)習(xí) \(z_{t_{n+k}}\) 預(yù)測(cè)出 \(z_{t_n}\)）。那么代碼處理方式就是：

bsz = latents.shape[0]
topk = noise_scheduler.config.num_train_timesteps // args.num_ddim_timesteps #noise_scheduler使用的DDPM topk=1000//50
index = torch.randint(0, args.num_ddim_timesteps, (bsz,), device=latents.device).long()
# 得到 t_{n+k}
start_timesteps = solver.ddim_timesteps[index]
# 得到 t_{n}
timesteps = start_timesteps - topk #solver使用的DDIM
timesteps = torch.where(timesteps < 0, torch.zeros_like(timesteps), timesteps)
c_skip_start, c_out_start = scalings_for_boundary_conditions(start_timesteps,...)
...
c_skip, c_out = scalings_for_boundary_conditions(timesteps, ...)
...
noisy_model_input = noise_scheduler.add_noise(latents, noise, start_timesteps)

而后在得到噪聲之后直接輸入到模型中也就是計(jì)算預(yù)測(cè)噪聲（noise_pred = unet(noisy_model_input,...).sample）并且去反推預(yù)測(cè)結(jié)果 \(F_\theta(x,t)\)（pred_x_0 = get_predicted_original_sample()）然后再去根據(jù)最上面公式（\(f_\theta(x,t)=c_{skip}(t)x+ c_{out}(t)F_\theta(x,t)\)）就可以得到（學(xué)生模型）最后的輸出model_pred=c_skip_start * noisy_model_input + c_out_start * pred_x_0（也就對(duì)應(yīng)上：從某個(gè)樣本到某個(gè)噪聲的加噪軌跡上的每一個(gè)點(diǎn)，都可以經(jīng)過一個(gè)函數(shù)映射為這條軌跡的起點(diǎn) ）。也就對(duì)應(yīng)下面代碼：

noisy_model_input = noise_scheduler.add_noise(latents, noise, start_timesteps)
...
noise_pred = unet(noisy_model_input,...).sample
pred_x_0 = get_predicted_original_sample(noise_pred,start_timesteps,noisy_model_input,noise_scheduler.config.prediction_type...)#計(jì)算反推樣本起點(diǎn)x0
model_pred = c_skip_start * noisy_model_input + c_out_start * pred_x_0

然后就是需要去計(jì)算教師模型的輸出，處理過程和上面的處理方式是相似的（讓模型學(xué)習(xí) \(z_{t_{n+k}}\) 預(yù)測(cè)出 \(z_{t_n}\)）也就是對(duì)應(yīng)下面的：

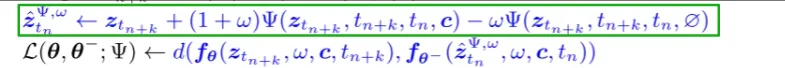
那么具體的代碼操作如下：

noisy_model_input = noise_scheduler.add_noise(latents, noise, start_timesteps)
...
accelerator.unwrap_model(unet).disable_adapters() # 因?yàn)槲矣胠ora去微調(diào)我的模型因此教師模型首先將lora取消掉
with torch.no_grad():
  # 1. Get teacher model prediction on noisy_model_input z_{t_{n + k}} and conditional embedding c
  cond_teacher_output = unet(noisy_model_input,start_timesteps,...).sample
  cond_pred_x0 = get_predicted_original_sample(cond_teacher_output,start_timesteps,noisy_model_input,...)
  cond_pred_noise = get_predicted_noise(cond_teacher_output,start_timesteps,noisy_model_input,...)

  # 2. Get teacher model prediction on noisy_model_input z_{t_{n + k}} and unconditional embedding 0
  uncond_prompt_embeds = torch.zeros_like(prompt_embeds)
  uncond_pooled_prompt_embeds = torch.zeros_like(encoded_text["text_embeds"])
  uncond_added_conditions = copy.deepcopy(encoded_text)
  uncond_added_conditions["text_embeds"] = uncond_pooled_prompt_embeds
  uncond_teacher_output = unet(noisy_model_input,start_timesteps,encoder_hidden_states=uncond_prompt_embeds.to(weight_dtype),encoder_hidden_states=uncond_prompt_embeds.to(weight_dtype),added_cond_kwargs={k: v.to(weight_dtype) for k, v in uncond_added_conditions.items()},).sample
  uncond_pred_x0 = get_predicted_original_sample(uncond_teacher_output,start_timesteps,noisy_model_input,...)
  uncond_pred_noise = get_predicted_noise(uncond_teacher_output,start_timesteps,noisy_model_input,...)

  # 3. Calculate the CFG estimate of x_0 (pred_x0) and eps_0 (pred_noise)
  pred_x0 = cond_pred_x0 + w * (cond_pred_x0 - uncond_pred_x0)
  pred_noise = cond_pred_noise + w * (cond_pred_noise - uncond_pred_noise)
  # 4. Run one step of the ODE solver to estimate the next point x_prev on the
  # augmented PF-ODE trajectory (solving backward in time)
  # Note that the DDIM step depends on both the predicted x_0 and source noise eps_0.
  x_prev = solver.ddim_step(pred_x0, pred_noise, index).to(unet.dtype)

對(duì)于上述代碼可以這么理解，因?yàn)槲业膶W(xué)生模型（已經(jīng)使用了lora進(jìn)行處理）因?yàn)樵贑M的訓(xùn)練過程中核心（核心思想是把輸入 \(x\)的一部分“直接跳過” （\(c_{skip}\)），剩下的部分用模型預(yù)測(cè) \(F_\theta\)修正）的一點(diǎn)就是計(jì)算：\(f_\theta(x,t)=c_{skip}(t)x+ c_{out}(t)F_\theta(x,t)\)，那么對(duì)應(yīng)學(xué)生和教師模型處理方式是一致的，只不過在LCM中會(huì)使用CFG所以處理過程就比學(xué)生模型稍復(fù)雜一點(diǎn)，不過值得注意的一點(diǎn)的是在教師模型里面會(huì)使用 x_prev = solver.ddim_step(pred_x0, pred_noise, index).to(unet.dtype)讓 教師模型為學(xué)生模型提供一條確定的去噪路徑（這個(gè)過程直接通過ODE計(jì)算得到），從而讓學(xué)生模型學(xué)習(xí)如何從噪聲生成高質(zhì)量樣本，而后就是計(jì)算loss：

start_timesteps = solver.ddim_timesteps[index]
timesteps = start_timesteps - topk
...
accelerator.unwrap_model(unet).enable_adapters()
with torch.no_grad():
  target_noise_pred = unet(x_prev,timesteps,...).sample
  pred_x_0 = get_predicted_original_sample(target_noise_pred,timesteps,x_prev,)
  target = c_skip * x_prev + c_out * pred_x_0

if args.loss_type == "l2":
  loss = F.mse_loss(model_pred.float(), target.float(), reduction="mean")

通過上面一系列處理之后得到：學(xué)生模型預(yù)測(cè)得到的：model_pred，教師模型指的道路：x_prev。因?yàn)長(zhǎng)CM要實(shí)現(xiàn)跳步處理計(jì)算loss：\(\mathcal{L}=\left\|f_\phi(x_{t_s},t_s)-\mathrm{sg}[f_\theta(x_{t_e},t_e)]\right\|^2\)。

總結(jié)

總的來說consistency model作為一種diffusion model生成（區(qū)別與DDPM/DDIM）加速操作，在理論上首先將隨機(jī)生成過程變成“確定”過程，這樣一來生成就是確定的，從 \(T\rightarrow t_0\) 所有的點(diǎn)都在“一條線”上等式 \(f(x_t,t)=f(x_{t^\prime},t^\prime)\) 其中 \(t,t^\prime \in [\epsilon,T]\) 成立那么就保證了模型不需要再去不斷依靠 \(t+1\) 生成內(nèi)容去推斷 \(t\)時(shí)刻內(nèi)容（具體可以參考算法流程圖）。而后續(xù)的LCM/LCM-Lora/TCD^[5]則是基于CM的原理進(jìn)行改進(jìn)。

參考

---

1. https://arxiv.org/pdf/2011.13456 ??

2. https://arxiv.org/abs/2303.01469 ??

3. https://arxiv.org/abs/2310.04378 ??

4. https://arxiv.org/abs/2311.05556 ??

5. https://arxiv.org/abs/2402.19159 ??