更加好的排版：https://www.big-yellow-j.top/posts/2025/05/19/DiffusionModel.html
前文已經(jīng)介紹了VAE以及GAN這里介紹另外一個(gè)模型：Diffusion Model，除此之外介紹Conditional diffusion model、Latent diffusion model

Diffusion Model

diffusion model（后續(xù)簡(jiǎn)稱(chēng)df）模型原理很簡(jiǎn)單：前向過(guò)程在一張圖像基礎(chǔ)上不斷添加噪聲得到一張新的圖片之后，反向過(guò)程從這張被添加了很多噪聲的圖像中將其還原出來(lái)。原理很簡(jiǎn)單，下面直接介紹其數(shù)學(xué)原理：

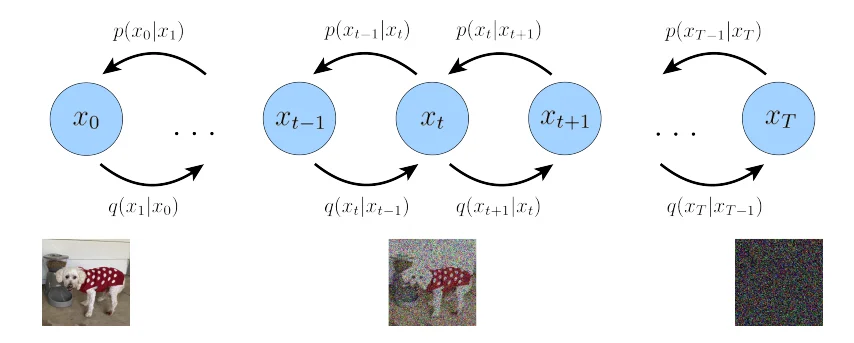
上圖中實(shí)線代表：反向過(guò)程（去噪）；虛線代表：前向過(guò)程（加噪）

那么我們假設(shè)最開(kāi)始的圖像為 \(x_0\)通過(guò)不斷添加噪聲（添加噪聲過(guò)程假設(shè)為\(t\)）那么我們的 前向過(guò)程：\(q(x_1,...,x_T\vert x_0)=q(x_0)\prod_{t=1}^T q(x_t\vert x_{t-1})\)，同理 反向過(guò)程：\(p_\theta(x_0,...\vert x_{T})=p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}\vert x_t)\)

前向過(guò)程

在df的前向過(guò)程中：

通常定義如下的高斯分布：\(q(x_t\vert x_{t-1})=N(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_tI)\)，其中參數(shù)\(\beta\)就是我們的 噪聲調(diào)度參數(shù)來(lái)控制我們每一步所添加的噪聲的“權(quán)重”（這個(gè)權(quán)重可以固定也可以時(shí)間依賴(lài)，對(duì)于時(shí)間依賴(lài)很好理解最開(kāi)始圖像是“清晰”的在不斷加噪聲過(guò)程中圖像變得越來(lái)越模糊），于此同時(shí)隨著不斷的添加噪聲那么數(shù)據(jù)\(x_0\)就會(huì)逐漸的接近標(biāo)準(zhǔn)正態(tài)分布 \(N(0,I)\)的 \(x_t\)，整個(gè)加噪過(guò)程就為：

在上述過(guò)程中我們可以將\(t=1\)得到的 \(x_1\)代到下面 \(t=2\)的公式中，類(lèi)似的我們就可以得到下面的結(jié)果：\(x_2=\sqrt{(1-\beta_2)(1-\beta_1)}x_0+ \sqrt{1-(1-\beta_2)(1-\beta_1)}\epsilon\) （之所以用一個(gè)\(\epsilon\)是因?yàn)樯厦鎯蓚€(gè)都是服從相同高斯分布就可以直接等同過(guò)來(lái)）那么依次類(lèi)推就可以得到下面結(jié)果：

其中：\(\bar{\alpha_T}=\sqrt{(1-\beta_1)\dots(1-\beta_T)}\)，那么也就是說(shuō)對(duì)于前向過(guò)程（加噪過(guò)程）可以從\(x_0\)到 \(x_T\)一步到位，不需要說(shuō)再去逐步計(jì)算中間狀態(tài)了。

反向過(guò)程

反向過(guò)程：\(p_\theta(x_0,...\vert x_{T})=p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}\vert x_t)\)，也就是從最開(kāi)始的標(biāo)準(zhǔn)正態(tài)分布的 \(x_t\)逐步去除噪聲最后還原得到 \(x_0\)。仔細(xì)閱讀上面提到的前向和反向過(guò)程中都是條件概率但是在反向傳播過(guò)程中會(huì)使用一個(gè)參數(shù)\(\theta\)，這是因?yàn)榍跋蜻^(guò)程最開(kāi)始的圖像和噪聲我們是都知道的，而反向過(guò)程比如\(p(x_{t-1}\vert x_t)\)是難以直接計(jì)算的，需要知道整個(gè)數(shù)據(jù)分布，因此我們可以通過(guò)神經(jīng)網(wǎng)路去近似這個(gè)分布，而這個(gè)神經(jīng)網(wǎng)絡(luò)就是我們的參數(shù)：\(\theta\)。于此同時(shí)反向過(guò)程也會(huì)建模為正態(tài)分布：\(p_\theta(x_{t-1}\vert x_t)=N(x_{t-1};\mu_\theta(x_t,t),\sum_\theta(x_t,t))\)，其中 \(\sum_\theta(x_t,t)\)為我們的方差對(duì)于在值可以固定也可以采用網(wǎng)絡(luò)預(yù)測(cè)^[1]

在OpenAI的Improved DDPM中使用的就是使用預(yù)測(cè)的方法：\(\sum_\theta(x_t,t)=\exp(v\log\beta_t+(1-v)\hat{\beta_t})\)，直接去預(yù)測(cè)系數(shù)：\(v\)

回顧一下生成模型都在做什么。在GAN中是通過(guò) 生成器網(wǎng)絡(luò) 來(lái)擬合正式的數(shù)據(jù)分布也就是是 \(G_\theta(x)≈P(x)\)，在 VAE中則是通過(guò)將原始的數(shù)據(jù)分布通過(guò)一個(gè) 低緯的潛在空間來(lái)表示其優(yōu)化的目標(biāo)也就是讓 \(p_\theta(x)≈p(x)\)，而在Diffusion Model中則是直接通過(guò)讓我們 去噪過(guò)程得到結(jié)果 和 加噪過(guò)程結(jié)果接近，什么意思呢？df就像是一個(gè)無(wú)監(jiān)督學(xué)習(xí)我所有的GT都是知道的（每一步結(jié)果我都知道）也就是是讓?zhuān)?span id="w0obha2h00" class="math inline">\(p_\theta(x_{t-1}\vert x_t)≈p(x_{t-1}\vert x_t)\) 換句話說(shuō)就是讓我們最后解碼得到的數(shù)據(jù)分布和正式的數(shù)據(jù)分布相似：\(p_\theta(x_0)≈p(x_0)\) 既然如此知道我們需要優(yōu)化的目標(biāo)之后下一步就是直接構(gòu)建損失函數(shù)然后去優(yōu)化即可。

優(yōu)化過(guò)程

通過(guò)上面分析，發(fā)現(xiàn)df模型的優(yōu)化目標(biāo)和VAE的優(yōu)化目標(biāo)很相似，其損失函數(shù)也是相似的，首先我們的優(yōu)化目標(biāo)是最大化下面的邊際對(duì)數(shù)似然^[2]：\(\log p_\theta(x_0)=\log \int_{x_{1:T}}p_\theta(x_0,x_{1:T})dx_{1:T}\)，對(duì)于這個(gè)積分計(jì)算是比較困難的，因此引入：\(q(x_{1:T}\vert x_0)\) 那么對(duì)于這個(gè)公式有：

中間化簡(jiǎn)步驟可以見(jiàn)論文^[2:1]中的描述（論文里面有兩個(gè)推導(dǎo)，推導(dǎo)步驟直接省略，第二個(gè)等式： \(q(x_t\vert x_{t-1})=q(x_t\vert x_{t-1},x_0)\)），那么上面結(jié)果分析，在計(jì)算我們的參數(shù)\(\theta\)時(shí)候（反向傳播求導(dǎo)計(jì)算）第2項(xiàng)直接為0，第1項(xiàng)可以直接通過(guò)蒙特卡洛模擬就行計(jì)算，那么整個(gè)結(jié)果就只有第三項(xiàng)，因此對(duì)于第二個(gè)燈飾為例可以將優(yōu)化目標(biāo)變?yōu)椋?span id="w0obha2h00" class="math inline">\(\text{arg}\min_\theta D_{KL}(q(x_{t-1}\vert x_t, x_0)\Vert p_\theta(x_{t-1}\vert x_t))\)
對(duì)于這個(gè)優(yōu)化目標(biāo)根據(jù)論文^[3]可以得到：

最終，訓(xùn)練目標(biāo)是讓神經(jīng)網(wǎng)絡(luò) \(\epsilon_\theta\) 準(zhǔn)確預(yù)測(cè)前向過(guò)程中添加的噪聲，從而實(shí)現(xiàn)高效的去噪生成,因此整個(gè)DF模型訓(xùn)練和采樣過(guò)程就變?yōu)?sup class="footnote-ref">[3:1]：

比如說(shuō)下面一個(gè)例子：對(duì)于輸入數(shù)據(jù)\(x_0=[1,2]\) 于此同時(shí)假設(shè)我們的采樣噪聲 \(\epsilon \in[0.5, -0.3]\)并且進(jìn)行500次加噪聲處理，假設(shè)\(\bar{\alpha}_{500} = 0.8\)那么計(jì)算500次加噪得到結(jié)果為：

關(guān)鍵在于損失函數(shù)，通過(guò)上面簡(jiǎn)化過(guò)程可以直接通過(guò)模型預(yù)測(cè)噪聲因此可以直接計(jì)算\(\epsilon_\theta(x_t,t)=[0.48，-0.28]\)然后去計(jì)算loss即可。直接上代碼，代碼實(shí)現(xiàn)上面過(guò)程可以自定義實(shí)現(xiàn)/使用diffusers^[4]
diffusers實(shí)現(xiàn)簡(jiǎn)易demo

from diffusers import DDPMScheduler

# 直接加載訓(xùn)練好的調(diào)度器
# scheduler = DDPMScheduler.from_pretrained("google/ddpm-cat-256")
# 初始化調(diào)度器
scheduler = DDPMScheduler(num_train_timesteps=1000) #添加噪聲步數(shù)
...
for image in train_dataloader:
    # 假設(shè) image為 32，3，128，128
    noise = torch.randn(image.shape, device=image.device)
    timesteps = torch.randint(0, noise_scheduler.config.num_train_timesteps, 
                                      (image.shape[0],), device=image.device, dtype=torch.int64)
    noisy_images = scheduler.add_noise(image, noise, timesteps) # 32 3 128 128
    ...
    noise_pred = model(noisy_images)
    loss = F.mse_loss(noise_pred, noise)
    ...

Conditional Diffusion Model

條件擴(kuò)散模型（Conditional Diffusion Model）^[5]顧名思義就是在使用DF過(guò)程中添加一個(gè) 限定條件（文本、圖像等）來(lái)指導(dǎo)模型的生成（原理很簡(jiǎn)單，而且 條件擴(kuò)散模型這個(gè)概念比較廣泛，只要在生成圖片過(guò)程中加上一個(gè)“條件”），這里主要介紹OpenAI的論文來(lái)解釋 條件擴(kuò)散模型。

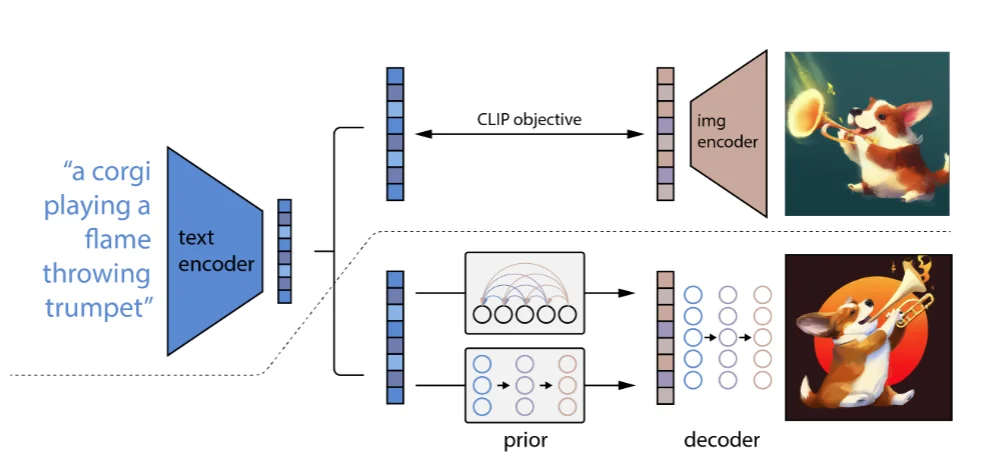
在論文里面提到了一點(diǎn)： 可以通過(guò)文本來(lái)提升模型的生成質(zhì)量。主要了解一下對(duì)于條件如何嵌入到模型中：
1、直接相加范式：這類(lèi)主要就是將文本、標(biāo)簽進(jìn)行編碼之后直接和 噪聲/ 時(shí)間步進(jìn)行相加而后進(jìn)行后續(xù)實(shí)驗(yàn)；
2、注意力融合范式：比如下面的Stable Diffusion直接將文本編碼之后融入到注意力里面進(jìn)行計(jì)算

Latent Diffusion Model

對(duì)于Latent Diffusion Model（LDM）^[6]主要出發(fā)點(diǎn)就是：最開(kāi)始的DF模型在像素空間（高緯）進(jìn)行評(píng)估這是消耗計(jì)算的，因此LDF就是直接通過(guò)對(duì) autoencoding model得到的 潛在空間（低維）進(jìn)行建模。整個(gè)思路就比較簡(jiǎn)單，用降低維度的潛在空間來(lái)進(jìn)行建模，整個(gè)模型結(jié)構(gòu)為（代碼操作）：

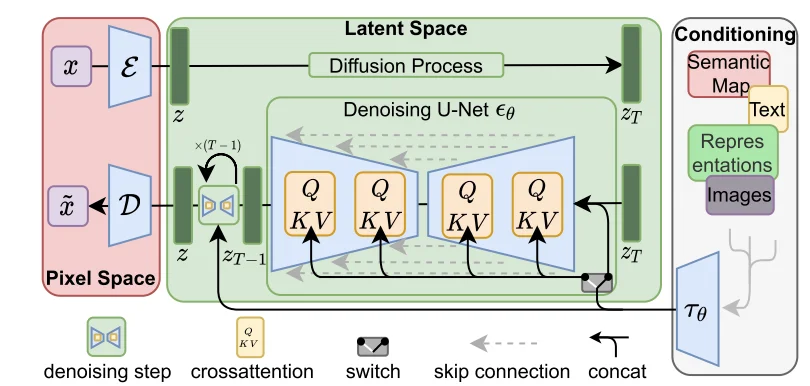
對(duì)于上述過(guò)程，輸入圖像為\(x=[3,H,W]\)而后通過(guò)encoder將其轉(zhuǎn)化為 潛在空間（\(z=\varepsilon(x)\)）而后直接在潛在空間 \(z\)進(jìn)行擴(kuò)散處理得到\(z_T\)直接對(duì)這個(gè)\(z_T\)通過(guò)U-Net進(jìn)行建模，整個(gè)過(guò)程比較簡(jiǎn)單。不過(guò)值得注意的是在U-Net里面因?yàn)榭赡軐?shí)際使用DF時(shí)候會(huì)有一些特殊輸入（文本、圖像等）因此會(huì)對(duì)這些內(nèi)容通過(guò)一個(gè)encoder進(jìn)行編碼得到：\(\tau_\theta(y)\in R^{M\times d_\tau}\)，而后直接進(jìn)行注意力計(jì)算：

其中：\(Q=W_{Q}^{(i)}\cdot\varphi_{i}(z_{t}),K=W_{K}^{(i)}\cdot\tau_{\theta}(y),V=W_{V}^{(i)}\cdot\tau_{\theta}(y)\)并且各個(gè)參數(shù)維度為：\(W_V^{i}\in R^{d\times d_\epsilon^i},W_Q^i\in R^{d\times d_\tau},W_k^i\in R^{d\times d_\tau}\)

DF模型生成

DDPM

最開(kāi)始上面有介紹如何使用DF模型來(lái)進(jìn)行生成，比如說(shuō)在DDPM中生成范式為：

也就是說(shuō)DDPM生成為：

但是這種生成范式存在問(wèn)題，比如說(shuō)T=1000那就意味著一張“合格”圖片就需要進(jìn)行1000次去噪如果1次是為為0.1s那么總共時(shí)間大概是100s如果要生產(chǎn)1000張圖片那就是：1000x1000x0.1/60≈27h。這樣時(shí)間花銷(xiāo)就會(huì)比較大

DDIM

最開(kāi)始在介紹DDPM中將圖像的采樣過(guò)程定義為馬爾科夫鏈過(guò)程，而DDIM^[7]則是相反直接定義為：非馬爾科夫鏈過(guò)程

并且定義圖像生成過(guò)程為：

代碼操作

DF模型結(jié)構(gòu)

通過(guò)上面分析，知道對(duì)于 \(x_T=\sqrt{\bar{\alpha_T}}x_0+ \sqrt{1-\bar{\alpha_T}}\epsilon\)通過(guò)這個(gè)方式添加噪聲，但是實(shí)際因?yàn)闀r(shí)間是一個(gè)標(biāo)量，就像是最開(kāi)始的位置編碼一樣，對(duì)于這些內(nèi)容都會(huì)通過(guò)“類(lèi)似位置編碼”操作一樣將其進(jìn)行embedding處理然后在模型里面一般輸入的參數(shù)也就是這三部分：noise_image, time_step, class_label

Dit模型

將Transformer使用到Diffusion Model中，而Dit^[8]在論文中進(jìn)行的操作：通過(guò)一個(gè)autoencoder來(lái)將圖像壓縮為低維度的latent，擴(kuò)散模型用來(lái)生成latent，然后再采用autoencoder來(lái)重建出圖像，比如說(shuō)在Dit中使用KL-f8對(duì)于輸入圖像維度為：256x256x3那么壓縮得到的latent為32x32x4。Dit的模型結(jié)構(gòu)為：

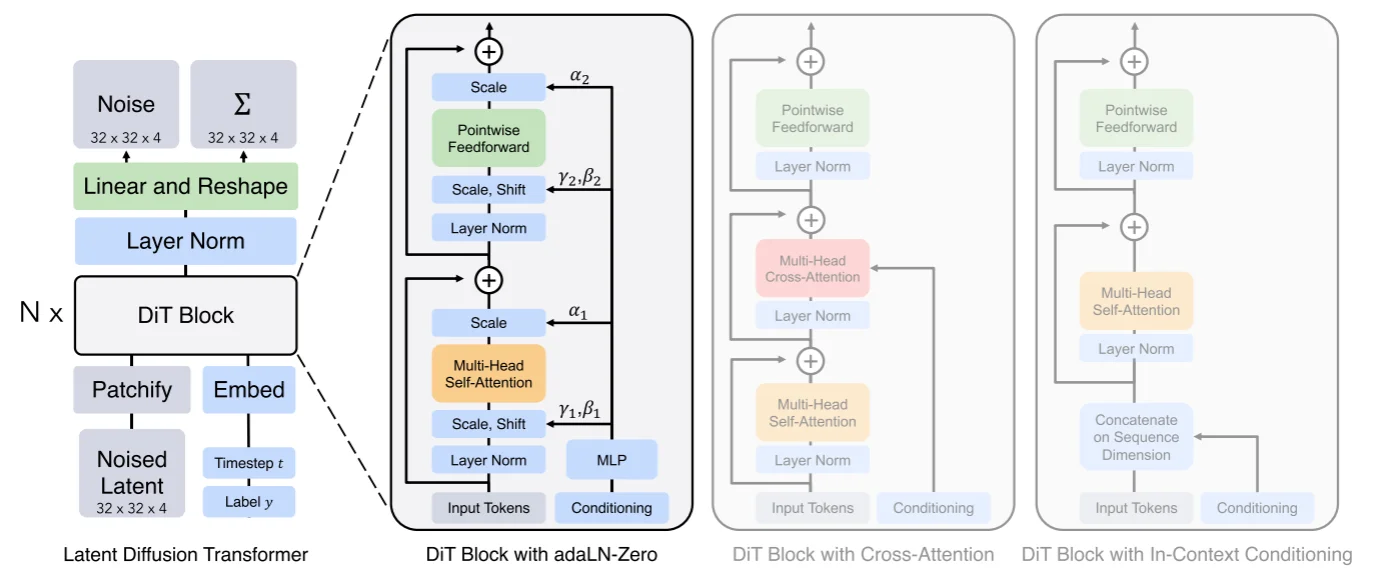
模型輸入?yún)?shù)3個(gè)分別為：1、低緯度的latent；2、標(biāo)簽label；3、時(shí)間步t。對(duì)于latent直接通過(guò)一個(gè)patch embed來(lái)得到不同的patch（得到一系列的token）而后將其和位置編碼進(jìn)行相加得到最后的embedding內(nèi)容，直接結(jié)合代碼^[9]來(lái)解釋模型：
假設(shè)模型的輸入為：

#Dit參數(shù)為：DiT(depth=12, hidden_size=384, patch_size=4, num_heads=6)
batch_size= 16
image = torch.randn(batch_size, 4, 32, 32).to(device)
t = torch.randint(0, 1000, (batch_size,)).to(device)
y = torch.randint(0, 1000, (batch_size,)).to(device)

那么對(duì)與輸入分別都進(jìn)行embedding處理：1、Latent Embedding：得到（8，64，384），因?yàn)閜atchembedding直接就是假設(shè)我們的patch size為4那么每個(gè)patch大小為：4x4x4=64并且得到32/4* 32/4=64個(gè)patches，而后通過(guò)線linear處理將64映射為hidden_size=384；2、Time Embedding和Label Embedding：得到（8，384）（8，384），因?yàn)閷?duì)于t直接通過(guò)sin進(jìn)行編碼，對(duì)于label在論文里面提到使用 classifier-free guidance方式，具體操作就是在訓(xùn)練過(guò)程中通過(guò)dropout_prob來(lái)將輸入標(biāo)簽隨機(jī)替換為無(wú)標(biāo)簽來(lái)生成無(wú)標(biāo)簽的向量，在 推理過(guò)程可以通過(guò) force_drop_ids來(lái)指定某些例子為無(wú)條件標(biāo)簽。將所有編碼后的內(nèi)容都通過(guò)補(bǔ)充位置編碼信息（latent embedding直接加全是1，而label直接加time embedding），補(bǔ)充完位置編碼之后就直接丟到 DitBlock中進(jìn)行處理，對(duì)于DitBlock結(jié)構(gòu)：

def forward(self, x, c):
    shift_msa, scale_msa, gate_msa, shift_mlp, scale_mlp, gate_mlp = self.adaLN_modulation(c).chunk(6, dim=1)
    x = x + gate_msa.unsqueeze(1) * self.attn(modulate(self.norm1(x), shift_msa, scale_msa))
    x = x + gate_mlp.unsqueeze(1) * self.mlp(modulate(self.norm2(x), shift_mlp, scale_mlp))
    return x

在這個(gè)代碼中不是直接使用注意力而是使用通過(guò)一個(gè) modulate這個(gè)為了實(shí)現(xiàn)將傳統(tǒng)的layer norm（\(\gamma{\frac{x- \mu}{\sigma}}+ \beta\)）改為動(dòng)態(tài)的\(\text{scale}{\frac{x- \mu}{\sigma}}+ \text{shift}\)，直接使用動(dòng)態(tài)是為了允許模型根據(jù)時(shí)間步和類(lèi)標(biāo)簽調(diào)整 Transformer 的行為，使生成過(guò)程更靈活和條件相關(guān)，除此之外將傳統(tǒng)的殘差連接改為 權(quán)重條件連接 \(x+cf(x)\)。再通過(guò)線性層進(jìn)行處理類(lèi)似的也是使用上面提到的正則化進(jìn)行處理，處理之后結(jié)果通過(guò)unpatchify處理（將channels擴(kuò)展2倍而后還原到最開(kāi)始的輸入狀態(tài)）

Unet模型結(jié)構(gòu)

Unet模型在前面有介紹過(guò)了就是通過(guò)下采樣和上采用并且同層級(jí)之間通過(guò)特征拼接來(lái)補(bǔ)齊不同采用過(guò)程之間的“信息”損失。如果直接使用stable diffusion model（封裝不多），假設(shè)參數(shù)如下進(jìn)行代碼操作：

{
    'ch': 64,
    'out_ch': 3,
    'ch_mult': (1, 2, 4), # 通道增加倍數(shù) in: 2,3,128,128 第一層卷積：2,64,128,128 通過(guò)這個(gè)參數(shù)直接結(jié)合 num_res_blocks來(lái)判斷通道數(shù)量增加 ch_mut*num_res_blocks=(1, 1, 2, 2, 4, 4)
    'num_res_blocks': 2,  # 殘差模塊數(shù)量
    'attn_resolutions': (16,),
    'dropout': 0.1,
    'resamp_with_conv': True,
    'in_channels': 3,
    'resolution': 128,
    'use_timestep': True,
    'use_linear_attn': False,
    'attn_type': "vanilla"
}

基本模塊

1、殘差模塊：

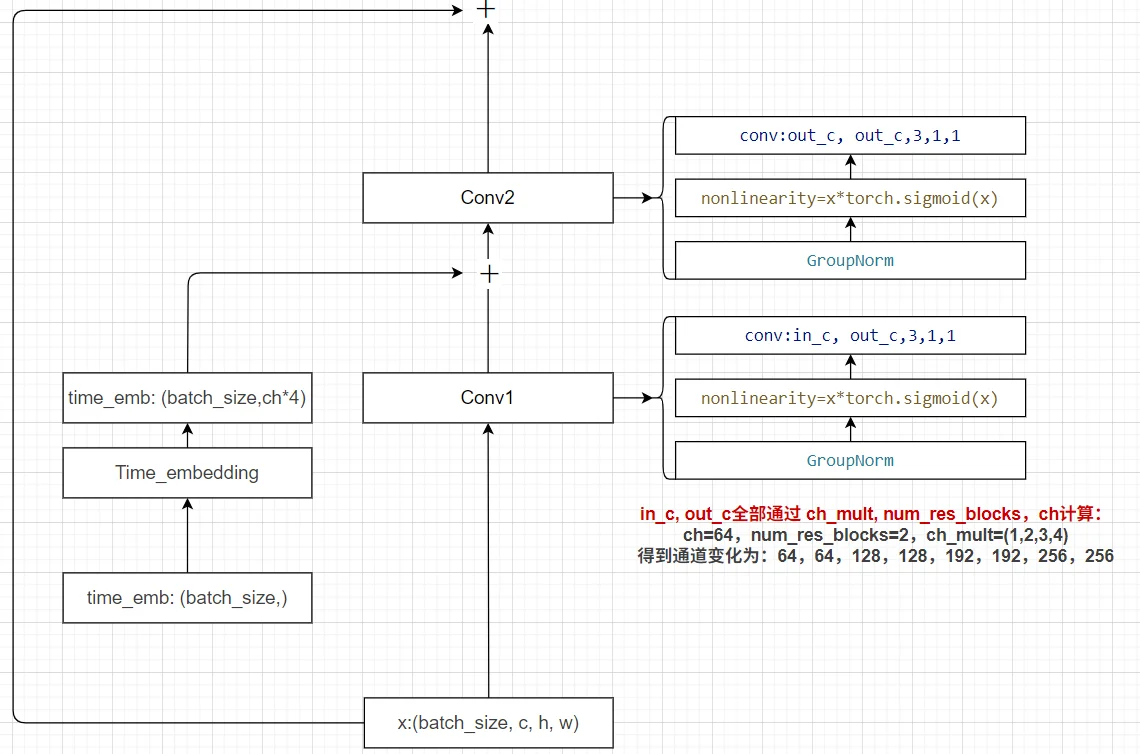
2、time embedding：直接使用attention的sin位置編碼

具體過(guò)程

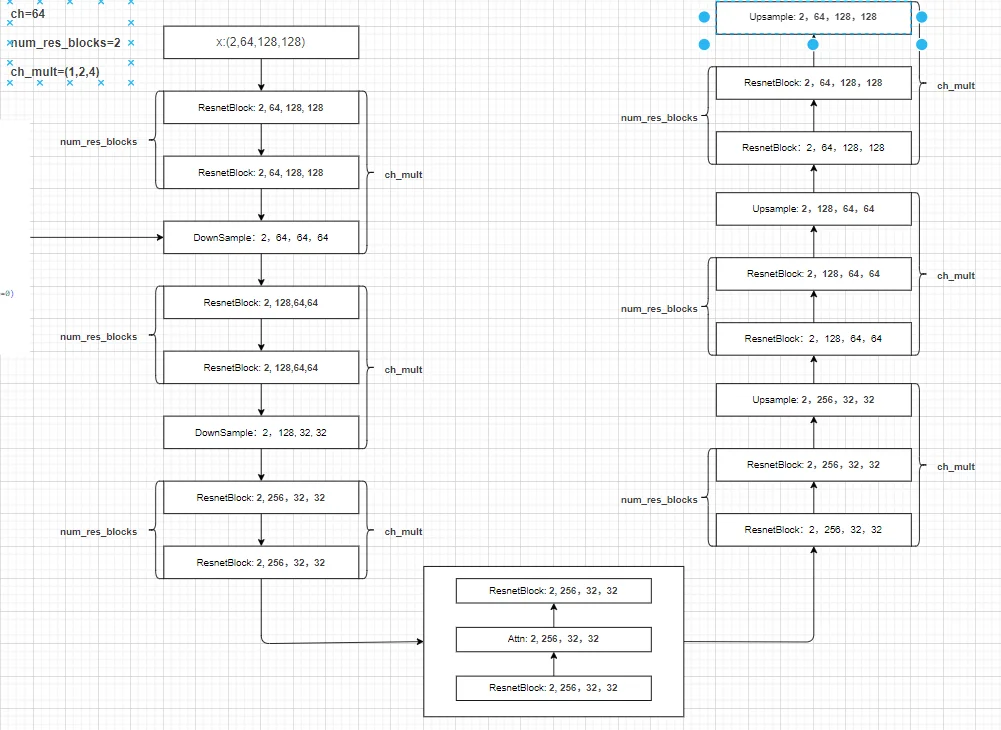
在得到的分辨率=attn_resolutions時(shí)候就會(huì)直接進(jìn)行注意力計(jì)算（直接用卷積處理得到q，k，v然后進(jìn)行計(jì)算attention），整個(gè)[結(jié)構(gòu)]({{ site.baseurl }}/Dio.drawio)。如果這里直接使用diffuser里面的UNet模型進(jìn)行解釋?zhuān)ㄊ褂肬Net2DModel模型解釋?zhuān)麄€(gè)Unet模型就是3部分：1、下采樣；2、中間層；3、上采樣。假設(shè)模型參數(shù)為：

model = UNet2DModel(
    sample_size= 128,
    in_channels=3,
    out_channels=3,
    layers_per_block=2,
    block_out_channels=(128, 128, 256, 256, 512, 512),
    down_block_types=("DownBlock2D", "DownBlock2D", "DownBlock2D", "DownBlock2D", "DownBlock2D", "DownBlock2D"),
    up_block_types=("UpBlock2D", "UpBlock2D", "UpBlock2D", "UpBlock2D", "UpBlock2D", "UpBlock2D")
).to(device)

整個(gè)過(guò)程維度變化，假設(shè)輸入為：image:(32,3,128,128), time_steps: (32, )：
首先通過(guò)第一層卷積：(32,128,128,128)與此同時(shí)會(huì)將時(shí)間步進(jìn)行編碼得到：(32, 512)（如果有l(wèi)abel數(shù)據(jù)也是(32,)那么會(huì)將其加入到time_steps中）
下采樣處理：總共6層下采樣，得到結(jié)果為：
Down-0: torch.Size([32, 128, 128, 128])
Down-1: torch.Size([32, 128, 64, 64])
Down-2: torch.Size([32, 256, 32, 32])
Down-3: torch.Size([32, 256, 16, 16])
Down-4: torch.Size([32, 512, 8, 8])
Down-5: torch.Size([32, 512, 4, 4])
中間層處理：torch.Size([32, 512, 4, 4])
上采樣處理：總共6層上采樣，得到結(jié)果為：
Up-0 torch.Size([32, 512, 8, 8])
Up-1 torch.Size([32, 512, 16, 16])
Up-2 torch.Size([32, 256, 32, 32])
Up-3 torch.Size([32, 256, 64, 64])
Up-4 torch.Size([32, 128, 128, 128])
Up-5 torch.Size([32, 128, 128, 128])
輸出：輸出就直接通過(guò)groupnorm以及silu激活之后直接通過(guò)一層卷積進(jìn)行處理得到：torch.Size([32, 128, 128, 128])

DF訓(xùn)練

生成具有隨機(jī)性展示圖像效果不能很好說(shuō)明模型生成能力

1、DDPM

對(duì)于傳統(tǒng)的DF訓(xùn)練（前向+反向）比較簡(jiǎn)單，直接通過(guò)輸入圖像而后不斷添加噪聲而后解噪。以huggingface^[10]上例子為例（測(cè)試代碼: Unet2Model.py），首先、對(duì)圖像進(jìn)行添加噪聲。而后、直接去對(duì)添加噪聲后的模型進(jìn)行訓(xùn)練“去噪”（也就是預(yù)測(cè)圖像中的噪聲）。最后、計(jì)算loss反向傳播。

對(duì)于加噪聲等過(guò)程可以直接借助 diffusers來(lái)進(jìn)行處理，對(duì)于diffuser：
1、schedulers：調(diào)度器
主要實(shí)現(xiàn)功能：1、圖片的前向過(guò)程添加噪聲（也就是上面的\(x_T=\sqrt{\bar{\alpha_T}}x_0+ \sqrt{1-\bar{\alpha_T}}\epsilon\)）；2、圖像的反向過(guò)程去噪；3、時(shí)間步管理等。如果不是用這個(gè)調(diào)度器也可以自己設(shè)計(jì)一個(gè)只需要：1、前向加噪過(guò)程（需要：使用固定的\(\beta\)還是變化的、加噪就比較簡(jiǎn)單直接進(jìn)行矩陣計(jì)算）；2、采樣策略

測(cè)試得到結(jié)果為（因?yàn)镠F官方提供了很好的參數(shù)去訓(xùn)練模型，因此測(cè)試新的數(shù)據(jù)集可能就沒(méi)有那么效果好，只是做一個(gè)效果展示調(diào)參可能可以改善模型最后生成效果）：

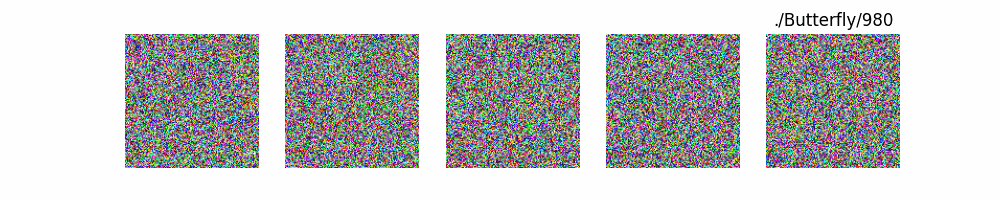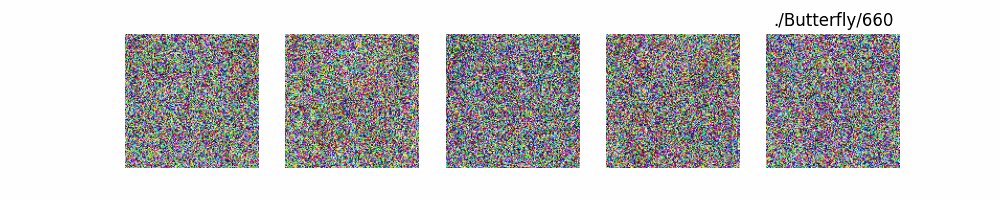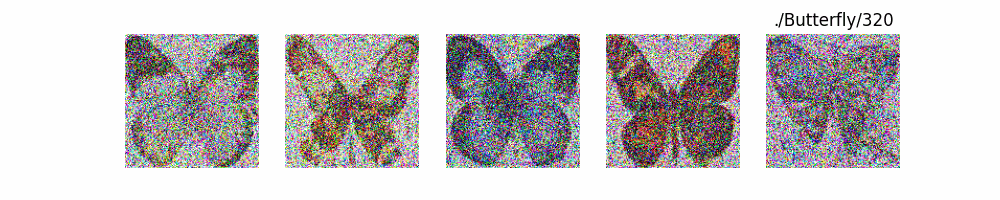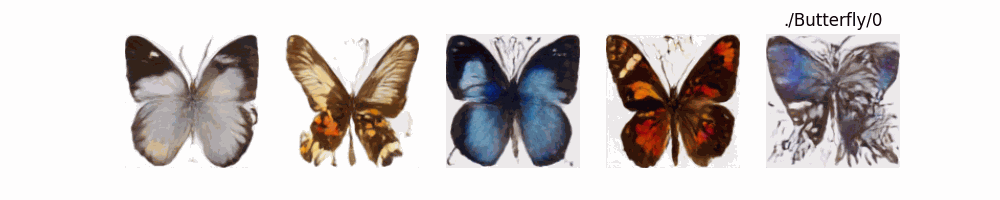
Stable Diffusion Model代碼測(cè)試。數(shù)據(jù)集："saitsharipov/CelebA-HQ"

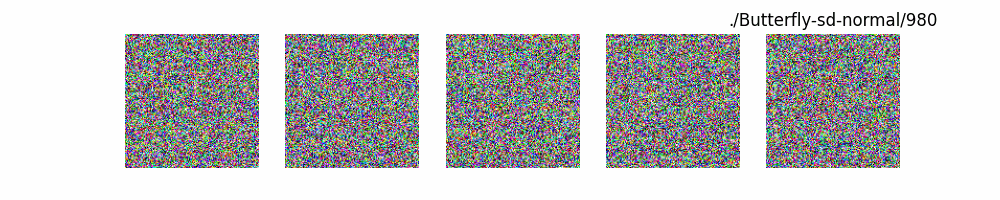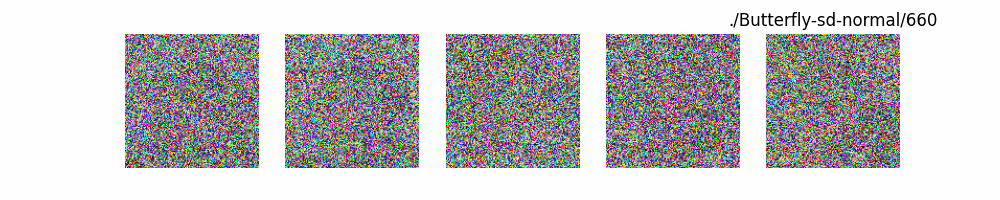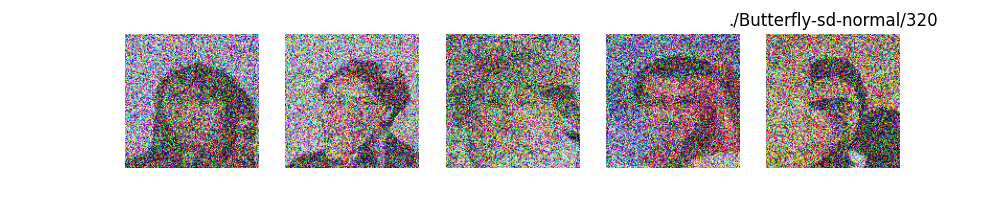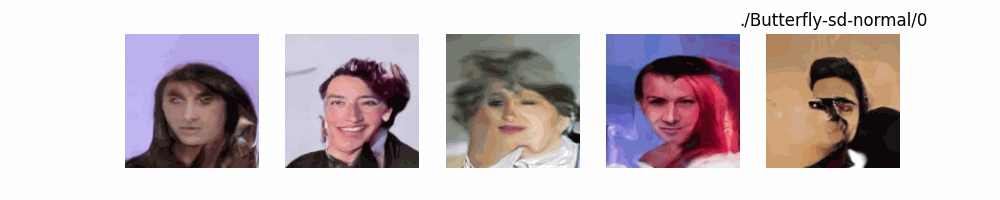
Hugging Face代碼測(cè)試。數(shù)據(jù)集："saitsharipov/CelebA-HQ"

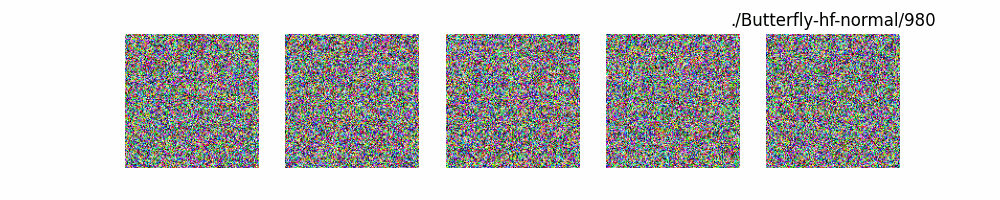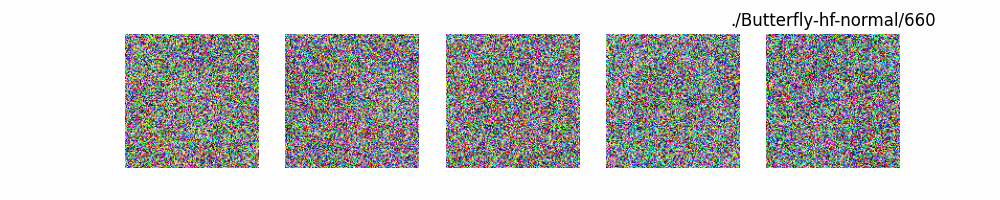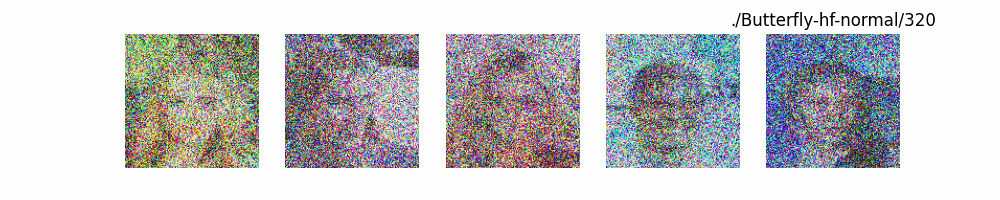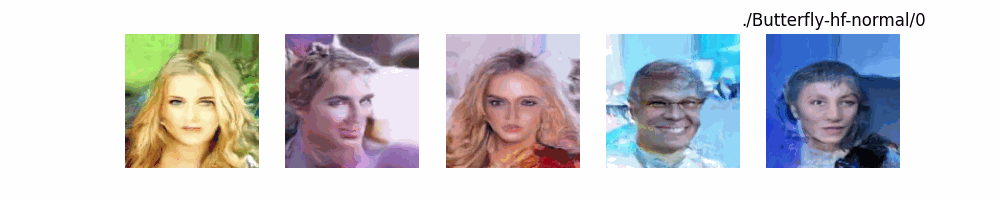
Dit代碼測(cè)試。數(shù)據(jù)集："saitsharipov/CelebA-HQ"

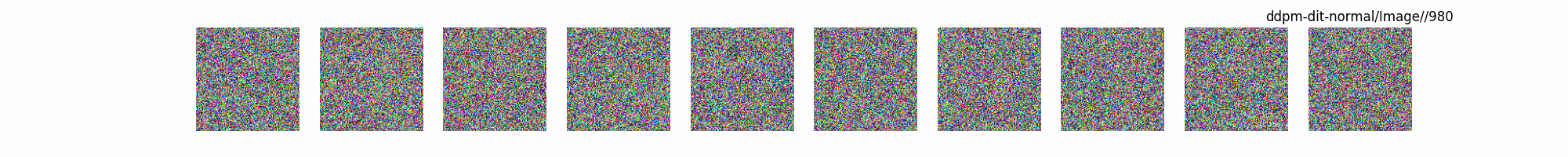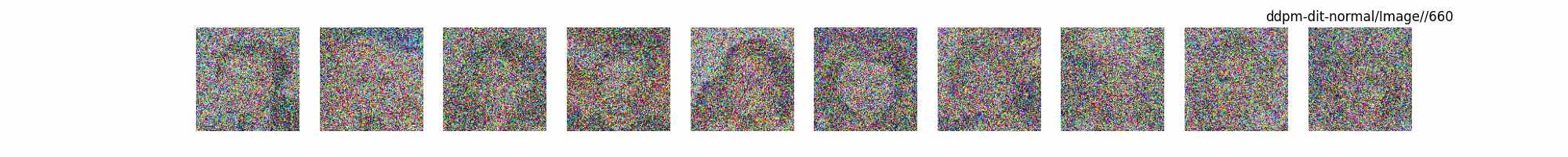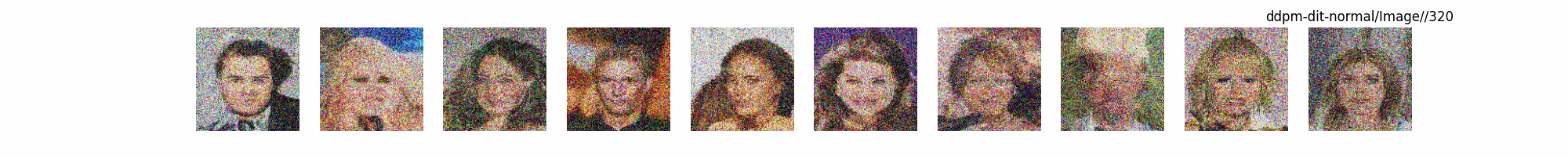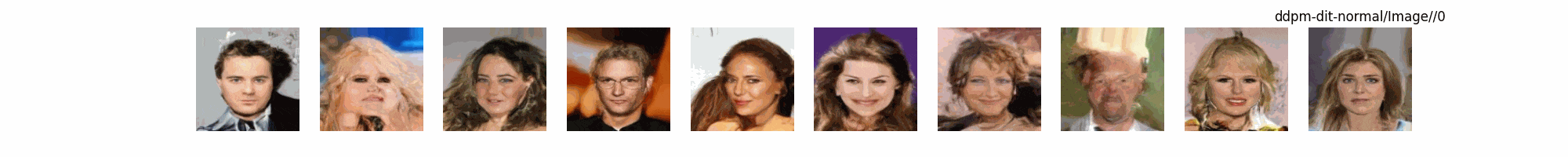
總結(jié)

上面介紹了各類(lèi)DF以及具體的代碼操作，總的來(lái)說(shuō)在DF訓(xùn)練過(guò)程中（從代碼角度）基本上就是這個(gè)公式：\(x_t=\sqrt{\bar{\alpha_t}}x_0+ \sqrt{1-\bar{\alpha_t}}\epsilon\) 加噪過(guò)程得到\(x_t\)/去噪過(guò)程通過(guò)\(x_t\)通過(guò)去預(yù)測(cè) 噪聲來(lái)優(yōu)化模型的參數(shù)。于此同時(shí)訓(xùn)練過(guò)程中發(fā)現(xiàn)：擴(kuò)散模型（如DDPM）確實(shí)傾向于先學(xué)習(xí)圖像的低頻信息（大致輪廓），再逐步學(xué)習(xí)高頻信息（細(xì)節(jié)），這是由于模型的去噪過(guò)程和損失函數(shù)設(shè)計(jì)，因此擴(kuò)散模型需要大量迭代（通常數(shù)千到數(shù)十萬(wàn)步）才能生成高質(zhì)量圖像，尤其在細(xì)節(jié)上需要長(zhǎng)時(shí)間優(yōu)化。比如下面為實(shí)際迭代過(guò)程中生成.

從左到右，從上到下，保存頻率為每20個(gè)epoch保存一次，使用的模型為dit模型

參考