如果?個機(jī)器學(xué)習(xí)模型運(yùn)?良好，為什么我們僅僅信任該模型?忽略為什么做出特定的決策呢？
諸如分類準(zhǔn)確性之類的單?指標(biāo)?法完整地描述?多數(shù)實(shí)際任務(wù)。當(dāng)涉及到預(yù)測模型時，需要作出權(quán)衡：你是只想知道預(yù)測是什么？例如，客戶流失的概率或某種藥物對病?的療效。還是想知道為什么做出這樣的預(yù)測？這種情況下可能為了可解釋性付出預(yù)測性能下降的代價。在某些情況下，你不必關(guān)?為什么要做出這樣的預(yù)測，只要知道模型在測試數(shù)據(jù)集的預(yù)測性能良好就?夠了。但是在其他情況下，了解 “為什么” 可以幫助你更多地了解問題、數(shù)據(jù)以及模型可能失敗的原因。有些模型可能不需要解釋，因?yàn)樗鼈兪窃诘惋L(fēng)險的環(huán)境中使?的，這意味著錯誤不會造成嚴(yán)重后果 (例如，電影推薦系統(tǒng))，或者該?法已經(jīng)被?泛研究和評估 (例如，光學(xué)字符識別 OCR)。對可解釋性的需求來?問題形式化的不完整性，這意味著對于某些問題或任務(wù)，僅僅獲得預(yù)測結(jié)果是不夠的。該模型還必須解釋是怎么獲得這個預(yù)測的，因?yàn)檎_的預(yù)測只部分地解決了你的原始問題。

機(jī)器學(xué)習(xí)可解釋性

需要建立一個解釋器來解釋黑盒模型，并且這個解釋器必須滿足以下特征：
可解釋性
要求解釋器的模型與特征都必須是可解釋的，像決策樹、線性模型都是很適合拿來解釋的模型；而可解釋的模型必須搭配可解釋的特征，才是真正的可解釋性，讓不了解機(jī)器學(xué)習(xí)的人也能通過解釋器理解模型。
局部保真度
既然我們已經(jīng)使用了可解釋的模型與特征，就不可能期望簡單的可解釋模型在效果上等同于復(fù)雜模型（比如原始CNN分類器）。所以解釋器不需要在全局上達(dá)到復(fù)雜模型的效果，但至少在局部上效果要很接近，而此處的局部代表我們想觀察的那個樣本的周圍。
與模型無關(guān)
這里所指的是與復(fù)雜模型無關(guān)，換句話說無論多復(fù)雜的模型，像是SVM或神經(jīng)網(wǎng)絡(luò)，該解釋器都可以工作。
除了傳統(tǒng)的特征重要性排序外，ICE、PDP、SDT、LIME、SHAP都是揭開機(jī)器學(xué)習(xí)模型黑箱的有力工具。

• 特征重要性計(jì)算依據(jù)某個特征進(jìn)行決策樹分裂時，分裂前后的信息增益（基尼系數(shù)）；
• ICE和PDP考察某項(xiàng)特征的不同取值對模型輸出值的影響；
• SDT用單棵決策樹解釋其它更復(fù)雜的機(jī)器學(xué)習(xí)模型；
• LIME的核心思想是對于每條樣本，尋找一個更容易解釋的代理模型解釋原模型；
• SHAP的概念源于博弈論，核心思想是計(jì)算特征對模型輸出的邊際貢獻(xiàn)；

1、機(jī)器學(xué)習(xí)可解釋性--LIME
2、機(jī)器學(xué)習(xí)可解釋性--SHAP

機(jī)器學(xué)習(xí)可解釋性--SHAP

1、Shapley Value

沙普利值^[1]（Shapley value），是通過考慮各個代理（agent）做出的貢獻(xiàn)，來公平地分配合作收益。代理的沙普利值是對于一個合作項(xiàng)目所期望的貢獻(xiàn)量的平均值。計(jì)算公式：
設(shè)\(I={1,2...n}\)為\(n\)個人的集合那么\(i\)的貢獻(xiàn)為：

其中\(S_{i}\)是\(I\)中包含成員\(i\)的所有子集形成的集合，\(w(|s|)\)是加權(quán)因子，\(s\i\)表示集合\(s\)中去掉元素\(i\)后的集合。
\(v(s)-v(s\i)\)成員i在聯(lián)盟中的貢獻(xiàn)，即成員i的邊際貢獻(xiàn)；\(w(|s|)\)權(quán)重\(w(|s|=\frac{(|s|-1)!(n-|s|)!}{n!})\)

WiKi：

玩家聯(lián)盟合作，并從合作中獲得一定的整體收益。由于一些參與者可能比其他參與者對聯(lián)盟貢獻(xiàn)更多，或者可能擁有不同的議價能力（例如威脅要摧毀全部盈余），因此在任何特定博弈中，參與者之間產(chǎn)生的盈余的最終分配應(yīng)該是什么？或者換句話說：每個參與者對整體合作有多重要，他或她可以合理預(yù)期的回報是什么？Shapley 值為這個問題提供了一個可能的答案。

1、https://en.wikipedia.org/wiki/Shapley_value
《可解釋的機(jī)器學(xué)習(xí)》
開源地址：
2、https://github.com/MingchaoZhu/InterpretableMLBook
在線閱讀：
3、https://hjezero.github.io/posts/32fedbdb/

借助《可解釋的機(jī)器學(xué)習(xí)》中例子，假設(shè)準(zhǔn)備購買一間公寓，其中你所感興趣的是：1、有無公園；2、公寓面積；3、公寓所位于的樓層；4、是否能養(yǎng)貓。而后對公寓價格預(yù)測。

?套 50 平??的公寓，附近有公園以及禁?貓?內(nèi)，預(yù)計(jì)價格為 300,000 歐元
那么1、公寓面積；2、公寓樓層；3、養(yǎng)貓？4、公園？這4個特征對預(yù)測價格300000歐元的貢獻(xiàn)是怎么樣的呢？
比如說^[2]：一個程序C=500行代碼需要編寫，今天產(chǎn)品經(jīng)理找了三個程序猿來完成，按照完成量發(fā)獎金：
條件一：\(V_{1}=100\)，\(V_{2}=125\)，\(V_{3}=50\)
解釋：1號屌絲程序猿獨(dú)立能寫100行，2號大神程序猿獨(dú)立能寫125行，3號美女程序猿能寫50行
條件二：\(V_{12}=270\)，\(V_{23}=350\)，\(V_{13}=375\)
解釋：1,2號合作能寫270行，2,3號合作能寫350行，1,3號合作能寫375行
條件三：\(V_{123}=500\)
3個人共同能完成500行
那么根據(jù)3組條件，合計(jì)6種組合分別如下：
A.1號程序猿邀請2號程序猿加入他組成S聯(lián)盟，1,2號邀請3號加入共同編寫。
B.1號邀請3號加入成為S小組，2號加入S小組
C.2號邀請1號加入成為S小組，3號加入S小組
D.2號邀請3號加入成為S小組，1號加入S小組
E.3號邀請1號加入成為S小組，2號加入S小組
F.3號邀請2號加入成為S小組，1號加入S小組
計(jì)算邊際貢獻(xiàn)：

根據(jù)公式1得到： 1的shapley value： $\frac{1}{6}(100+100+145+150+325+150)=\frac{970}{6}$

依次類推得到其他人的shapely value

2、A Unified Approach to Interpreting Model Predictions

SHAP Value與LIME的方法類似，都是通過定義簡單模型去對復(fù)雜模型進(jìn)行解釋。

“we must use a simpler explanation model, which we define as any interpretable approximation of the original model.” (Lundberg 和 Lee, 2017, p. 2)

我們必須使用一個更簡單的解釋模型，我們將其定義為對原模型的任何可解釋的近似。

回顧LIME模型，利用簡單函數(shù)\(g\)去在\(x\)“周圍”去對復(fù)雜函數(shù)\(f\)進(jìn)行局部近似。在本論文作者將部分解釋模型函數(shù)稱為Additive feature attribution methods其形式形如：

其中：\(M\)所有的簡單輸入特征的個數(shù)；\(\phi_{i}\)每一種特征的貢獻(xiàn)（對于的shapely值）；通過計(jì)算所有特征的貢獻(xiàn)去近似復(fù)雜函數(shù)\(f(x)\)

論文中部分解釋模型函數(shù)有：

1、LIME模型對貢獻(xiàn)計(jì)算：

\[\xi(s)= argmin_{g\in G} L(f,g,\pi_{x})+\Omega(g) \]

2、DeepLIFT（面向深度學(xué)習(xí)的可解釋方法）模型對貢獻(xiàn)計(jì)算：

\[\sum_{i=1}^{n}C_{\Delta x_{i}\Delta o}=\Delta o \]

貢獻(xiàn)為：\(C_{\Delta x_{i}\Delta o}\)，其中\(o=f(x)\)為模型的輸出，其中\(r\)為參考的樣本輸入，\(\Delta o=f(x)-f(r)\)。
3、經(jīng)典Shapley Value計(jì)算：

• Shapley regression values

feature importances for linear models in the presence of multicollinearity.
此模型要求計(jì)算模型所有的特征，認(rèn)為每一個特征在模型中都起到了作用。計(jì)算公式如下：

> 就是上面列子中提及到的計(jì)算方法 * Shapley sampling values * Quantitative Input Influence

對于additive feature attribution methods存在如下三點(diǎn)性質(zhì)：
1、Local accuracy
2、Missingness
3、Consistency

Kernel SHAP(Linear LIME + Shapley values)

Kernel SHAP計(jì)算步驟：

※1. 初始化一些數(shù)據(jù), z', 作為Simplified Features（隨機(jī)生成（0,1,1,0）,(1,0,1,1)等）

其中：\(z'_{k}\in{(0,1)}^{M}\)（0：缺失特征；1：初始化中存在的特征）其中\(M\)是我們的維數(shù)（理解為樣本特征數(shù)目），\(k\in{(1,...K)}\)代表生成數(shù)據(jù)個數(shù)

※2. 將上面的Simplified Features轉(zhuǎn)換到原始數(shù)據(jù)空間, 并計(jì)算對應(yīng)的預(yù)測值, f(h(z'))

比如說上面賣房子例子，有四個特征所以\(M=4\)那么假設(shè)初始化為\(z'_{1}=(0,1,1,0)\)那么也就是存在第二和第三個特征的聯(lián)盟，那么對于第一個和第四個則通過\(h\)函數(shù)進(jìn)行轉(zhuǎn)換

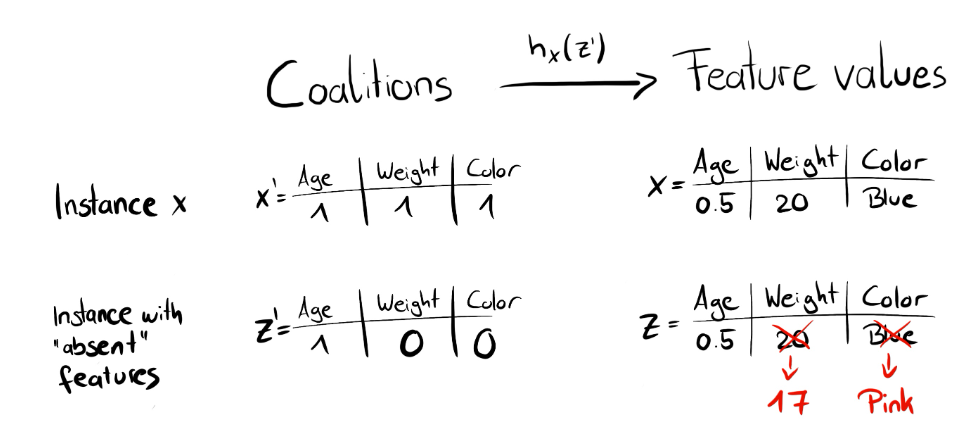
※3. 對每一個z'計(jì)算對應(yīng)的權(quán)重

Kernel SHAP的權(quán)重函數(shù)\(\pi\)為：\(\pi_{x^{'}}(z^{'})=\frac{M-1}{(M\;choose\;|z^{'}|)(M-|z^{'}|)}\)，其中\(M\)為維數(shù)（所有特征的個數(shù)），\(|z^{'}|\)代表樣本中1的個數(shù)，\(M\;choose\;|z^{'}|\)代表\(C_{M}^{z^{'}}|z^{'}|\)。容易得到：若有很多1或很多0則取較高的權(quán)重，若0和1數(shù)量相近則取較低的權(quán)重。

LIME則是通過距離設(shè)置權(quán)重

※4. 擬合線性模型
※5. 計(jì)算出每一個特征的Shapley Value, 也就是線性模型的系數(shù)

Kernel SHAP計(jì)算

損失函數(shù)：

代碼

參考

1、https://github.com/MingchaoZhu/InterpretableMLBook

2、https://www.zhihu.com/question/23180647

3、[關(guān)于Shapley Value（夏普利值）的公式 - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/483891565#:~:text=Shapley Value公式如下： 記 I%3D { 1%2C2%2C...%2Cn}為n個合作人的集合 varphi_i (upsilon),- upsilon (s backslash { i })]})

4、https://e0hyl.github.io/BLOG-OF-E0/LIMEandSHAP/

5、https://mathpretty.com/10699.html

推薦閱讀

1、https://christophm.github.io/interpretable-ml-book